Representing Linear Transformations by Matrices

Let $f: V \rightarrow W$ be a linear transformation of finite dimensional vector spaces. Choose ordered bases ${\cal B} = \{v_1, \ldots, v_n\}$ for V and ${\cal C} = \{w_1, \ldots, w_m\}$ for W.

For each j, $f(v_j) \in W$ . Therefore, $f(v_j)$ may be written uniquely as a linear combination of elements of ${\cal C}$ :

$$f(v_j) = \sum_{i=0}^m a_{ij} w_i.$$

The numbers $\{ a_{ij}\}$ are uniquely determined by f. The $m \times n$ matrix $A = (a_{ij})$ is the matrix of f relative to the ordered bases ${\cal B}$ and ${\cal C}$ . I'll use $[f]_{{\cal B},{\cal C}}$ to denote this matrix. Here's how to find it.

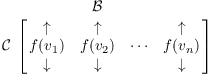
$$\bordermatrix{& & {\cal B} & & \cr & \uparrow & \uparrow & & \uparrow \cr {\cal C} & f(v_1) & f(v_2) & \cdots & f(v_n) \cr & \downarrow & \downarrow & & \downarrow \cr}$$

I'll use std to denote the standard basis for $F^n$ .

Example. Here are two bases for $\real^2$ :

$${\cal B} = \left\{\left[\matrix{1 \cr 3 \cr}\right], \left[\matrix{1 \cr 2 \cr}\right]\right\},$$

$${\cal C} = \left\{\left[\matrix{1 \cr 1 \cr}\right], \left[\matrix{1 \cr -1 \cr}\right]\right\}.$$

Suppose $f: \real^2 \to \real^2$ is a linear transformation such that

$$f\left[\matrix{1 \cr 3 \cr}\right] = 6\cdot \left[\matrix{1 \cr 1 \cr}\right] + 11\cdot \left[\matrix{1 \cr -1 \cr}\right] \quad\hbox{and}\quad f\left[\matrix{1 \cr 2 \cr}\right] = (-13)\cdot \left[\matrix{1 \cr 1 \cr}\right] + \pi\cdot \left[\matrix{1 \cr -1 \cr}\right].$$

Then

$$[f]_{{\cal B}, {\cal C}} = \left[\matrix{6 & -13 \cr 11 & \pi \cr}\right].$$

Read the description of $[f]_{{\cal B}, {\cal C}}$ preceding this example and verify that $[f]_{{\cal B}, {\cal C}}$ was constructed by following the steps in the description.

Example. (a) Define $f: \real^2 \to \real^3$ by

$$f(x,y) = (x + 2y, 3x, -x + 5y).$$

Find $[f]_{{\rm std}, {\rm std}}$ .

Apply f to the elements of the standard basis for $\real^2$ , and write the results in terms of the standard basis for $\real^3$ :

$$f(1,0) = (1,3,-1) = 1\cdot (1,0,0) + 3\cdot (0,1,0) + (-1)\cdot (0,0,1),$$

$$f(0,1) = (2,0,5) = 2\cdot (1,0,0) + 0\cdot (0,1,0) + 5\cdot (0,0,1).$$

Take the coefficients in the linear combinations and use them to make the columns of the matrix:

$$[f]_{{\rm std}, {\rm std}} = \left[\matrix{1 & 2 \cr 3 & 0 \cr -1 & 5 \cr}\right].$$

Note that in matrix form,

$$f\left(\left[\matrix{x \cr y \cr}\right]\right) = \left[\matrix{1 & 2 \cr 3 & 0 \cr -1 & 5 \cr}\right] \left[\matrix{x \cr y \cr}\right].$$

In other words, $[f]_{std, std}$ is the same matrix as the one you'd usually use to represent f by matrix multiplication.

(b) Let ${\cal B} = \{(3, 1), (2, 1)\}$ . Define $f: \real^2 \to \real^2$ by

$$f(x,y) = (2 x - y, 5 x + y).$$

Find $[f]_{{\rm std}, {\cal B}}$ .

Apply f to the elements of the standard basis for $\real^2$ , and write the results in terms of ${\cal B}$ :

$$f(1, 0) = (2, 5) = (-8) \cdot (3, 1) + 13 \cdot (2, 1),$$

$$f(0, 1) = (-1, 1) = (-3) \cdot (3, 1) + 4 \cdot (2, 1).$$

Take the coefficients in the linear combinations and use them to make the columns of the matrix:

$$[f]_{{\rm std}, {\cal B}} = \left[\matrix{-8 & -3 \cr 13 & 4 \cr}\right].\quad\halmos$$

Here is a description of $[f]_{{\cal B}, {\cal C}}$ in words:

If you keep this in mind, change of coordinates will make much more sense.

I'll verify the claim above for one of the basis elements $v_j$ . In terms of ${\cal B}$ ,

$$\matrix{v_j = & (0, & \ldots, & 0, & 1, & 0, & \ldots, & 0). \cr & & & & {\scriptstyle j} & & & \cr}$$

Then

$$\left[\matrix{ a_{11} & \cdots & a_{1j} & \cdots & a_{1n} \cr a_{21} & \cdots & a_{2j} & \cdots & a_{2n} \cr \vdots & & \vdots & & \vdots \cr a_{m1} & \cdots & a_{mj} & \cdots & a_{mn} \cr}\right] \left[\matrix{ 0 \cr \vdots \cr 1 \cr \vdots \cr 0 \cr}\right] = \left[\matrix{ a_{1j} \cr a_{2j} \cr \vdots \cr a_{mj} \cr}\right].$$

This is correct, since $\displaystyle f(v_j) = \sum_{i=0}^m a_{ij} w_i$ , and the representation of $\displaystyle \sum_{i=0}^m a_{ij} w_i$ in terms of the basis ${\cal C} = \{ w_1, \ldots, w_m\}$ is

$$(a_{1j}, a_{2j}, \ldots, a_{mj}).$$

The matrix of a linear transformation is like a snapshot of a person --- there are many pictures of a person, but only one person. Likewise, a given linear transformation can be represented by matrices with respect to many choices of bases for the domain and range.

In the last example, finding $[f]_{{\rm std}, {\rm std}}$ turned out to be easy, whereas finding the matrix of f relative to other bases is more difficult. Here's how to use change of basis matrices to make things simpler.

Suppose you have bases ${\cal B}$ and ${\cal C}$ and you want $[f]_{{\cal B}, {\cal C}}$ .

1. Find $[f]_{{\rm std}, {\rm std}}$ . Usually, you can find this from the definition.

2. Find the change of basis matrices $[{\cal B} \to {\rm std}]$ and $[{\cal C} \to {\rm std}]$ . (Take the basis elements written in terms of the standard bases and use them as the columns of the matrices.)

3. Find $[{\rm std} \to {\cal C}] = [{\cal C} \to {\rm std}]^{-1}$ .

4. Then

$$[f]_{{\cal B}, {\cal C}} = [{\rm std} \to {\cal C}][f]_{{\rm std}, {\rm std}} [{\cal B} \to {\rm std}].$$

Do you see why this works? Reading from right to left, an input vector written in terms of ${\cal B}$ is translated to the standard basis by $[{\cal B} \to {\rm std}]$ . Next, $[f]_{{\rm std}, {\rm std}}$ takes the standard vector, applies f, and writes the output as a standard vector. Finally, $[{\rm std} \to {\cal C}]$ takes the standard vector output and translates it to a ${\cal C}$ vector.

I'll illustrate this in the next example.

Example. Define $f: \real^2 \rightarrow \real^3$ by

$$f\left[\matrix{x \cr y \cr}\right] = \left[\matrix{x + y \cr 2x - y \cr x - y \cr}\right] = \left[\matrix{1 & 1 \cr 2 & -1 \cr 1 & -1 \cr}\right] \left[\matrix{x \cr y \cr}\right].$$

The matrix above is the matrix of f relative to the standard bases of $\real^2$ and $\real^3$ .

Next, consider the following bases for $\real^2$ and $\real^3$ , respectively:

$${\cal B} = \left\{\left[\matrix{2 \cr 1 \cr}\right], \left[\matrix{1 \cr 1 \cr}\right]\right\},$$

$${\cal C} = \left\{\left[\matrix{1 \cr 1 \cr 1\cr}\right], \left[\matrix{1 \cr 2 \cr 1 \cr}\right], \left[\matrix{-1 \cr 0 \cr -2 \cr}\right]\right\}.$$

I'll find the matrix $[f]_{{\cal B},{\cal C}}$ of f relative to ${\cal B}$ and ${\cal C}$ . Here's how:

$$[f]_{{\cal B},{\cal C}} = [{\rm std} \to {\cal C}][f]_{{\rm std}, {\rm std}} [{\cal B} \to {\rm std}].$$

This matrix translates vectors in $\real^2$ from ${\cal B}$ to the standard basis:

$$[{\cal B} \to {\rm std}] = \left[\matrix{ 2 & 1 \cr 1 & 1 \cr}\right].$$

This matrix translates vectors in $\real^3$ from ${\cal C}$ to the standard basis:

$$[{\cal C} \to {\rm std}] = \left[\matrix{ 1 & 1 & -1 \cr 1 & 2 & 0 \cr 1 & 1 & -2 }\right].$$

Hence, the inverse matrix translates vectors from the standard basis to ${\cal C}$ :

$$[{\rm std} \to {\cal C}] = \left[\matrix{ 1 & 1 & -1 \cr 1 & 2 & 0 \cr 1 & 1 & -2 }\right]^{-1} = \left[\matrix{ 4 & -1 & -2 \cr -2 & 1 & 1 \cr 1 & 0 & -1 \cr}\right].$$

Therefore,

$$[f]_{{\cal B},{\cal C}} = \left[\matrix{ 4 & -1 & -2 \cr -2 & 1 & 1 \cr 1 & 0 & -1 \cr}\right] \left[\matrix{ 1 & 1 \cr 2 & -1 \cr 1 & -1 \cr}\right] \left[\matrix{ 2 & 1 \cr 1 & 1 \cr}\right] = \left[\matrix{ 7 & 7 \cr -2 & -3 \cr 2 & 2 \cr}\right].\quad\halmos$$

Example. (a) Suppose $T: \real^2 \to \real^2$ satisfies

$$T\left(\left[\matrix{1 \cr 0 \cr}\right]\right) = \left[\matrix{1 \cr 1 \cr}\right] \quad\hbox{and}\quad T\left(\left[\matrix{0 \cr 1 \cr}\right]\right) = \left[\matrix{1 \cr -1 \cr}\right].$$

What is $T\left(\left[\matrix{3 \cr -5 \cr}\right]\right)$ ?

Write $(3,-5)$ as a linear combination of $( 1,0)$ and $(0,1)$ :

$$\left[\matrix{3 \cr -5 \cr}\right] = 3\cdot \left[\matrix{1 \cr 0 \cr}\right] + (-5)\cdot \left[\matrix{0 \cr 1 \cr}\right].$$

The numbers are simple enough that I could figure out the linear combination by inspection.

Apply T:

$$T\left(\left[\matrix{3 \cr -5 \cr}\right]\right) = T\left(3\cdot \left[\matrix{1 \cr 0 \cr}\right] + (-5)\cdot \left[\matrix{0 \cr 1 \cr}\right]\right) = 3\cdot T\left(\left[\matrix{1 \cr 0 \cr}\right]\right) + (-5)\cdot T\left(\left[\matrix{0 \cr 1 \cr}\right]\right) =$$

$$3\cdot \left[\matrix{1 \cr 1 \cr}\right] + (-5)\cdot \left[\matrix{1 \cr -1 \cr}\right] = \left[\matrix{3 \cr 3 \cr}\right] + \left[\matrix{-5 \cr 5 \cr}\right] = \left[\matrix{-2 \cr 8 \cr}\right].\quad\halmos$$

(b) ${\cal B} = \{(1,1), (1,-1)\}$ is a basis for $\real^2$ . Suppose $T: \real^2 \to \real^2$ satisfies

$$T\left(\left[\matrix{1 \cr 1 \cr}\right]\right) = \left[\matrix{2 \cr -1 \cr}\right] \quad\hbox{and}\quad T\left(\left[\matrix{1 \cr -1 \cr}\right]\right) = \left[\matrix{1 \cr 2 \cr}\right].$$

What is $T\left(\left[\matrix{3 \cr -5 \cr}\right]\right)$ ?

Consider the equations for T above. T is applied to the elements of ${\cal B}$ , and the results are written in terms of the standard basis. Thus,

$$[T]_{{\cal B}, {\rm std}} = \left[\matrix{2 & 1 \cr -1 & 2 \cr}\right].$$

Since I'm applying T to the standard vector $(3,-5)$ , I have to translate this to a ${\cal B}$ vector to use the T-matrix I found.

$$[{\cal B} \to {\rm std}] = \left[\matrix{1 & 1 \cr 1 & -1 \cr}\right], \quad\hbox{so}\quad [{\rm std} \to {\cal B}] = \left[\matrix{1 & 1 \cr 1 & -1 \cr}\right]^{-1} = \dfrac{1}{2}\left[\matrix{1 & 1 \cr 1 & -1 \cr}\right].$$

Therefore,

$$\left[\matrix{3 \cr -5 \cr}\right] = \dfrac{1}{2}\left[\matrix{1 & 1 \cr 1 & -1 \cr}\right] \left[\matrix{3 \cr -5 \cr}\right] = \left[\matrix{-1 \cr 4 \cr}\right]_{\cal B}.$$

Hence,

$$T\left(\left[\matrix{3 \cr -5 \cr}\right]\right) = \left[\matrix{2 & 1 \cr -1 & 2 \cr}\right] \left[\matrix{-1 \cr 4 \cr}\right]_{\cal B} = \left[\matrix{2 \cr 9 \cr}\right].\quad\halmos$$

Example. Suppose $T: \real^2 \to \real^2$ is given by

$$T(x,y) = (4x - 2y, x + y).$$

Let

$${\cal B} = \left\{\left[\matrix{5 \cr 3 \cr}\right], \left[\matrix{1 \cr 1 \cr}\right]\right\}.$$

(a) Find $[T]_{{\rm std},{\rm std}}$ .

$$[T]_{{\rm std},{\rm std}} = \left[\matrix{4 & -2 \cr 1 & 1 \cr}\right].\quad\halmos$$

(b) Find $[T]_{{\cal B}, {\cal B}}$ .

First,

$$[{\cal B} \to {\rm std}] = \left[\matrix{5 & 1 \cr 3 & 1 \cr}\right].$$

Hence,

$$[{\rm std} \to {\cal B}] = [{\cal B} \to {\rm std}]^{-1} = \left[\matrix{5 & 1 \cr 3 & 1 \cr}\right]^{-1} = \dfrac{1}{2} \left[\matrix{1 & -1 \cr -3 & 5 \cr}\right].$$

Then

$$[T]_{{\cal B}, {\cal B}} = [{\rm std} \to {\cal B}] [T]_{{\rm std},{\rm std}} [{\cal B} \to {\rm std}] = \dfrac{1}{2} \left[\matrix{1 & -1 \cr -3 & 5 \cr}\right] \left[\matrix{4 & -2 \cr 1 & 1 \cr}\right] \left[\matrix{5 & 1 \cr 3 & 1 \cr}\right] = \left[\matrix{3 & 0 \cr -1 & 2 \cr}\right].\quad\halmos$$

(c) Compute $[T((4,3)_{\cal B})]_{\cal B}$ .

This means: Apply T to the vector $(4,3)_{\cal B}$ and write the result in terms of ${\cal B}$ .

$$[T((4,3)_{\cal B})]_{\cal B} = [T]_{{\cal B}, {\cal B}}\cdot (4,3)_{\cal B} = \left[\matrix{3 & 0 \cr -1 & 2 \cr}\right] \left[\matrix{4 \cr 3 \cr}\right] = \left[\matrix{12 \cr 2 \cr}\right]_{\cal B}.\quad\halmos$$

Example. Here are two bases for $\real^2$ :

$${\cal B} = \left\{\left[\matrix{1 \cr 1 \cr}\right], \left[\matrix{1 \cr -1 \cr}\right]\right\} \quad\hbox{and}\quad {\cal C} = \left\{\left[\matrix{3 \cr 1 \cr}\right], \left[\matrix{2 \cr 1 \cr}\right]\right\}.$$

Suppose $T: \real^2 \to \real^2$ is defined by

$$T\left(\left[\matrix{1 \cr 1 \cr}\right]\right) = 3\cdot \left[\matrix{3 \cr 1 \cr}\right] + (-4)\cdot \left[\matrix{2 \cr 1 \cr}\right] \quad\hbox{and}\quad T\left(\left[\matrix{1 \cr -1 \cr}\right]\right) = (-2)\cdot \left[\matrix{3 \cr 1 \cr}\right] + 3\cdot \left[\matrix{2 \cr 1 \cr}\right].$$

(a) Find $[T]_{{\cal B},{\cal C}}$ .

$$T\left(\left[\matrix{1 \cr 1 \cr}\right]\right) = (3,-4)_{\cal C} \quad\hbox{and}\quad T\left(\left[\matrix{1 \cr -1 \cr}\right]\right) = (-2,3).$$

Make a matrix using these coordinate vectors as the columns:

$$[T]_{{\cal B},{\cal C}} = \left[\matrix{3 & -2 \cr -4 & 3 \cr}\right].\quad\halmos$$

(b) Find $[T]_{{\rm std},{\rm std}}$ .

$$[T]_{{\rm std},{\rm std}} = [{\cal C} \to {\rm std}][T]_{{\cal B},{\cal C}} [{\rm std} \to {\cal B}].$$

Find the translation matrices:

$$[{\cal C} \to {\rm std}] = \left[\matrix{3 & 2 \cr 1 & 1 \cr}\right],$$

$$[{\cal B} \to {\rm std}] = \left[\matrix{1 & 1 \cr 1 & -1 \cr}\right], \quad\hbox{so}\quad [{\rm std} \to {\cal B}] = \left[\matrix{1 & 1 \cr 1 & -1 \cr}\right]^{-1} = \dfrac{1}{2}\left[\matrix{1 & 1 \cr 1 & -1 \cr}\right].$$

Therefore,

$$[T]_{{\rm std},{\rm std}} = \left[\matrix{3 & 2 \cr 1 & 1 \cr}\right]\cdot \left[\matrix{3 & -2 \cr -4 & 3 \cr}\right]\cdot \dfrac{1}{2}\left[\matrix{1 & 1 \cr 1 & -1 \cr}\right] = \dfrac{1}{2}\left[\matrix{1 & 1 \cr 0 & -2 \cr}\right].\quad\halmos$$

Send comments about this page to: Bruce.Ikenaga@millersville.edu.

Bruce Ikenaga's Home Page

Copyright 2012 by Bruce Ikenaga