Binary Operations

Definition. A binary operation on a set X is a function $f: X \times X \to X$ .

In other words, a binary operation takes a pair of elements of X and produces an element of X.

It's customary to use infix notation for binary operations. Thus, rather than write for the binary operation acting on elements $a, b \in X$ , you write . Since all those letters can get confusing, it's also customary to use certain symbols --- +, $\cdot$ , $\ast$ --- for binary operations. Thus, becomes (say) or $a\cdot b$ or $a \ast b$ .

Example. Addition is a binary operation on the set $\integer$ of integers: For every pair of integers m, n, there corresponds an integer .

Multiplication is also a binary operation on the set $\integer$ of integers: For every pair of integers m, n, there corresponds an integer $m \cdot n$ .

However, division is not a binary operation on the set $\integer$ of integers. For example, if I take the pair , I can't perform the operation $\dfrac{3}{0}$ . A binary operation on a set must be defined for all pairs of elements from the set.

Likewise,

$a \ast b = (\hbox{a random number bigger than a or b})$

does not define a binary operation on $\integer$ . In this case, I don't have a function $\integer \times \integer \to \integer$ , since the output is ambiguously defined. (Is $3 \ast 5$ equal to 6? Or is it 117?)

When a binary operation occurs in mathematics, it usually has properties that make it useful in constructing abstract structures.

Definition. Let $\ast$ be a binary operation on a set X.

$\ast$ is associative if

$x \ast (y \ast z) = (x \ast y) \ast z \quad\hbox{for all}\quad x, y, z \in X.$

$\ast$ is commutative if

$x \ast y = y \ast x \quad\hbox{for all}\quad x, y \in X.$

$e \in X$ is an identity for $\ast$ if

$e \ast x = x \quad\hbox{and}\quad x \ast e = x \quad\hbox{for all}\quad x \in X.$

If $\ast$ has an identity and $x \in X$ , then $x^{-1}$ is an inverse for x if

$x^{-1} \ast x = e \quad\hbox{and}\quad x \ast x^{-1} = e.$

For instance, in abstract algebra you will learn about groups. A group is a set G with a binary operation which is associative, has an identity element, and such that every element has an inverse.

Example. Addition is a binary operation on $\real$ .

It is associative, since

$a + (b + c) = (a + b) + c \quad\hbox{for all}\quad a, b, c \in \real.$

It is commutative, since

$a\cdot b = b\cdot a \quad\hbox{for all}\quad a, b \in \real.$

0 is an identity for +, since

$a + 0 = a \quad\hbox{and}\quad 0 + a = a \quad\hbox{for all}\quad a \in \real.$

If $a \in \real$ , then is an inverse for a with respect to addition:

$a + (-a) = 0 \quad\hbox{and}\quad (-a) + a = 0 \quad\hbox{for all}\quad a \in \real.\quad\halmos$

Example. Subtraction is a binary operation on $\real$ .

It is not associative; for example,

$3 - (4 - 5) = 3 - (-1) = 4, \quad\hbox{but}\quad (3 - 4) - 5 = -1 - 5 = -6.$

It is not commutative; for example,

$2 - 7 = -5, \quad\hbox{but}\quad 7 - 2 = 5.$

There is no identity element for subtraction. Suppose that e was an identity element. Then

$e - 2 = 2, \quad\hbox{so}\quad e = 4.$

But I'd also have

$e - 13 = 13, \quad\hbox{so}\quad e = 26.$

e can't be both 4 and 26, so this contradiction shows that there is no such e.

Since there is no identity element, it makes no sense to ask whether there are inverses.

Example. Consider the binary operation $\ast$ on $\real$ given by

$x \ast y = x + y - 3.$

$(x \ast y) \ast z = (x + y - 3) \ast z = (x + y - 3) + z - 3 = x + y + z - 6,$

$x \ast (y \ast z) = x \ast (y + z - 3) = x + (y + z - 3) - 3 = x + y + z - 6.$

Therefore, $\ast$ is associative.

Since

$x \ast y = x + y - 3 = y + x - 3 = y \ast x,$

$\ast$ is commutative.

To see if $\ast$ has an identity, I'll work backwards to guess a possible identity. Then I'll check that my guess works.

Suppose e is the identity. Then $e \ast x = x$ for all x, so for all x. Solving for e, I get . Therefore, I {\it guess} that 3 is the identity.

Next, I'll confirm my guess by checking the axiom. Let $x \in \real$ . Then

$3 \ast x = 3 + x - 3 = x \quad\hbox{and}\quad x \ast 3 = x + 3 - 3 = x.$

Therefore, 3 is the identity.

Next, I'll work backwards to guess a formula for the inverse of an element. Let $x \in \real$ . Then the inverse $x^{-1}$ must satisfy $x \ast x^{-1} = 3$ , since 3 is the identity. Therefore, $x + x^{-1} - 3 = 3$ , so $x^{-1} = 6 - x$ . Therefore, I guess that is the inverse of x.

Next, I'll confirm my guess by checking the axiom. Let $x \in \real$ . Then

$x\ast (6 - x) = x + (6 - x) - 3 = 3 \quad\hbox{and}\quad (6 - x) \ast x = (6 - x) + x - 3 = 3.$

Therefore, is the inverse of x, and every element has an inverse.

Many mathematical structures which arise in algebra involve one or two binary operations which satisfy certain axioms.

Definition.

A monoid is a set with an associative binary operation.

A semigroup is a set with an associative binary operation which has an identity element.

A group is a set with an associative binary operation which has an identity element and in which every element has an inverse.

Example. $\integer$ , $\rational$ , $\real$ , and $\complex$ are groups under the usual addition operations.

$\integer$ , $\rational$ , $\real$ , and $\complex$ are semigroups under the usual multiplication operations. They aren't groups, because all of them contain 0, which does not have a multiplicative inverse.

Example. I saw above that the binary operation $\ast$ on $\real$ given by

$x \ast y = x + y - 3$

makes $\real$ into a group. Note that this operation is different from the addition operation: A given set can be made into a group in many ways.

Example. ( A binary operation on loops) Take a subset X of $\real^n$ and pick a point P as the basepoint. Consider the set of loops which start and end at P.

To be precise, a loop is a continuous function $f: [0, 1] \to X$ such that and . Think of the parametrized curves you saw in calculus, for example.

Define an operation on loops by taking loops a and b and letting $a\ast b$ be the loop formed by going around a, then going around b.

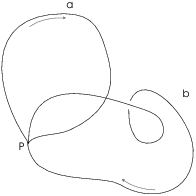
$\hbox{\epsfysize=1.75in \epsffile{binop1.eps}}$

Since both a and b start and end at P, the result is a loop starting and ending at P.

The precise definition of $a\ast b$ is as follows. If $a, b: [0, 1] \to X$ , then

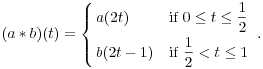
$(a\ast b)(t) = \cases{ a(2t) & if $0 \le t \le \dfrac{1}{2}$ \cr \noalign{\vskip2pt} b(2t - 1) & if $\dfrac{1}{2} < t \le 1$ \cr}.$

This traces out a as t goes from 0 to $\dfrac{1}{2}$ , then traces out b as t goes from $\dfrac{1}{2}$ to 1.

This gives a binary operation on the set of loops. Unfortunately, it isn't quite associative as is. If you have 3 loops a, b, and c, then $(a\ast b)\ast c$ will trace out a for $0 \le t \le \dfrac{1}{4}$ , b for $\dfrac{1}{4} \le t \le \dfrac{1}{2}$ , and c for $\dfrac{1}{2} \le t \le 1$ . On the other hand, $a\ast (b\ast c)$ will trace out a for $0 \le t \le \dfrac{1}{2}$ , b for $\dfrac{1}{2} \le t \le \dfrac{3}{4}$ , and c for $\dfrac{3}{4} \le t \le 1$ .

I could fix this problem by considering equivalence classes of loops instead of loops. Define two loops to be equivalent if they have the same image --- that is, if they "trace out the same curve". The operation above is still defined on equivalence classes of loops, and becomes an associative operation. In fact, it has an identity element, namely the loop which consists of the point P alone.

Thus, the set of equivalence classes of loops with this operation is a semigroup.

In order to make the set into a group, I need a different equivalence relation called loop homotopy. Roughly speaking, two loops will be homotopic if one can be continuously deformed into the other with X, such that the starting and ending point P doesn't move during the deformation. The resulting group is called the fundamental group of X; it is studied in a branch of mathematics called algebraic topology.

Contact information

Bruce Ikenaga's Home Page