Direct Proof

A direct proof uses the facts of mathematics, the rules of inference, and any special assumptions ( premises or hypotheses) to draw a conclusion.

In contrast, an indirect proof (or proof by contradiction) starts by assuming in addition the negation of the desired conclusion. When you reach a contradiction, you know that the negation of the conclusion must be false, so the conclusion must be true.

We'll consider direct proofs in this section and some that follow; proof by contradiction will be discussed later.

Example. Prove that the product of two consecutive integers plus the larger of the two integers is a perfect square.

For example, 5 and 6 are consecutive integers. Their product, plus the larger of the two, is $5\cdot 6 + 6 = 36$ , which is $6^2$ .

An example is not a proof. All my example has shown is that the statement is true for 5 and 6. It gives me no particular reason for believing that the statement will be true for 293841 and 293842.

How can I represent two consecutive integers in symbolic form? Suppose n is the smaller of the two integers. Then the next integer after n is $n + 1$ . Now I have names for my integers: n and $n + 1$ .

Next, I'll translate the given statement into symbols.

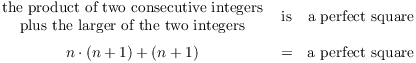
$$\matrix{\matrix{\hbox{the product of two consecutive integers} \cr \hbox{plus the larger of the two integers} \cr} & \hbox{is} & \hbox{a perfect square} \cr & & \cr n\cdot (n + 1) + (n + 1) & = & \hbox{a perfect square} \cr}$$

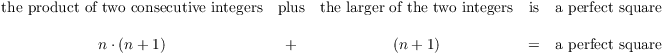
$$\matrix{\hbox{the product of two consecutive integers} & \hbox{plus} & \hbox{the larger of the two integers} & \hbox{is} & \hbox{a perfect square} \cr & & & & \cr n\cdot (n + 1) & + & (n + 1) & = & \hbox{a perfect square} \cr}$$

I could make a symbol for the right side --- "$m^2$ ", for instance. (If I do this, I must not use "$n^2$ ", because n already has a meaning.) But since I have an equation to prove, I'll just start on the left side and do algebra and see if I can get to the right side.

$$n\cdot (n + 1) + (n + 1) = n^2 + n + n + 1 = n^2 + 2 n + 1 = (n + 1)^2.$$

$(n + 1)^2$ is a perfect square, since it is the square of the integer $n + 1$ . That's what I want.

If I clean up my proof, here is how it would look.

A pair of consecutive integers has the form n, $n + 1$ , where n is an integer. The product of the two consecutive integers plus the larger of the two integers is $n(n + 1) + (n + 1)$ . I want to show that this is a perfect square.

By elementary algebra,

$$n \cdot (n + 1) + (n + 1) = n^2 + n + n + 1 = n^2 + 2 n + 1 = (n + 1)^2.$$

$(n + 1)^2$ is a perfect square, since it is the square of the integer $n + 1$ .

This proves that the product of two consecutive integers plus the larger of the two integers is a perfect square.

Notice that I was careful to state what the symbol n stood for when I introduced it. In the next sentence, I explained how I was getting the expression $n(n + 1) + (n + 1)$ . I also stated what I was planning to prove.

The computation involves elementary algebra, so it isn't necessary to explain each individual step. But I did say that it was just elementary algebra, so a reader would know that there's nothing fancy or complicated going on.

When I got $(n + 1)^2$ , I explained why it was what I wanted.

Finally, I indicated that the proof was finished by stating what I had proved, and tacking on the end-of-proof symbol (\halmos).

You can often discover proofs by working backwards from what you want to prove, but you should be careful not to work backwards in presenting a proof.

Example. Prove that if x is a nonzero real nuber, then

$$x^6 + \dfrac{16}{x^6} \ge 8.$$

On scratch paper, I might work backwards to figure out what to do:

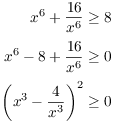
$$\eqalign{ x^6 + \dfrac{16}{x^6} & \ge 8 \cr \noalign{\vskip2pt} x^6 - 8 + \dfrac{16}{x^6} & \ge 0 \cr \noalign{\vskip2pt} \left(x^3 - \dfrac{4}{x^3}\right)^2 & \ge 0 \cr}$$

The last line is true, because squares are always nonnegative. But what I just wrote is scratch work, not a proof. You can't start a proof by assuming what you want to prove.

I'll discuss this in more detail below, but here's one way to think about it: If you're trying to show that "$x^6 + \dfrac{16}{x^6} \ge 8$ " is true and I start with it, then it's true --- so why do I need to write anything else?

Maybe you would say: "It's only conditionally true until it's confirmed by getting something true". But math doesn't work that way --- something is either true or false, and we don't prove things by "confirmation". (This is a big difference from everyday life.)

Here is how I would write the proof correctly. I start with something I know is true, then work till I get the thing I'm trying to prove. So:

Since squares are nonnegative,

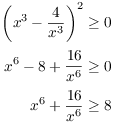
$$\eqalign{ \left(x^3 - \dfrac{4}{x^3}\right)^2 & \ge 0 \cr \noalign{\vskip2pt} x^6 - 8 + \dfrac{16}{x^6} & \ge 0 \cr \noalign{\vskip2pt} x^6 + \dfrac{16}{x^6} & \ge 8 \cr}$$

There are others ways to write this proof. For instance, you could have started with $(x^6 - 4)^2 \ge 0$ . If you do this, you will need to use the fact that $x \ne 0$ and the fact that $x^6 \ge 0$ to justify all the steps. (See if you can tell why.)

An important point made by the last example is:

$$\hbox{When you're writing a proof, don't start with what you want to prove.}$$

Assuming what you want to prove is known as begging the question. It is a very easy mistake to make, because in everyday life you often reason by confirmation. That is, you make a guess, then collect evidence and see if your guess is confirmed. However, logic doesn't support this kind of reasoning.

Suppose that you know that $P \ifthen Q$ is true, and you also know that Q is true. Do you know that P is true?

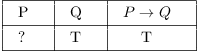
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & P & & Q & & $P \ifthen Q$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & ? & & T & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

If you examine the truth table for $P \ifthen Q$ , you can see that in this case P could be either true or false. In other words, if an implication ($P \ifthen Q$ ) is true and the conclusion (Q) is true, you can't conclude that the premise (P) is true.

For instance, this is a valid sequence of algebra steps:

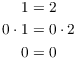
$$\eqalign{ 1 & = 2 \cr 0 \cdot 1 & = 0 \cdot 2 \cr 0 & = 0 \cr}$$

Also, the conclusion "$0 = 0$ " is true. But obviously, "$1 = 2$ " is false.

Thus, if you start with the thing you want to prove and wind up with something that is true --- like "$0 = 0$ " --- that doesn't prove that the thing you started with is true.

If your "proof" ends with a statement like "$0 = 0$ ", "$x = x$ ", "$a + b = a + b$ ", and so on, you may be assuming what you want to prove. At the very least, the arrangement of your proof is incorrect.

If you want to work backwards from what you want to prove to discover a proof, do so on scratch paper. Be sure that when you write the proof that you start with mathematical facts or given assumptions.

Example. Prove that if $x \in \real$ , then

$$4 \sin x + 2 e^x + x^2 + 2 x + 5 > 0.$$

I'll let you try to work backwards to discover the proof that I'll present.

We will use a combination of mathematical facts.

From trigonometry,

$$\sin x \ge -1, \quad\hbox{so}\quad 4 \sin x \ge -4.$$

Since the exponential function is always positive,

$$e^x > 0, \quad\hbox{so}\quad 2 e^x > 0.$$

Since squares are nonnegative,

$$(x + 1)^2 \ge 0, \quad\hbox{so}\quad x^2 + 2 x + 1 \ge 0.$$

If I add $4 \sin x \ge -4$ and $2 e^x > 0$ and $x^2 + 2 x + 1 \ge 0$ , I get

$$\eqalign{ 4 \sin x + 2 e^x + x^2 + 2 x + 1 & > -4 \cr 4 \sin x + 2 e^x + x^2 + 2 x + 5 & > 0 \cr} \quad\halmos$$

Example. Prove that if x and y are nonnegative real numbers, then

$$\dfrac{x + y}{2} \ge \sqrt{x y}.$$

(This is called the Arithmetic-Geometric Mean Inequality.)

I'll try to figure out the proof by working backwards from what I want to prove. (So all of this is scratchwork!)

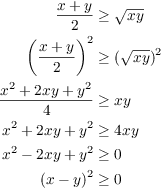
$$\eqalign{ \dfrac{x + y}{2} & \ge \sqrt{x y} \cr \left(\dfrac{x + y}{2}\right)^2 & \ge (\sqrt{x y})^2 \cr \dfrac{x^2 + 2 x y + y^2}{4} & \ge x y \cr x^2 + 2 x y + y^2 & \ge 4xy \cr x^2 - 2 x y + y^2 & \ge 0 \cr (x - y)^2 & \ge 0 \cr}$$

At this point, I notice that I've obtained a true statement: A square must be greater than or equal to 0. To write the "real" proof, I'll just reverse the steps I did, checking at each point that the algebra is still valid.

( The real proof.) Suppose x and y are nonnegative real numbers. Since a square must be greater than or equal to 0, I have

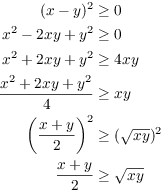
$$\eqalign{ (x - y)^2 & \ge 0 \cr x^2 - 2 x y + y^2 & \ge 0 \cr x^2 + 2 x y + y^2 & \ge 4 x y \cr \dfrac{x^2 + 2 x y + y^2}{4} & \ge x y \cr \left(\dfrac{x + y}{2}\right)^2 & \ge (\sqrt{x y})^2 \cr \dfrac{x + y}{2} & \ge \sqrt{x y} \cr}$$

In taking the square root of both sides in the last step, I didn't need to use absolute values, because x and y (and hence $\dfrac{x + y}{2}$ and $\sqrt{x y}$ ) are nonnegative.

When you write a proof, you usually omit any scratchwork that you used to discover it. It is like removing the scaffolding after you've constructed a building. However, it can make proofs look mysterious --- if you only saw the real proof above, you might have wondered how anyone would have thought to start with $(x - y)^2 \ge 0$ . So it's worthwhile when you're teaching to let people in on the secret and show how the proof was discovered --- as long as you don't substitute scratchwork for the real thing.

Example. (The Triangle Inequality) Let $x, y \in \real$ . Prove that

$$|x + y| \le |x| + |y|.$$

("$\real$ " is the symbol for the real numbers, and $\in$ means "is an element of". So "$x, y \in \real$ " means that x and y are real numbers.)

I'll give the proof in finished form before I discuss it.

Since $|x| \ge x$ and $|y| \ge y$ ,

$$|x| + |y| \ge x + y.$$

In addition, $x \ge -|x|$ and $y \ge -|y|$ , so

$$x + y \ge -|x| - |y| = -(|x| + |y|).$$

Multiplying by -1 flips the inequality, so

$$|x| + |y| \ge -(x + y).$$

Now $|x| + |y|$ is bigger than a number ($x + y$ ) and the negative of the number ($-(x + y)$ ), so it must be bigger than the absolute value of the number:

$$|x| + |y| \ge |x + y|.$$

When I started to write down this proof, I had what I thought was a neat idea. I don't remember what it was, but I wanted to use the inequality $|x||y| \ge xy$ . After a while, I decided that $|x||y| \ge xy$ was wrong, and wrote down the proof above instead. I even remarked on my "mistake" in an earlier version of these notes, as an example of a false start at a proof.

Later, a student asked why $|x||y| \ge x y$ was wrong. I stared at it for a while, then realized it was right! I still don't remember the neat idea I had for using it to do the proof, however.

In most math books and papers, you'll see proofs written down like the one above. Rarely do you read a discussion of the author's false starts and confusions. But math is a human activity, and people are imperfect. In writing proofs, you may often make mistakes --- hopefully, better mistakes than the one I made! --- and you will often get stuck. Don't let the polished proofs that you see in books lead you to believe that writing proofs is supposed to be easy --- or that, if it isn't, then there's something wrong with you. Writing proofs is one of the most difficult mental activities anyone can attempt.

Now that you know the Triangle Inequality, you can use it to prove other results.

Example. Use the Triangle Inequality to prove:

(a) If $x \in \real$ , then $|x^2 + x| + |x - 1| \ge |x^2 + 1|$ .

(b) If $a, b, c, d \in \real$ , then $|a - b| + |c - b| + |c - d| \ge |a - d|$ .

(a) Note that $|x - 1| = |1 - x|$ . So

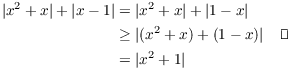
$$\eqalign{ |x^2 + x| + |x - 1| & = |x^2 + x| + |1 - x| \cr & \ge |(x^2 + x) + (1 - x)| \cr & = |x^2 + 1| \cr} \quad\halmos$$

(b) Note that $|c - b| = |b - c|$ . So

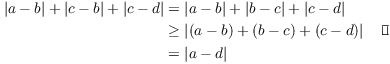
$$\eqalign{ |a - b| + |c - b| + |c - d| & = |a - b| + |b - c| + |c - d| \cr & \ge |(a - b) + (b - c) + (c - d)| \cr & = |a - d| \cr} \quad\halmos$$

Sometimes proofs use facts that you've seen in basic algebra. For example, squares are nonnegative: If $u \in real$ , then

$$u^2 \ge 0.$$

You may need to use facts from trigonometry. If $u \in \real$ , then you have inequalities

$$-1 \le \sin u \le 1 \quad\hbox{and}\quad -1 \le \cos u \le 1.$$

Or you may need trig identities, such as

$$(\sin u)^2 + (\cos u)^2 = 1.$$

Example. Prove that if $x \in \real$ , then

$$x^2 - 8 x + 5 \cos 3 x + 21 \ge 0.$$

Since squares are nonnegative,

$$(x - 4)^2 \ge 0.$$

Since $\cos (\hbox{anything}) \ge -1$ ,

$$\cos 3 x \ge -1, \quad\hbox{so}\quad 5 \cos 3 x \ge -5.$$

Adding the inequalities, I get

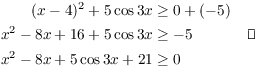
$$\eqalign{ (x - 4)^2 + 5 \cos 3 x & \ge 0 + (-5) \cr x^2 - 8 x + 16 + 5 \cos 3 x & \ge -5 \cr x^2 - 8 x + 5 \cos 3 x + 21 & \ge 0 \cr} \quad\halmos$$

Example. Discuss the following "proof by picture": You are trying to show that the angles in a triangle add up to $180^\circ$ .

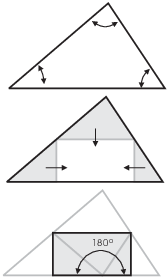
$$\hbox{\epsfysize=2.5in \epsffile{direct-proof1.eps}}$$

Take the triangle and fold the top down as shown in the second picture so that the top vertex just touches the base with the fold parallel to the base. Then fold the other two corners in from the left and right.

The original angles of the triangle have been folded together into a straight angle ($180^\circ$ ). Therefore, the angles in a triangle add up to $180^\circ$ .

A picture can be helpful in understanding something. It can even be so convincing that it seems like a "proof by picture".

This looks very convincing, and it's actually a good thing to show students in geoemtry class. But as a proof, it has difficulties.

For one thing, I did the construction for a specific triangle. How do I know it will work with any triangle? What if the triangle is obtuse, for example? What if it's a right triangle with one side perpendicular to the base?

$$\hbox{\epsfysize=1in \epsffile{direct-proof2.eps}}$$

Moreover, I asserted that the corners would fit together as shown, but I didn't prove that it would work.

In general, you should be very careful in your use of pictures. You can (and should) use them to clarify your explanations. But a picture is not a substitute for a rigorous argument.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga