Divisibility

Definition. If a and b are integers, then a divides b if $a n = b$ for some integer n. In this case, a is a factor or a divisor of b.

The notation $a \mid b$ means "a divides b".

The notation $a \notdiv b$ means a does not divide b.

Notice that divisibility is defined in terms of multiplication --- there is no mention of a "division" operation. The definition agrees with ordinary usage: For example, 12 divides 48, because $12 \cdot 4 = 48$ . It does have the following peculiar consequence: $0 \mid 0$ because (for instance) $0 \cdot 417 = 0$ . You may object that "you can't divide by 0", but that is a different use of the word "divide" --- it refers to multiplying by the multiplicative inverse, and it's true that 0 doesn't have a multiplicative inverse in any "reasonable" number system.

If this still troubles you, there's no great harm in adding the condition "$a \ne 0$ " to the definition above.

Here are some things to keep in mind when writing proofs involving divisibility:

(a) It's often useful to translate divisibility statements (like $a \mid b$ ) into equations using the definition.

(b) Do not use fractions or the division operation ("$/$ " or "$\div$ ") in your proofs!

Proposition. Let a, b, and c be integers.

(a) If $a \mid b$ and $b \mid c$ , then $a \mid c$ .

(b) If $a \mid x$ and $a \mid y$ , then $a \mid (b x + c y)$ for all $b, c \in \integer$ .

Proof. (a) Suppose $a \mid b$ and $b \mid c$ . Now $a \mid b$ means that $a m = b$ for some m and $b \mid c$ means that $b n = c$ for some n. Hence, $a m n = c$ , so $a \mid c$ .

(b) Suppose $a \mid x$ and $a \mid y$ . Now $a \mid x$ means that $a m = x$ for some m and $a \mid y$ means that $a n = y$ for some n. Then

$$b x + c y = b a m + c a n = a(b m + c n), \quad\hbox{so}\quad a \mid b x + c y.\quad\halmos$$

An expression of the form $b x + c y$ is called a linear combination of x and y.

Here are some special cases of part (b):

1. If a divides x and y, then a divides $x + y$ and $x - y$ .

2. If a divides x, then a divides $b x$ for all b.

In the first case, apply (b) with $b = 1$ and $c = 1$ (and $b = 1$ and $c = -1$ ). In the second case, apply (b) $c = 0$ .

Example. Suppose n is an integer. Prove that the only positive integer that divides both $2 n + 3$ and $3 n + 4$ is 1.

Suppose k is a positive integer and $k \mid 2 n + 3$ and $k \mid 3 n + 4$ . Then by part (b) of the preceding proposition, k divides any linear combination of $2 n + 3$ and $3 n + 4$ . I'll choose a combination so that the n-terms cancel:

$$k \mid 3 \cdot (2 n + 3) - 2 \cdot (3 n + 4) = 1.$$

So k is a positive integer which divides 1 --- but the only positive integer which divides 1 is 1. Hence, $k = 1$ .

Definition. An integer $n > 1$ is prime if the only positive divisors of n are 1 and n. An integer $n > 1$ which is not prime is composite.

For example, the first few primes are

$$2, 3, 5, 7, 11, 13, \ldots.$$

On the other hand, the first few composite numbers are

$$4, 6, 8, 9, 10, \ldots.$$

Proposition. If n is composite, then there are integers a and b such that $1 < a, b < n$ and $n = ab$ .

Proof. Since n is composite, it is not prime. Therefore, n has a positive divisor a other than 1 and n. Suppose $n = a b$ . I still have to show that $1 < a, b < n$ .

Note that if $b = 1$ , then $a = n$ (contradiction), and if $b = n$ , then $a = 1$ (contradiction). So a and b are both different from 1 and n.

Suppose on the contrary that $a > n$ . Since $b > 1$ , it follows that

$$n = a b > n \cdot 1 = n.$$

This is a contradiction.

Likewise, if $b > n$ , then since $a > 1$ , I have

$$n = a b > 1 \cdot n = n.$$

This is a contradiction.

Now I know that a and b are positive integers which are not greater than n, and neither is 1 or n. This implies that $1 < a, b < n$ .

Proposition. Every integer $n > 1$ has a prime factor.

Proof. I'll use induction, starting with $n = 2$ . In fact, 2 has a prime factor, namely 2.

Suppose that $n > 2$ , and that every integer k less than n has a prime factor. I must show that n has a prime factor.

If n is prime, then n has a prime factor, namely itself. So assume n is composite.

By the last lemma, there are integers a and b such that $1 < a, b < n$ and $n = a b$ . If either a or b is prime, then I have a prime factor of n. Suppose then that a and b are both composite. In this case, since $a < n$ , I know that a must have a prime factor, by induction. But a prime factor of a is a prime factor of n, by transitivity of divisibility. This completes the induction step, and the proof.

I sketched the proof of the following result when I discuss proof by contradiction. Having proved the last two results, the proof is now complete --- but I'll repeat it here. It is essentially the proof in Book IX of Euclid's Elements.

Theorem. There are infinitely many primes.

Proof. Suppose on the contrary that there are only finitely many primes

$$p_1, p_2, \ldots, p_n.$$

Consider the number

$$p_1 p_2 \cdots p_n + 1.$$

When this number is divided by $p_1$ , $p_2$ , ..., $p_n$ , it leaves a remainder of 1. Therefore, it has no prime factors. This contradicts the preceding lemma. Hence, there must be infinitely many primes.

The situation changes greatly if you consider primes of a restricted form. For example, it's not known whether there are infinitely many Mersenne primes --- primes of the form $2^n - 1$ , where $n > 1$ .

Proposition. If n is composite, then it has a prime factor p such that $p \le \sqrt{n}$ .

Proof. First, an earlier result shows that there are integers a and b such that $1 < a, b < n$ and $n = a b$ . If $a > \sqrt{n}$ and $b > \sqrt{n}$ , then $n = a b > (\sqrt{n})(\sqrt{n}) = n$ , which is a contradiction. Therefore, a and b can't both be greater than $\sqrt{n}$ .

Suppose without loss of generality that $a \le \sqrt{n}$ . Then either a is prime or a has a prime factor, by the preceding lemma. In either case, I have a prime less than or equal to $\sqrt{n}$ which divides a, and hence divides n.

Example. Use trial division to determine whether 163 is prime.

By the last lemma, to test whether n is prime, divide n in succession by the primes less than $\sqrt{n}$ . If no such prime divides n, then n is prime.

I have $\sqrt{163} = 12.76715 \ldots$ . By trial, I find that

$$2 \notdiv 163, \quad 3 \notdiv 163, \quad 5 \notdiv 163, \quad 7 \notdiv 163, \quad 11 \notdiv 163.$$

Since these are all the primes less than $\sqrt{163}$ , it follows that 163 is prime.

There are simple tests for divisibility by small numbers based on the decimal representation of a number.

If $a_n\, a_{n-1} \ldots a_1\, a_0$ is the decimal representation of a number, its digital sum is

$$D(a_n\, a_{n-1} \ldots a_1\, a_0) = a_n + a_{n-1} + \cdots + a_1 + a_0.$$

That is, $D(x)$ is the sum of the digits of x. For example,

$$D(119) = 1 + 1 + 9 = 11, \quad D(247) = 2 + 4 + 7 = 13.$$

Proposition. (a) A number is even (divisible by 2) if and only if its units digit is 0, 2, 4, 6, or 8.

(b) A number is divisible by 5 if and only if its unit digit is 0 or 5.

(c) A number is divisible by 3 if and only if its digital sum is divisible by 3.

(d) A number is divisible by 9 if and only if its digital sum is divisible by 9.

Proof. Suppose $x = a_n\, a_{n - 1} \ldots a_1\, a_0$ is the decimal representation of a positive integer x. Then

$$x = a_n \cdot 10^n + a_{n - 1} \cdot 10^{n - 1} + \cdots + a_1 \cdot 10 + a_0.$$

All of the results can be proved by using this representation (and where appropriate, the digital sum). For example, here's a sketch of the proof of (a). Note that since $2 \mid 10$ ,

$$2 \mid a_n \cdot 10^n, 2 \mid a_{n - 1} \cdot 10^{n - 1}, \ldots, 2 \mid a_1 \cdot 10.$$

Thus, for some integer m,

$$x = 2 m + a_0.$$

From this, it follows that $2 \mid x$ if and only if $a_0$ is 0, 2, 4, 6, or 8. I'll let you write out the details.

For (c) and (d), note that

$$x - D(x) = (a_n \cdot 10^n + a_{n - 1} \cdot 10^{n - 1 } + \cdots + a_1 \cdot 10 + + a_0) - (a_n + a_{n - 1} + \cdots + a_1 + a_0) =$$

$$a_n (10^n - 1) + a_{n - 1} (10^{n - 1} - 1) + \cdots + a_1 (10 - 1).$$

Each term of the form $10^k - 1$ is $999 \ldots 9$ ($k - 1$ nines), so the right side is divisible by 3 and by 9. Thus, $x - D(x)$ is divisible by 3 and 9, so x is divisible by 3 or 9 if and only if $D(x)$ is.

If you're uncomfortable about using the decimal representation of $10^k - 1$ as $999 \ldots 9$ , you can note that for $k \ge 1$ ,

$$10^k - 1 = (10 - 1)(10^{k - 1} + 10^{k - 2} + \cdots + 10 + 1) = 9 (10^{k - 1} + 10^{k - 2} + \cdots + 10 + 1).$$

Hence, $9 \mid 10^k - 1$ .

For example, 9183 is divisible by 3, since $9 + 1 + 8 + 3 = 21$ is divisible by 3. And 725 is not divisible by 9, because $7 + 2 + 5 = 14$ is not divisible by 9.

Remark. The Fundamental Theorem of Arithmetic states that every positive integer greater than 1 can be expressed as a product of powers of primes, and this expression is unique up to the order of the factors.

For example,

$$720 = 2^4 \cdot 3^2 \cdot 5.$$

Here is a sketch of the proof that every positive integer greater than 1 can be expressed as a product of powers of primes. Do a generalized induction: $n = 2$ is a product of a single prime (namely 2), and that is the basis step. Take an integer $n > 2$ , and suppose every integer greater than 1 and less than n can be written as a product of powers of primes. If n is prime, we're done (since a prime is product of a single prime, namely itself). If n is not prime, an earlier result show it can be factored as $n = a b$ , where $1 < a, b < n$ . By the induction hypothesis, factor a and b into products of powers of primes. Then putting their factorizations together shows n factors into a product of powers of primes.

The proof that a factorization into a product of powers of primes is unique up to the order of factors uses additional results on divisibility (e.g. Euclid's lemma), so I will omit it.

While this result is very important, overuse of the Fundamental Theorem in divisibility proofs often results in sloppy proofs which obscure important ideas. Try to write your proofs in other ways.

Definition. Let m and n be integers, not both 0. The greatest common divisor $(m, n)$ of m and n is the largest integer which divides both m and n.

The reason for not defining "$(0, 0)$ " is that any integer divides both 0 and 0 (e.g. $4571 \mid 0$ because $4571 \cdot 0 = 0$ ), so there is no largest integer which divides both 0 and 0.

Here are some numerical examples:

$$(6, 8) = 2, \quad (-15, 10) = 5, \quad (77, 0) = 77.$$

Proposition. Let m and n be integers, not both 0.

(a) $(m, n) \ge 1$ .

(b) $(m, n) = (|m|, |n|)$ .

(c) $(m, n) \mid m$ and $(m, n) \mid n$ .

(d) If a and b are integers, then

$$(m, n) \mid a m + b n.$$

Proof. (a) 1 is a common divisor of any two integers m and n. Since $(m, n)$ is the greatest common divisor, $(m, n) \ge 1$ .

(In particular, $(m, n)$ must be positive.)

(b) First, I'll show m and $|m|$ have the same divisors. If $k \mid m$ , then $m = a k$ for some integer a. So $-m = (-a) k$ , and hence $k \mid -m$ . But $|m|$ is either m or $-m$ , and hence $k \mid |m|$ .

Conversely, suppose $k \mid |m|$ --- say $|m| = a k$ for some integer a. If $|m| = m$ , then $k \mid m$ . And if $|m| = -m$ , then $a k = -m$ , so $(-a) k = m$ , and $k \mid m$ .

Thus, m and $|m|$ have the same divisors, and likewise n and $|n|$ have the same divisors. It follows that the common divisors of m and n are the same as the common divisors of $|m|$ and $|n|$ . Since the sets of common divisors are the same, their largest elements must be the same --- that is, $(m, n) = (|m|, |n|)$ .

(This means that when you compute the greatest common divisor of two numbers, you can take absolute values to get two positive numbers.)

(c) This follows from the definition: $(m, n)$ (is the largest integer which) divides both m and n.

(d) Since $(m, n) \mid m$ and $(m, n) \mid n$ , we have $(m, n) \mid a m + b n$ by an earlier divisibility result.

You might be able find the greatest common divisor of two relatively small numbers by factoring. But what if the numbers are too big to be factored? The Euclidean algorithm gives a method for computing the greatest common divisor of two positive integers using only integer division.

Example. Compute $(271, 113)$ .

I'll arrange the computations in a table with two columns. Begin the first column with the larger number first. Divide 271 by 113:

$$271 = 2 \cdot 113 + 45.$$

Put the quotient 2 next to the 113 and the reaminder 45 below the 113.

(Note that there is a blank space (marked with a "-") next to 271. This isn't important here, but later you may see a third column added to this table for the Extended Euclidean Algorithm, in which case the blank space is important.)

Continue in the same fashion: Divide 113 by 45:

$$113 = 2 \cdot 45 + 23.$$

Put the quotient 2 next to 45 and the remainder 23 below 45.

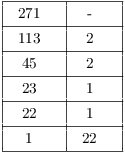
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 271 & & - & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 113 & & 2 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 45 & & 2 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 23 & & 1 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 22 & & 1 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 1 & & 22 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

The table stops when you get an a first column number "divides evenly into" the one above it. The the remainder is 0, and since you can't divide by 0, the process must stop. The last nonzero remainder is the greatest common divisor. So

$$(271, 113) = 1.$$

You can at least see from this example why the process has to stop. When you divide, the remainder is always less that the thing you divided by. So the remainders in the first column are positive numbers that keep getting smaller --- and since the process can't go on forever (reason: the Well-Ordering Axiom for the positive integers), it must end in the only way possible with a remainder of 0.

I won't prove that this algorithm gives the greatest common divisor, but here's the idea: The greatest common divisor of any two consecutive numbers in the first column remains the same. Check it yourself in the table above.

Example. Show that if n is an integer, then $(n, n + 2)$ is either 1 or 2.

$(n, n + 2)$ divides both n and $n + 2$ , so it divides any linear combination of n and $n + 2$ . In particular,

$$(n, n + 2) \mid (n + 2) - n = 2.$$

Now $(n, n + 2) \ge 1$ ; the only positive integers which divide 2 are 1 and 2. Therefore, $(n, n + 2)$ is either 1 or 2.

Notice that both of these cases can occur: If $n = 1$ , then $(n, n + 2) = (1,3) = 1$ , and if $n = 2$ , $(n, n + 2) = (2, 4) = 2$ .

Proposition. If $a m + b n = 1$ for some $a, b \in \integer$ , then $(m, n) = 1$ .

Proof. $(m, n) \mid m$ and $(m, n) \mid n$ , so

$$(m, n) \mid a m + b n = 1.$$

But $(m, n) \ge 1$ , and the only positive integer which divides 1 is 1. Therefore, $(m, n) = 1$ .

Definition. Let $m, n \in \integer$ . m and n are relatively prime if $(m, n) = 1$ .

Thus, the last lemma says that if some linear combination of m and n equals 1, then m and n are relatively prime.

Example. Prove that for all $n \in \integer$ , $4 n + 3$ and $6 n + 4$ are relatively prime.

Two integers are relatively prime if their only (positive) common factor is 1. Thus, this problem says that 1 is the only common factor of $4n + 3$ and $6n + 4$ .

The table below shows the values of $4n + 3$ and $6 n + 4$ for $-5 \le n \le 5$ . The result seems plausible based on the evidence.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & n & & -5 & & -4 & & -3 & & -2 & & -1 & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $4n + 3$ & & -17 & & -13 & & -9 & & -5 & & -1 & & 3 & & 7 & & 11 & & 15 & & 19 & & 23 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $6n + 4$ & & -26 & & -20 & & -14 & & -8 & & -2 & & 4 & & 10 & & 16 & & 22 & & 28 & & 34 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

To prove it, I'll use part (a). I want numbers a and b such that

$$a (4 n + 3) + b (6 n + 4) = 1.$$

Since there are no n's on the right side, I want to choose a and b to make the n's on the left cancel out. One way to do this is

$$3 \cdot (4 n + 3) + (-2) (6 n + 4) = 1.$$

This linear combination is equal to 1, so by (a), $(4 n + 3, 6 n + 4) = 1$ .

As the example shows, one way of showing that two integers are relatively prime is to find a linear combination of them that equals 1. The converse is true: If two integers are relatively prime, then some linear combination of the integers equals 1.

In fact, more is true: The greatest common divisor $(m, n)$ of m and n can always be written as a linear combination $a m + b n$ of m and n. An extended version of the Euclidean algorithm finds a linear combination $a m + b n$ such that $(m, n) = a m + b n$ . You'll probably see this result in a course in abstract algebra or number theory; I won't prove it here.

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga