Existence Proofs

An existence proof shows that an object exists. In some cases, this means displaying the object, or giving a method for finding it.

Example. Show that there is a real number x such that $\sin x > 0$ but $\cos x < 0$ .

There are many possibilities; for example,

$$\sin \dfrac{3\pi}{4} = \dfrac{\sqrt{2}}{2}, \quad\hbox{but}\quad \cos \dfrac{3\pi}{4} = -\dfrac{\sqrt{2}}{2}.\quad\halmos$$

Example. Show that there is a real number x such that $x^2 + 30 < 11 x$ .

Rewrite the inequality as

$$x^2 - 11 x + 30 < 0, \quad\hbox{or}\quad (x - 5)(x - 6) < 0.$$

The graph of $y = (x - 5)(x - 6)$ looks like this:

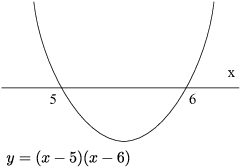
$$\hbox{\epsfysize=1.5in \epsffile{existence-proofs1.eps}}$$

The graph lies below the x-axis between $x = 5$ and $x = 6$ . So, for example, $x = 5.5$ meets the conditions:

$$5.5^2 - 11 \cdot 5.5 + 30 = -0.25 < 0.\quad\halmos$$

In some cases, you can know that an object exists without having any way of finding it (or finding it exactly). By analogy:

(a) If you throw your keys into a corn field, you know your keys are in the field --- but you may have trouble finding them!

(b) You know that Calvin Butterball has a birthday, even though you don't know what day it is.

You've seen results of this kind in calculus. One such result is:

Theorem. ( The Intermediate Value Theorem:) Let f be a continuous function on the interval $[a, b]$ . Suppose that c is a number between $f(a)$ and $f(b)$ . Then $f(x) = c$ for some x in the interval $[a, b]$ .

The Intermediate Value Theorem does not tell you how to find an x such that $f(x) = c$ --- it simply guarantees that such an x exists.

Example. Show that there is a real number x such that $x = \cos x$ .

The assertion means that the graphs of $y = x$ and $y = \cos x$ intersect:

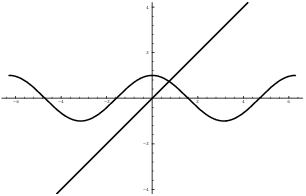
$$\hbox{\epsfysize=1.75in \epsffile{existence-proofs2.eps}}$$

It looks like they do. Note, however, that a picture is not a proof.

Let $f(x) = \cos x - x$ . Then

$$f(0) = \cos 0 - 0 = 1, \quad\hbox{while}\quad f(\pi) = \cos \pi - \pi = -1 - \pi.$$

Since $f(0)$ is positive and $f(\pi)$ is negative, and since f is continuous for all x, the Intermediate Value Theorem implies that there is an x between 0 and $\pi$ for which $f(x) = 0$ . Then $\cos x - x = 0$ , so $\cos x = x$ .

Notice that the Intermediate Value Theorem doesn't tell you what x is, or how to find it. (It's approximately 0.73909.)

Example. Suppose f is a continuous function satisfying

$$f(5) = 11 \quad\hbox{and}\quad f(8) = -20.$$

Prove that there is a number c such that $5 \le c \le 8$ and

$$3 c + f(c) = 10.$$

The function $g(x) = 3 x + f(x)$ is continuous.

$$g(5) = 3 \cdot 5 + f(5) = 15 + 11 = 26 \quad\hbox{and}\quad g(8) = 3 \cdot 8 + (-20) = 4.$$

Since 10 is between 26 and 4, there is a number c such that $5 \le c \le 8$ and

$$g(c) = 3 c + f(c) = 10.\quad\halmos$$

To say that there is an x satisfying a certain property does not mean that there is only one x satisfying the property. If that is what is meant, it has to be stated explicitly. Hence, there might be many values which satisfy the conclusion of the Intermediate Value Theorem.

Here's another existence theorem from calculus:

Theorem. ( Mean Value Theorem) Suppose f is function which is continuous on the closed interval $a \le x \le b$ and differentiable on the open interval $a < x < b$ . Then there is a number c such that $a < c < b$ and

$$f'(c) = \dfrac{f(b) - f(a)}{b - a}.$$

Example. Find a number c which satisfies the conclusion of the Mean Value Theorem when it is applied to $f(x) = x^3$ on the interval $1 \le x \le 3$ .

Note that

$$\dfrac{f(3) - f(1)}{3 - 1} = 13.$$

Now $f'(x) = 3 x^2$ , so setting $3 c^2 = 13$ , I find that $c = \pm\sqrt{\dfrac{13}{3}}$ . Both of these values satisfy the conclusion of the Mean Value Theorem.

Example. Suppose f is a differentiable function satisfying

$$f(-2) = 10 \quad\hbox{and}\quad f'(x) > 3 \quad\hbox{for all}\quad x.$$

Prove that $f(5) > 31$ .

Applying the Mean Value Theorem to f on the interval $-2 \le x \le 5$ gives a number c such that $-2 < c < 5$ and

$$\dfrac{f(5) - f(-2)}{5 - (-2)} = f'(c).$$

Then

$$\eqalign{ \dfrac{f(5) - f(-2)}{5 - (-2)} & = f'(c) > 3 \cr \noalign{\vskip2pt} \dfrac{f(5) - 10}{7} & > 3 \cr \noalign{\vskip2pt} f(5) - 10 & > 21 \cr f(5) & > 31 \cr}\quad\halmos$$

Rolle's theorem is special case of the Mean Value Theorem: With the assumptions of the theorem, if $f(a) = f(b)$ , then there is a number c such that $a < c < b$ and

$$f'(c) = 0.$$

That is, c is a critical point of f.

Example. Let $f(x) = x^2 \sin x$ . Prove that there is a number c between 1 and $\pi$ such that $f'(c) = 0$ .

f is differentiable. Moreover,

$$f(0) = 0 \quad\hbox{and}\quad f(\pi) = 0.$$

By Rolle's theorem, there is a number c between 0 and $\pi$ such that $f'(c) = 0$ .

In the last example, I found numbers satisfying the conclusion of the theorem --- but again, there is no guarantee that I can find such numbers explicitly. The theorem just says that at least one such number exists.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga