Limits

The definition of a limit involves both universal and existential quantifiers.

Let f be a function from the real numbers to the real numbers, and let c be a real number. Assume that f is defined on a open interval containing c. The statement $\displaystyle \lim_{x \to c} f(x) = L$ means:

For every $\epsilon > 0$ , there is a $\delta > 0$ , such that if $\delta > |x - c| > 0$ , then $\epsilon > |f(x) - L|$ .

Think of $\delta$ as a thermostat, as the actual temperature in a room, and L as the ideal temperature. Someone challenges you to make the actual temperature fall within a certain tolerance $\epsilon$ of the ideal temperature L. You must do that by setting your $\delta$ -thermostat appropriately (so that x is sufficiently close to c).

Moreover, note that it says "for every $\epsilon > 0$ ". It's isn't enough for you to say what you'd do if you were challenged with $\epsilon = 0.1$ or $\epsilon = 0.000004$ . You must prove that you can meet the challenge no matter what $\epsilon$ you're challenged with.

Finally, note the stipulation " ". This implies that $x \ne c$ , since gives . Thus, the conclusion " $\epsilon > |f(x) - L|$ " must hold only for x's close to c, but not necessarily for . (It may hold for , but it doesn't have to.)

What does this mean? It's a precise way of saying that the value of the limit of as x approaches c does not depend on what does at --- over even whether is defined.

For example, consider the functions whose graphs are shown below.

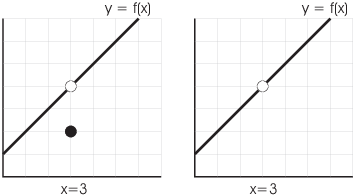
$\hbox{\epsfysize=1.75in \epsffile{limits1.eps}}$

In both cases,

$\lim_{x \to 3} f(x) = 4.$

In the first case, : The value of the function at is different from the value of the limit.

In the second case, is undefined.

The fact that $\displaystyle \lim_{x \to 3} f(x) \ne f(3)$ means that f is not continuous at .

Example. Use the $\epsilon-\delta$ definition of the limit to prove that

$\lim_{x \to 2} (5 x + 4) = 14.$

In this case, , , and . So here is what I need to prove.

Suppose $\epsilon > 0$ . I must find a $\delta > 0$ such that if $\delta > |x - 2| > 0$ , then $\epsilon > |(5 x + 4) - 14|$ .

Note that at this point $\epsilon$ is fixed --- given --- but all you can assume is that it's some positive number. Since it is given, however, I can use it in finding an appropriate $\delta$ .

I'll show how to find $\delta$ by working backwards; then I'll write the proof "forwards", the way you should write it.

I want

$\epsilon > |(5 x + 4) - 14|, \quad\hbox{or}\quad \epsilon > |5 x - 10|, \quad\hbox{or}\quad \dfrac{\epsilon}{5} > |x - 2|.$

It looks like I should set $\delta = \dfrac{\epsilon}{5}$ .

All of this has been on "scratch paper"; now here's the real proof.

Suppose $\epsilon > 0$ . Let $\delta = \dfrac{\epsilon}{5}$ . If $\delta > |x - 2| > 0$ , then

$\dfrac{\epsilon}{5} > |x - 2|, \quad\hbox{so}\quad \epsilon > |5 x - 10|, \quad\hbox{or}\quad \epsilon > |(5 x + 4) - 14|.$

Thus, if $\delta = \dfrac{\epsilon}{5}$ and $\delta > |x - 2| > 0$ , then $\epsilon > |(5 x + 4) - 14|$ . This proves that $\displaystyle \lim_{x \to 2} (5 x + 4) = 14$ .

Example. Let

$f(x) = \cases{3 x + 4 & if $x < 1$ \cr 9 - 2 x & if $x \ge 1$ \cr}.$

Use the $\epsilon-\delta$ definition of the limit to prove that

$\lim_{x \to 1} f(x) = 7.$

Let $\epsilon > 0$ . I must find $\delta > 0$ such that if $\delta > |x - 1| > 0$ , then $\epsilon > |f(x) - 7|$ .

Here's my scratch work. First, for ,

$\epsilon > |f(x) - 7|, \quad \epsilon > |(3 x + 4) - 7|, \quad \epsilon > |3 x - 3|, \quad \dfrac{\epsilon}{3} > |x - 1|.$

It looks like I should take $\delta = \dfrac{\epsilon}{3}$ .

For ,

$\epsilon > |f(x) - 7|, \quad \epsilon > |(9 - 2 x) - 7|, \quad \epsilon > |2 - 2 x| = |2 x - 2|, \quad \dfrac{\epsilon}{2} > |x - 1|.$

It looks like I should take $\delta = \dfrac{\epsilon}{2}$ .

In order to ensure that both the and requirements are satisfied, I'll take $\delta$ to be the smaller of the two: $\delta = \dfrac{\epsilon}{3}$ .

Now here's the proof written out correctly.

Suppose $\epsilon > 0$ . Let $\delta = \dfrac{\epsilon}{3}$ , and assume that $\delta > |x - 1| > 0$ .

If , then

$\dfrac{\epsilon}{3} > |x - 1|, \quad\hbox{so}\quad \epsilon > |3 x - 3| = |(3 x + 4) - 7| = |f(x) - 7|.$

Now consider the case . Since $\dfrac{\epsilon}{3} > |x - 1|$ , and since $\dfrac{\epsilon}{2} > \dfrac{\epsilon}{3}$ , I have $\dfrac{\epsilon}{2} > |x - 1|$ . Therefore,

$\epsilon > |2 x - 2| = |2 - 2 x| = |(9 - 2 x) - 7| = |f(x) - 7|.$

(The case is ruled out because .)

Thus, taking $\delta = \dfrac{\epsilon}{3}$ guarantees that if $\delta > |x - 1| > 0$ , then $\epsilon > |f(x) - 7|$ . This proves that $\displaystyle \lim_{x \to 1} f(x) = 7$ .

Example. Use the $\epsilon-\delta$ definition of the limit to prove that

$\lim_{x \to 2} x^2 = 4.$

Let $\epsilon > 0$ . I want to find $\delta > 0$ such that if $\delta > |x - 2| > 0$ , then $\epsilon > |x^2 - 4|$ .

I start out as usual with my scratch work:

$\epsilon > |x^2 - 4| = |x - 2||x + 2|.$

Now I have a problem. I can use $\delta$ to control , but what do I do about ?

The idea is this: Since I have complete control over $\delta$ , I can assume $\delta \le 1$ . When I finally set $\delta$ , I can make it smaller if necessary to ensure that this condition is met.

Now if $\delta \le 1$ , then , so , and . In particular, the biggest could be is 5. So now

$\epsilon > |x - 2||x + 2| \quad\hbox{becomes}\quad \epsilon > |x - 2|\cdot 5, \quad\hbox{so}\quad \dfrac{\epsilon}{5} > |x - 2|.$

This inequality suggests that I set $\delta = \dfrac{\epsilon}{5}$ --- but then I remember that I needed to assume $\delta \le 1$ . I can meet both of these conditions by setting $\delta$ to the smaller of 1 and $\dfrac{\epsilon}{5}$ : that is, $\delta = \min\left(1,\dfrac{\epsilon}{5}\right)$ .

That was scratchwork; now here's the real proof.

Let $\epsilon > 0$ . Set $\delta = \min\left(1,\dfrac{\epsilon}{5}\right)$ . Suppose $\delta > |x - 2| > 0$ .

Since $\delta \le 1$ , I have

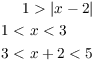
$\eqalign{ 1 & > |x - 2| \cr 1 <\ & x < 3 \cr 3 <\ & x + 2 < 5 \cr}$

Therefore, .

Now $\delta \le \dfrac{\epsilon}{5}$ , so $\dfrac{\epsilon}{5} > |x - 2|$ .

Now multiply the inequalities and $\dfrac{\epsilon}{5} > |x - 2|$ :

$\epsilon = \dfrac{\epsilon}{5}\cdot 5 > |x - 2||x + 2| = |x^2 - 4|.$

Thus, if $\delta = \min\left(1,\dfrac{\epsilon}{5}\right)$ and $\delta > |x - 2| > 0$ , then $\epsilon > |x^2 - 4|$ . This proves that $\displaystyle\lim_{x \to 2} x^2 = 4$ .

Example. Prove that $\displaystyle \lim_{x \to 2} \dfrac{x^2 + 11}{x + 3} = 3$ .

Let $\epsilon > 0$ . I must find $\delta$ such that if $\delta > |x - 2| > 0$ , then $\epsilon > \left|\dfrac{x^2 + 11}{x + 3} - 3\right|$ .

I'll start with some scratchwork.

$\left|\dfrac{x^2 + 11}{x + 3} - 3\right| = \left|\dfrac{x^2 + 11 - 3(x + 3)}{x + 3}\right| = \left|\dfrac{x^2 - 3 x + 2}{x + 3}\right| = \left|\dfrac{(x - 2)(x - 1)}{x + 3}\right| = |x - 2|\left|\dfrac{x - 1}{x + 3}\right|.$

I can use $\delta$ to control directly. I need to control the size of $\left|\dfrac{x - 1}{x + 3}\right|$ . It's important to think of this as $|x - 1|\cdot \left|\dfrac{1}{x + 3}\right|$ , not as and !

Assume $1 \ge \delta$ . Then , so .

For , , so .

For $\left|\dfrac{1}{x + 3}\right|$ , , so $\dfrac{1}{4} > \dfrac{1}{x + 3} > \dfrac{1}{6}$ , and $\left|\dfrac{1}{x + 3}\right| < \dfrac{1}{4}$ .

Since all the number involved are positive, I can multiply the inequalities to obtain

$2\cdot \dfrac{1}{4} > |x - 1|\cdot \left|\dfrac{1}{x + 3}\right|, \quad\hbox{or}\quad \dfrac{1}{2} > |x - 1|\cdot \left|\dfrac{1}{x + 3}\right|.$

Thus, I'll get $\epsilon > |x - 2|\left|\dfrac{x - 1}{x + 3}\right|$ if I have $\epsilon > |x - 2|\cdot \dfrac{1}{2}$ , or $2\epsilon > |x - 2|$ . Here's the proof.