Proof by Cases

You can sometimes prove a statement by:

1. Dividing the situation into cases which exhaust all the possibilities; and

2. Showing that the statement follows in all cases.

It's important to cover all the possibilities. And don't confuse this with trying examples; an example is not a proof.

Note that there are usually many ways to divide a situation into cases. For example, if I know that x is a real number and I'm proving something about x, here are some ways I could take cases:

(a) $x > 0$ , $x = 0$ , or $x < 0$ .

(b) $|x| > 1$ or $|x| \le 1$ .

(c) $x \ge \pi$ or $x < \pi$

(d) x is rational or x is irrational.

There are an infinite number of ways to divide up the real numbers to take cases; how you do it depends on what you're trying to prove. In general, you should try to use a small number of cases --- and in particular, you should see if you can give a proof without taking cases at all!

I'll begin with a logic proof. In this situation, your cases are usually P and $\lnot P$ , where P is a statement.

Example. Premises: 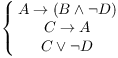$\left\{\matrix{A \ifthen (B \land \lnot D) \cr C \ifthen A \cr C \lor \lnot D \cr}\right.$

Prove: $\lnot D$ .

I can divide the situation into two cases: Either C is true, or $\lnot C$ is true. These exhaust the possibilities, by the Law of the Excluded Middle. I'll assume each in turn and show that I can derive $\lnot D$ .

$$\matrix{ \hfill 1. & A \ifthen (B \land \lnot D) \hfill & \hbox{Premise} \hfill \cr \hfill 2. & C \ifthen A \hfill & \hbox{Premise} \hfill \cr \hfill 3. & C \lor \lnot D \hfill & \hbox{Premise} \hfill \cr \hfill 4. & C \hfill & \hbox{Premise - Case 1} \hfill \cr \hfill 5. & A \hfill & \hbox{Modus ponens (2,4)} \hfill \cr \hfill 6. & B \land \lnot D \hfill & \hbox{Modus ponens (1,5)} \hfill \cr \hfill 7. & \lnot D \hfill & \hbox{Decomposing a conjunction (6)} \hfill \cr \hfill 8. & \lnot C \hfill & \hbox{Premise - Case 2} \hfill \cr \hfill 9. & \lnot D \hfill & \hbox{Disjunctive syllogism (3,8)} \hfill \cr \hfill 10. & \lnot D \hfill & \hbox{Proof by cases (4,7,8,9)} \hfill \cr }$$

Since both of my cases led to the conclusion $\lnot D$ , and since my cases exhausted the possibilities, I've proved $\lnot D$ .

In logic proofs, cases of the form P and $\lnot P$ where P is some statement will cover all possibilities, since one of P or $\lnot P$ must be true. So these are the natural cases to take in logic proofs.

How did I know to use C and $\lnot C$ rather than (say) B and $\lnot B$ ? I looked at my premises and noticed that I could do something with each of those assumptions: C could be used for modus ponens, and $\lnot C$ could be used for disjunctive syllogism. As with many logic proofs, it was a matter of looking ahead or working backward.

Note: You may use the premises for the proof in either case, but you may not use a statement derived for one case in the other case.

For example, in the first case, I derived the statement A at line 5. I may not use A anywhere in the second case.

Example. In calculus, you learned Rolle's theorem. Here's the statement:

Let f be a function which is continuous on the interval $a \le x \le b$ and is differentiable on the interval $a < x < b$ . Suppose $f(a) = f(b) = 0$ . Then there is a real number c such that $a < c < b$ and $f'(c) = 0$ .

In other words (to put it roughly), between two roots there must be a horizontal tangent.

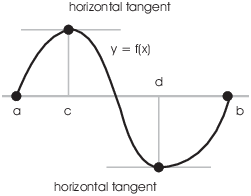
$$\hbox{\epsfysize=1.75in \epsffile{proof-by-cases-1.eps}}$$

Prove Rolle's Theorem by taking cases.

There are three cases: f is never positive or negative on the interval $a \le x \le b$ , f is positive somewhere on the interval $a \le x \le b$ , or f is negative somewhere on the interval $a \le x \le b$ .

Suppose first that f is never positive or negative on the interval $a \le x \le b$ . Then $f = 0$ , a constant function, and $f'(x) = 0$ for all x in the interval $a < x < b$ .

Suppose that f is positive at some point of the interval $a \le x \le b$ . A continuous function on a closed interval attains a maximum value on the interval; since I already know f is positive somewhere, the maximum value of f must be positive. Since f is 0 at the endpoints, it must attain the maximum value at some point c in the open interval $a < x < b$ .

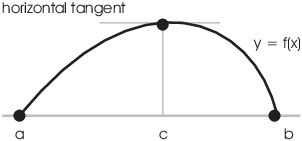
$$\hbox{\epsfysize=1.25in \epsffile{proof-by-cases-2.eps}}$$

Since $a < c < b$ , f is differentiable at c. But at a point where a differentiable function attains a maximum, the derivative is 0. Therefore, $f'(c) = 0$ .

Suppose that f is negative at some point of the interval $a \le x \le b$ . A continuous function on a closed interval attains a minimum value on the interval; since I already know f is negative somewhere, the minimum value of f must be negative. Since f is 0 at the endpoints, it must attain the minimum value at some point c in the open interval $a < x < b$ .

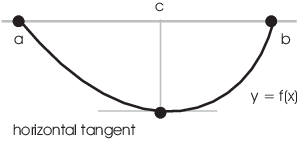
$$\hbox{\epsfysize=1.25in \epsffile{proof-by-cases-3.eps}}$$

Since $a < c < b$ , f is differentiable at c. But at a point where a differentiable function attains a minimum, the derivative is 0. Therefore, $f'(c) = 0$ .

Since the three cases exhaust all the possibilities, this proves that $f'(c) = 0$ for some c in the interval $a < x < b$ .

Many problems involving divisibility of integers use the Division Algorithm. It is a consequence of the Well-Ordering Axiom for the positive integers, which is also the basis for mathematical induction.

Theorem. (Division Algorithm) Let m and n be integers, where $n > 0$ . Then there are unique integers q and r such that

$$m = n q + r, \quad\hbox{where}\quad 0 \le r < n.$$

("q" stands for "quotient" and "r" stands for "remainder".)

I won't give a proof of this, but here are some examples which show how it's used.

Example. Apply the Division Algorithm to:

(a) Divide 31 by 8.

(b) Divide -31 by 8.

(c) Divide an integer m by 2.

(a) Let $m = 31$ and $n = 8$ . Then I have

$$31 = 8 \cdot 3 + 7.$$

In this case, $q = 3$ and $r = 7$ . Note that $0 \le 7 < 8$ holds --- when you divide, the remainder should be nonnegative, and less than the number you divided by.

(b) (a) Let $m = -31$ and $n = 8$ . Then I have

$$-31 = 8 \cdot (-4) + 1.$$

In this case, $q = -4$ and $r = 1$ . Again, $0 \le 1 < 8$ holds. Note that if I wrote "$-31 = 8 \cdot (-3) + (-7)$ ", the equation is true, but the numbers aren't the ones produced by the Division Algorithm --- r is not allowed to be negative.

(c) Take m to be an integer, and let $n = 2$ . Then

$$m = 2 q + r, \quad\hbox{where}\quad 0 \le r < 2.$$

Now since r is an integer and $0 \le r < 2$ , I must have $r = 0$ or $r = 1$ . Thus, if $m \in \integer$ , then

$$m = 2 q \quad\hbox{or}\quad m = 2 q + 1.$$

Of course, the first case occurs when m is even, and the second case occurs when m is odd. If a problem involves odd or even integers, you might consider taking cases in this way.

A similar situation occurs when n is any positive integer. For example, if $m \in \integer$ and $n = 5$ , then

$$m = 5 q + r, \quad\hbox{where}\quad 0 \le r < 5.$$

The condition $0 \le r < 5$ means $r = 0$ , $r = 1$ , $r = 2$ , $r = 3$ , or $r = 4$ . So if $m \in \integer$ , the possibilities are

$$m = 5 q, \quad m = 5 q + 1, \quad m = 5 q + 2, \quad m = 5 q + 3, \quad\hbox{or}\quad m = 5 q + 4.$$

If a problem involves divisibility by 5 you might consider taking cases in this way.

(When I discuss modular arithmetic, there will be an easier way to deal with these cases.)

Example. Prove that if n is an integer, then $3 n^2 + n + 14$ is even.

Let $n \in \integer$ . I'll consider two cases: n is even and n is odd.

Case 1. n is even.

Since n is even, I can write $n = 2 k$ , where $k \in \integer$ . Then

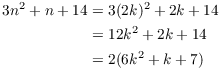
$$\eqalign{ 3 n^2 + n + 14 & = 3(2 k)^2 + 2 k + 14 \cr & = 12 k^2 + 2 k + 14 \cr & = 2(6 k^2 + k + 7) \cr}$$

Since $6 k^2 + k + 7$ is an integer, $3 n^2 + n + 14$ is even if n is even.

Case 2. n is odd.

Since n is odd, I can write $n = 2 k + 1$ , where $k \in \integer$ . Then

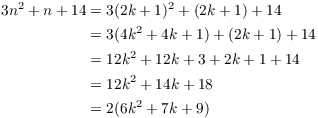
$$\eqalign{3 n^2 + n + 14 & = 3(2 k + 1)^2 + (2 k + 1) + 14 \cr & = 3(4 k^2 + 4 k + 1) + (2 k + 1) + 14 \cr & = 12 k^2 + 12 k + 3 + 2 k + 1 + 14 \cr & = 12 k^2 + 14 k + 18 \cr & = 2(6 k^2 + 7 k + 9) \cr}$$

Since $6 k^2 + 7 k + 9$ is an integer, $3 n^2 + n + 14$ is even if n is odd.

Since in both cases $3 n^2 + n + 14$ is even, it follows that if n is an integer, then $3 n^2 + n + 14$ is even.

Example. Prove that if n is an integer, then $2 n^2 + n + 1$ is not divisible by 3.

When n is divided by 3, the possible remainders are 0, 1, or 2. I consider these three cases.

Case 1. When n is divided by 3, the remainder is 0.

Then $n = 3 q + 0 = 3 q$ for some integer q. So

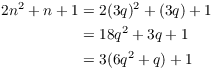
$$\eqalign{ 2 n^2 + n + 1 & = 2 (3 q)^2 + (3 q) + 1 \cr & = 18 q^2 + 3 q + 1 \cr & = 3 (6 q^2 + q) + 1 \cr}$$

The last expression shows that in this case when $2 n^2 + n + 1$ is divided by 3, the remainder is 1. Hence, $2 n^2 + n + 1$ is not divisible by 3.

Case 2. When n is divided by 3, the remainder is 1.

Then $n = 3 q + 1$ for some integer q. So

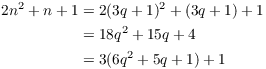
$$\eqalign{ 2 n^2 + n + 1 & = 2 (3 q + 1)^2 + (3 q + 1) + 1 \cr & = 18 q^2 + 15 q + 4 \cr & = 3 (6 q^2 + 5 q + 1) + 1 \cr}$$

The last expression shows that in this case when $2 n^2 + n + 1$ is divided by 3, the remainder is 1. Hence, $2 n^2 + n + 1$ is not divisible by 3.

Case 3. When n is divided by 3, the remainder is 2.

Then $n = 3 q + 2$ for some integer q. So

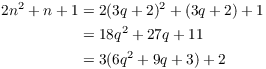
$$\eqalign{ 2 n^2 + n + 1 & = 2 (3 q + 2)^2 + (3 q + 2) + 1 \cr & = 18 q^2 + 27 q + 11 \cr & = 3 (6 q^2 + 9 q + 3) + 2 \cr}$$

The last expression shows that in this case when $2 n^2 + n + 1$ is divided by 3, the remainder is 2. Hence, $2 n^2 + n + 1$ is not divisible by 3.

Since in every case $2 n^2 + n + 1$ is not divisible by 3, it follows that $2 n^2 + n + 1$ is not divisible by 3 for any integer n.

Example. Prove that for all $x \in \real$ ,

$$-5 \le |x + 2| - |x - 3| \le 5.$$

You often think of taking cases in dealing with absolute values. I have

$$|x + 2| = \cases{ x + 2 & if $x + 2 > 0$ \cr -(x + 2) & if $x + 2 \le 0$ \cr}.$$

Now $x + 2 > 0$ means $x > -2$ , and $x + 2 \le 0$ means $x \le -2$ . So

$$|x + 2| = \cases{ x + 2 & if $x > -2$ \cr -(x + 2) & if $x \le -2$ \cr}.$$

In the same way,

$$|x - 3| = \cases{ x - 3 & if $x > 3$ \cr -(x - 3) & if $x \le 3$ \cr}.$$

Given the way the functions are broken apart, I'll consider the cases $x \le -2$ , $-2 < x \le 3$ , and $x > 3$ . Notice that all real numbers are in one of the three cases.

Case 1. $x \le -2$ . In this case,

$$|x + 2| - |x - 3| = -(x + 2) - [-(x - 3)] = -5.$$

Therefore, $-5 \le |x + 2| - |x - 3| \le 5$ holds in this case.

Case 2. $-2 < x \le 3$ . In this case,

$$|x + 2| - |x - 3| = (x + 2) - [-(x - 3)] = 2 x - 1.$$

I have to do some additional work to see whether the target inequality holds. I have

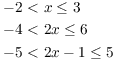
$$\eqalign{ -2 < & \ x \le 3 \cr -4 < & \ 2 x \le 6 \cr -5 < & \ 2 x - 1 \le 5 \cr}$$

Therefore, $-5 \le |x + 2| - |x - 3| \le 5$ holds in this case.

Case 3. $x > 3$ . In this case,

$$|x + 2| - |x - 3| = (x + 2) - (x - 3) = 5.$$

Therefore, $-5 \le |x + 2| - |x - 3| \le 5$ holds in this case.

Since $-5 \le |x + 2| - |x - 3| \le 5$ holds all three cases, it is true for all $x \in \real$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga