Rules of Inference and Logic Proofs

A proof is an argument from hypotheses (assumptions) to a conclusion. Each step of the argument follows the laws of logic. In mathematics, a statement is not accepted as valid or correct unless it is accompanied by a proof. This insistence on proof is one of the things that sets mathematics apart from other subjects.

Writing proofs is difficult; there are no procedures which you can follow which will guarantee success. The patterns which proofs follow are complicated, and there are a lot of them. You can't expect to do proofs by following rules, memorizing formulas, or looking at a few examples in a book.

For this reason, I'll start by discussing logic proofs. Since they are more highly patterned than most proofs, they are a good place to start. They'll be written in column format, with each step justified by a rule of inference. Most of the rules of inference will come from tautologies. Since a tautology is a statement which is "always true", it makes sense to use them in drawing conclusions.

Like most proofs, logic proofs usually begin with premises --- statements that you're allowed to assume. The conclusion is the statement that you need to prove. The idea is to operate on the premises using rules of inference until you arrive at the conclusion.

Rule of Premises. You may write down a premise at any point in a proof.

The second rule of inference is one that you'll use in most logic proofs. It is sometimes called modus ponendo ponens, but I'll use a shorter name.

Modus Ponens. If you know P and $P \ifthen Q$ , you may write down Q.

In the rules of inference, it's understood that symbols like "P" and "Q" may be replaced by any statements, including compound statements. I'll say more about this later.

Here is a simple proof using modus ponens:

$\matrix{ 1. \hfill & P \hfill & \hbox{Premise} \hfill \cr 2. \hfill & P \ifthen Q \hfill & \hbox{Premise} \hfill \cr 3. \hfill & Q \hfill & \hbox{Modus ponens (1, 2)} \hfill \cr}$

I'll write logic proofs in 3 columns. The statements in logic proofs are numbered so that you can refer to them, and the numbers go in the first column. The actual statements go in the second column. The third column contains your justification for writing down the statement.

Thus, statements 1 (P) and 2 ( $P \ifthen Q$ ) are premises, so the rule of premises allows me to write them down. Modus ponens says that if I've already written down P and $P \ifthen Q$ --- on any earlier lines, in either order --- then I may write down Q. I did that in line 3, citing the rule ("Modus ponens") and the lines (1 and 2) which contained the statements I needed to apply modus ponens.

As I noted, the "P" and "Q" in the modus ponens rule can actually stand for compound statements --- they don't have to be "single letters". For example:

$\matrix{ 1. \hfill & (A \lor \lnot B) \ifthen \lnot C \hfill & \hbox{Premise} \hfill \cr 2. \hfill & \lnot D \hfill & \hbox{Premise} \hfill \cr 3. \hfill & A \lor \lnot B \hfill & \hbox{Premise} \hfill \cr 4. \hfill & \lnot C \hfill & \hbox{Modus ponens (1, 3)} \hfill \cr}$

There are several things to notice here. First, $A \lor \lnot B$ is taking the place of P in the modus ponens rule, and $\lnot C$ is taking the place of Q. That is, $A \lor \lnot B$ and $\lnot C$ are compound statements which are substituted for "P" and "Q" in modus ponens.

Notice also that the if-then statement $(A \lor \lnot B) \ifthen \lnot C$ is listed first and the "if"-part $\lnot C$ is listed second. It doesn't matter which one has been written down first, and long as both pieces have already been written down, you may apply modus ponens.

Finally, the statement $\lnot D$ didn't take part in the modus ponens step. Perhaps this is part of a bigger proof, and $\lnot D$ will be used later. The fact that it came between the two modus ponens pieces doesn't make a difference.

As usual in math, you have to be sure to apply rules exactly. For example, this is not a valid use of modus ponens:

$\matrix{ 1. \hfill & P \hfill & \hbox{Premise} \hfill \cr 2. \hfill & (P \land Q) \ifthen R \hfill & \hbox{Premise} \hfill \cr 3. \hfill & R \hfill & \hbox{INVALID modus ponens!} \hfill \cr}$

Do you see why? To use modus ponens on the if-then statement $(P \land Q) \ifthen R$ , you need the "if"-part, which is $P \land Q$ . You only have P, which is just part of the "if"-part. That's not good enough.

Double Negation. In any statement, you may substitute P for $\lnot \lnot P$ or $\lnot \lnot P$ for P (and write down the new statement).

For example, in this case I'm applying double negation with P replaced by $A \ifthen \lnot C$ :

$\matrix{ 1. \hfill & \lnot[\lnot(A \ifthen \lnot C)] \hfill & \hbox{Premise} \hfill \cr 2. \hfill & A \ifthen \lnot C \hfill & \hbox{Double negation (1)} \hfill \cr}$

You can also apply double negation "inside" another statement:

$\matrix{ 1. \hfill & A \ifthen \lnot \lnot B \hfill & \hbox{Premise} \hfill \cr 2. \hfill & A \ifthen B \hfill & \hbox{Double negation (1)} \hfill \cr}$

Double negation comes up often enough that, we'll bend the rules and allow it to be used without doing so as a separate step or mentioning it explicitly. I'll demonstrate this in the examples for some of the other rules of inference.

Modus Tollens. If you know $\lnot Q$ and $P \ifthen Q$ , you may write down $\lnot P$ .

This is a simple example of modus tollens:

$\matrix{ 1. \hfill & \lnot Q \hfill & \hbox{Premise} \hfill \cr 2. \hfill & P \ifthen Q \hfill & \hbox{Premise} \hfill \cr 3. \hfill & \lnot P \hfill & \hbox{Modus tollens (1, 2)} \hfill \cr}$

In the next example, I'm applying modus tollens with P replaced by C and Q replaced by $A \ifthen B$ :

$\matrix{ 1. \hfill & \lnot (A \ifthen B) \hfill & \hbox{Premise} \hfill \cr 2. \hfill & C \ifthen (A \ifthen B) \hfill & \hbox{Premise} \hfill \cr 3. \hfill & \lnot C \hfill & \hbox{Modus tollens (1, 2)} \hfill \cr}$

The last example shows how you're allowed to "suppress" double negation steps. Do you see how this was done? If I wrote the double negation step explicitly, it would look like this:

$\matrix{ 1. \hfill & \lnot (A \ifthen B) \hfill & \hbox{Premise} \hfill \cr 2. \hfill & C \ifthen (A \ifthen B) \hfill & \hbox{Premise} \hfill \cr 3. \hfill & C \ifthen \lnot \lnot(A \ifthen B) \hfill & \hbox{Double negation (2)} \hfill \cr 4. \hfill & \lnot C \hfill & \hbox{Modus tollens (1, 3)} \hfill \cr}$

When you apply modus tollens to an if-then statement, be sure that you have the negation of the "then"-part. The following derivation is incorrect:

$\matrix{ 1. \hfill & Q \hfill & \hbox{Premise} \hfill \cr 2. \hfill & P \ifthen Q \hfill & \hbox{Premise} \hfill \cr 3. \hfill & \lnot P \hfill & \hbox{INVALID modus tollens!} \hfill \cr}$

To use modus tollens, you need $\lnot Q$ , not Q.

This is also incorrect:

$\matrix{ 1. \hfill & Q \hfill & \hbox{Premise} \hfill \cr 2. \hfill & P \ifthen Q \hfill & \hbox{Premise} \hfill \cr 3. \hfill & P \hfill & \hbox{INVALID modus tollens!} \hfill \cr}$

This looks like modus ponens, but backwards. There is no rule that allows you to do this: The deduction is invalid.

Disjunctive Syllogism. If you know $\lnot P$ and $P \lor Q$ , you may write down Q.

Here's a simple example of disjunctive syllogism:

$\matrix{ 1. \hfill & \lnot P \hfill & \hbox{Premise} \hfill \cr 2. \hfill & P \lor Q \hfill & \hbox{Premise} \hfill \cr 3. \hfill & Q \hfill & \hbox{Disjunctive syllogism (1, 2)} \hfill \cr}$

In the next example, I'm applying disjunctive syllogism with $A \lor B$ replacing P and D replacing Q in the rule:

$\matrix{ 1. \hfill & \lnot(A \lor B) \hfill & \hbox{Premise} \hfill \cr 2. \hfill & (A \lor B) \lor D \hfill & \hbox{Premise} \hfill \cr 3. \hfill & D \hfill & \hbox{Disjunctive syllogism (1, 2)} \hfill \cr}$

In the next example, notice that P is the same as $\lnot \lnot P$ , so it's the negation of $\lnot P$ .

$\matrix{ 1. \hfill & P \hfill & \hbox{Premise} \hfill \cr 2. \hfill & \lnot P \lor (Q \ifthen R) \hfill & \hbox{Premise} \hfill \cr 3. \hfill & Q \ifthen R \hfill & \hbox{Disjunctive syllogism (1, 2)} \hfill \cr}$

This is another case where I'm skipping a double negation step. Without skipping the step, the proof would look like this:

$\matrix{ 1. \hfill & P \hfill & \hbox{Premise} \hfill \cr 2. \hfill & \lnot P \lor (Q \ifthen R) \hfill & \hbox{Premise} \hfill \cr 3. \hfill & \lnot \lnot P \hfill & \hbox{Double negation (1)} \hfill \cr 4. \hfill & Q \ifthen R \hfill & \hbox{Disjunctive syllogism (2, 3)} \hfill \cr}$

DeMorgan's Law. In any statement, you may substitute:

1. $\lnot(P \lor Q)$ for $\lnot P \land \lnot Q$ .

2. $\lnot P \land \lnot Q$ for $\lnot(P \lor Q)$ .

3. $\lnot(P \land Q)$ for $\lnot P \lor \lnot Q$ .

4. $\lnot P \lor \lnot Q$ for $\lnot(P \land Q)$ .

As usual, after you've substituted, you write down the new statement.

DeMorgan's Law tells you how to distribute $\lnot$ across $\land$ or $\lor$ , or how to factor $\lnot$ out of $\land$ or $\lor$ . To distribute, you attach $\lnot$ to each term, then change $\land$ to $\lor$ or $\lor$ to $\land$ . To factor, you factor $\lnot$ out of each term, then change $\land$ to $\lor$ or $\lor$ to $\land$ .

Note that it only applies (directly) to "or" and "and". We'll see how to negate an "if-then" later.

Here's DeMorgan applied to an "or" statement:

$\matrix{ 1. \hfill & \lnot(\lnot P \lor \lnot Q) \hfill & \hbox{Premise} \hfill \cr 2. \hfill & P \land Q \hfill & \hbox{DeMorgan (1)} \hfill \cr}$

Notice that a literal application of DeMorgan would have given $\lnot\lnot P \land \lnot\lnot Q$ . I changed this to $P \land Q$ , once again suppressing the double negation step.

Conditional Disjunction. If you know $P \ifthen Q$ , you may write down $\lnot P \lor Q$ .

If you know $\lnot P \lor Q$ , you may write down $P \ifthen Q$ .

Here's the first direction:

$\matrix{ 1. \hfill & \lnot P \lor Q \hfill & \hbox{Premise} \hfill \cr 2. \hfill & P \ifthen Q \hfill & \hbox{Conditional disjunction (1)} \hfill \cr}$

And here's the second:

$\matrix{ 1. \hfill & P \ifthen Q \hfill & \hbox{Premise} \hfill \cr 2. \hfill & \lnot P \lor Q \hfill & \hbox{Conditional disjunction (1)} \hfill \cr}$

The first direction is key: Conditional disjunction allows you to convert "if-then" statements into "or" statements.

We'll see below that biconditional statements can be converted into pairs of conditional statements. Together with conditional disjunction, this allows us in principle to reduce the five logical connectives to three (negation, conjunction, disjunction). But DeMorgan allows us to change conjunctions to disjunctions (or vice versa), so in principle we could do everything with just "or" and "not". The reason we don't is that it would make our statements much longer: The use of the other connectives is like shorthand that saves us writing.

In additional, we can solve the problem of negating a conditional that we mentioned earlier.

$\matrix{ 1. \hfill & \lnot (P \ifthen Q) \hfill & \hbox{Premise} \hfill \cr 2. \hfill & \lnot (\lnot P \lor Q) \hfill & \hbox{Conditional disjunction (1)} \hfill \cr 3. \hfill & P \land \lnot Q \hfill & \hbox{DeMorgan (2)} \hfill \cr}$

We've derived a new rule! Let's write it down.

Negating a Conditional. If you know $\lnot (P \ifthen Q)$ , you may write down $P \land \lnot Q$ .

If you know $P \land \lnot Q$ , you may write down $\lnot (P \ifthen Q)$ .

The first direction is more useful than the second. Personally, I tend to forget this rule and just apply conditional disjunction and DeMorgan when I need to negate a conditional. But you may use this if you wish.

Constructing a Conjunction. If you know P and Q, you may write down $P \land Q$ .

Think about this to ensure that it makes sense to you. If $P \land Q$ is true, you're saying that P is true and that Q is true. So on the other hand, you need both P true and Q true in order to say that $P \land Q$ is true.

Here's an example. Notice that I put the pieces in parentheses to group them after constructing the conjunction.

$\matrix{ 1. \hfill & P \iff Q \hfill & \hbox{Premise} \hfill \cr 2. \hfill & P \lor Q \hfill & \hbox{Premise} \hfill \cr 3. \hfill & (P \iff Q) \land (P \lor Q) \hfill & \hbox{Constructing a conjunction (1, 2)} \hfill \cr}$

Rule of Syllogism. If you know $P \ifthen Q$ and $Q \ifthen R$ , then you may write down $P \ifthen R$ .

The Rule of Syllogism says that you can "chain" syllogisms together. For example:

$\matrix{ 1. \hfill & P \ifthen (Q \lor R) \hfill & \hbox{Premise} \hfill \cr 2. \hfill & (Q \lor R) \ifthen \lnot S \hfill & \hbox{Premise} \hfill \cr 3. \hfill & P \ifthen \lnot S \hfill & \hbox{Rule of syllogism (1, 2)} \hfill \cr}$

Definition of Biconditional. If you know $P \iff Q$ , you may write down $P \ifthen Q$ and you may write down $Q \ifthen P$ . If you know $P \ifthen Q$ and $Q \ifthen P$ , you may write down $P \iff Q$ .

First, a simple example:

$\matrix{ 1. \hfill & P \iff Q \hfill & \hbox{Premise} \hfill \cr 2. \hfill & Q \ifthen P \hfill & \hbox{Definition of biconditional (1)} \hfill \cr}$

By the way, a standard mistake is to apply modus ponens to a biconditional (" $\iff$ "). Modus ponens applies to conditionals (" $\ifthen$ "). So this isn't valid:

$\matrix{ 1. \hfill & P \iff Q \hfill & \hbox{Premise} \hfill \cr 2. \hfill & Q \hfill & \hbox{Premise} \hfill \cr 3. \hfill & P \hfill & \hbox{INVALID - Not modus ponens!} \hfill \cr}$

With the same premises, here's what you need to do:

$\matrix{ 1. \hfill & P \iff Q \hfill & \hbox{Premise} \hfill \cr 2. \hfill & Q \hfill & \hbox{Premise} \hfill \cr 3. \hfill & Q \ifthen P \hfill & \hbox{Definition of biconditional (1)} \hfill \cr 4. \hfill & P \hfill & \hbox{Modus ponens (2, 3) \quad\halmos} \hfill \cr}$

Decomposing a Conjunction. If you know $P \land Q$ , you may write down P and you may write down Q.

This rule says that you can decompose a conjunction to get the individual pieces:

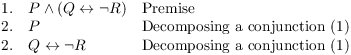
$\matrix{ 1. \hfill & P \land (Q \iff \lnot R) \hfill & \hbox{Premise} \hfill \cr 2. \hfill & P \hfill & \hbox{Decomposing a conjunction (1)} \hfill \cr 2. \hfill & Q \iff \lnot R \hfill & \hbox{Decomposing a conjunction (1)} \hfill \cr}$

Note that you can't decompose a disjunction!

$\matrix{ 1. \hfill & P \lor Q \hfill & \hbox{Premise} \hfill \cr 2. \hfill & P \hfill & \hbox{INVALID!} \hfill \cr}$

What's wrong with this? If you know that $P \lor Q$ is true, you know that one of P or Q must be true. The problem is that you don't know which one is true, so you can't assume that either one in particular is true.

On the other hand, it is easy to construct disjunctions.

Constructing a Disjunction. If you know P, and Q is any statement, you may write down $P \lor Q$ .

This says that if you know a statement, you can "or" it with any other statement to construct a disjunction.

$\matrix{ 1. \hfill & P \hfill & \hbox{Premise} \hfill \cr 2. \hfill & P \lor \hbox{``Calvin sleeps with a night light.''} \hfill & \hbox{Constructing a disjunction (1)} \hfill \cr}$

Notice that it doesn't matter what the other statement is! Once you know that P is true, any "or" statement with P must be true: An "or" statement is true if at least one of the pieces is true.

The next two rules are stated for completeness. They are easy enough that, as with double negation, we'll allow you to use them without a separate step or explicit mention.

Commutativity of Conjunctions. In any statement, you may substitute $P \land Q$ for $Q \land P$ (and write down the new statement).

Commutativity of Disjunctions. In any statement, you may substitute $P \lor Q$ for $Q \lor P$ (and write down the new statement).

Here is commutativity for a conjunction:

$\matrix{ 1. \hfill & P \land \lnot Q \hfill & \hbox{Premise} \hfill \cr 2. \hfill & \lnot Q \land P \hfill & \hbox{Commutativity (1)} \hfill \cr}$

Here is commutativity for a disjunction:

$\matrix{ 1. \hfill & (Q \ifthen P) \lor R \hfill & \hbox{Premise} \hfill \cr 2. \hfill & R \lor (Q \ifthen P) \hfill & \hbox{Commutativity (1)\quad\halmos} \hfill \cr}$

Before I give some examples of logic proofs, I'll explain where the rules of inference come from. You've probably noticed that the rules of inference correspond to tautologies. In fact, you can start with tautologies and use a small number of simple inference rules to derive all the other inference rules.

Three of the simple rules were stated above: The Rule of Premises, Modus Ponens, and Constructing a Conjunction. Here are two others. We've been using them without mention in some of our examples if you look closely.

Equivalence You may replace a statement by another that is logically equivalent. (Recall that P and Q are logically equivalent if and only if $P \iff Q$ is a tautology.)

For instance, since P and $\lnot \lnot P$ are logically equivalent, you can replace P with $\lnot \lnot P$ or $\lnot \lnot P$ with P. This is Double Negation. As I mentioned, we're saving time by not writing out this step.

Substitution. You may take a known tautology and substitute for the simple statements.

This amounts to my remark at the start: In the statement of a rule of inference, the simple statements ("P", "Q", and so on) may stand for compound statements. "May stand for" is the same as saying "may be substituted with". We've been doing this without explicit mention.

Here's an example. The Disjunctive Syllogism tautology says

$(\lnot P \land (P \lor Q)) \ifthen Q.$

Suppose you have $\lnot (A \land D)$ and $(A \land D) \lor C$ as premises. Here's how you'd apply the simple inference rules and the Disjunctive Syllogism tautology:

$\matrix{ 1. \hfill & \lnot (A \land D) \hfill & \hbox{Premise} \hfill \cr 2. \hfill & (A \land D) \lor C \hfill & \hbox{Premise} \hfill \cr 3. \hfill & \lnot (A \land D) \land ((A \land D) \lor C) \hfill & \hbox{Constructing a conjunction (1, 3)} \hfill \cr 4. \hfill & \lnot (A \land D) \land ((A \land D) \lor C) \ifthen C \hfill & \hbox{Substitution (Disjunctive Syllogism)} \hfill \cr 5. \hfill & C \hfill & \hbox{Modus ponens (3, 4)} \hfill \cr}$

Notice that I used four of the five simple inference rules: the Rule of Premises, Modus Ponens, Constructing a Conjunction, and Substitution. In line 4, I used the Disjunctive Syllogism tautology $(\lnot P \land (P \lor Q)) \ifthen Q$ by substituting

$A \land D \quad\hbox{for}\quad P \quad\hbox{and}\quad C \quad\hbox{for}\quad Q.$

(Some people use the word "instantiation" for this kind of substitution.)

The advantage of this approach is that you have only five simple rules of inference. The disadvantage is that the proofs tend to be longer. With the approach I'll use, Disjunctive Syllogism is a rule of inference, and the proof is:

$\matrix{ 1. \hfill & \lnot (A \land D) \hfill & \hbox{Premise} \hfill \cr 2. \hfill & (A \land D) \lor C \hfill & \hbox{Premise} \hfill \cr 3. \hfill & C \hfill & \hbox{Disjunctive syllogism (1,2)} \hfill \cr}$

The approach I'm using turns the tautologies into rules of inference beforehand, and for that reason you won't need to use the Equivalence and Substitution rules that often. But you are allowed to use them, and here's where they might be useful. Suppose you're writing a proof and you'd like to use a rule of inference --- but it wasn't mentioned above. Write down the corresponding logical statement, then construct the truth table to prove it's a tautology (if it isn't on the tautology list). Then use Substitution to use your new tautology.

If you go to the market for pizza, one approach is to buy the ingredients --- the crust, the sauce, the cheese, the toppings --- take everything home, assemble the pizza, and put it in the oven. Using tautologies together with the five simple inference rules is like making the pizza from scratch. But you could also go to the market and buy a frozen pizza, take it home, and put it in the oven. Using lots of rules of inference that come from tautologies --- the approach I'll use --- is like getting the frozen pizza.

Here are some proofs which use the rules of inference. In each case, some premises --- statements that are assumed to be true --- are given, as well as a statement to prove. A proof consists of using the rules of inference to produce the statement to prove from the premises.

Example. Premises: 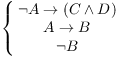$\left\{\matrix{ \lnot A \ifthen (C \land D) \cr A \ifthen B \cr \lnot B \cr}\right.$ .

Prove: C.

$\matrix{ 1. \hfill & A \ifthen B \hfill & \hbox{Premise} \hfill \cr 2. \hfill & \lnot B \hfill & \hbox{Premise} \hfill \cr 3. \hfill & \lnot A \hfill & \hbox{Modus tollens (1,2)} \hfill \cr 4. \hfill & \lnot A \ifthen (C \land D) \hfill & \hbox{Premise} \hfill \cr 5. \hfill & C \land D \hfill & \hbox{Modus ponens (3,4)} \hfill \cr 6. \hfill & C \hfill & \hbox{Decomposing a conjunction (5)} \hfill \cr}$

It is one thing to see that the steps are correct; it's another thing to see how you would think of making them. I used my experience with logical forms combined with working backward.

I'm trying to prove C, so I looked for statements containing C. Only the first premise contains C. I saw that C was contained in the consequent of an if-then; by modus ponens, the consequent follows if you know the antecedent.

The "if"-part of the first premise is $\lnot A$ . Hence, I looked for another premise containing A or $\lnot A$ . The only other premise containing A is the second one. In this case, A appears as the "if"-part of an if-then. By modus tollens, $\lnot A$ follows from the negation of the "then"-part B. But I noticed that I had $\lnot B$ as a premise, so all that remained was to run all those steps forward and write everything up.

It's common in logic proofs (and in math proofs in general) to work backwards from what you want on scratch paper, then write the real proof forward. The second part is important!

In order to do this, I needed to have a hands-on familiarity with the basic rules of inference: Modus ponens, modus tollens, and so forth. You'll acquire this familiarity by writing logic proofs.

You also have to concentrate in order to remember where you are as you work backwards. You may need to scribble stuff on scratch paper to avoid getting confused. Keep practicing, and you'll find that this gets easier with time.

Example. Premises: 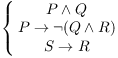$\left\{\matrix{ P \land Q \cr P \ifthen \lnot(Q \land R) \cr S \ifthen R \cr}\right.$ .

Prove: $\lnot S$ .

$\matrix{ 1. \hfill & P \land Q \hfill & \hbox{Premise} \hfill \cr 2. \hfill & P \hfill & \hbox{Decomposing a conjunction (1)} \hfill \cr 3. \hfill & Q \hfill & \hbox{Decomposing a conjunction (1)} \hfill \cr 4. \hfill & P \ifthen \lnot(Q \land R) \hfill & \hbox{Premise} \hfill \cr 5. \hfill & \lnot(Q \land R) \hfill & \hbox{Modus ponens (3,4)} \hfill \cr 6. \hfill & \lnot Q \lor \lnot R \hfill & \hbox{DeMorgan (5)} \hfill \cr 7. \hfill & \lnot R \hfill & \hbox{Disjunctive syllogism (3,6)} \hfill \cr 8. \hfill & S \ifthen R \hfill & \hbox{Premise} \hfill \cr 9. \hfill & \lnot S \hfill & \hbox{Modus tollens (7,8) \quad\halmos} \hfill \cr}$

Example. Premises: 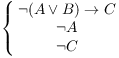$\left\{\matrix{ \lnot (A \lor B) \ifthen C \cr \lnot A \cr \lnot C \cr}\right.$ .

Prove: B.

$\matrix{ 1. \hfill & \lnot (A \lor B) \ifthen C \hfill & \hbox{Premise} \hfill \cr 2. \hfill & \lnot C \hfill & \hbox{Premise} \hfill \cr 3. \hfill & A \lor B \hfill & \hbox{Modus tollens (1,2)} \hfill \cr 4. \hfill & \lnot A \hfill & \hbox{Premise} \hfill \cr 5. \hfill & B \hfill & \hbox{Disjunctive syllogism (3,4)} \hfill \cr}$

Notice that in step 3, I would have gotten $\lnot\lnot(A \lor B)$ . I omitted the double negation step, as I have in other examples.

Contact information

Bruce Ikenaga's Home Page