These problems will illustrate some of the logical concepts we've looked at, as well as illustrating some proof techniques that we'll look at in more detail later. These proofs are written entirely in words, so for the moment we don't need to worry about the presentation details associated with mathematical symbols.
The general setup: You're on an island where each inhabitant is a truth-teller or a liar. Truth-tellers always tell the truth; liars always lie. You're given some information about some people, usually in the form of statements they make. You're asked to determine whether each person is a truth-teller or a liar. In some cases, it may be impossible to determine what everyone is, or the situation may be impossible.
Example. You're on an island where each inhabitant is a truth-teller or a liar. Truth-tellers always tell the truth; liars always lie. Calvin and Phoebe are on the island.
Phoebe says: "If 34 is odd, then I am a truth-teller."
Calvin says: "Phoebe is a liar."
Determine whether each person is a truth-teller or a liar.
(In this problem, I notice that I can determine the truth or falsity of the statement "34 is odd" without knowing anything about Phoebe or Calvin. So I'll start with it and see what follows from it.)
Since "34 is odd" is false, the "if" part of Phoebe's statement is false. Hence, Phoebe's statement is true. Therefore, Phoebe must be a truth-teller.
Now Calvin says "Phoebe is a liar", and that is false, since I just showed that Phoebe is a truth-teller. Therefore, Calvin is a liar.
Thus, Phoebe is a truth-teller and Calvin is a liar.![]()
Here are some general ideas about how you might approach a problem like this. Pick a character in the problem --- let's say you pick "Leopold". Consider the two cases: "Leopold is a truth-teller" or "Leopold is a liar". You can picture the reasoning process as a tree:
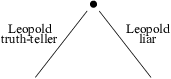
You can start with either case --- let's suppose you start with "Leopold is a truth-teller". (Note that this means anything he said is true.) Reason from this until you get a contradiction, a solution (that is, you know what all the characters are), or no conclusion.
I'll consider the first of these three cases in more detail, but similar ideas hold for the other two cases.
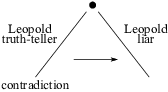
Thus, suppose "Leopold is a truth-teller" gives a contradiction. Then he can't be a truth-teller, so he must be a liar. The "Leopold is a truth-teller" branch of the tree is finished: Switch to the "Leopold is a liar" branch and start reasoning there.
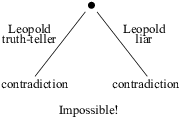
(a) If "Leopold is a liar" gives a contradiction, then both cases have given a contradiction and the original problem is impossible.
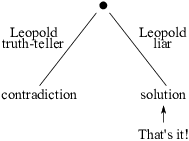
(b) If "Leopold is a liar" gives a solution, then that's the answer to the original problem.
(c) If "Leopold is a liar" gives no conclusion, then you need to take cases on another character. Let's say Molly is another character. Then we have the cases "Molly is a truth-teller" and "Molly is a liar", and they are sub-cases of "Leopold is a liar".

Now you have to continue reasoning with the two branches "Molly is a truth-teller" and "Molly is a liar".
If at some point all the branches end in contradictions, then the problem is impossible. If all the branches end in contradictions but one ends in a solution, then the solution is the answer to the problem. If more than one branch ends in a solution, the problem has multiple answers. If any of the branches ends in no conclusion, and you have no more characters with which to take cases, then again the problem has multiple answers.
Similar things would happen if our original choice ("Leopold is a truth-teller") gave a solution, or no conclusion.
It may also be that you should have started reasoning with another character --- so in the example I just went through, maybe you should have started by taking cases on Molly instead of Leopold. As with a lot of problem-solving and proof-writing, you should become accustomed to working on scratch paper and possibly throwing away early attempts in favor of later ones.
Example. You're on an island where each inhabitant is a truth-teller or a liar. Truth-tellers always tell the truth; liars always lie. Calvin and Phoebe are on the island.
Calvin says: "One or both of us is a liar."
Determine whether each person is a truth-teller or a liar.
Suppose Calvin is a liar. Then the statement "One or both of us is a liar" is true, contradicting the fact that Calvin is a liar.
Hence, Calvin is a truth-teller. Therefore, his statement is true, and at least one of them is a liar. Since it isn't Calvin, it must be Phoebe.
Thus, Calvin is a truth-teller and Phoebe is a liar.![]()
Here are other ideas for these kinds of problems.
1. If there are statements whose truth value you know (like "34 is odd"), begin with that information and see what you can conclude. For example, if Phoebe says "34 is odd", then (since the statement is false) I know Phoebe is a liar.
2. You must take cases in pairs, e.g. "Calvin is a liar" and "Calvin is a truth teller". And once you take cases, you must consider both.
3. Don't take cases unless you have to --- that is, unless you can't go any further with the information you know.
4. Observe that these solutions are written entirely in words: We aren't using truth tables here. You should avoid using symbols unless they are necessary. Mathematics does not necessarily require the use of symbols!
It's okay to use pictures (like the trees I drew above) to clarify your reasoning, but a picture is not a substitute for a verbal proof.
Example. You're on an island where each inhabitant is a truth-teller or a liar. Truth-tellers always tell the truth; liars always lie. Calvin and Phoebe are on the island.
Calvin says: "If I am a liar, then Phoebe is a liar."
Phoebe says: "Calvin is a truth-teller."
Determine whether each person is a truth-teller or a liar.
Suppose Calvin is a liar. Then his statement is false. Since it's an if-then statement, the if-part must be true and the then-part must be false. The if-part is "I am a liar", which is indeed true (by assumption). Then then-part must be false, so "Phoebe is a liar" is false, and hence Phoebe is a truth-teller. This means Phoebe's statement "Calvin is a truth-teller" is true, which contradicts our assumption that Calvin is a liar.
Since "Calvin is a liar" led to a contradiction, Calvin must be a truth-teller. Now Phoebe says "Calvin is a truth-teller", so she is telling the truth, and she is a truth-teller. Calvin's statement is "If I am a liar, then Phoebe is a liar". Both parts ("I am a liar" and "Phoebe is a liar") are false, so the if-then statement is true, consistent with Calvin being a truth-teller.
Since "Calvin is a liar" led to a contradiction and
"Calvin is a truth-teller" led to a solution (consistent
with both characters' statements), we find that Calvin is a
truth-teller and Phoebe is a truth-teller.![]()
I noted that it's possible that a problem like this can't be solved, for either of the following reasons:
(a) There isn't enough information to determine what all the characters are.
(b) The given situation is impossible: All the cases lead to contradictions.
See if you can come up with problems of these two types.
Truth-teller and liar problems (and more complicated variants) were popularized by the logician Raymond Smullyan, who wrote a number of books with problems like this (see [1], for example).
[1] Raymond Smullyan, What is the name of this book. New York: Dover Publications, 2011.
Copyright 2019 by Bruce Ikenaga