Binomial Coefficients

If n and k are integers, $n \ge 0$ , and $0 \le k \le n$ , then the binomial coefficient $\displaystyle {n \choose k}$ (read n-choose-k) is defined by

$${n \choose k} = \dfrac{n!}{k!\,(n - k)!}.$$

Why "n-choose-k"? Suppose you have n different objects. How many ways are there of choosing k of them (without worrying about the order of choice)?

The first object can be chosen in n ways. Then there are $n - 1$ objects left, so the second can be chosen in $n - 1$ ways. Then there are $n - 2$ objects left, so the third can be chosen in $n - 2$ ways. And so on. At the $k^{\rm th}$ choice, you have $n - k + 1$ objects to choose from. So the number of ways of choosing k objects in a particular order is

$$n \cdot (n - 1) \cdot (n - 2) \cdot \cdots \cdot (n - k + 1) = \dfrac{1 \cdot 2 \cdot \cdots \cdot n}{1 \cdot 2 \cdot \cdots \cdot (n - k)} = \dfrac{n!}{(n - k)!}.$$

However, since I don't care about the order in which I choose the k objects (only which k objects are chosen), I have to divide by the number of different orders in which I could have chosen the k objects. This is the number of permutations of k objects, which is $k!$ . Hence, the number of ways of choosing k objects from a set of n, without regard for order, is

$$\dfrac{1}{k!} \cdot \dfrac{n!}{(n - k)!} = \dfrac{n!}{k!\, (n - k)!} = {n \choose k}.$$

Example. Compute $\displaystyle {5 \choose 3}$ and $\displaystyle {{10} \choose {10}}$ .

$${5 \choose 3} = \dfrac{5!}{3!\,2!} = \dfrac{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5}{1 \cdot 2 \cdot 3 \cdot 1 \cdot 2} = \dfrac{4 \cdot 5}{1 \cdot 2} = 10.$$

$${{10} \choose {10}} = \dfrac{10!}{10!\,0!} = 1.\quad\halmos$$

Proposition. ( Properties of binomial coefficients)

(a) $\displaystyle {n \choose n} = {n \choose 0} = 1$ .

(b) $\displaystyle {n \choose k} = {n \choose {n - k}}$ .

(c) ( Pascal's triangle) $\displaystyle {{n + 1} \choose k} = {n \choose k} + {n \choose {k - 1}}$ .

The last property has the following pictorial interpretation.

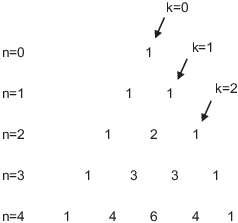
$$\hbox{\epsfysize=2in \epsffile{binomial-coefficients1.eps}}$$

Make a triangle as shown by starting at the top and writing 1's down the sides. Then fill in the middle of the triangle one row at a time, by adding the elements diagonally above the new element. For example, the leftmost 4 in the $n = 4$ row was obtained this way:

$$\matrix{ 1 & & & & 3 \cr & \searrow & & \swarrow & \cr & & 4 & & \cr}$$

The formula above is simply an algebraic expression of this addition procedure.

Proof. You can check the formulas in (a) and (b) by writing out the binomial coefficients. Here's the computation for one part of (a):

$${n \choose n} = \dfrac{n!}{n!\,0!} = 1.$$

And here's the computation for (b):

$${n \choose k} = \dfrac{n!}{k!\,(n - k)!} = \dfrac{n!}{(n - k)!\,k!} = {n \choose {n - k}}.$$

The proof of (c) is also a computation, though it's a little more involved:

$${n \choose k} + {n \choose {k-1}} = \dfrac{n!}{k!\,(n - k)!} + \dfrac{n!}{(k - 1)!\,(n - k + 1)!} = \dfrac{n!}{(k - 1)!\,(n - k)!} \left(\dfrac{1}{k} + \dfrac{1}{n - k + 1}\right) =$$

$$\dfrac{n!}{(k - 1)!\,(n - k)!} \cdot \dfrac{(n - k + 1) + k}{k(n - k + 1)} = \dfrac{n!}{(k - 1)!\,(n - k)!} \cdot \dfrac{n + 1}{k(n - k + 1)} = \dfrac{(n + 1)!}{k!\,(n - k + 1)!}.\quad\halmos$$

Of course, binomial coefficients get their name because they're the coefficients in the expansion of a binomial:

$$(x + y)^n = \sum_{k=0}^n {n \choose k} x^k y^{n - k}.$$

Since the coefficients can be read off from Pascal's triangle, you can use the triangle to write down binomial expansions.

Example. Use Pascal's triangle to compute the binomial expansion of $(x + y)^4$ .

Using the $n = 4$ row in the triangle, I get

$$(x + y)^4 = x^4 + 4 x^3 y + 6 x^2 y^2 + 4 x y^3 + y^4.\quad\halmos$$

Example. Determine the coefficient of $x^{37}y^3$ in the expansion of $(2x - 3y)^{40}$ .

The term containing $x^{37}y^3$ is

$${40 \choose 37}(2 x)^{37}(-3 y)^3 = \dfrac{40!}{37!\, 3!} 2^{37} (-3)^3 x^{37} y^3 = -38 \cdot 39 \cdot 40 \cdot 2^{36} \cdot 3^2 \cdot x^{37} y^3.$$

(I cancelled the $37!$ with the first 37 terms in $40!$ , then cancelled the $3! = 3 \cdot 2$ with $2^{37}$ and $3^3$ .) The coefficient is $-38 \cdot 39 \cdot 40 \cdot 2^{36} \cdot 3^2$ , or -36663215228190720 if you multiply it out.

Example. Prove that

$$\dfrac{4^n}{2 n + 1} < {{2 n} \choose n} \quad\hbox{for}\quad n \ge 1.$$

Some results involving binomial coefficients can be proven by choosing an appropriate binomial expansion. In this case, I notice that the "$2 n$ " in the binomial coefficient would come from expanding $(x + y)^{2 n}$ . But what should I choose for x and y?

After some trial and error, I find that this works:

$$4^n = 2^{2 n} = (1 + 1)^{2 n} = \sum_{k=0}^{2 n} {{2 n} \choose k} 1^k 1^{2 n - k} = \sum_{k=0}^{2 n} {{2 n} \choose k}.$$

The binomial coefficient $\displaystyle {{2 n} \choose n}$ is the middle term in this sum --- but being the middle term, it is also the largest term in the sum. Look at Pascal's Triangle to convince yourself that this is true:

$$\matrix{ & & & & 1 & & & & \cr & & & 1 & & 1 & & & \cr & & 1 & & 2 & & 1 & & \cr & 1 & & 3 & & 3 & & 1 & \cr 1 & & 4 & & 6 & & 4 & & 1 \cr}$$

There are $2 n + 1$ terms in the sum, and all of them are less than $\displaystyle {{2 n} \choose n}$ . Thus,

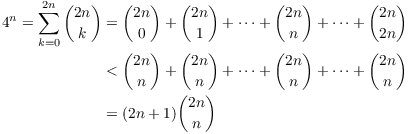
$$\eqalign{ 4^n = \sum_{k=0}^{2 n} {{2 n} \choose k} & = {{2 n} \choose 0} + {{2 n} \choose 1} + \cdots + {{2 n} \choose n} + \cdots + {{2 n} \choose {2 n}} \cr & < {{2 n} \choose n} + {{2 n} \choose n} + \cdots + {{2 n} \choose n} + \cdots + {{2 n} \choose n} \cr & = (2 n + 1) {{2 n} \choose n} \cr}$$

Dividing both sides by $2 n + 1$ , I get

$$\dfrac{4^n}{2 n + 1} < {{2 n} \choose n}.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga