Calendar Algorithms

Given a date in history, what day of the week was it?

First, some terminology. A sidereal year is the time is takes for the Earth to make 1 revolution around the sun relative to the fixed stars. It is approximately 365.25636 days.

The tropical year is the time it takes for the mean tropical longitude of the Sun to increase by 360 degrees. (Due to the increase in the Earth's precessional rate, the length of the tropical year decreases over time. A tropical year is approximately 365.24220 days.

The discrepancy between the sidereal year and the tropical year results from the precession of the Earth's axis of rotation: The Earth "wobbles" as it rotates. If no allowances were made for this, the seasons would occur at a slightly different time every year.

The Egyptian calendar had 365 days in a year. In 45 B.C., the Julian calendar was introduced. It had 365.25 days in a year, the year began in January (there being 12 months instead of the previous 10), and there was a leap year every 4-th year. This calendar loses approximately 1 day every 128 years.

By 1582, the calendar was nearly 11 days behind the calendar of 325 A.D. (Nicea). The vernal equinox, which now occurs around March 21, is the instant during spring when the sun "crosses" the Earth's equatorial plane. The vernal equinox had occurred around March 21 in the year 325; by the year 1582, it was occurring around March 11. The Gregorian calendar was introduced by Pope Gregory XIII in 1582. The ten days from October 4 through October 14 were dropped. (In other words, the day after October 4 was October 15.) The present leap year algorithm was introduced: A year divisible by 4 is a leap year, unless it's also divisible by 100, though years divisible by 400 are still leap years. Relative to the tropical year, this calendar loses around 1 day every 3300 years.

I'm going to account for the change from the Julian calendar to the Gregorian calendar later. First, I'll work out the day of the week for the Gregorian calendar in several steps.

Step 1 Find the day of the week of the first day of a given year.

It is convenient to have years "begin" on March 1. But so I don't get totally confused, whenever I write a date it will be understood to be the "standard" date. If I need to distinguish between a new date and a standard date, I'll use appropriate qualifiers.

I'll also use the following notation:

$$k = \hbox{day of the month}$$

$$m = \hbox{month}$$

$$N = 100C + Y, \quad\hbox{where}\quad C = \hbox{century} \quad\hbox{and}\quad Y = \hbox{year in the century}.$$

For instace, consider September 13, 1857. Then $k = 13$ , $m = 7$ (since March is 1), $C = 18$ , $Y = 57$ .

On the other hand, for January 3, 1954, I have $k = 3$ , $m = 11$ , $C = 19$ , $Y = 53$ . Note that 1953 has been redefined to run from the old March 1, 1953 to the old February 28, 1954.

The days of the week will be numbered beginning with Sunday:

$$\hbox{Sunday} = 0, \hbox{Monday} = 1, \ldots, \hbox{Saturday} = 6.$$

Remember that March 1 is now the first day of the year. Let

$$d_N = \hbox{day of the week of March 1 in the year N}.$$

For instance, in 1994, March 1 was a Tuesday, so $d_{1994} = 2$ .

If you know one value of $d_N$ , you can use it to get others. Note that

$$365 = 1 \mod{7} \quad\hbox{while}\quad 366 = 2 \mod{7}.$$

That is, $d_N$ increases by 1 over a normal year and by 2 over a leap year. So suppose I knew $d_{1600}$ . Then for $N \ge 1600$ ,

$$d_N = (N - 1600) + (\hbox{number of leap years, $1600 < x \le N$}) + d_{1600} \mod{7}.$$

The first term accounts for the one day contributed by every year, while the second term adds the extra day for each leap year. Note that since the year begins on March 1, this has to be interpreted correctly: the old 1992 was a leap year, but its extra day is contributed by the new 1991 (which extends through the old March 1, 1992).

There is a similar formula using any year besides 1600.

Example. Given that $d_{1994} = 2$ , what day of the week was March 1, 1997?

$1997 - 1994 = 3$ , and there is one intervening leap year. So

$$d_{1997} = 3 + 1 + d_{1994} = 6 \mod{7}.$$

So March 1, 1997 was a Saturday.

I'll go back to 1600 as my reference. I want to know how many leap years there were between 1600 and the year N, where $N \ge 1600$ . It's easy to count using the greatest integer function:

$$(\hbox{number of leap years, $1600 < x \le N$}) = \left[\dfrac{N - 1600}{4}\right] - \left[\dfrac{N - 1600}{100}\right] + \left[\dfrac{N - 1600}{400}\right] =$$

$$\left[\dfrac{N}{4} - 400\right] - \left[\dfrac{N}{100} - 16\right] + \left[\dfrac{N}{400} - 4\right].$$

Integers can be moved out of the greatest integer function, so I get

$$\left[\dfrac{N}{4}\right] - 400 - \left[\dfrac{N}{100}\right] + 16 + \left[\dfrac{N}{400}\right] - 4 = \left[\dfrac{N}{4}\right] - \left[\dfrac{N}{100}\right] + \left[\dfrac{N}{400}\right] - 388.$$

Now $N = 100 C + Y$ , so this becomes

$$\left[\dfrac{100 C + Y}{4}\right] - \left[\dfrac{100 C + Y}{100}\right] + \left[\dfrac{100 C + Y}{400}\right] - 388 = \left[25 C + \dfrac{Y}{4}\right] - \left[C + \dfrac{Y}{100}\right] + \left[\dfrac{C}{4} + \dfrac{Y}{400}\right] - 388.$$

$25 C$ and C are integers, and may be moved out of the greatest integer function. Since $0 \le Y < 100$ , $\dfrac{Y}{100} < 1$ , and $\left[\dfrac{Y}{100}\right] = 0$ . Moreover, $\dfrac{Y}{400} < \dfrac{1}{4}$ , and a little thought shows that this implies $\left[\dfrac{C}{4} + \dfrac{Y}{400}\right] = \left[\dfrac{C}{4}\right]$ . So I now have

$$\left[\dfrac{Y}{4}\right] + 25 C - C + \left[\dfrac{C}{4}\right] - 388 = 3 C + 4 + \left[\dfrac{C}{4}\right] + \left[\dfrac{Y}{4}\right] \mod{7}.$$

Plug this into the formula for $d_N$ :

$$d_N = (100 C + Y - 1600) + 3 C + 4 + \left[\dfrac{C}{4}\right] + \left[\dfrac{Y}{4}\right] + d_{1600} = d_{1600} + 5 C + Y + \left[\dfrac{C}{4}\right] + \left[\dfrac{Y}{4}\right] \mod{7}.$$

I can determine $d_{1600}$ by using $d_{1994} = 2$ :

$$2 = d_{1600} + 5 \cdot 19 + 94 + \left[\dfrac{19}{4}\right] + \left[\dfrac{94}{4}\right] = d_{1600} + 4 + 3 + 4 + 23 \mod{7}, \quad d_{1600} = 3 \mod{7}.$$

Thus, the formula is

$$d_n = 3 + 5 C + Y + \left[\dfrac{C}{4}\right] + \left[\dfrac{Y}{4}\right] \mod{7}.$$

Example. What day of the week was March 1, 1776?

$C = 17$ , $Y = 76$ , so

$$d_{1776} = 3 + 5\cdot 17 + 76 + \left[\dfrac{17}{4}\right] + \left[\dfrac{76}{4}\right] = 5 \mod{7}.$$

It was a Friday.

Step 2 Find the day of the week for the first day of an arbitrary month in an arbitrary year.

Since February is the last month by my month convention, I only need to worry about months with 30 or 31 days in counting from March 1. These are months 1 through 11. Notice that

$$30 = 2 \mod{7} \quad\hbox{and}\quad 31 = 3 \mod{7}.$$

Thus, a month with 30 days causes the day of the week of the first day to shift by 2, while a month with 31 days causes the day of the week of the first day to shift by 3. I need a formula to "correct" $d_N$ by the right amount for $m = 1, \ldots, 12$ . The following formula works:

$$d_N + [2.6 m - 0.2] - 2 \mod{7}, \hbox{ where } m = 1, \ldots, 12.$$

That is, at the beginning of month m, the day of the week has shifted by $[2.6 m - 0.2] - 2$ from $d_N$ .

Agustin Suarez [personal communication] pointed out that the numbers "2.6" and "0.2" can be found by fitting a line to the data. This method is called Zeller's congruence; it was discovered by Christian Zeller in 1882.

Example. Given that March 1, 1776 was a Friday, what day of the week was April 1, 1776? What day of the week was February 1, 1777?

March 1, 1776 was a Friday, so $d_{1776} = 5$ . Then for April 1, 1776, $m = 2$ (April), and

$$d_{1776} + [5.2 - 0.2] - 2 = 5 + 5 - 2 = 8 = 1 \mod{7}.$$

So April 1, 1776 was a Monday.

For February 1, 1777, I have

$$d_{1776} + [31.2 - 0.2] - 2 = 5 + 31 - 2 = 34 = 6.$$

It was a Saturday. (Note that the old February 1, 1777 is considered part of 1776 by my convention, so $m = 12$ .)

Step 3 Find the day of the week for an arbitrary day in history (by the Gregorian calendar).

Consider the day k of the month m in the year $N = 100 C + Y$ . The formula from Step 2 gives the day of the week for the first day of the month, i.e. for $k = 1$ . The shift from 1 to an arbitrary k is just $k - 1$ :

$$W = (k - 1) + d_N + [2.6 m - 0.2] - 2 = (k - 1) + 3 + 5 C + Y + \left[\dfrac{C}{4}\right] + \left[\dfrac{Y}{4}\right] + [2.6 m - 0.2] - 2 =$$

$$k + 5 C + Y + \left[\dfrac{C}{4}\right] + \left[\dfrac{Y}{4}\right] + [2.6 m - 0.2] \mod{7}.$$

Example. January 24, 1988 was a Super Bowl Sunday ... uh, was it really a Sunday?

Here $m = 11$ , $k = 24$ , $C = 19$ , $Y = 87$ . So

$$W = 24 + 95 + 87 + \left[\dfrac{19}{4}\right] + \left[\dfrac{87}{4}\right] + [28.6 - 0.2] = 0 \mod{7}.$$

It works! --- it was a Sunday! Isn't math wonderful!

Finally, I'll explain the correction you need for Julian dates. Please note that this is still a simplification, because different countries converted to the Gregorian calendar at different times. I'll only do the case for the 1582 correction. The procedure is:

1. Add 10 days to the Julian date.

2. Subtract one day for each century not divisible by 400 between the Julian date and October 15, 1582.

Here is the rationale. Without worrying about the centuries, the Julian and Gregorian calendars would be 10 days apart due to the 10 days that Pope Gregory removed: $G = J + 10$ . But the Julian calendar also gives a leap day to century years such as 1500, whereas $400 \notdiv 1500$ so 1500 is not a Gregorian leap year. Here's how this looks in a particular case:

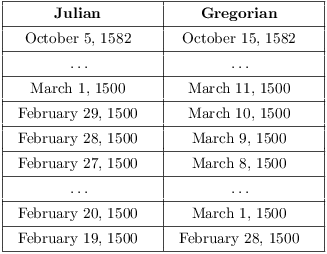
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & {\bf Julian} & & {\bf Gregorian} & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & October 5, 1582 & & October 15, 1582 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & \dots & & \dots & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & March 1, 1500 & & March 11, 1500 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & February 29, 1500 & & March 10, 1500 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & February 28, 1500 & & March 9, 1500 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & February 27, 1500 & & March 8, 1500 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & \dots & & \dots & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & February 20, 1500 & & March 1, 1500 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & February 19, 1500 & & February 28, 1500 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

Note that 1500 was a Julian leap year, but not a Gregorian leap year. As I move backwards through the leap day, the calendars go from being 10 days apart to being 9 days apart. That is, the Julian calendar gains a day on the Gregorian calendar for each such century leap year --- which explains the correction above.

Example. What day of the week was April 15, 1452 (the birthday of Leonardo da Vinci)?

This is prior to 1582, so I'll take it to be a Julian date. I add 10 days, then subtract one day for the single century date (1500) between 1452 and 1582 which is not divisible by 400. The corrected date is April 24, 1452. Thus, $k = 24$ , $m = 2$ , $C = 14$ , and $Y = 52$ :

$$W = 24 + 70 + 52 + \left[\dfrac{14}{4}\right] + \left[\dfrac{52}{4}\right] + [5.2 - 0.2] = 6 \mod{7}.$$

It was a Saturday.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga