Divisor Functions

Definition. The sum of divisors function is given by

$$\sigma(n) = \sum_{d \mid n} d.$$

As usual, the notation "$d \mid n$ " as the range for a sum or product means that d ranges over the positive divisors of n.

The number of divisors function is given by

$$\tau(n) = \sum_{d \mid n} 1.$$

For example, the positive divisors of 15 are 1, 3, 5, and 15. So

$$\sigma(15) = 1 + 3 + 5 + 15 = 24 \quad\hbox{and}\quad \tau(15) = 4.$$

I want to find formulas for $\sigma(n)$ and $\tau(n)$ in terms of the prime factorization of n. This will be easy if I can show that $\sigma$ and $\tau$ are multiplicative. I can do most of the work in the following theorem.

Theorem. The divisor sum of a multiplicative function is multiplicative.

Proof. Suppose f is multiplicative, and let $D(f)$ be the divisor sum of f. Suppose $(m, n) = 1$ . Then

$$[D(f)](m) = \sum_{a \mid m} f(a) \quad\hbox{and}\quad [D(f)](n) = \sum_{b \mid n} f(b).$$

Then

$$[D(f)](m)\cdot [D(f)](n) = \left(\sum_{a \mid m} f(a)\right) \left(\sum_{b \mid n} f(b)\right) = \sum_{a \mid m} \sum_{b \mid n} f(a)f(b).$$

Now $(m, n) = 1$ , so if $a \mid m$ and $b \mid n$ , then $(a, b) = 1$ . Therefore, multiplicativity of f implies

$$[D(f)](m) \cdot [D(f)](n) = \sum_{a \mid m} \sum_{b \mid n} f(a b).$$

Now every divisor d of $m n$ can be written as $d = a b$ , where $a \mid m$ and $b \mid n$ . Going the other way, if $a \mid m$ and $b \mid n$ then $a b \mid m n$ . So I may set $d = a b$ , where $d \mid m n$ , and replace the double sum with a single sum:

$$[D(f)](m) \cdot [D(f)](n) = \sum_{d \mid mn} f(d) = [D(f)](m n).$$

This proves that $D(f)$ is multiplicative.

Theorem. (a) The sum of divisors function $\sigma$ is multiplicative.

(b) The number of divisors function $\tau$ is multiplicative.

Proof. (a) The identity function $\id(x) = x$ is multiplicative: $\id(m n) = m n = \id(m) \cdot \id(n)$ for all m, n, so obviously it's true for $(m, n) = 1$ . Therefore, the divisor sum of $\id$ is multiplicative. But

$$[D(\id)](n) = \sum_{d \mid n} \id(d) = \sum_{d \mid n} d = \sigma(n).$$

Hence, the sum of divisors function $\sigma$ is multiplicative.

(b) The constant function $I(n) = 1$ is multiplicative: $I(m n) = 1 = 1 \cdot 1 = I(m) \cdot I(n)$ for all m, n, so obviously it's true for $(m, n) = 1$ . Therefore, the divisor sum of I is multiplicative. But

$$[D(I)](n) = \sum_{d \mid n} I(d) = \sum_{d \mid n} 1 = \tau(n).$$

Hence, the number of divisors function $\tau$ is multiplicative.

I'll use multiplicativity to obtain formulas for $\sigma(n)$ and $\tau(n)$ in terms of their prime factorizations (as I did with $\phi$ ). First, I'll get the formulas in the case where n is a power of a prime.

Lemma. Let p be prime.

(a) $\sigma(p^k) = \dfrac{p^{k+1} - 1}{p - 1}$ .

(b) $\tau(p^k) = k + 1$ .

Proof. The divisors of $p^k$ are 1, p, $p^2$ , ..., $p^k$ . So the sum of the divisors is

$$\sigma(p^k) = 1 + p + p^2 + \cdots + p^k = \dfrac{p^{k+1} - 1}{p - 1}.$$

And since the divisors of $p^k$ are 1, p, $p^2$ , ..., $p^k$ , there are $k + 1$ of them, and

$$\tau(p^k) = k + 1.\quad\halmos$$

Theorem. Let $n = p_1^{r_1}\cdots p_k^{r_k}$ , where the p's are distinct primes and $r_i \ge 1$ for all i. Then:

$$\sigma(n) = \left(\dfrac{p_1^{r_1+1} - 1}{p_1 - 1}\right)\cdots \left(\dfrac{p_k^{r_k+1} - 1}{p_k - 1}\right)$$

$$\tau(n) = (r_1 + 1)\cdots (r_k + 1)$$

Proof. These results follow from the preceding lemma, the fact that $\sigma$ and $\tau$ are multiplicative, and the fact that the prime power factors $p_i^{r_i}$ are pairwise relatively prime.

Here is a graph of $\sigma(n)$ for $1 \le n \le 1000$ .

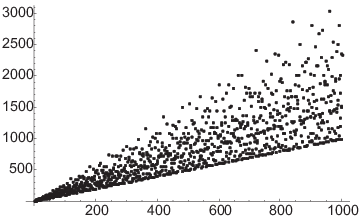
$$\hbox{\epsfysize=2in \epsffile{divisor-functions-1.eps}}$$

Note that if p is prime, $\sigma(p) = p + 1$ . This gives the point $(p, p + 1)$ , which lies on the line $y = x + 1$ . This is the line that you see bounding the dots below.

For each n, there are only finitely many numbers k whose divisor sum is equal to n: that is, such that $\sigma(k) = n$ . For k divides itself, so

$$n = \sigma(k) = (\hbox{other terms}) + k > k.$$

This says that k must be less than n. So if I'm looking for numbers whose divisors sum to n, I only need to look at numbers less than n. For example, if I want to find all numbers whose divisors sum to 42, I only need to look at $\{1, 2, \ldots, 41\}$ .

Here is a graph of $\tau(n)$ for $1 \le n \le 1000$ .

$$\hbox{\epsfysize=2in \epsffile{divisor-functions-2.eps}}$$

If p is prime, $\tau(p) = 2$ . Thus, $\tau$ repeatedly returns to the horizontal line $y = 2$ , which you can see bounding the dots below.

The formulas given in the theorem allow us to compute $\sigma(n)$ and $\tau(n)$ by hand for at least small values of n. For example, $720 = 2^4\cdot 3^2\cdot 5$ , so

$$\sigma(720) = \left(\dfrac{2^5 - 1}{2 - 1}\right) \left(\dfrac{3^3 - 1}{3 - 1}\right) \left(\dfrac{5^2 - 1}{5 - 1}\right) = 2418,$$

$$\tau(720) = (4 + 1)(2 + 1)(1 + 1) = 30.$$

Example. Find all positive integers n such that $\sigma(n) = n + 8$ .

Since $n = 1$ doesn't work, I can assume $n > 1$ .

I have

$$\eqalign{ n + 8 & = \sigma(n) = 1 + (\hbox{sum of divisors other than 1 and n}) + n \cr 7 & = (\hbox{sum of divisors other than 1 and n}) \cr}$$

In other words, $(\hbox{sum of divisors other than 1 and n})$ is a sum of distinct positive integers other than 1 and n that is equal to 7. I have to consider all possible ways of doing this. I'll consider cases according to the largest element of this sum, which is the largest divisor d of n other than 1 and n.

Suppose $d = 7$ .

$$(\hbox{sum of divisors other than 1 and n}) = 7.$$

Then the only divisor of n other than 1 and n is 7. Since $n \ne 7$ , I know $n = 7^k$ for $k > 1$ . But if $n > 49$ , then 49 would be a divisor of n other than 1 and n. Hence, $n = 49$ , and this is a solution.

Suppose $d = 6$ . Then the expression $(\hbox{sum of divisors other than 1 and n})$ must have the form $6 + 1$ , which contradicts the assumption that the sum does not include 1.

Suppose $d = 5$ . Then the expression $(\hbox{sum of divisors other than 1 and n})$ must have the form $2 + 5$ . In this case, $n = 2 \cdot 5 = 10$ .

Suppose $d = 4$ . Then

$$(\hbox{sum of divisors other than 1 and n}) = (\hbox{terms adding to 3}) + 4.$$

But if $4 \mid n$ , then $2 \mid n$ . So $(\hbox{terms adding to 3})$ must have the form $1 + 2$ , contradicting the assumption that the sum does not include 1.

Suppose $d = 3$ . Then

$$(\hbox{sum of divisors other than 1 and n}) = (\hbox{terms adding to 4}) + 3.$$

However, $(\hbox{terms adding to 4})$ can't include 1, and can't use 2 twice. Hence, this isn't possible.

Suppose $d = 2$ . Then the remaining terms in $(\hbox{sum of divisors other than 1 and n})$ must sum to 5 and can only use 1, which is excluded by assumption. Hence, this isn't possible.

Therefore, $n = 10$ or $n = 49$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga