Euler's Theorem

Euler's theorem generalizes Fermat's theorem to the case where the modulus is composite.

The key point of the proof of Fermat's theorem was that if p is prime, $\{1, 2, \ldots, p - 1\}$ are relatively prime to p.

This suggests that in the general case, it might be useful to look at the numbers less than the modulus n which are relatively prime to n. This motivates the following definition.

Definition. The Euler $\phi$ -function is the function on positive integers defined by

$$\phi(n) = (\hbox{the number of integers in $\{1, 2, \ldots, n - 1\}$ which are relatively prime to n}).$$

For example, $\phi(24) = 8$ , because there are eight positive integers less than 24 which are relatively prime to 24:

$$1, 5, 7, 11, 13, 17, 19, 23$$

On the other hand, $\phi(11) = 10$ , because all of the numbers in $\{1, \ldots, 10\}$ are relatively prime to 11.

Here is a graph of $(n,\phi(n))$ for $1 \le n \le 5000$ :

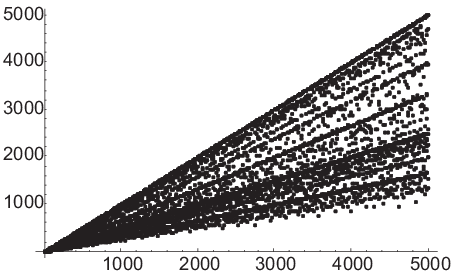
$$\hbox{\epsfysize=2.5in \epsffile{eulers-theorem-1.eps}}$$

You can see that the function jumps around a little, but the data points are bounded above by the line $y = x$ . A point will be nearly on this line whenever n is prime, and since there are infinitely many primes, there will always be points near it.

Later, I'll derive a formula for computing $\phi(n)$ in terms of the prime factorization of n.

Proposition.

(a) If p is prime, $\phi(p) = p - 1$ .

(b) If p is prime and $n \ge 1$ , then $\phi(p^n) = p^n - p^{n-1}$ .

(c) $\phi(n)$ counts the elements in $\{1, 2, \ldots, n - 1\}$ which are invertible mod n.

Proof. (a) If p is prime, then all of the numbers $\{1, \ldots, p - 1\}$ are relatively prime to p. Hence, $\phi(p) = p - 1$ .

(b) There are $p^n$ elements in $\{1, 2, \ldots, p^n\}$ . An element of this set is not relatively prime to p if and only if it's divisible by p. The elements of this set which are divisible by p are

$$1 \cdot p, \quad 2 \cdot p, \quad 3 \cdot p, \ldots, p^{n-1} \cdot p.$$

(Note that $p^{n-1} \cdot p = p^n$ is the last element of the set.) Thus, there are $p^{n-1}$ elements of the set which are divisible by p, i.e. $p^{n-1}$ elements of the set which are not relatively prime to p. Hence, there are $p^n - p^{n-1}$ elements of the set which are relatively prime to p.

(The definition of $\phi(p^n)$ applies to the set $\{1, 2, \ldots, p^n - 1\}$ , whereas I just counted the numbers from 1 to $p^n$ . But this isn't a problem, because I counted $p^n$ in the set, but then subtracted it off since it was not relatively prime to p.)

(c) $(a, n) = 1$ if and only if $a x = 1 \mod{n}$ for some x, so a is relatively prime to n if and only if a is invertible mod n. Now $\phi(n)$ is the number of elements in $\{1, 2, \ldots, n - 1\}$ which are relatively prime to n, so $\phi(n)$ is also the number of elements in $\{1, 2, \ldots, n - 1\}$ which are invertible mod n.

Definition. A reduced residue system mod n is a set of numbers

$$a_1, a_2, \ldots, a_{\phi(n)}$$

such that:

(a) If $i \ne j$ , then $a_i \ne a_j \mod{n}$ . That is, the a's are distinct mod n.

(b) For each i, $(a_i, n) = 1$ . That is, all the a's are relatively prime to n.

Thus, a reduced residue system contains exactly one representative for each number relatively prime to n. Compare this to a complete residue system mod n, which contains exactly one representative to every number mod n.

As an example, $\{1, 5, 7, 11\}$ is a reduced residue system mod 12. So is $\{-11, 17, 31, -1\}$ .

On the other hand, $\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11\}$ is a complete residue system mod 12.

Lemma. Let $\phi(n) = k$ , and let $\{a_1, \ldots, a_k\}$ be a reduced residue system mod n.

(a) For all m, $\{a_1 + mn , \ldots, a_k + m n\}$ is a reduced residue system mod n.

(b) If $(m, n) = 1$ , $\{m a_1, \ldots, m a_k\}$ is a reduced residue system mod n.

Proof. (a) This is clear, since $a_i = a_i + m n \mod{n}$ for all i.

(b) Since $(m, n) = 1$ , I may find x such that $m x = 1 \mod{n}$ . Since $(a_i, n) = 1$ , so I may find $b_i$ such that $a_i b_i = 1 \mod{n}$ . Then $(x b_i)(a m_i) = (m x)(a_i b_i) = 1 \mod{n}$ , which proves that $a m_i$ is invertible mod n. Hence, $(a m_i, n) = 1$ --- the $m a$ 's are relatively prime to n.

Now if $m a_i = m a_j \mod{n}$ , then $x m a_i = x m a_j \mod{n}$ , or $a_i = a_j \mod{n}$ . Since the a's were distinct mod n, this is only possible of $i = j$ . Hence, the $m a$ 's are also distinct mod n.

Therefore, $\{m a_1, \ldots, m a_k\}$ is a reduced residue system mod n.

Corollary. Let $\phi(n) = k$ , and let $\{a_1, \ldots, a_k\}$ be a reduced residue system mod n. Suppose $(s,n) = 1$ , and let t be any integer. Then the following is a reduced residue system mod n:

$$\{s a_1 + t n, s a_2 + t n, \ldots, s a_k + t n\} \quad\halmos$$

Here are some examples of these results. $\{1, 5\}$ is a reduced residue system mod 6. Adding $12 = 2 \cdot 6$ to each number, I get $\{13, 17\}$ , another reduced residue system mod 6.

Since $(6,25) = 1$ , I may multiply the original system by 25 to obtain $\{25, 125\}$ , another reduced residue system.

Finally, $\{25 + 12, 125 + 12\} = \{37, 137\}$ is yet another reduced residue system mod 12.

Theorem. (Euler) Let $n > 0$ , $(a, n) = 1$ . Then

$$a^{\phi(n)} = 1 \mod{n}.$$

Remark. If n is prime, then $\phi(n) = n - 1$ , and Euler's theorem says $a^{n - 1} = 1 \mod{n}$ , which is Fermat's theorem.

Proof. Let $\phi(n) = k$ , and let $\{a_1, \ldots, a_k\}$ be a reduced residue system mod n. I may assume that the $a_i$ 's lie in the range $\{1, \ldots, n - 1\}$ .

Since $(a, n) = 1$ , $\{a a_1, \ldots, a a_k\}$ is another reduced residue system mod n. Since this is the same set of numbers mod n as the original system, the two systems must have the same product mod n:

$$(a a_1)\cdots (a a_k) = a_1 \cdots a_k \mod{n}, \quad a^k (a_1 \cdots a_k) = a_1 \cdots a_k \mod{n}.$$

Now each $a_i$ is invertible mod n, so multiplying both sides by $a_1^{-1}\cdots a_k^{-1}$ , I get

$$a^k = 1 \mod{n}, \quad\hbox{or}\quad a^{\phi(n)} = 1 \mod{n}. \quad\halmos$$

As an example, $\phi(40) = 16$ , and $(9, 40) = 1$ . Hence, Euler's theorem says that $9^{16} = 1 \mod{40}$ .

Similarly, $21^{16} = 1 \mod{40}$ .

Example. Reduce $37^{103} \mod{40}$ to a number in the range $\{0, 1, \ldots 39\}$ .

Euler's theorem says that $37^{16} = 1 \mod{40}$ . So

$$37^{103} = 37^{96} \cdot 37^7 = (37^{16})^6 \cdot 94931877133 = 1 \cdot 13 = 13 \mod{40}.\quad\halmos$$

Example. Solve $15x = 7 \mod{32}$ .

Note that $(15,32) = 1$ and $\phi(32) = 16$ . Therefore, $15^{16} = 1 \mod{32}$ . Multiply the equation by $15^{15}$ :

$$x = 7 \cdot 15^{15} \mod{32}.$$

Now

$$7 \cdot 15^{15} = 105 \cdot 15^{14} = 105 \cdot (15^2)^7 = 105 \cdot 225^7 = 9 \cdot 1^7 = 9 \mod{32}.$$

So the solution is $x = 9 \mod{32}$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga