Fibonacci Numbers

The Fibonacci numbers are defined by the following recursive formula:

$$f_0 = 1, \quad f_1 = 1,$$

$$f_n = f_{n - 1} + f_{n - 2} \quad\hbox{for}\quad n \ge 2.$$

Thus, each number in the sequence (after the first two) is the sum of the previous two numbers.

(Some people start numbering the terms at 1, so $f_1 = 1$ , $f_2 = 1$ , and so on. But the recursion is the same.)

The first few Fibonacci numbers are:

$$1, \quad 1, \quad 2, \quad 3, \quad 5, \quad 8, \ldots .$$

Fibonacci numbers have been extensively studied. Koshy [1] and Rao [2] have extensive lists of Fibonacci identities; Koshy also has many applications. The Fibonacci Quarterly is a journal devoted to Fibonacci numbers and related topics.

Example. Express each of the following as a single Fibonacci number.

(a) $f_{5 n + 1} + f_{5 n + 2}$ .

(b) $f_{349} - f_{348}$ .

(c) $f_{2 n + 7} + f_{2 n + 4} + f_{2 n + 5}$ .

(a) The number after $5 n + 1$ and $5 n + 2$ is $5 n + 3$ , so

$$f_{5 n + 1} + f_{5 n + 2} = f_{5 n + 3}.\quad\halmos$$

(b) Since $f_{347} + f_{348} = f_{349}$ ,

$$f_{349} - f_{348} = f_{347}.\quad\halmos$$

(c)

$$f_{2 n + 7} + f_{2 n + 4} + f_{2 n + 5} = f_{2 n + 7} + f_{2 n + 6} = f_{2 n + 8}.\quad\halmos$$

Example. Prove that if $n \ge -1$ , then

$$f_{n + 5} + f_{n + 1} = 3 f_{n + 3}.$$

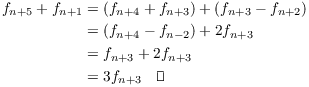
$$\eqalign{ f_{n + 5} + f_{n + 1} & = (f_{n + 4} + f_{n + 3}) + (f_{n + 3} - f_{n + 2}) \cr & = (f_{n + 4} - f_{n - 2}) + 2 f_{n + 3} \cr & = f_{n + 3} + 2 f_{n + 3} \cr & = 3 f_{n + 3} \quad\halmos \cr}$$

Many results about Fibonacci numbers can be proved by induction.

Example. Prove that

$$f_0 + f_1 + \cdots + f_n = f_{n + 2} - 1 \quad\hbox{for}\quad n \ge 0.$$

For $n = 0$ , the left side is $f_0 = 1$ and the right side is

$$f_2 - 1 = 2 - 1 = 1.$$

The result is true for $n = 0$ .

Suppose the result holds for n:

$$f_0 + f_1 + \cdots + f_n = f_{n + 2} - 1.$$

I'll prove it for $n + 1$ .

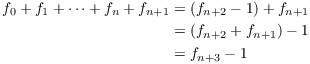
$$\eqalign{ f_0 + f_1 + \cdots + f_n + f_{n + 1} & = (f_{n + 2} - 1) + f_{n + 1} \cr & = (f_{n + 2} + f_{n + 1}) - 1 \cr & = f_{n + 3} - 1 \cr}$$

This proves the result for $n + 1$ , so the result is true for all $n \ge 0$ by induction.

Example. Prove that for $n \ge 0$ ,

$$f_n f_{n + 2} = f_{n + 1}^2 + (-1)^n.$$

For $n = 0$ , the left side is

$$f_0 f_2 = 1 \cdot 2 = 2.$$

The right side is

$$f_1^2 + (-1)^0 = 1^2 + 1 = 2.$$

The result is true for $n = 0$ .

Assume the result for n:

$$f_n f_{n + 2} = f_{n + 1}^2 + (-1)^n, \quad\hbox{so}\quad f_{n + 1}^2 = f_n f_{n + 2} - (-1)^n.$$

Prove the result for $n + 1$ :

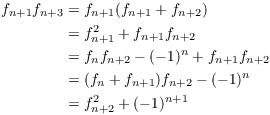
$$\eqalign{ f_{n + 1} f_{n + 3} & = f_{n + 1} (f_{n + 1} + f_{n + 2}) \cr & = f_{n + 1}^2 + f_{n + 1} f_{n + 2} \cr & = f_n f_{n + 2} - (-1)^n + f_{n + 1} f_{n + 2} \cr & = (f_n + f_{n + 1}) f_{n + 2} - (-1)^n \cr & = f_{n + 2}^2 + (-1)^{n + 1} \cr}$$

This proves the result for $n + 1$ , so it's true for $n \ge 0$ by induction.

Example. ( An explicit formula for the Fibonacci numbers)

(a) Let

$$\alpha = \dfrac{1 + \sqrt{5}}{2} \quad\hbox{and}\quad \beta = \dfrac{1 - \sqrt{5}}{2}.$$

Prove:

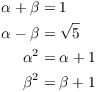
$$\eqalign{ \alpha + \beta & = 1 \cr \alpha - \beta & = \sqrt{5} \cr \alpha^2 & = \alpha + 1 \cr \beta^2 & = \beta + 1 \cr}$$

(b) Prove that

$$f_n = \dfrac{1}{\sqrt{5}} \alpha^{n+1} - \dfrac{1}{\sqrt{5}} \beta^{n+1} \quad\hbox{for}\quad n \ge 0.$$

(a)

$$\alpha + \beta = \dfrac{1 + \sqrt{5}}{2} + \dfrac{1 - \sqrt{5}}{2} = \dfrac{1 + \sqrt{5} + 1 - \sqrt{5}}{2} = \dfrac{2}{2} = 1.$$

$$\alpha - \beta = \dfrac{1 + \sqrt{5}}{2} - \dfrac{1 - \sqrt{5}}{2} = \dfrac{1 + \sqrt{5} - 1 + \sqrt{5}}{2} = \dfrac{2 \sqrt{5}}{2} = \sqrt{5}.$$

For the third and fourth equations, note that $\alpha$ and $\beta$ are roots of the quadratic equation

$$x^2 - x - 1 = 0.$$

So:

$$\alpha^2 - \alpha - 1 = 0 \quad\hbox{and hence}\quad \alpha^2 = \alpha + 1.$$

$$\beta^2 - \beta - 1 = 0 \quad\hbox{and hence}\quad \beta^2 = \beta + 1.$$

(b) For $n = 0$ , I have $f_0 = 1$ . The right side of the equation above becomes

$$\dfrac{1}{\sqrt{5}} \alpha - \dfrac{1}{\sqrt{5}} \beta = \dfrac{1}{\sqrt{5}} \cdot \sqrt{5} = 1.$$

The result is true for $n = 0$ .

For $n = 1$ , I have $f_1 = 1$ . The right side of the equation above becomes

$$\dfrac{1}{\sqrt{5}} \alpha^2 - \dfrac{1}{\sqrt{5}} \beta^2 = \dfrac{1}{\sqrt{5}} (\alpha^2 - \beta^2) = \dfrac{1}{\sqrt{5}} \left[(\alpha + 1) - (\beta + 1)\right] =$$

$$\dfrac{1}{\sqrt{5}} (\alpha - \beta) = \dfrac{1}{\sqrt{5}} \cdot \sqrt{5} = 1.$$

The result is true for $n = 1$ .

Assume that the result is true for all $k \le n$ . In particular,

$$f_n = \dfrac{1}{\sqrt{5}} \alpha^{n+1} - \dfrac{1}{\sqrt{5}} \beta^{n+1}.$$

$$f_{n - 1} = \dfrac{1}{\sqrt{5}} \alpha^n - \dfrac{1}{\sqrt{5}} \beta^n.$$

I'll prove the result for $n + 1$ .

$$f_{n + 1} = f_n + f_{n - 1} = \left(\dfrac{1}{\sqrt{5}} \alpha^{n+1} - \dfrac{1}{\sqrt{5}} \beta^{n+1}\right) + \left(\dfrac{1}{\sqrt{5}} \alpha^n - \dfrac{1}{\sqrt{5}} \beta^n\right) =$$

$$\dfrac{1}{\sqrt{5}} \left[\left(\alpha^{n + 1} + \alpha^n\right) + \left(\beta^{n + 1} + \beta^n\right)\right] = \dfrac{1}{\sqrt{5}} \left[\alpha^n (\alpha + 1) + \beta^n (\beta + 1)\right] =$$

$$\dfrac{1}{\sqrt{5}} \left(\alpha^n \cdot \alpha^2 + \beta^n \cdot \beta^2\right) = \dfrac{1}{\sqrt{5}} \left(\alpha^{n + 2} + \beta^{n + 2}\right).$$

This proves the result for $n + 1$ , so the result is true for all $n \ge 0$ by induction.

[1] Thomas Koshy, Fibonacci and Lucas Numbers with Applications. New York: John Wiley and Sons, 2001.

[2] K. Subba Rao, Some properties of Fibonacci numbers, American Mathematical Monthly, (10) 60 (1953), 680--684.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga