Fractions and Rational Numbers

Definition. A rational number is a real number which can be written as $\dfrac{a}{b}$ , where a and b are integers and $b \ne 0$ . A real number which is not rational is irrational.

Example. Prove that if p is prime, then $\sqrt{p}$ is irrational.

To prove this, suppose to the contrary that $\sqrt{p}$ is rational. Write $\sqrt{p} = \dfrac{a}{b}$ , where a and b are integers and $b \ne 0$ . I may assume that --- if not, divide out any common factors.

Now

$b \sqrt{p} = a \quad\hbox{so}\quad b^2p = a^2.$

Since $p \mid a^2$ and p is prime, $p \mid a$ . Write . Then

$b^2p = p^2 c^2, \quad\hbox{so}\quad b^2 = pc^2.$

Now $p \mid b^2$ , so $p \mid b$ . Thus, p is a common factor of a and b contradicting my assumption that .

It follows that $\sqrt{p}$ is irrational.

More generally, suppose , ..., $a_{n - 1}$ are integers and

$x^n + a_{n - 1} x^{n - 1} + \cdots + a_1 x + a_0.$

Then the roots are either integers or irrational.

If b is an integer such that , and a is a positive integer, then for some $n \ge 0$ I can write a uniquely in the form

$a = \sum_{i = 0}^n a_i b^i.$

This is called the base b expansion of a.

Note that

$a = a_n b^n + a_{n - 1} b^{n - 1} + \cdots + a_1 b + a_0.$

The notation is $(a_n\, a_{n - 1}\, \ldots a_1\, a_0)_b$ , with the subscript b denoting the base. We omit the subscript for number given in base-10.

Thus, the value of a is obtained by plugging into the polynomial

$a_n x^n + a_{n - 1} x^{n - 1} + \cdots + a_1 x + a_0.$

The standard way to do this by hand is to use synthetic division.

Example. Convert to base-10. Use synthetic division:

$\matrix{ 7 & 5 & 1 & 3 \cr \hphantom{-} & 56 & 488 & 3912 \cr \noalign{\vskip2pt \hrule \vskip2pt} 7 & 61 & 489 & 3915 \cr}$

Thus, .

To convert from base-10 to base-b, we just have to undo the process above. I divide the number by the base, noting the quotient and the remainder. Then I divide the quotient by the base, and so on. The successive remainders give the base-b digits (backwards).

Example. Convert 3915 to base-8. Divide 3915 by 8. The quotient is 489 and the remainder is 3:

$\matrix{ 489 & 3915 \cr \hphantom{-} & 3 \cr}$

Divide 489 by 8. The quotient is 61 and the remainder is 1:

$\matrix{ 61 & 489 & 3915 \cr \hphantom{-} & 1 & 3 \cr}$

Divide 61 by 8. The quotient is 7 and the remainder is 5:

$\matrix{ 7 & 61 & 489 & 3915 \cr \hphantom{-} & 5 & 1 & 3 \cr}$

Since 7 is less than 8, I can stop here. The answer is $(7\, 5\, 1\, 3)_8$ .

Note that if you want to convert between base-b and base-c, you could just do

$(\hbox{base-b}) \to (\hbox{base-10}) \to (\hbox{base-c})$

What about a positive number which is not an integer? I can write any positive real number as a sum of a positive integer and a real number between 0 and 1. I already know how to convert positive integers to base-b.

So suppose b is an integer such that , and a is a real number between 0 and 1 (inclusive). Then a can be written uniquely in the form

$a = \sum_{i = 1}^\infty a_i \cdot \dfrac{1}{b^i}.$

Rather than proving this fact, I'll merely recall the standard algorithm for computing such an expansion: Subtract from a as many $\dfrac{1}{b}$ 's as possible, subtract as many $\dfrac{1}{b^2}$ 's from what's left, and so on.

Here is a recursive procedure which generates base b expansions:

$a_i = \left[b \cdot x_{i-1}\right], \quad x_i = b \cdot x_{i-1} - \left[b \cdot x_{i-1}\right] \quad\hbox{for}\quad i \ge 1.$

To see why this corresponds to the standard algorithm, note that at the first stage I'm trying to find $k \ge 0$ such that

$a- \dfrac{k}{b} \ge 0 \quad\hbox{and}\quad a - \dfrac{k + 1}{b} < 0.$

These equations are equivalent to

$b a - k \ge 0 \quad\hbox{and}\quad b a - (k + 1) < 0.$

Equivalently,

$b a \ge k \quad\hbox{and}\quad b a < k + 1.$

That is, , and a corresponds to .

It's convenient to arrange the computations in a table, as shown below.

Example. Find 0.4 in base 7.

I fill in the rows from left to right. Starting with an x, multiply by to fill in the third column. Take the greatest integer of the result to fill in the a-column of the next row. Subtract the a-value from the last -value to get the next x, and continue. You can check that this is the algorithm described above.

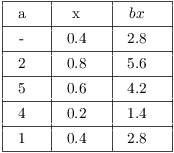
$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & a & & x & & $bx$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & - & & 0.4 & & 2.8 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 2 & & 0.8 & & 5.6 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 5 & & 0.6 & & 4.2 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 4 & & 0.2 & & 1.4 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 1 & & 0.4 & & 2.8 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

The expansion clearly repeats after this, since I'm getting 0.4 for x again. Thus,

$0.4 = (0.\overline{2541})_7.\quad\halmos$

Definition. The decimal expansion $x = .a_1a_2\ldots$ terminates if there is a number such that for .

In this case,

$x = \dfrac{a_1 \cdot 10^{n - 1} + a_2 \cdot 10^{n - 2} + \cdots + a_n}{10^n}.$

Hence, x is rational.

In fact, rational numbers in with terminating decimal are exactly the rational numbers of the form $\dfrac{p}{2^a 5^b}$ for and $a, b \ge 0$ .

Suppose a rational number has the form $\dfrac{p}{2^a 5^b}$ for and $a, b \ge 0$ . To see this, multiply the top and bottom by a power of 2 or a power of 5 to get a power of 10 on the bottom. Then $\dfrac{p}{2^a 5^b} = \dfrac{q}{10^c}$ , which is represented by a terminating decimal with q being the "decimal part". For example,

$\dfrac{17}{40} = \dfrac{17}{2^3 \cdot 5} = \dfrac{17 \cdot 5^2}{2^3 \cdot 5^3} = \dfrac{425}{10^3} = \dfrac{425}{1000} = 0.425.$

Going the other way, note that

$0.a_1\, a_2\, \ldots a_n = \dfrac{a_1 \cdot 10^n + a_2 \cdot 10^{n - 1} + \cdots a_n}{10^n} = \dfrac{a_1 \cdot 10^n + a_2 \cdot 10^{n - 1} + \cdots a_n}{2^n \cdot 5^n}.$

For instance,

$0.4173 = \dfrac{4173}{10000} = \dfrac{4 \cdot 10^3 + 1 \cdot 10^2 + 7 \cdot 10 + 3}{10^4} = \dfrac{4 \cdot 10^3 + 1 \cdot 10^2 + 7 \cdot 10 + 3}{2^4 \cdot 5^4}.$

Thus, a terminating decimal has the form $\dfrac{p}{2^a 5^b}$ for and $a, b \ge 0$ .

A decimal expansion $x = .a_1\, a_2\, \ldots$ is periodic with period k if there is a positive integer N such that $a_n = a_{n + k}$ for all $n \ge N$ .

Proposition. A periodic decimal expansion represents a rational number.

Proof. (Sketch) First consider the simplest case of a periodic decimal

$0.a_1\, a_2\, \ldots a_k\, a_1\, a_2\, \ldots a_k\, \ldots .$

This is a geometric series with first term $a = \dfrac{a_1 \cdot 10^{k - 1} + a_2 \cdot 10^{k - 2} + \cdots a_k}{10^k}$ and ratio $r = \dfrac{1}{10^k}$ .

a and r are both rational The sum of such a geometric series is $\dfrac{a}{1 - r}$ , which is also a rational number.

Suppose there is a pre-period --- an initial segment before the repeating part:

$x = 0.b_1\, b_2\, \ldots b_j\, a_1\, a_2\, \ldots a_k\, a_1\, a_2\, \ldots a_k\, \ldots .$

This is a sum of two rational numbers: The rational number corresponding to the terminating decimal $0.b_1\, b_2\, \ldots b_j$ and the rational number corresponding to the periodic part $a_1\, a_2\, \ldots a_k\, a_1\, a_2\, \ldots a_k\, \ldots$ , shifted by j places. Explicitly, if $a = \dfrac{a_1 \cdot 10^{k - 1} + a_2 \cdot 10^{k - 2} + \cdots a_k}{10^k}$ and $r = \dfrac{1}{10^k}$ , then

$x = \dfrac{b_1 \cdot 10^{j - 1} + b_2 \cdot 10^{j - 2} + \cdots b_j}{10^j} + \dfrac{1}{10^j} \cdot \dfrac{a}{1 - r}.$

Once again, this is rational.

Example. Express $0.\overline{473}$ as a rational number in lowest terms.

Since the number has period 3, I multiply both sides by :

$\eqalign{ x & = 0.\overline{473} = 0.473473 \ldots \cr 1000 x & = 473.473473 \ldots \cr}$

Next, subtract the first equation from the second:

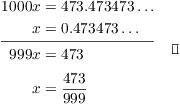
$\eqalign{ 1000 x & = 473.473473 \ldots \cr x & = 0.473473 \ldots \cr \noalign{\vskip2pt \hrule \vskip2pt} 999 x & = 473 \cr \noalign{\vskip2pt} x & = \dfrac{473}{999} \cr} \quad\halmos$

Example. Express $(0.24\overline{122})_{10}$ as a rational number in lowest terms.

Since the number has period 3, I multiply both sides by :

$\eqalign{ x & = (0.24\overline{122})_{10} = 0.24122122 \ldots \cr 1000 x & = 241.22122122 \ldots \cr}$

Next, subtract the first equation from the second:

$\eqalign{ 1000 x & = 241.22122122 \ldots \cr x & = 0.24122122 \ldots \cr \noalign{\vskip2pt \hrule \vskip2pt} 999 x & = 240.98 \cr x & = \dfrac{240.98}{999} = \dfrac{24098}{99900} = \dfrac{12049}{49950} \cr}\quad\halmos$

Example. Express $(0.\overline{473})_8$ as a base-10 rational number in lowest terms.

Since the number has period 3, I multiply both sides by :

$\eqalign{ x & = (0.\overline{473})_8 = (0.473473 \ldots)_8 \cr 512 \cdot x & = (473.473473 \ldots)_8 \cr}$

Next, subtract the first equation from the second, being careful about the bases: I have base-10 on the left, but base-8on the right.

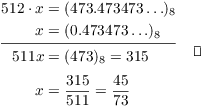
$\eqalign{ 512 \cdot x & = (473.473473 \ldots)_8 \cr x & = (0.473473 \ldots)_8 \cr \noalign{\vskip2pt \hrule \vskip2pt} 511 x & = (473)_8 = 315 \cr \noalign{\vskip2pt} x & = \dfrac{315}{511} = \dfrac{45}{73} \cr} \quad\halmos$

In the next two problems, I'll use the formula for the sum of a geometric series:

$a + a r + a r^2 + a r^3 + \cdots + a r^n + \cdots = \dfrac{a}{1 - r}.$

Example. Suppose b is an integer and . Express the following as a rational function of b:

$(0.13\, 13\, \overline{13} \ldots)_b.$

Using the formula for the sum of a geometric series, I have

$\eqalign{ (0.13\, 13\, \overline{13} \ldots)_b & = \dfrac{1}{b} + \dfrac{3}{b^2} + \dfrac{1}{b^3} + \dfrac{3}{b^4} + \dfrac{1}{b^5} + \dfrac{3}{b^6} + \cdots \cr \noalign{\vskip2pt} & = \dfrac{b + 3}{b^2} + \dfrac{b + 3}{b^4} + \dfrac{b + 3}{b^6} + \cdots \cr \noalign{\vskip2pt} & = \dfrac{\dfrac{b + 3}{b^2}}{1 - \dfrac{1}{b^2}} \cr \noalign{\vskip2pt} & = \dfrac{b + 3}{b^2 - 1} \cr} \quad\halmos$

Example. Suppose b is an integer and . Express the following as a rational function of b:

$(0.(b - 2) 1\, (b - 2) 1\, \overline{(b - 2) 1} \ldots)_b.$

Using the formula for the sum of a geometric series, I have

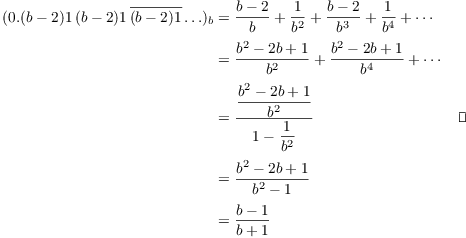
$\eqalign{ (0.(b - 2) 1\, (b - 2) 1\, \overline{(b - 2) 1} \ldots)_b & = \dfrac{b - 2}{b} + \dfrac{1}{b^2} + \dfrac{b - 2}{b^3} + \dfrac{1}{b^4} + \cdots \cr \noalign{\vskip2pt} & = \dfrac{b^2 - 2 b + 1}{b^2} + \dfrac{b^2 - 2 b + 1}{b^4} + \cdots \cr \noalign{\vskip2pt} & = \dfrac{\dfrac{b^2 - 2 b + 1}{b^2}}{1 - \dfrac{1}{b^2}} \cr \noalign{\vskip2pt} & = \dfrac{b^2 - 2 b + 1}{b^2 - 1} \cr \noalign{\vskip2pt} & = \dfrac{b - 1}{b + 1} \cr} \quad\halmos$

Proposition. A rational number can be represented by either a terminating decimal, or a periodic decimal.

Proof. (Sketch) Suppose $\dfrac{p}{q}$ is a rational number in lowest terms, so , and $0 < \dfrac{p}{q} < 1$ .

I've already shown that $\dfrac{p}{q}$ ca be represented by a terminating decimal if and only if for some $a, b \ge 0$ .

I'll consider the case where , so q is not divisible by 2 or by 5. By Euler's theorem,

$10^{\phi(q)} = 1 \mod{q}.$

Since some positive power of 10 is equal to 1 mod q, there must be a smallest positive power n such that $10^n = 1 \mod{q}$ . (This is called the order of 10 mod q.) Thus,

$10^n = m q + 1 \quad\hbox{for some}\quad m \in \integer^+.$

I have

$10^n \cdot \dfrac{p}{q} = \dfrac{(m q + 1) p}{q} = \dfrac{m q p}{q} + \dfrac{p}{q} = m p + \dfrac{p}{q}.$

On the other hand, I have the decimal expansion

$\dfrac{p}{q} = \dfrac{a_1}{10} + \dfrac{a_2}{10^2} + \cdots + \dfrac{a_n}{10^n} + x.$

Here x represents the remainder of the decimal expansion, so

$x = \dfrac{a_{n + 1}}{10^{n + 1}} + \dfrac{a_{n + 2}}{10^{n + 2}} + \dfrac{a_{n + 3}}{10^{n + 3}} + \cdots.$

Note that

$10^n x = \dfrac{a_{n + 1}}{10} + \dfrac{a_{n + 2}}{10^2} + \dfrac{a_{n + 3}}{10^3} + \cdots.$

Hence, .

So multiplying the equation for $\dfrac{p}{q}$ by , I get

$10^n \cdot \dfrac{p}{q} = \left(10^{n - 1} a_1 + 10^{n - 2} a_2 + \cdots + a_n\right) + 10^n x.$

Comparing the two equations for $10^n \cdot \dfrac{p}{q}$ , I have

$m p + \dfrac{p}{q} = \left(10^{n - 1} a_1 + 10^{n - 2} a_2 + \cdots + a_n\right) + 10^n x.$

I have an integer on either side, namely and $10^{n - 1} a_1 + 10^{n - 2} a_2 + \cdots + a_n$ . I also have on either side numbers in the range , namely $\dfrac{p}{q}$ and . This is only possible if $\dfrac{p}{q} = 10^n x$ . This means that at the $(n + 1)^{\rm st}$ place the decimal being constructed is the decimal for the original $\dfrac{p}{q}$ . Hence, the decimal must repeat after that point.

I'll omit the case where , where . In this case, the decimal has a pre-preriod before it begins to repeat.

For example, consider the rational fraction $\dfrac{10}{21}$ . I have $\phi(21) = 12$ , and checking powers I find that $10^6 = 1 \mod{21}$ , and this is the smallest positive power of 10 equal to 1 mod 21. Thus, I expect the decimal to have period 6. In fact,

$\dfrac{10}{21} = 0.809523\, 809523 \ldots .$

Contact information

Bruce Ikenaga's Home Page