The Fundamental Theorem of Arithmetic

Theorem. (Fundamental Theorem of Arithmetic) Every integer greater than 1 can be written in the form

$$p_1^{n_1} p_2^{n_2} \cdots p_k^{n_k}.$$

In this product, $n_i \ge 0$ and the $p_i$ 's are distinct primes. The factorization is unique, except possibly for the order of the factors.

For instance,

$$36 = 2^2 \cdot 3^2, \quad 4312 = 2^3 \cdot 7^2 \cdot 11, \quad 19 = 19^1.$$

I need a couple of lemmas in order to prove the uniqueness part of the Fundamental Theorem. In fact, these lemmas are useful in their own right.

Theorem. If $m \mid p q$ and $(m, p) = 1$ , then $m \mid q$ .

Proof. Write

$$1 = (m, p) = a m + b p \quad\hbox{for some}\quad a, b \in \integer.$$

Then

$$q = a m q + b p q.$$

Now $m \mid a m q$ and $m \mid b p q$ (since $m \mid p q$ ), so $m \mid (a m q + b p q) = q$ .

Theorem. If p is prime and $p \mid a_1 a_2 \cdots a_n$ , then $p \mid a_i$ for some i.

For $n = 2$ , the result says that if p is prime and $p \mid a b$ , then $p \mid a$ or $p \mid b$ . This is often called Euclid's lemma.

Proof. The result is trivial if $n = 1$ , since it says that if $p \mid a_1$ , then $p \mid a_1$ .

Do the case $n = 2$ first. Suppose $p \mid a_1 a_2$ , and suppose $p \notdiv a_1$ . I must show $p \mid a_2$ .

$(p, a_1) \mid p$ , and p is prime, so $(p, a_1) = 1$ or $(p, a_1) = p$ . If $(p, a_1) = p$ , then $p = (p, a_1) \mid a_1$ , which contradicts $p \notdiv a_1$ . Therefore, $(p, a_1) = 1$ . By the preceding theorem, $p \mid a_2$ . This establishes the result for $n = 2$ .

Assume $n > 2$ , and assume the result is true when p divides a product of with less than n factors. Suppose that $p \mid a_1a_2\cdots a_n$ . Grouping the terms, I have

$$p \mid (a_1 a_2 \cdots a_{n-1}) a_n.$$

By the case $n = 2$ , either $p \mid a_1 a_2 \cdots a_{n-1}$ or $p \mid a_n$ . If $p \mid a_n$ , I'm done. Otherwise, if $p \mid a_1 a_2 \cdots a_{n-1}$ , then p divides one of $a_1$ , $a_2$ , ..., $a_{n-1}$ , by induction. In either case, I've shown that p divides one of the $a_i$ 's, which completes the induction step and the proof.

Using these results, I'll prove the Fundamental Theorem of Arithmetic.

Proof. ( Fundamental Theorem of Arithmetic) First, I'll use induction to show that every integer greater than 1 can be expressed as a product of primes.

$n = 2$ is prime, so the result is true for $n = 2$ .

Suppose $n > 2$ , and assume every number less than n can be factored into a product of primes. If n is prime, I'm done. Otherwise, n is composite, so I can factor n as $n = ab$ , where $1 < a, b < n$ . By induction, a and b can be factored into primes. Then $n = ab$ shows that n can, too.

Now I'll prove the uniqueness part of the Fundamental Theorem.

Suppose that

$$p_1^{m_1} \cdots p_j^{m_j} = q_1^{n_1} \cdots q_k^{n_k}.$$

Here the p's are distinct primes, the q's are distinct primes, and all the exponents are greater than or equal to 1. I want to show that $j = k$ , and that each $p_a^{m_a}$ is $q_b^{n_b}$ for some b --- that is, $p_a = q_b$ and $m_a = n_b$ .

Consider $p_1$ . It divides the left side, so it divides the right side. By the last lemma, $p_1 \mid q_i^{n_i}$ for some i. But $q_i^{n_i}$ is $q_i \cdots q_i$ ($n_i$ times), so again by the last lemma, $p_1 \mid q_i$ . Since $p_1$ and $q_i$ are prime, $p_1 = q_i$ .

To avoid a mess, renumber the q's so $q_i$ becomes $q_1$ and vice versa. Thus, $p_1 = q_1$ , and the equation reads

$$p_1^{m_1} \cdots p_j^{m_j} = p_1^{n_1} \cdots q_k^{n_k}.$$

If $m_1 > n_1$ , cancel $p_1^{n_1}$ from both sides, leaving

$$p_1^{m_1-n_1} \cdots p_j^{m_j} = q_2^{n_2} \cdots q_k^{n_k}.$$

This is impossible, since now $p_1$ divides the left side, but not the right.

For the same reason $m_1 < n_1$ is impossible.

It follows that $m_1 = n_1$ . So I can cancel the $p_1$ 's off both sides, leaving

$$p_2^{m_2}\cdots p_j^{m_j} = q_2^{n_2}\cdots q_k^{n_k}.$$

Keep going. At each stage, I pair up a power of a p with a power of a q, and the preceding argument shows the powers are equal. I can't wind up with any primes left over at the end, or else I'd have a product of primes equal to 1. So everything must have paired up, and the original factorizations were the same (except possibly for the order of the factors).

Recall that the least common multiple of nonzero integers a and b is the smallest positive integer divisible by both a and b. The least common multiple of a and b is denoted $[a, b]$ .

For example,

$$[6, 4] = 12, \quad [33, 15] = 165.$$

Here's an interesting fact that is easy to derive from the Fundamental Theorem.

Proposition. If a and b are nonzero integers, then $[a, b](a, b) = ab $ .

Proof. (sketch) Factor a and b in products of primes, but write out all the powers (e.g. write $2^3$ as $2 \cdot 2 \cdot 2$ ):

$$a = p_1 \cdots p_l q_1 \cdots q_m, \quad b = q_1 \cdots q_m r_1 \cdots r_n.$$

Here the q's are the primes a and b have in common, and the p's and r don't overlap. Picture:

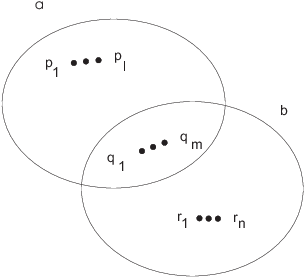
$$\hbox{\epsfysize=2.5in \epsffile{fundamental-theorem-1.eps}}$$

From the picture,

$$(a, b) = q_1 \cdots q_m, \quad [a, b] = p_1 \cdots p_l q_1 \cdots q_m r_1 \cdots r_n, \quad a b = p_1 \cdots p_l q_1^2 \cdots q_m^2 r_1 \cdots r_n.$$

Thus, $[a, b] (a, b) = a b$ .

You might see if you can prove this proposition without using the Fundamental Theorem (that is, without factoring a and b into products of primes.

Here's how this result looks for 36 and 90:

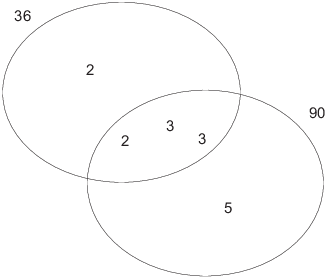
$$\hbox{\epsfysize=2.5in \epsffile{fundamental-theorem-2.eps}}$$

We have $(36, 90) = 18$ and $[36, 90] = 180$ ; notice that $36 \cdot 90 = 32400 = 18 \cdot 180$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga