The Greatest Integer Function

The following theorem is an extension of the Well-Ordering Axiom. It will be used to justify the definition of the greatest integer function

Theorem.

(a) Suppose S is a nonempty set of integers which is bounded below: There is an integer M such that $x > M$ for all $x \in S$ . Then S has a smallest element.

(b) Suppose S is a nonempty set of integers which is bounded above: There is an integer M such that $x < M$ for all $x \in S$ . Then S has a largest element.

Proof. (a) Suppose S is a nonempty set of integers, and $x > M$ for all $x \in S$ . I'll consider two cases.

First, if $M \ge 0$ , then $x > M \ge 0$ for all $x \in S$ . This shows that S is a subset of the positive integers, so it has a smallest element by the Well-Ordering Axiom.

Next, suppose $M < 0$ . In this case, the idea is to "translate" S to the right to get a subset of the positive integers to which Well-Ordering can be applied.

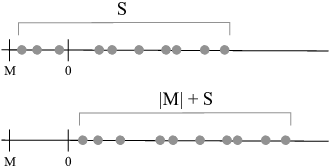
$$\hbox{\epsfysize=1.5in \epsffile{greatest-integer-function1.eps}}$$

Consider the set

$$|M| + S = \{x + |M| \mid x \in S\}.$$

If $x \in S$ , then

$$\eqalign{ x & > M \cr x + |M| & > M + |M| \ge 0 \cr}$$

This shows that the elements of $|M| + S$ are positive integers. By Well-Ordering, $|M| + S$ has a smallest element y. Thus, $y \in |M| + S$ , and $y \le x + |M|$ for all $x + |M| \in |M| + S$ .

Since $y \in |M| + S$ , I can write $y = z + |M|$ for some $z \in S$ .

Now if $x \in S$ , then

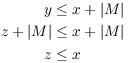
$$\eqalign{ y & \le x + |M| \cr z + |M| & \le x + |M| \cr z & \le x \cr}$$

Thus, z is an element of S which is at least as small as any other element of S --- that is, z is the smallest element of S.

(b) Suppose S is a nonempty set of integers and $x < M$ for all $x \in S$ . Then $-x > -M$ for all $x \in S$ , so the followng set is bounded below

$$-S = \{-x \mid x \in S\}.$$

By part (a), $-S$ has a smallest element. Suppose that y is the smallest element of $-S$ . Thus, $y \in -S$ , and $y \le -x$ for all $-x \in -S$ .

Since $y \in -S$ , I can write $y = -z$ , where $z \in S$ .

Now if $x \in S$ ,

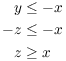
$$\eqalign{ y & \le -x \cr -z & \le -x \cr z & \ge x \cr}$$

Thus, z is an element of S which is at least as large as any other element of S --- that is, z is the largest element of S.

Definition. If x is a real number, then $[x]$ denotes the greatest integer function of x. It is the largest integer less than or equal to x.

It's probably obvious to you based on your experience with the real numbers that there is such an integer $[x]$ . You might find justifying this a bit of a challenge. Here's the idea.

For every real number x, the Archimedean Axiom for the real numbers says that there is an integer n such that $n > x$ .

Lemma. For every $x \in \real$ , there is an integer m such that $m < x$ .

Proof. Apply the Archimedean Axiom to $-x$ to get an integer n such that $n > -x$ . Negating the inequality, I get $-n < x$ . Then $-n$ is an integer less than x.

Now go back to the greatest integer function. Let $x \in \real$ . Why is there a largest integer less than or equal to x?

First, the lemma shows that there is an integer less than x, so the set S of integers less than or equal to x is nonempty.

Second, S is bounded above by x. By the Archimedean Axiom, there is an integer n such that $n > x$ . Then n is also an upper bound for S.

By part (b) of the theorem, S has a largest element. That element is $[x]$ .

That was a lot of work to show that the function $[x]$ is actually defined, particularly since this fact was probably obvious to you form the start!

When you learn about "ordinary" math like calculus, or number theory, you usually "start in the middle": A lot of things (that are hopefully plausible) are taken for granted. We don't normally go back to the very basic axioms, and perhaps this discussion helps you understand why we don't: We'd have to go through a lot of technicalities, and we wouldn't have the time to get to the ideas of calculus or number theory.

The following lemmas and examples should give you some ideas about how to work with the greatest integer function.

Example. Compute $[3.2]$ , $[117]$ , and $[-1.2]$

$$[3.2] = 3, \quad [117] = 117, \quad\hbox{and}\quad [-1.2] = -2.$$

(Notice that $[-1.2]$ is not equal to -1.)

Example. Sketch a graph of $f(x) = [x]$ .

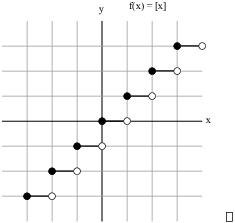
$$\hbox{\epsfysize=2in \epsffile{greatest-integer-function2.eps}}\quad\halmos$$

Lemma. If x is a real number, then

$$[x] + 1 > x \ge [x].$$

Proof. By definition, $x \ge [x]$ . To show that $[x] + 1 > x$ , I'll give a proof by contradiction.

Suppose on the contrary that $[x] + 1 \le x$ . Then $[x] + 1$ is an integer less than or equal to x, but $[x] + 1 > [x]$ --- which contradicts the fact that $[x]$ is the largest integer less than or equal to x. This contradiction implies that $[x] + 1 > x$ .

Lemma. If $x, y \in \real$ and $x \ge y$ , then $[x] \ge [y]$ .

Proof. Suppose $x \ge y$ . I want to show that $[x] \ge [y]$ .

Assume on the contrary that $[y] > [x]$ . Since $[x]$ is the {\it greatest} integer which is less than or equal to x, and since $[y]$ is an integer which is greater than $[x]$ , it follows that $[y]$ can't be less than or equal to x. Thus, $[y] > x$ . But $x \ge y$ , so $[y] > y$ , which is a contradiction.

Therefore, $[x] \ge [y]$ .

Example. Let x be a real number and let n be an integer. Prove that $[x + n] = [x] + n$ .

First, $x \ge [x]$ , so $x + n \ge [x] + n$ . Now $[x] + n$ is an integer less than or equal to $x + n$ , so it must be less than or equal to the greatest integer less than or equal to $x + n$ --- which is $[x + n]$ :

$$[x + n] \ge [x] + n.$$

Next, $x + n \ge [x + n]$ , so $x \ge [x + n] - n$ . $[x + n] - n$ is an integer less than or equal to x. Therefore, it must be less than or equal to the greatest integer less than or equal to x --- which is $[x]$ :

$$[x] \ge [x + n] - n.$$

Adding n to both sides gives

$$[x] + n \ge [x + n].$$

Since $[x + n] \ge [x] + n$ and $[x] + n \ge [x + n]$ , it follows that $[x] + n = [x + n]$ .

Example. Consider the sequence

$$\left[\sqrt{n} + \dfrac{1}{2}\right] \quad\hbox{for}\quad n \ge 1.$$

Show that it consists of two 1's, four 2's, six 3's, and so on:

$$1, \quad 1, \quad 2, \quad 2, \quad 2, \quad 2, \quad 3, \quad 3, \quad 3, \quad 3, \quad 3, \quad 3, \quad \ldots.$$

Note that for $k \ge 1$ , the expressions $\left(k + \dfrac{1}{2}\right)^2$ and $\left(k - \dfrac{1}{2}\right)^2$ are not integers. In addition,

$$\left(k + \dfrac{1}{2}\right)^2 - \left(k - \dfrac{1}{2}\right)^2 = \left(k^2 + k + \dfrac{1}{4}\right) - \left(k^2 - k + \dfrac{1}{4}\right) = 2 k.$$

Thus, the interval $\left[\left(k - \dfrac{1}{2}\right)^2, \left(k + \dfrac{1}{2}\right)^2\right]$ contains $2 k$ integers.

Now

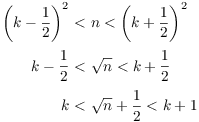
$$\eqalign{ \left(k - \dfrac{1}{2}\right)^2 < &\ n < \left(k + \dfrac{1}{2}\right)^2 \cr \noalign{\vskip2pt} k - \dfrac{1}{2} < &\ \sqrt{n} < k + \dfrac{1}{2} \cr \noalign{\vskip2pt} k < &\ \sqrt{n} + \dfrac{1}{2} < k + 1 \cr}$$

Hence, $\left[\sqrt{n} + \dfrac{1}{2}\right] = k$ .

That is, if n is one of the $2 k$ integers between $\left(k - \dfrac{1}{2}\right)^2$ and $\left(k + \dfrac{1}{2}\right)^2$ , the value of $\left[\sqrt{n} + \dfrac{1}{2}\right]$ is k. This shows that the given sequence consists of two 1's, four 2's, six 3's, and so on.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga