Infinite Continued Fractions

If $[a_0; a_1, a_2, \ldots]$ is an infinite continued fraction, I want to define its value to be the limit of the convergents:

$$\lim_{k \to \infty} c_k, \quad\hbox{where}\quad c_k \quad\hbox{is the k-th convergent}.$$

For this to make sense, I need to show that this limit exists.

In what follows, take as given an infinite continued fraction $[a_0; a_1, a_2, \ldots]$ . Let

$$p_0 = a_0, \quad q_0 = 1$$

$$p_1 = a_1 a_0 + 1, \quad q_1 = a_1$$

$$p_k = a_k p_{k - 1} + p_{k - 2}, \quad q_k = a_k q_{k - 1} + q_{k - 2}, \qquad k \ge 2,$$

$$c_k = \dfrac{p_k}{q_k}.$$

Proposition.

(a) $c_k - c_{k - 1} = \dfrac{(-1)^{k - 1}}{q_{k - 1} q_k}$ .

(b) $c_k - c_{k - 2} = \dfrac{a_k(-1)^k}{q_{k - 2} q_k}$ .

Proof. (a)

$$c_k - c_{k - 1} = \dfrac{p_k}{q_k} - \dfrac{p_{k - 1}}{q_{k - 1}} = \dfrac{p_k q_{k - 1} - p_{k - 1} q_k}{q_{k - 1} q_k} = \dfrac{(-1)^{k - 1}}{q_{k - 1} q_k}.$$

(b)

$$c_k - c_{k - 2} = \dfrac{p_k}{q_k} - \dfrac{p_{k - 2}}{q_{k - 2}} = \dfrac{p_k q_{k - 2} - p_{k - 2} q_k}{q_{k - 2}q_k} = \dfrac{(a_k p_{k - 1} + p_{k - 2}) q_{k - 2} - p_{k - 2} (a_k q_{k - 1} + q_{k - 2})}{q_{k - 2} q_k} =$$

$$\dfrac{a_k (p_{k - 1} q_{k - 2} - p_{k - 2} q_{k - 1})}{q_{k - 2} q_k} = \dfrac{a_k \cdot (-1)^{k - 2}}{q_{k - 2} q_k} = \dfrac{a_k (-1)^k}{q_{k - 2} q_k}.\quad\halmos$$

Proposition.

$$c_1 > c_3 > c_5 > \cdots > c_4 > c_2 > c_0.$$

That is, the odd convergents get smaller, the even convergents get bigger, and any odd convergent is bigger than any even convergent.

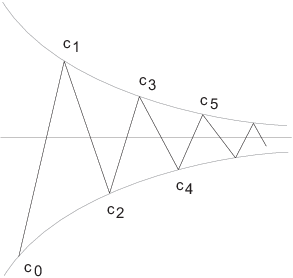
$$\hbox{\epsfysize=2.5in \epsffile{infinite-continued-fractions-1.eps}}$$

Proof. If k is even, then

$$c_k - c_{k - 2} = \dfrac{a_k(-1)^k}{q_{k - 2} q_k} > 0, \quad\hbox{so}\quad c_k > c_{k - 2}.$$

This shows that the even terms get bigger.

If k is odd, then

$$c_k - c_{k - 2} = \dfrac{a_k(-1)^k}{q_{k - 2} q_k} < 0, \quad\hbox{so}\quad c_k < c_{k - 2}.$$

This shows that the odd terms get smaller.

Finally, I have to show any odd term is bigger than any even term. Note that it's true if the terms are adjacent:

$$c_{2 n + 1} - c_{2 n} = \dfrac{(-1)^{(2 n + 1)-1}}{q_{k - 1}q_k} > 0, \quad\hbox{so}\quad c_{2 n + 1} > c_{2 n}.$$

Next, do the general case. Let $c_{2 n + 1}$ be an odd term and let $c_{2 m}$ be an even term. Then

$$c_{2 n + 1} > c_{2 n + 2 m + 1} > c_{2 n + 2 m} > c_{2 m}.$$

The first inequality is true because odd terms decrease. The second inequality is true because I just observed that an odd term is bigger than an adjacent even. Finally, the last inequality is true because even terms increase.

I've shown that any odd term is bigger than any even term, and that completes the proof.

Here's a numerical example. The first ten convergents for the golden ratio $\dfrac{1 + \sqrt{5}}{2}$ are

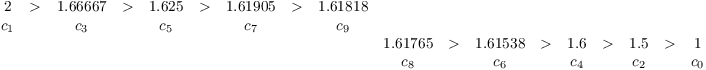
$$\matrix{ 2 & > & 1.66667 & > & 1.625 & > & 1.61905 & > & 1.61818 & & & & & & & & & \cr c_1 & & c_3 & & c_5 & & c_7 & & c_9 & & & & & & & & & \cr & & & & & & & & & 1.61765 & > & 1.61538 & > & 1.6 & > & 1.5 & > & 1 \cr & & & & & & & & & c_8 & & c_6 & & c_4 & & c_2 & & c_0 \cr}$$

The odd convergents get smaller, the even convergents get bigger, and any odd convergent is bigger than any even convergent.

Proposition. $q_k \ge k$ for all $k \ge 1$ .

Proof. I'll induct on k. $q_1 = a_1 \ge 1$ , so the result holds for $k = 1$ . Take $k > 1$ , and assume it holds for numbers less than or equal to k. I'll prove that it holds for $k + 1$ .

$$q_{k + 1} = a_{k + 1} q_k + q_{k - 1} \ge a_{k + 1} \cdot k + (k - 1) \ge 1 \cdot k + (k - 1) = 2 k - 1 = k + (k - 1) \ge k + 1.$$

(The last inequality used $k > 1$ .) This completes the induction step.

Theorem. Let $[a_0; a_1, a_2, \ldots]$ be an infinite continued fraction with $a_k > 0$ for $k \ge 1$ , and let $c_k$ be the k-th convergent. Then

$$\lim_{k \to \infty} c_k \quad\hbox{exists.}$$

Proof. Consider the sequence of odd convergents

$$c_1 > c_3 > c_5 > \cdots.$$

This is a decreasing sequence of numbers, and it's bounded below --- by any even convergent, for example. A standard result from analysis (see, for example, Theorem 3.14 of [1]) asserts that such a sequence must have a limit, so

$$\lim_{k \to \infty} c_{2 k + 1} \quad\hbox{exists}.$$

Likewise, consider the sequence of even convergents:

$$\cdots > c_4 > c_2 > c_0.$$

This is an increasing sequence of numbers that's bounded above --- by any odd convergent, for example. The result from analysis mentioned above says that the sequence has a limit:

$$\lim_{k \to \infty} c_{2 k} \quad\hbox{exists}.$$

I have to show that the two limits agree.

The previous result implies that $q_{2 k} \ge 2 k$ and $q_{2 k + 1} \ge 2 k + 1$ , so

$$0 \le c_{2 k + 1} - c_{2 k} = \dfrac{(-1)^{2 k + 1-1}}{q_{2 k} q_{2 k + 1}} \le \dfrac{1}{(2 k)(2 k + 1)}.$$

Now let $k \to \infty$ . $\dfrac{1}{(2 k)(2 k + 1)} \to 0$ , so by the Squeezing Theorem of calculus,

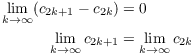
$$\eqalign{ \lim_{k \to \infty} (c_{2 k + 1} - c_{2 k}) & = 0 \cr \lim_{k \to \infty} c_{2 k + 1} & = \lim_{k \to \infty} c_{2 k} \cr}$$

Since the odd and even terms approach the same limit, $\displaystyle \lim_{k \to \infty} c_k$ exists.

Definition. $\displaystyle [a_0; a_1, a_2, \ldots] = \lim_{k \to \infty} c_k$ .

What can I say about the value of an infinite continued fraction?

Theorem. Let $[a_0; a_1, a_2, \ldots]$ be an infinite continued fraction with $a_k > 0$ for $k \ge 1$ . Then $[a_0; a_1, a_2, \ldots]$ is irrational.

Proof. Write $x = [a_0; a_1, a_2, \ldots]$ for short. I want to show that x is irrational. Suppose on the contrary that $x = \dfrac{p}{q}$ , where p and q are integers. I will show this leads to a contradiction.

Since the odd convergents are bigger than x and the even convergents are smaller than x,

$$c_{2 k + 1} > x > c_{2 k}.$$

Then

$$c_{2 k + 1} - c_{2 k} > x - c_{2 k} > 0,$$

$$\dfrac{(-1)^{2 k}}{q_{2 k} q_{2 k + 1}} > x - c_{2 k} > 0,$$

$$\dfrac{1}{q_{2 k} q_{2 k + 1}} > x - c_{2 k} > 0,$$

$$\dfrac{1}{q_{2 k}q_{2 k + 1}} > x - \dfrac{p_{2 k}}{q_{2 k}} > 0,$$

$$\dfrac{1}{q_{2 k + 1}} > x q_{2 k} - p_{2 k} > 0,$$

$$\dfrac{1}{q_{2 k + 1}} > \dfrac{p q_{2 k}}{q} - p_{2 k} > 0,$$

$$\dfrac{q}{q_{2 k + 1}} > p q_{2 k} - p_{2 k} q > 0.$$

Notice that this inequality is true for all k, and that $p q_{2 k} - p_{2 k} q$ is an integer. But q is fixed, and $q_{2 k + 1} \ge 2 k + 1$ , so if I make k sufficiently large eventually $q_{2 k + 1}$ will become bigger than q. Then $\dfrac{q}{q_{2 k + 1}}$ will be a fraction less than 1, and I have an integer $p q_{2 k} - p_{2 k} q$ caught between 0 and a fraction less than 1. Since this is impossible, x can't be rational.

Now I know that every infinite continued fraction made of positive integers represents an irrational number. The converse is also true, and it gives an algorithm for computing the continued fraction expansion.

Proposition Let $x \in \real$ be irrational. Let $x_0 = x$ , and

$$a_k = [x_k], \quad x_{k + 1} = \dfrac{1}{x_k - a_k} \quad\hbox{for}\quad k \ge 0.$$

Then for all $k \ge 0$ ,

$$x = [a_0; a_1, a_2, \ldots x_k] = a_0 + \dfrac{1}{a_1 + \dfrac{1}{\matrix{\noalign{\vskip2pt} \ddots & \cr & \dfrac{1}{a_{k - 1} + \dfrac{1}{x_k}}}}}$$

Thus, $x_k$ represents the "infinite tail" of the continued fraction.

Proof. For $k = 0$ , the claim is that $x = x_0$ , which is true by definition.

Assume that the result holds for n. Then

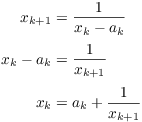
$$\eqalign{ x_{k + 1} & = \dfrac{1}{x_k - a_k} \cr \noalign{\vskip2pt} x_k - a_k & = \dfrac{1}{x_{k + 1}} \cr \noalign{\vskip2pt} x_k & = a_k + \dfrac{1}{x_{k + 1}} \cr}$$

Then

$$x = [a_0; a_1, a_2, \ldots x_k] = \left[a_0; a_1, a_2, \ldots a_k + \dfrac{1}{x_{k + 1}}\right] = [a_0; a_1, a_2, \ldots a_k, x_{k + 1}].$$

This proves the result for $k + 1$ , so the result is true for $k \ge 0$ by induction.

Theorem. Let $x \in \real$ be irrational. Let $x_0 = x$ , and

$$a_k = [x_k], \quad x_{k + 1} = \dfrac{1}{x_k - a_k} \quad\hbox{for}\quad k \ge 0.$$

Then

$$x = [a_0; a_1, a_2, \ldots].$$

Proof.

Step 1. $x_k$ is irrational for $k \ge 0$ .

Since x is irrational and $x_0 = x$ , the result is true for $k = 0$ .

Assume that $k > 0$ and that the result is true for $k - 1$ . I want to show that $x_k$ is irrational.

Suppose on the contrary that $x_k = \dfrac{s}{t}$ , where $s, t \in \integer$ . Then

$$\dfrac{s}{t} = \dfrac{1}{x_{k - 1} - a_{k - 1}} \quad\hbox{so}\quad x_{k - 1} = a_{k - 1} + \dfrac{t}{s}.$$

Now all the $a_k$ 's are clearly integers (since $a_k = [x_k]$ means they're outputs of the greatest integer function), so $a_{k - 1} + \dfrac{t}{s}$ is the sum of an integer and a rational number. Therefore, it's rational, so $x_{k - 1}$ is rational, contrary to the induction hypothesis.

It follows that $x_k$ is irrational. By induction, $x_k$ is irrational for all $k \ge 0$ .

Step 2. The $a_k$ 's are positive integers for $k \ge 1$ .

I already observed that the $a_k$ 's are integers.

Let $k \ge 0$ . Since $a_k = [x_k]$ , the definition of the greatest integer function gives

$$a_k \le x_k < a_k + 1.$$

But $x_k$ is irrational, so $a_k \ne x_k$ . Hence,

$$\eqalign{ a_k <\ & x_k < a_k + 1 \cr 0 <\ & x_k - a_k < 1 \cr \noalign{\vskip2pt} x_{k + 1} & = \dfrac{1}{x_k - a_k} > 1 \cr \noalign{\vskip2pt} a_{k + 1} & = [x_{k + 1}] \ge 1 \cr}$$

Since $k \ge 0$ , this proves that the $a_k$ 's are positive integers for $k \ge 1$ .

Step 3.

$$\lim_{k \to \infty} c_k = \lim_{k \to \infty} [a_0; a_1, \ldots, a_k] = x.$$

First, I'll get a formula for x in terms of the p's, q's, and a's.

Then I'll find $\left|x - \dfrac{p_k}{q_k}\right|$ and show that it's less than something which goes to 0.

Recall the recursion formulas for convergents:

$$p_k = a_k p_{k - 1} + p_{k - 2} \quad\hbox{and}\quad q_k = a_k q_{k - 1} + q_{k - 2}.$$

The right sides only involve terms up to $a_k$ (and p's and q's of smaller indices). Therefore, the following fractions have the same p's and q's through index k:

$$[a_0; a_1, a_2, \ldots, a_k, x_{k + 1}] \quad\hbox{and}\quad [a_0; a_1, a_2, \ldots, a_k, a_{k + 1}, \ldots].$$

Using the preceding proposition and the recursion formula for convergents, I get

$$x = x_0 = [a_0; a_1, a_2, \ldots, a_k, x_{k + 1}] = \dfrac{x_{k + 1} p_k + p_{k - 1}}{x_{k + 1} q_k + q_{k - 1}}.$$

Therefore,

$$x - \dfrac{p_k}{q_k} = \dfrac{x_{k + 1} p_k + p_{k - 1}}{x_{k + 1} q_k + q_{k - 1}} - \dfrac{p_k}{q_k} = \dfrac{x_{k + 1} p_k q_k + p_{k - 1} q_k - x_{k + 1} p_k q_k - p_k q_{k - 1}}{(x_{k + 1} q_k + q_{k - 1}) q_k} =$$

$$\dfrac{p_{k - 1} q_k - p_k q_{k - 1}}{(x_{k + 1} q_k + q_{k - 1}) q_k} = \dfrac{(-1)^k}{(x_{k + 1} q_k + q_{k - 1}) q_k}.$$

Take absolute values:

$$\left|x - \dfrac{p_k}{q_k}\right| = \dfrac{1}{(x_{k + 1} q_k + q_{k - 1}) q_k}.$$

Now

$$x_{k + 1} > [x_{k + 1}] = a_{k + 1}, \quad\hbox{so}\quad x_{k + 1} q_k + q_{k - 1} > a_{k + 1} q_k + q_{k - 1} = q_{k + 1}.$$

Therefore,

$$\dfrac{1}{x_{k + 1} q_k + q_{k - 1}} < \dfrac{1}{q_{k + 1}},$$

$$\dfrac{1}{(x_{k + 1}q_k + q_{k - 1}) q_k} < \dfrac{1}{q_{k + 1} q_k},$$

$$\left|x - \dfrac{p_k}{q_k}\right| < \dfrac{1}{q_{k + 1} q_k}.$$

By an earlier lemma, $q_k \ge k$ and $q_{k + 1} \ge k + 1$ , so

$$\left|x - \dfrac{p_k}{q_k}\right| < \dfrac{1}{q_{k + 1} q_k} \le \dfrac{1}{k (k + 1)}.$$

Now $\displaystyle \lim_{k \to \infty} \dfrac{1}{k (k + 1)} = 0$ , so by the Squeezing Theorem

$$\lim_{k \to \infty} \left|x - \dfrac{p_k}{q_k}\right| = 0.$$

This implies that

$$\lim_{k \to \infty} \dfrac{p_k}{q_k} = x.\quad\halmos$$

Example. Compute the first 5 terms of the continued fraction expansion of $\pi$ .

Here are the first two steps:

$$x_0 = \pi, \quad a_0 = [x_0] = [\pi] = 3$$

$$x_1 = \dfrac{1}{x_0 - a_0} \approx 7.06251, \quad a_1 = [x_1] = 7$$

Continuing in this way, I obtain:

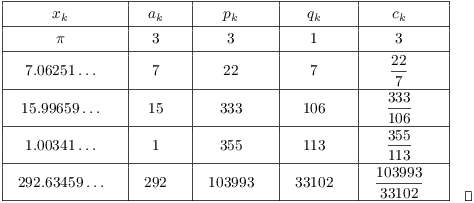
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x_k$ & & $a_k$ & & $p_k$ & & $q_k$ & & $c_k$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\pi$ & & 3 & & 3 & & 1 & & 3 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $7.06251 \ldots$ & & 7 & & 22 & & 7 & & $\dfrac{22}{7}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $15.99659 \ldots$ & & 15 & & 333 & & 106 & & $\dfrac{333}{106}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $1.00341 \ldots $ & & 1 & & 355 & & 113 & & $\dfrac{355}{113}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $292.63459 \ldots$ & & 292 & & 103993 & & 33102 & & $\dfrac{103993}{33102}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

Example. Compute the first 5 terms of the continued fraction expansion of $\sqrt{5}$ .

$$x_0 = \sqrt{5} \quad a_0 = [\sqrt{5}] \approx [2.23607] = 2$$

$$x_1 = \dfrac{1}{\sqrt{5} - 2}, \quad a_1 = \left[\dfrac{1}{\sqrt{5} - 2}\right] \approx [4.23607] = 4$$

Here are the first 5 terms:

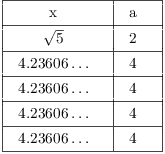
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & x & & a & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $\sqrt{5}$ & & 2 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $4.23606 \ldots$ & & 4 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $4.23606 \ldots$ & & 4 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $4.23606 \ldots$ & & 4 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $4.23606 \ldots$ & & 4 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

In fact, the continued fraction expansion for $\sqrt{5}$ is $[2; 4, 4, 4, \ldots]$ .

Theorem. The continued fraction expansion of an irrational number is unique.

Proof. Suppose there are two continued fractions for the irrational number x, where $a_k, b_k \in \integer$ and $a_k, b_k \ge 1$ for $k \ge 1$ :

$$[a_0; a_1, a_2, \ldots ] = x = [b_0; b_1, b_2, \ldots].$$

I want to show that $a_k = b_k$ for all k.

Recall that the even convergents are smaller than x and the odd convergents are greater than x.

Therefore,

$$a_0 < x < a_0 + \dfrac{1}{a_1}.$$

Now

$$\eqalign{ a_1 & \ge 1 \cr \noalign{\vskip2pt} \dfrac{1}{a_1} & \le 1 \cr \noalign{\vskip2pt} a_0 + \dfrac{1}{a_1} & \le a_0 + 1 \cr \noalign{\vskip2pt} x & < a_0 + 1 \cr}$$

Thus, $a_0$ is an integer less than x, and the next larger integer $a_0 + 1$ is greater than x. This means that $a_0 = [x]$ .

The same reasoning applies to the b's. Therefore, $b_0 = [x]$ , so $a_0 = b_0$ .

Hence,

$$\eqalign{ [a_0; a_1, a_2, \ldots] & = [b_0; b_1, b_2, \ldots] \cr \matrix{a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \vphantom{\dfrac{1}{a_3}}}} & & \cr & \ddots & \cr} & = \matrix{b_0 + \dfrac{1}{b_1 + \dfrac{1}{b_2 + \vphantom{\dfrac{1}{b_3}}}} & & \cr & \ddots & \cr} \cr \matrix{\dfrac{1}{a_1 + \dfrac{1}{a_2 + \vphantom{\dfrac{1}{a_3}}}} & & \cr & \ddots & \cr} & = \matrix{\dfrac{1}{b_1 + \dfrac{1}{b_2 + \vphantom{\dfrac{1}{b_3}}}} & & \cr & \ddots & \cr} \cr [a_1; a_2, a_3, \ldots] & = [b_1; b_2, b_3, \ldots] \cr}$$

I can continue in the same way to show that $a_k = b_k$ for all k.

Here's a summary of some of the important results on infinite continued fractions:

1. An irrational number has a unique infinite continued fraction expansion.

2. The algorithm for computing the continued fraction expansion of an irrational number x is:

$$x_0 = x, \quad\hbox{and}\quad a_k = [x_k], \quad x_{k + 1} = \dfrac{1}{x_k - a_k} \quad\hbox{for}\quad k \ge 1.$$

Then

$$x = [a_0; a_1, a_2, \ldots].$$

3. If $[a_0; a_1, a_2, \ldots]$ is the continued fraction expansion of an irrational number, then $a_0$ is an integer, and $a_k$ is a positive integer for $k \ge 1$ .

4. If $[a_0; a_1, a_2, \ldots]$ is a continued fraction expansion and $a_k > 0$ for $k \ge 1$ , then $[a_0; a_1, a_2, \ldots]$ is irrational.

5. If $x = [a_0; a_1, a_2, \ldots]$ is the continued fraction expansion of an irrational number and $\{p_k\}$ and $\{q_k\}$ are defined by the recursion formulas for convergents, then

$$\left|x - \dfrac{p_k}{q_k}\right| < \dfrac{1}{q_{k + 1} q_k}.$$

Example. Compute the first 6 convergents in the continued fraction expansion for $e + \pi$ .

Use them to illustrate the last result for $k = 4$ .

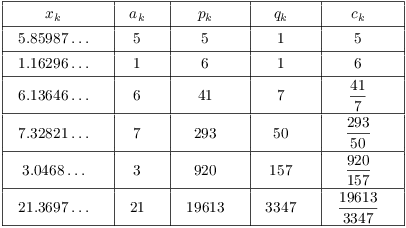
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x_k$ & & $a_k$ & & $p_k$ & & $q_k$ & & $c_k$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $5.85987 \ldots$ & & 5 & & 5 & & 1 & & 5 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $1.16296 \ldots$ & & 1 & & 6 & & 1 & & 6 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $6.13646 \ldots$ & & 6 & & 41 & & 7 & & $\dfrac{41}{7}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $7.32821 \ldots$ & & 7 & & 293 & & 50 & & $\dfrac{293}{50}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $3.0468 \ldots$ & & 3 & & 920 & & 157 & & $\dfrac{920}{157}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $21.3697 \ldots$ & & 21 & & 19613 & & 3347 & & $\dfrac{19613}{3347}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Now

$$e + \pi - \dfrac{920}{157} \approx 0.000001871 \quad\hbox{while}\quad \dfrac{1}{157\cdot 3347} \approx 0.000001903.$$

Thus, in this case,

$$\left|e + \pi - \dfrac{920}{157}\right| < \dfrac{1}{157 \cdot 3347}.\quad\halmos$$

[1] Walter Rudin, Principles of Mathematical Analysis ($3^{\rm rd}$ edition). New York: McGraw-Hill Book Company, 1976.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga