The Jacobi Symbol

It's a little inconvenient that the Legendre symbol $\legendre{a}{p}$ is only defined when the bottom is an odd prime. You can extend the definition to allow an odd positive number on the bottom using the Jacobi symbol. Most of the properties of Legendre symbols go through for Jacobi symbols, which makes Jacobi symbols very convenient for computation. We'll see, however, that there is a price to pay for the greater generality: Euler's formula no longer works, and we lose part of the connection between the value of a symbol and the solvability of the corresponding quadratic congruence.

Definition. Let $p, q \in \integer$ , where $(p, q) = 1$ and q is a product of odd primes:

$$q = q_1 q_2 \cdots q_n.$$

(The $q_i$ need not be distinct.) The Jacobi symbol $\legendre{p}{q}$ is defined by

$$\legendre{p}{q} = \legendre{p}{q_1} \legendre{p}{q_2} \cdots \legendre{p}{q_n}.$$

Note that the Jacobi symbol and the Legendre symbol coincide in the case where q is a single odd prime. That is why the same notation is used for both. It's clear from the definition that $\legendre{p}{q} = \pm 1$ .

Lemma. If q is a product of odd primes and a is a quadratic residue mod q, then $\legendre{a}{q} = 1$ .

Proof. Write $q = q_1 q_2 \cdots q_n$ , where each $q_i$ is an odd prime. Suppose a is a quadratic residue mod q. Then $(a, q) = 1$ and $x^2 = a \mod{q}$ has solutions.

Since $q_i \mid q$ , it follows that $(a, q_i) = 1$ and $x^2 = a \mod{q_i}$ for $i = 1, \ldots n$ . Hence, $\legendre{a}{q_i} = 1$ for $i = 1, \ldots n$ . Therefore,

$$\legendre{a}{q} = \legendre{a}{q_1} \legendre{a}{q_2} \cdots \legendre{a}{q_n} = 1 \cdot 1 \cdots 1 = 1.\quad\halmos$$

However, the converse is false: If $\legendre{p}{q}$ is a Jacobi symbol and $\legendre{p}{q} = 1$ , it does not follow that p is a quadratic reside mod q.

Example. Show that $\legendre{2}{15} = 1$ , but 2 is not a quadratic residue mod 15.

Since 2 is not a square mod 3 or mod 5,

$$\legendre{2}{3} = \legendre{2}{5} = -1.$$

Therefore,

$$\legendre{2}{15} = \legendre{2}{3} \legendre{2}{5} = (-1)(-1) = 1.$$

However, here is a table of squares mod 15:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & & 7 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 \mod{15}$ & & 0 & & 1 & & 4 & & 9 & & 1 & & 10 & & 6 & & 4 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 8 & & 9 & & 10 & & 11 & & 12 & & 13 & & 14 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 \mod{15}$ & & 4 & & 6 & & 10 & & 1 & & 9 & & 4 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The table shows that 2 is not a square mod 15. The quadratic residues mod 15 are 1 and 4, as those are the squares that are relatively prime to 15.

The results that follow amount to saying that the algebraic properties of Legendre symbols hold for Jacobi symbols --- and indeed, the proofs of these properties typically use those properties for Legendre symbols.

Theorem. Let q and $q'$ be odd positive numbers, and suppose $(p p', q q') = 1$ . Then:

(a) $\legendre{p}{q} \legendre{p}{q'} = \legendre{p}{q q'}$ .

(b) $\legendre{p}{q} \legendre{p'}{q} = \legendre{p p'}{q}$ .

(c) $\legendre{p^2}{q} = \legendre{p}{q^2} = 1$ .

(d) $\legendre{p^2 p'}{q^2 q'} = \legendre{p'}{q'}$ .

(e) If $p = p' \mod{q}$ , then $\legendre{p}{q} = \legendre{p'}{q}$ .

Proof. (a) Write q and $q'$ as products of odd primes:

$$q = q_1 q_2 \cdots q_m \quad\hbox{and}\quad q' = q_1' q_2' \cdots q_n'.$$

Then

$$\legendre{p}{q} \legendre{p}{q'} = \left(\legendre{p}{q_1} \legendre{p}{q_2} \cdots \legendre{p}{q_m}\right) \left(\legendre{p}{q_1'} \legendre{p}{q_2'} \cdots \legendre{p}{q_n'}\right) = \legendre{p}{q q'}.$$

(b) Write q as a product of odd primes:

$$q = q_1 q_2 \cdots q_m.$$

Then

$$\legendre{p}{q} \legendre{p'}{q} = \left(\legendre{p}{q_1} \legendre{p}{q_2} \cdots \legendre{p}{q_m}\right) \left(\legendre{p'}{q_1} \legendre{p'}{q_2} \cdots \legendre{p'}{q_m}\right) =$$

$$\left(\legendre{p}{q_1} \legendre{p'}{q_1}\right) \left(\legendre{p}{q_2} \legendre{p'}{q_2}\right) \cdots \left(\legendre{p}{q_m} \legendre{p'}{q_m}\right) = \legendre{p p'}{q_1} \legendre{p p'}{q_2} \cdots \legendre{p p'}{q_m} = \legendre{p p'}{q}.$$

(c) Write q as a product of odd primes:

$$q = q_1 q_2 \cdots q_m.$$

If $q_k$ is an odd prime, then $\legendre{p^2}{q_k} = 1$ (as a Legendre symbol). Hence,

$$\legendre{p^2}{q} = \legendre{p^2}{q_1} \legendre{p^2}{q_2} \cdots \legendre{p^2}{q_m} = 1 \cdot 1 \cdots 1 = 1.$$

Next, observe that if $q_k$ is an odd prime, then

$$\legendre{p}{q_k} \legendre{p}{q_k} = (\pm 1)^2 = 1.$$

So

$$\legendre{p}{q^2} = \legendre{p}{q_1} \legendre{p}{q_1} \legendre{p}{q_2} \legendre{p}{q_2} \cdots \legendre{p}{q_m} \legendre{p}{q_m} = 1 \cdot 1 \cdots 1 = 1.$$

(d)

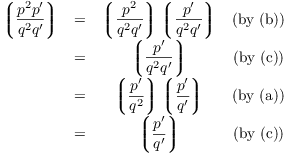
$$\matrix{ \legendre{p^2 p'}{q^2 q'} & = & \legendre{p^2}{q^2 q'} \legendre{p'}{q^2 q'} & (\hbox{by (b)}) \cr & = & \legendre{p'}{q^2 q'} & (\hbox{by (c)}) \cr & = & \legendre{p'}{q^2} \legendre{p'}{q'} & (\hbox{by (a)}) \cr & = & \legendre{p'}{q'} & (\hbox{by (c)}) \cr}$$

(e) Write q as a product of odd primes:

$$q = q_1 q_2 \cdots q_m.$$

Since $p = p' \mod{q}$ , I have $p = p' \mod{q_k}$ for $k = 1, \ldots m$ . Consequently, $\legendre{p}{q_k} = \legendre{p'}{q_k}$ (as Lengendre symbols). Therefore,

$$\legendre{p}{q} = \legendre{p}{q_1} \legendre{p}{q_2} \cdots \legendre{p}{q_m} = \legendre{p'}{q_1} \legendre{p'}{q_2} \cdots \legendre{p'}{q_m} = \legendre{p'}{q}.\quad\halmos$$

Example. Show that if $(a, q) = 1$ and q is odd and positive, it does not follow that

$$\legendre{a}{q} = a^{(q - 1)/2} \mod{q}.$$

(Thus, the analog of Euler's lemma does not hold for Jacobi symbols.)

Note that

$$\legendre{7}{15} = \legendre{7}{3} \legendre{7}{5} = \legendre{1}{3} \legendre{2}{5} = (1)(-1) = -1.$$

But

$$7^{(15 - 1)/2} = 7^7 = 13 \mod{15}.\quad\halmos$$

The next lemma will be used in the proofs of the formulas for $\legendre{-1}{q}$ and $\legendre{2}{q}$ , as well as in the proof that Quadratic Reciprocity holds for Jacobi symbols.

Lemma. If m and n are odd, then

$$\dfrac{m - 1}{2} + \dfrac{n - 1}{2} = \dfrac{m n - 1}{2} \mod{2}.$$

Proof. Since m and n are odd, I may write

$$m = 2 a + 1 \quad\hbox{and n = 2 b + 1}\quad\hbox{for}\quad a, b \in \integer.$$

Then

$$\dfrac{m - 1}{2} + \dfrac{n - 1}{2} = \dfrac{2 a + 1 - 1}{2} + \dfrac{2 b + 1 - 1}{2} = a + b.$$

On the other hand,

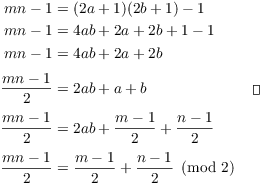
$$\eqalign{ m n - 1 & = (2 a + 1)(2 b + 1) - 1 \cr m n - 1 & = 4 a b + 2 a + 2 b + 1 - 1 \cr m n - 1 & = 4 a b + 2 a + 2 b \cr \noalign{\vskip2pt} \dfrac{m n - 1}{2} & = 2 a b + a + b \cr \noalign{\vskip2pt} \dfrac{m n - 1}{2} & = 2 a b + \dfrac{m - 1}{2} + \dfrac{n - 1}{2} \cr \noalign{\vskip2pt} \dfrac{m n - 1}{2} & = \dfrac{m - 1}{2} + \dfrac{n - 1}{2} \mod{2} \cr} \quad\halmos$$

Corollary. If $m_1, m_2, \ldots m_n$ are odd, then

$$\dfrac{m_1 - 1}{2} + \dfrac{m_2 - 1}{2} + \cdots + \dfrac{m_n - 1}{2} = \dfrac{m_1 m_2 \cdots m_n - 1}{2} \mod{2}.$$

Proof. Use the previous lemma and induction.

The way this corollary will be used in the following proof is the simple observation that if $s = t \mod{2}$ , then $(-1)^2 = (-1)^t$ .

Theorem. Let q be an odd positive number. Then

$$\legendre{-1}{q} = (-1)^{(q - 1)/2}.$$

Proof. Write q as a product of odd primes:

$$q = q_1 q_2 \cdots q_m.$$

Then

$$\legendre{-1}{q} = \legendre{-1}{q_1} \legendre{-1}{q_2} \cdots \legendre{-1}{q_n}.$$

The terms on the right are Legendre symbols, for which I know

$$\legendre{-1}{q_k} = (-1)^{(q_k - 1)/2} \quad\hbox{for}\quad k = 1, \ldots n.$$

Thus,

$$\legendre{-1}{q} = (-1)^{(q_1 - 1)/2} (-1)^{(q_2 - 1)/2} \cdots (-1)^{(q_n - 1)/2} = (-1)^S, \quad\hbox{where}\quad S = \sum_{k = 1}^n \dfrac{q_k - 1}{2}.$$

Using the preceding corollary,

$$S = \sum_{k = 1}^n \dfrac{q_k - 1}{2} = \dfrac{\prod_{k = 1}^n q_k - 1}{2} = \dfrac{q - 1}{2} \mod{2}.$$

Therefore,

$$\legendre{-1}{q} = (-1)^{(q - 1)/2}.\quad\halmos$$

Theorem. (Quadratic Reciprocity) Suppose p and q are odd positive integers and $(p, q) = 1$ . Then

$$\legendre{p}{q} \legendre{q}{p} = (-1)^{[(p - 1)/2] [(q - 1)/2]}.$$

Proof. I'll prove the equivalent statement

$$\legendre{p}{q} = \legendre{q}{p} \cdot (-1)^{[(p - 1)/2][(q - 1)/2]}.$$

(To get from either this statement to the original one or vice versa, multiply both sides by $\legendre{q}{p}$ and note that $\legendre{q}{p}^2 = 1$ .)

Write p and q as products of odd primes:

$$p = p_1 p_2 \cdot p_m \quad\hbox{and}\quad q = q_1 q_2 \cdots q_n.$$

Then

$$\legendre{p}{q} = \prod_{i = 1}^m \legendre{p_i}{q} = \prod_{i = 1}^m \prod_{j = 1}^n \legendre{p_i}{q_j}.$$

Here's what the last double product looks like, multiplied out:

$$\eqalign{ \legendre{p_1}{q_1} \legendre{p_2}{q_1} & \cdots \legendre{p_m}{q_1} \cdot \cr \legendre{p_1}{q_2} \legendre{p_2}{q_2} & \cdots \legendre{p_m}{q_2} \cdot \cr & \vdots \cr \legendre{p_1}{q_n} \legendre{p_2}{q_n} & \cdots \legendre{p_m}{q_n} \cr}$$

By Quadratic Reciprocity for Legendre symbols,

$$\legendre{p_i}{q_j} = \legendre{q_j}{p_i} (-1)^{[(p_i - 1)/2][(q_j - 1)/2]}.$$

Taking the product over i and j on both sides, I get

$$\legendre{p}{q} = \prod_{i = 1}^m \prod_{j = 1}^n \legendre{p_i}{q_j} = \prod_{i = 1}^m \prod_{j = 1}^n \legendre{q_j}{p_i} (-1)^{[(p_i - 1)/2][(q_j - 1)/2]} = \legendre{q}{p} \cdot \prod_{i = 1}^m \prod_{j = 1}^n (-1)^{[(p_i - 1)/2][(q_j - 1)/2]}.$$

Taking the product of powers of -1 causes the powers to add. So

$$\prod_{j = 1}^n (-1)^{[(p_i - 1)/2][(q_j - 1)/2]} = (-1)^S, \quad\hbox{where}\quad S = \sum_{i = 1}^m \sum_{j = 1}^n \dfrac{p_i - 1}{2} \cdot \dfrac{q_j - 1}{2}.$$

By the preceding corollary,

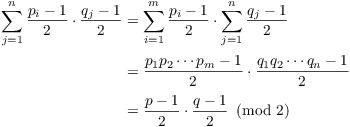
$$\eqalign{ \sum_{j = 1}^n \dfrac{p_i - 1}{2} \cdot \dfrac{q_j - 1}{2} & = \sum_{i = 1}^m \dfrac{p_i - 1}{2} \cdot \sum_{j = 1}^n \dfrac{q_j - 1}{2} \cr \noalign{\vskip2pt} & = \dfrac{p_1 p_2 \cdots p_m - 1}{2} \cdot \dfrac{q_1 q_2 \cdots q_n - 1}{2} \cr \noalign{\vskip2pt} & = \dfrac{p - 1}{2} \cdot \dfrac{q - 1}{2} \mod{2} \cr}$$

That is,

$$(-1)^S = (-1)^{[(p - 1)/2][(q - 1)/2]}.$$

Hence,

$$\legendre{p}{q} = \legendre{q}{p} \cdot (-1)^{[(p - 1)/2][(q - 1)/2]}.\quad\halmos$$

Remark. In computational terms, this version of reciprocity is like the one for Legendre symbols. Thus, suppose p and q are odd and relatively prime. If either p or q equals 1 mod 4, then

$$\legendre{p}{q} = \legendre{q}{p}.$$

If both p and q equal 3 mod 4, then

$$\legendre{p}{q} = -\legendre{q}{p}.$$

Next, I'll derive a formula for $\legendre{2}{q}$ , where q is an odd prime. The proof is similar to the proof of the formula for $\legendre{-1}{q}$ , except that I have slightly different preliminary lemmas.

Lemma. If m and n are odd, then

$$\dfrac{m^2 - 1}{8} + \dfrac{n^2 - 1}{8} = \dfrac{m^2 n^2 - 1}{8} \mod{2}.$$

Proof. Since m and n are odd, I may write

$$m = 2 a + 1 \quad\hbox{and n = 2 b + 1}\quad\hbox{for}\quad a, b \in \integer.$$

Then

$$\eqalign{ m^2 = 4 a^2 + 4 a + 1 & \quad\hbox{and}\quad n^2 = 4 b^2 + 4 b + 1 \cr m^2 - 1 = 4 a^2 + 4 a & \quad\hbox{and}\quad n^2 - 1 = 4 b^2 + 4 b \cr}$$

So

$$\dfrac{m^2 - 1}{8} + \dfrac{n^2 - 1}{8} = \dfrac{4 a^2 + 4 a}{8} + \dfrac{4 b^2 + 4 b}{8} = \dfrac{a^2 + a}{2} + \dfrac{b^2 + b}{2}.$$

(Note that $a^2 + a$ is even because it's the sum of two odd numbers, so $\dfrac{a^2 + a}{2}$ is an integer. Likewise, $\dfrac{b^2 + b}{2}$ is an integer.)

Now

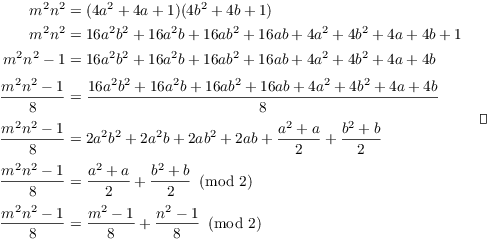
$$\eqalign{ m^2 n^2 & = (4 a^2 + 4 a + 1)(4 b^2 + 4 b + 1) \cr m^2 n^2 & = 16 a^2 b^2 + 16 a^2 b + 16 a b^2 + 16 a b + 4 a^2 + 4 b^2 + 4 a + 4 b + 1 \cr m^2 n^2 - 1 & = 16 a^2 b^2 + 16 a^2 b + 16 a b^2 + 16 a b + 4 a^2 + 4 b^2 + 4 a + 4 b \cr \noalign{\vskip2pt} \dfrac{m^2 n^2 - 1}{8} & = \dfrac{16 a^2 b^2 + 16 a^2 b + 16 a b^2 + 16 a b + 4 a^2 + 4 b^2 + 4 a + 4 b}{8} \cr \noalign{\vskip2pt} \dfrac{m^2 n^2 - 1}{8} & = 2 a^2 b^2 + 2 a^2 b + 2 a b^2 + 2 a b + \dfrac{a^2 + a}{2} + \dfrac{b^2 + b}{2} \cr \noalign{\vskip2pt} \dfrac{m^2 n^2 - 1}{8} & = \dfrac{a^2 + a}{2} + \dfrac{b^2 + b}{2} \mod{2} \cr \noalign{\vskip2pt} \dfrac{m^2 n^2 - 1}{8} & = \dfrac{m^2 - 1}{8} + \dfrac{n^2 - 1}{8} \mod{2} \cr} \quad\halmos$$

Corollary. If $m_1, m_2, \ldots m_n$ are odd, then

$$\dfrac{m_1^2 - 1}{8} + \dfrac{m_2^2 - 1}{8} + \cdots + \dfrac{m_n^2 - 1}{8} = \dfrac{m_1^2 m_2^2 \cdots m_n^2 - 1}{8} \mod{2}.$$

Proof. Use the previous lemma and induction.

Theorem. Let q be an odd positive number. Then

$$\legendre{2}{q} = (-1)^{(q^2 - 1)/8}.$$

Proof. Write q as a product of odd primes:

$$q = q_1 q_2 \cdots q_m.$$

Then

$$\legendre{2}{q} = \legendre{2}{q_1} \legendre{2}{q_2} \cdots \legendre{2}{q_n}.$$

The terms on the right are Legendre symbols, for which I know

$$\legendre{2}{q_k} = (-1)^{(q_k^2 - 1)/8} \quad\hbox{for}\quad k = 1, \ldots n.$$

Thus,

$$\legendre{2}{q} = (-1)^{(q_1^2 - 1)/8} (-1)^{(q_2^2 - 1)/8} \cdots (-1)^{(q_n^2 - 1)/8} = (-1)^S, \quad\hbox{where}\quad S = \sum_{k = 1}^n \dfrac{q_k^2 - 1}{8}.$$

Using the preceding corollary,

$$S = \sum_{k = 1}^n \dfrac{q_k^2 - 1}{8} = \dfrac{\prod_{k = 1}^n q_k^2 - 1}{8} = \dfrac{q^2 - 1}{8} \mod{2}.$$

Therefore,

$$\legendre{2}{q} = (-1)^{(q^2 - 1)/8}.\quad\halmos$$

Example. Compute the Jacobi symbol $\legendre{71}{375}$ .

$$\legendre{71}{375} = \legendre{71}{3 \cdot 5^3} = \legendre{71}{3 \cdot 5} = \legendre{71}{3} \legendre{71}{5} = \legendre{2}{3} \legendre{1}{5} = (-1)(1) = -1.\quad\halmos$$

Example. Compute the Legendre symbol $\legendre{91}{103}$ .

Jacobi symbols can often be used to simplify the computation of Legendre symbols.

$$\legendre{91}{103} = -\legendre{103}{91} = -\legendre{12}{91} = -\legendre{4 \cdot 3}{91} = -\legendre{3}{91} = -\legendre{3}{7 \cdot 13} =$$

$$-\legendre{3}{7} \legendre{3}{13} = -(-1) \legendre{7}{3} \legendre{13}{3} = \legendre{1}{3} \legendre{1}{3} = 1 \cdot 1 = 1.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga