Linear Congruences

Theorem. Let , and consider the equation

$a x = b \mod{m}.$

(a) If $d \notdiv b$ , there are no solutions.

(b) If $d \mid b$ , there are exactly d distinct solutions mod m.

Proof. Observe that

$a x = b \mod{m} \quad \Leftrightarrow \quad a x + m y = b \quad\hbox{for some}\quad y.$

Hence, (a) follows immediately from the corresponding result on linear Diophantine equations. The result on linear Diophantine equations which corresponds to (b) says that if is a particular solution, then there are infinitely many integer solutions

$x = x_0 + \dfrac{m}{d}t.$

I need to show that of these infinitely many solutions, there are exactly d distinct solutions mod m.

Suppose two solutions of this form are congruent mod m:

$x_0 + \dfrac{m}{d} t_1 = x_0 + \dfrac{m}{d} t_2 \mod{m}.$

Then

$\dfrac{m}{d} t_1 = \dfrac{m}{d} t_2 \mod{m}.$

Now $\dfrac{m}{d}$ divides both sides, and $\left(\dfrac{m}{d}, m\right) = \dfrac{m}{d}$ , so I can divide this congruence through by $\dfrac{m}{d}$ to obtain

$t_1 = t_2 \mod{d}.$

Going the other way, suppose $t_1 = t_2 \mod{d}$ . This means that and differ by a multiple of d:

$\dfrac{m}{d} t_1 - \dfrac{m}{d} t_2 = \dfrac{m}{d} \cdot k d = k m.$

This implies that

$\dfrac{m}{d} t_1 = \dfrac{m}{d} t_2 \mod{m}.$

$x_0 + \dfrac{m}{d} t_1 = x_0 + \dfrac{m}{d} t_2 \mod{m}.$

Let me summarize what I've just shown. I've proven that two solutions of the above form are equal mod m if and only if their parameter values are equal mod d. That is, if I let t range over a complete system of residues mod d, then $x_0 + \dfrac{m}{d} t$ ranges over all possible solutions mod m. To be very specific, all the solutions mod m are given by

$x_0 + \dfrac{m}{d} t \mod{m} \quad\hbox{for}\quad t = 0, 1, 2, \ldots, d - 1.\quad\halmos$

Example. Solve $6 x = 7 \mod{8}$ .

Since $(6,8) = 2 \notdiv 7$ , there are no solutions.

Example. Solve $3 x = 7 \mod{4}$ .

Since $(3,4) = 1 \mid 7$ , there will be 1 solutions mod 4. I'll find it in three different ways.

Using linear Diophantine equations.

$3 x = 7 \mod{4} \quad\hbox{implies}\quad 3 x + 4 y = 7 \quad\hbox{for some}\quad y.$

By inspection , is a particular solution. , so the general solution is

$x = 1 + 4 t, \quad y = 1 - 3 t.$

The y equation is irrelevant. The x equation says

$x = 1 \mod{4}.$

Using the Euclidean algorithm. Since , some linear combination of 3 and 4 is equal to 1. In fact,

$(-1) \cdot 3 + 1 \cdot 4 = 1.$

This tells me how to juggle the coefficient of x to get $1 \cdot x$ :

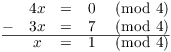
$\matrix{& 4 x & = & 0 & \mod{4} \cr - & 3 x & = & 7 & \mod{4} \cr \noalign{\hrule} & x & = & 1 & \mod{4} \cr}$

(I used the fact that $7 = -1 \mod{4}$ .

Using inverses mod 4. Here is a multiplication table mod 4:

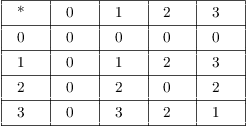
$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & * & & 0 & & 1 & & 2 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 0 & & 0 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & 1 & & 2 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 0 & & 2 & & 0 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 0 & & 3 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

I see that $3 \cdot 3 = 1 \mod{4}$ , so I multiply the equation by 3:

$3 x = 7 \mod{4}, \quad x = 21 = 1 \mod{4}.\quad\halmos$

Theorem. Let , and consider the equation

$a x + b y = c \mod{m}.$

(a) If $d \notdiv c$ , there are no solutions.

(b) If $d \mid c$ , there are exactly distinct solutions mod m.

I won't give the proof; it follows from the corresponding result on linear Diophantine equations.

Example. Solve

$2 x + 6 y = 4 \mod{10}.$

$(2, 6, 10) = 2 \mid 4$ , so there are $2 \cdot 10 = 20$ solutions mod 10. I'll solve the equation using a reduction trick similar to the one I used to solve two variable linear Diophantine equations.

The given equation is equivalent to

$2 x + 6 y + 10 z = 4 \quad\hbox{for some}\quad z.$

Set

$w = \dfrac{2}{(2, 6)} x + \dfrac{6}{(2, 6)} y.$

Then

$(2, 6) w + 10 z = 4, \quad 2 w + 10 z = 4, \quad w + 5 z = 2.$

, , is a particular solution. The general solution is

$w = -3 + 5 s, \quad z = 1 - s.$

Substitute for w:

$\dfrac{2}{(2, 6)} x + \dfrac{6}{(2, 6)} y = -3 + 5 s, \quad x + 3 y = -3 + 5 s.$

, , is a particular solution. The general solution is

$x = 5 s + 3 t, \quad y = -1 - t.$

$t = 0, 1, \ldots, 9$ will produce distinct values of y mod 10. Note, however, that s and produce and , which are congruent mod 10. That is, adding a multiple of 2 to a given value of s makes the term in x repeat itself mod 10. So I can get all possibilities for x mod 10 by letting .

All together, the distinct solutions mod 10 are

$x = 5 s + 3 t, \quad y = -1 - t, \quad \hbox{where} \quad s = 0, 1 \quad\hbox{and}\quad t = 0, 1, \ldots, 9.\quad\halmos$

Remarks: I saw the particular solution , by inspection. In general, you can get one using the Extended Euclidean algorithm. For example, in this case

$1 = (1, 3) = 1 \cdot (-2) + 3 \cdot 1.$

Multiply by (to match ) to get

$-3 + 5 s = 1 \cdot [-2 (-3 + 5 s)] + 3 \cdot (-3 + 5 s).$

So a particular solution is and .

In general, it can be tricky to determine the parameter ranges which give the correct number of solutions; it may require some trial-and-error, or careful analysis of the general solution.

Contact information

Bruce Ikenaga's Home Page