Modular Arithmetic

Definiton. Let a, b, and m be integers. $a = b\mod{m}$ (read "a equals b mod m" or a is congruent to b mod m) if any of the following equivalent conditions hold:

(a) $m \mid a - b$ .

(b) $m \mid b - a$ .

(d) (or ) for some $k \in \integer$ .

m is called the modulus of the congruence. I will almost always work with positive moduli.

Note that $a = 0 \mod{m}$ if and only if $m \mid a$ . Thus, modular arithmetic gives you another way of dealing with divisibility relations. Another way of saying this is: Mod m any multiple of m is 0.

Remark. Many people prefer to write " $a \equiv b \mod{m}$ ". Since equality mod m is an equivalence relation, since " " is a little less writing than " $\equiv$ ", and since there isn't much risk of confusion, I'll write " ".

Example.

(a) Reduce $101 \mod{3}$ to a number in the range $\{0, 1, 2\}$ .

(b) Reduce $-101 \mod{3}$ to a number in the range $\{0, 1, 2\}$ .

(a) $101 = 2 \mod{3}$ , because $3 \mid 101 - 2 = 99$ .

(b) $-101 = 1 \mod{3}$ , because $3 \mid -101 - 1 = -102$ .

Proposition. Congruence mod m is an equivalence relation:

(a) ( Reflexivity) $a = a\mod{m}$ for all a.

(b) ( Symmetry) If $a = b\mod{m}$ , then $b = a (\hbox{mod } m)$ .

Proof. I'll prove transitivity by way of example. Suppose $a = b \mod{m}$ and $b = c \mod{m}$ . Then there are integers j and k such that

$a - b = j m, \quad b - c = k m.$

Add the two equations:

This implies that $a = c \mod{m}$ .

Theorem. Suppose $a = b \mod{m}$ and $c = d \mod{m}$ . Then:

(a) $a + c = b + d \mod{m}$ .

(b) $a c = b d \mod{m}$ .

Note that you can use the second property and induction to show that if $a = b \mod{m}$ , then

$a^n = b^n \mod{m} \quad\hbox{for all}\quad n \ge 1.$

Proof. Suppose $a = b\mod{m}$ and $c = d\mod{m}$ .

(a) $m \mid a - b$ and $m \mid c - d$ , so by properties of divisibility,

$m \mid (a - b) + (c - d) = (a + c) - (b + d).$

This implies that $a + c = b + d \mod{m}$ .

(b) $m \mid a - b$ and $m \mid c - d$ imply that there are integers j and k such that

$a = b + m j \quad\hbox{and}\quad c = d + mk.$

Multiplying these two equations, I obtain

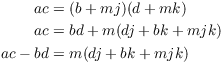
$\eqalign{ a c & = (b + m j)(d + m k) \cr a c & = b d + m(d j + b k + m j k) \cr a c - b d & = m(d j + b k + m j k) \cr}$

Hence, $m \mid a c - b d$ , so $a c = b d \mod{m}$ .

Corollary. Suppose $a = b \mod{m}$ . Then:

(a) $a \pm c = b \pm c \mod{m}$ .

(b) $a c = b c \mod{m}$ .

Proof. Apply the theorem to the equations $a = b \mod{m}$ and $c = c \mod{m}$ .

Assume that the modulus m is a positive integer. By the Division Algorithm, every integer n can be written as

$n = q m + r \quad\hbox{where}\quad 0 \le r < m.$

Reducing this equation mod m, I have $q m = 0 \mod{m}$ , so

$n = r \mod{m}.$

Since $0 \le r < m$ , I have $r \in \{0, 1, \ldots m - 1\}$ . In other words, mod m every integer can be reduced to a number in $\{0, 1, \ldots m - 1\}$ . This set is called the standard residue system mod m, and answers to modular arithmetic problems will usually be simplified to a number in this range.

Example. (a) What are the equivalence classes under the relation of congruence mod 3?

(b) Construct an addition table for addition mod 3.

(a) Consider congruence mod 3. There are 3 congruence classes:

$\{\ldots, -3, 0, 3, 6, \ldots\}, \quad \{\ldots -4, -1, 2, 5, \ldots\}, \quad \{\ldots -5, -2, 1, 4, \ldots\}.$

Each integer belongs to exactly one of these classes. Two integers in a given class are congruent mod 3.

(If you know some group theory, you probably recognize this as constructing $\integer_3$ from $\integer$ .)

(b) When you're doing things mod 3, it is if there were only 3 numbers. I'll grab one number from each of the classes to represent the classes; for simplicity, I'll use 0, 2, and 1.

Here is an addition table for the classes in terms of these representatives:

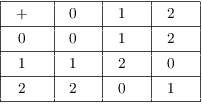
$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & + & & 0 & & 1 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 1 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 2 & & 0 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 0 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

Here's an example: , because as integers, and 3's congruence class is represented by 0. This is the table for addition mod 3.

I could have chosen different representatives for the classes --- say 3, -4, and 4, but I would have gotten an equivalent table. The simplest thing is to use the numbers $\{0, 1, 2\}$ from the standard residue system mod 3.

Example. ( Reducing an expression mod n) Reduce $100^5 \mod{7}$ to an element in the standard residue system $\{0, 1, \ldots, 6\}$ .

$100 = 2 \mod{7}$ , so

$100^5 = 2^5 = 32 = 4 \mod{7}.\quad\halmos$

Example. Simplify $994 \cdot 996 \cdot 997 \cdot 998 \mod{1000}$ to a number in the range $\{0, 1, \ldots 999\}$ .

Rather than deal with large "positive" numbers, I'll convert them to small "negative" numbers:

$994 = -6 \mod{1000}, \quad 996 = -4 \mod{1000}, \quad 997 = -3 \mod{1000}, \quad 998 = -2 \mod{1000}.$

$994 \cdot 996 \cdot 997 \cdot 998 = (-6)(-4)(-3)(-2) = 144 \mod{1000}.\quad\halmos$

Example. ( A modular binomial theorem) Prove that if p is prime, then

$(x + y)^p = x^p + y^p \mod{p}.$

By the Binomial Theorem,

$(x + y)^p = \sum_{i=0}^p {p \choose i} x^i y^{p-i}.$

A typical coefficient $\displaystyle {p \choose i} = \dfrac{p!}{i!\, (p - i)!}$ is divisible by p for $i \ne 0, p$ . So going mod p, the only terms that remain are and .

For example

$(x + y)^2 = x^2 + y^2 \mod{2} \quad\hbox{and}\quad (x + y)^3 = x^3 + y^3 \mod{3}.$

The result is not true if the modulus is not prime. For example,

$(1 + 1)^4 = 0 \mod{4}, \quad\hbox{but}\quad 1^4 + 1^4 = 2 \mod{4}.\quad\halmos$

Example. Prove that if $x \in \integer$ , then is not divisible by 5.

The phrase "not divisible by 5" leads one to think of doing things mod 5.

Every integer is equal to one of 0, 1, 2, 3, or 4 mod 5. Make a table:

$$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x \mod{5}$ & & 0 & & 1 & & 2 & & 3 & & 4 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $4 x^2 + x + 3 \mod{5}$ & & 3 & & 3 & & 1 & & 2 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$ From the table, $4 x^2 + x + 3 \ne 0 \mod{5}$ for all $x \in \integer$, so $5 \notdiv 4 x^2 + x + 3$ for all $x \in \integer$.\quad\halmos$

Example. Give a counterexample to show that $a = b \mod{n}$ does not imply that $x^a = x^b \mod{n}$ , for $a, b, n, x \in \integer$ .

For instance, $7 = 4 \mod{3}$ , but $2^7 \ne 2^4 \mod{3}$ (since $128 \ne 16 \mod{3}$ ).

Example. Solve the congruence

$6 x + 1 = 2(x + 2) \mod{7}.$

The modular arithmetic properties allow me to solve this equation the way I would solve a linear equation, up to a point. I multiply out the left side, then get the x's on one side:

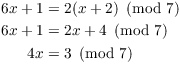
$\eqalign{ 6 x + 1 & = 2(x + 2) \mod{7} \cr 6 x + 1 & = 2 x + 4 \mod{7} \cr 4 x & = 3 \mod{7} \cr}$

If this were an equation over the real numbers, you could divide both sides by 4 --- equivalently, multiply both sides by $\dfrac{1}{4}$ .

What would " $\dfrac{1}{4}$ " mean mod 7? This is the multiplicative inverse of 4, which we write as $4^{-1}$ (in modular arithmetic you don't use fraction notation). This means: What number multiplied by 4 gives 1 mod 7?

Since there are only 7 numbers mod 7, I can do this by trial and error, multiplying 4 by 0, 1, ... until I get 1. I find that

$2 \cdot 4 = 8 = 1 \mod{7}.$

So for this modular equation, I multiply both sides by 2:

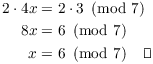
$\eqalign{ 2 \cdot 4 x & = 2 \cdot 3 \mod{7} \cr 8 x & = 6 \mod{7} \cr x & = 6 \mod{7} \quad\halmos \cr}$

You can see that finding multiplicative inverses mod n can be useful in solving congruences. Sometimes they can be found by more refined trial and error than simply trying all the numbers mod n.

Since multiples of n equal 0 mod n,

$1 = 1 + n = 1 + 2 n = 1 + 3 n = \cdots \mod{n}.$

I can sometimes use this to find inverses mod n.

Example.

(a) Use trial and error to find $5^{-1} \mod{7}$ .

(b) Use trial and error to find $45^{-1} \mod{89}$ .

(a) I take multiples of 7 and add 1, stopping when I get a number which is divisible by 5:

$7 + 1 = 8, \quad\hbox{but}\quad 5 \notdiv 8.$

$14 + 1 = 15. \quad\hbox{and}\quad 5 \mid 15.$

Since $3 \cdot 5 = 15$ , I have $5^{-1} = 3 \mod{7}$ .

(b) I take multiples of 89 and add 1, stopping when I get a number which is divisible by 45:

$89 + 1 = 90, \quad\hbox{and}\quad 45 \mid 90.$

Since $2 \cdot 45 = 90$ , I have $45^{-1} = 2 \mod{90}$ .

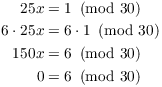
$\eqalign{ 25 x & = 1 \mod{30} \cr 6 \cdot 25 x & = 6 \cdot 1 \mod{30} \cr 150 x & = 6 \mod{30} \cr 0 & = 6 \mod{30} \cr}$

This contradiction shows that there is no such x, so 25 does not have a multiplicative inverse mod 30.

The previous method still has its limitations, as you can see by trying to use it to find $47^{-1} \mod{61}$ . And as you saw, some elements don't have multiplicative inverses mod n. The following theorem says which elements have multiplicative inverses, and how to find them if they exist.

Theorem. m has a multiplicative inverse mod n if and only if .

Proof. Suppose m has a multiplicative inverse mod n. This means that $a m = 1 \mod{n}$ for some a. Then

$a m + b n = 1 \quad\hbox{for some} \quad b \in \integer.$

Hence, .

Conversely, if , then

$a m + b n = 1 \quad\hbox{for some}\quad a, b \in \integer.$

Reducing mod n, I get $a m = 1 \mod{n}$ , which means that m has a multiplicative inverse mod n.

As the proof shows, you can find $a^{-1} \mod{n}$ by applying the Extended Euclidean algorithm to a and n.

Example. ( Finding elements which have multiplicative inverses) Which elements of $\{0, 1, 2, \ldots, 11\}$ have multiplicative inverses mod 12?

The numbers in $\{0, 1, 2, \ldots, 11\}$ which are relatively prime to 12 and 1, 5, 7, and 11. Hence, 1, 5, 7, and 11 have multiplicative inverses mod 12.

Example. Find $47^{-1} \mod{61}$ .

Apply the Extended Euclidean Algorithm to 61 and 47:

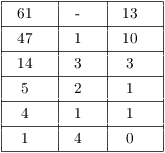
$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 61 & & - & & 13 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 47 & & 1 & & 10 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 14 & & 3 & & 3 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 5 & & 2 & & 1 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 4 & & 1 & & 1 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 1 & & 4 & & 0 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

Write the linear combination, then reduce mod 61:

$\eqalign{ (-10) \cdot 61 + 13 \cdot 47 & = 1 \cr 13 \cdot 47 & = 1 \mod{61} \cr}$

Hence, $47^{-1} = 13 \mod{61}$ .

Proposition. If $a c = b c\mod{m}$ , then

$a = b \mod{\dfrac{m}{(c, m)}}.$

Proof. Write

$a c - b c = k m, \quad\hbox{where}\quad k \in \integer.$

Then

$(a - b)\dfrac{c}{(c, m)} = k \dfrac{m}{(c, m)}.$

(Notice that $\dfrac{c}{(c, m)}$ and $\dfrac{m}{(c, m)}$ are integers, since $(c, m) \mid c$ and $(c, m) \mid m$ .) Now $\dfrac{c}{(c, m)}$ divides the right side, but it's relatively prime to $\dfrac{m}{(c, m)}$ . Therefore, it must divide k:

$k = \dfrac{c}{(c, m)} j \quad\hbox{for some}\quad j \in \integer.$

Hence,

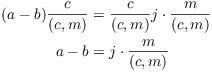
$\eqalign{ (a - b)\dfrac{c}{(c, m)} & = \dfrac{c}{(c, m)}j \cdot \dfrac{m}{(c, m)} \cr a - b & = j \cdot \dfrac{m}{(c, m)} \cr}$

Therefore, $a = b \mod{\dfrac{m}{(c, m)}}$ .

Notice that you "divide the equality" by c, but you divide the modulus by .

Example. ( Solving a congruence with cancellation) Solve

$12 x = 30 \mod{38}.$

$\eqalign{ 12 x & = 30 \mod{38} \cr 6 \cdot 2 x & = 6 \cdot 5 \mod{38} \cr}$

By the previous result, if I "cancel" the factors of 6, I must divide the modulus by . This makes the modulus 19:

$\eqalign{ 6 \cdot 2 x & = 6 \cdot 5 \mod{38} \cr 2 x & = 5 \mod{19} \cr}$

Now , so I can solve this congruence by multiplying by $2^{-1} \mod{19}$ . Noting that $2 \cdot 10 = 10 = 1 \mod{19}$ , I see that I need to multiply by 10:

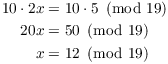
$\eqalign{ 10 \cdot 2 x & = 10 \cdot 5 \mod{19} \cr 20 x & = 50 \mod{19} \cr x & = 12 \mod{19} \cr}$

(If you didn't see that $2^{-1} = 10 \mod{19}$ by trial, you'd use the Extended Euclidean algorithm as before.)

The original congruence was mod 38, so I want all solutions in the range $\{0, 1, \ldots 37$ . I have one: . To get others, I add multiples of 19 until I exceed 37. Thus, is the other solution.

All together, the solutions are $x = 12 \mod{38}$ and $x = 31 \mod{38}$ .

Example. ( A congruence with no solutions) Show that the following congruence has no solutions:

$4 x = 5 \mod{14}.$

Suppose that x is a solution. Multiply the equation by 7:

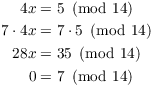
$\eqalign{ 4 x & = 5 \mod{14} \cr 7 \cdot 4 x & = 7 \cdot 5 \mod{14} \cr 28 x & = 35 \mod{14} \cr 0 & = 7 \mod{14} \cr}$

This contradiction shows that the equation has no solutions.

These examples show that linear congruences may have solutions or may be unsolvable. We can understand better what is happening by relating them to linear Diophantine equations.

Contact information

Bruce Ikenaga's Home Page