Perfect Numbers and Mersenne Primes

Definition. A number $n > 0$ is perfect if $\sigma(n) = 2 n$ . Equivalently, n is perfect if it is equal to the sum of its divisors other than itself.

Example. Show that 6 and 28 are perfect.

6 is perfect, because

$$6 = 1 + 2 + 3, \quad\hbox{or}\quad 2 \cdot 6 = 1 + 2 + 3 + 6.$$

28 is perfect, because

$$28 = 1 + 2 + 4 + 7 + 14, or 2 \cdot 28 = 1 + 2 + 4 + 7 + 14 + 28.\quad\halmos$$

It is not known whether there are any odd perfect numbers, or whether there are infinitely many even perfect numbers. The existence of infinitely many even perfect numbers is related to the existence of infinitely many Mersenne primes by the following result. One implication is in Euclid's Elements, and the other implication is due to Euler.

Theorem. n is an even perfect number if and only if $n = 2^a (2^{a + 1} - 1)$ , where $2^{a + 1} - 1$ is a Mersenne prime.

Proof. Here are some preliminaries before I start the proof. If n is an even integer, write $n = 2^a m$ , where $2 \notdiv m$ and $a > 1$ . Then

$$\sigma(n) = (2^{a + 1} - 1) \sigma(m).$$

I'll use this notation in both parts of the proof.

Suppose that n is perfect, so $\sigma(n) = 2 n$ .

Write

$$\eqalign{ s & = \sigma(m) - m \cr t & = 2^{a + 1} - 1 \cr}$$

Note that s is the sum of the divisors of m other than m. Note also that $t > 1$ , since $a > 1$ .

Then

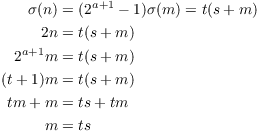
$$\eqalign{ \sigma(n) & = (2^{a + 1} - 1) \sigma(m) = t (s + m) \cr 2 n & = t (s + m) \cr 2^{a + 1} m & = t (s + m) \cr (t + 1) m & = t (s + m) \cr t m + m & = t s + t m \cr m & = t s \cr}$$

Suppose $s > 1$ . Note that $s < m$ , since $t > 1$ . Then 1 and s are distinct divisors of m other than m, so $s = 1 + s + (\hbox{other divisors})$ , which is a contradiction.

Thus, $s = 1$ . This implies $\sigma(m) = m + 1$ , so m is prime.

Moreover, I get $m = t \cdot s = t \cdot 1 = t = 2^{a + 1} - 1$ .

It follows that $n = 2^a (2^{a + 1} - 1)$ , where $2^{a + 1} - 1$ is prime.

On the other hand, suppose $n = 2^a (2^{a + 1} - 1)$ , where $2^{a + 1} - 1$ is a Mersenne prime. Then

$$\sigma(n) = (2^{a + 1} - 1) [(2^{a + 1} - 1) + 1] = 2^{a + 1} (2^{a + 1} - 1) = 2 \cdot 2^a (2^{a + 1} - 1) = 2 n.$$

Therefore, n is an even perfect number.

Example. What perfect number corresponds to the Mersenne prime $2^7 - 1 = 127$ ?

$$2^6(2^7 - 1) = 8128 \quad\hbox{is perfect}.\quad\halmos$$

I now know that finding even perfect numbers is equivalent to finding Mersenne primes --- primes of the form $2^n - 1$ . I showed earlier that $2^n - 1$ is prime implies that n is prime. So to look for Mersenne primes, I only need to look at $2^n - 1$ for n prime. Next, I'll derive a result which simplifies checking that $2^n - 1$ is prime. First, here's an amusing lemma.

Lemma. $(2^a - 1, 2^b - 1) = 2^{(a, b)} - 1$ .

Proof. Assume without loss of generality that $a \ge b$ . The greatest common divisor of two numbers doesn't change if I subtract the smaller from the larger, so

$$(2^a - 1, 2^b - 1) = \left((2^a - 1) - (2^b - 1), 2^b - 1\right) = (2^a - 2^b, 2^b - 1) = (2^b(2^{a-b} - 1), 2^b - 1).$$

Since $2^b - 1$ is odd, it has no factors in common with the $2^b$ in the first term. So

$$(2^b(2^{a-b} - 1), 2^b - 1) = (2^{a-b} - 1, 2^b - 1).$$

Now I see that the "$2^{(\cdot)} - 1$ " in each slot is just along for the ride: All the action is taking place in the exponents. And what is happening is that the subtraction algorithm for computing greatest common divisors is operating in the exponents! --- the original pair a, b, was replaced by $a - b$ , b.

It follows that the exponents will "converge" to $(a, b)$ , because this is what the subtraction algorithm does. And when the algorithm terminates, I'll have $(2^{(a, b)} - 1, 0) = 2^{(a, b)} - 1$ , proving the result.

Example. Compute $(2^{42} - 1, 2^{54} - 1)$ .

$(42, 54) = 6$ , so

$$(2^{42} - 1, 2^{54} - 1) = 2^6 - 1 = 63.$$

This is surely not obvious, especially when you consider that $2^{42} - 1 = 4398046511103$ and $2^{54} - 1 = 18014398509481983$ !

Theorem. Let p be an odd prime. Every factor of $2^p - 1$ has the form $2 k p + 1$ for some $k \ge 0$ .

Proof. It suffices to prove that the result holds for prime factors of $2^p - 1$ . For

$$(2 a p + 1)(2 b p + 1) = 2(2 a b p + a + b)p + 1,$$

so products of numbers of the form $2 k p + 1$ also have that form.

Suppose then that q is a prime factor of $2^p - 1$ . Fermat's theorem says $q \mid 2^{q-1} - 1$ . The preceding lemma implies that

$$(2^p - 1, 2^{q - 1} - 1) = 2^{(p, q - 1)} - 1.$$

Now $q \mid 2^p - 1$ and $q \mid 2^{q-1} - 1$ implies $q \mid 2^{(p,q-1)} - 1$ . In particular, $2^{(p,q-1)} - 1 > 1$ , since it's divisible by the prime q. This in turn implies that $(p, q-1) > 1$ . Now p is prime, so this is only possible if $(p, q -1) = p$ . In particular, $p \mid q - 1$ .

Write $q - 1 = t p$ , so $q = t p + 1$ . q is odd, so $q - 1$ is even, and $t p$ is even. Since p is odd, t must be even: $t = 2 k$ for some k. Then $q = 2 k p + 1$ , which is what I wanted to show.

Example. Use the $2 k p + 1$ criterion to determine whether $2^{17} - 1 = 131071$ is prime.

$\sqrt{131071} \approx 362$ . If $2^{17} - 1$ has a proper prime factor, it must have one less than 362, and the prime factor must have the form $2k\cdot 17 + 1 = 34k + 1$ . So I need to check the primes less than 362 to see if they divide 131071.

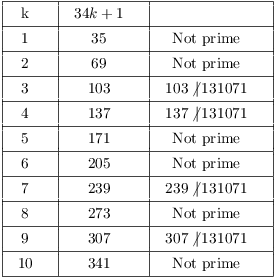
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & k & & $34k + 1$ & & & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 1 & & 35 & & Not prime & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 2 & & 69 & & Not prime & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 3 & & 103 & & $103 \notdiv 131071$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 4 & & 137 & & $137 \notdiv 131071$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 5 & & 171 & & Not prime & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 6 & & 205 & & Not prime & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 7 & & 239 & & $239 \notdiv 131071$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 8 & & 273 & & Not prime & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 9 & & 307 & & $307 \notdiv 131071$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 10 & & 341 & & Not prime & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Therefore, $2^{17} - 1$ is prime.

The $51^{\rm st}$ known Mersenne prime was discovered in 2018. It is $2^{82589933}-1$ and was found using software developed by the Great Internet Mersenne Prime Search https://www.mersenne.org.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga