Prime Power Congruences

In this section, I'll discuss how you solve polynomial congruences mod a power of a prime. The basic idea is to "lift" solutions one power at a time: Start with solutions mod p. Lift them (if possible) to solutions mod $p^2$ . Lift those (if possible) to solutions mod $p^3$ . And so on.

The general approach (where the modulus is composite) is:

1. Solve the congruence mod p, where p is prime.

2. Solve the congruence mod $p^k$ for $k \ge 2$ , where p is prime.

3. To solve the congruence mod n, let $n = p_1^{r_1} p_2^{r_2} \cdots p_k^{r_k}$ . Use step 2 to solve the congruence mod $p_i^{r_i}$ for $i = 1, \ldots k$ , then use the Chinese Remainder Theorem to put together the $p_i^{r_i}$ solutions to get a solution mod n.

First, I'll show how to use a solution to a quadratic congruence $x^2 = m \mod{p}$ for p prime to get a solution to $x^2 = m \mod{p^2}$ .

Example. Solve the quadratic congruence

$$x^2 = 12 \mod{169}.$$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & y & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $y^2 \mod{13}$ & & 0 & & 1 & & 4 & & 9 & & 3 & & 12 & & 10 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & y & & 7 & & 8 & & 9 & & 10 & & 11 & & 12 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $y^2 \mod{13}$ & & 10 & & 12 & & 3 & & 9 & & 4 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$y^2 = 12 \mod{13}$ has solutions $y = 5$ and $y = 8$ . (Note that $8 = -5 \mod{13}$ .) I will try to "lift" one of these solutions to a solution mod 169.

Write

$$x = 5 + 13 z.$$

I will try to find z so that

$$x^2 = 12 \mod{169}.$$

In other words, I suppose that a solution mod 169 is congruent mod 13 to the mod 13 solution 5.

Substitute $x = 5 + 13 z$ into $x^2 = 12 \mod{169}$ and solve:

$$\eqalign{ (5 + 13 z)^2 & = 12 \mod{169} \cr 25 + 1304 z + 169 z^2 & = 12 \mod{169} \cr 25 + 130 z & = 12 \mod{169} \cr 130 z & = -13 = 156 \mod{169} \cr}$$

I divide out the common factor of 26, dividing the modulus by $(169, 26) = 13$ :

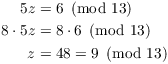
$$\eqalign{ 5 z & = 6 \mod{13} \cr 8 \cdot 5 z & = 8 \cdot 6 \mod{13} \cr z & = 48 = 9 \mod{13} \cr}$$

Note that if $z = 9 + 13 t$ , then

$$x = 5 + 13 (9 + 13 t) = 122 + 169 t.$$

Thus, any z which equals 9 mod 13 will give the same solution $x = 122 \mod{169}$ .

Note that $x = -122 = 47 \mod{169}$ is another solution. You can check that you get it by starting with the solution $y = 8$ to $y^2 = 12 \mod{13}$ .

The general theorem requires two preliminary results.

Lemma. If $k \ge 1$ , then the product of k consecutive integers is divisible by $k!$ .

Proof. First, if any of the consecutive integers is 0, the product is 0, and it is divisible by $k!$ .

Next, if all of the consecutive integers are negative, their product is equal to $(-1)^k$ times the product of k consecutive positive integers.

Hence, it suffices to prove the result for positive integers: The product of k consecutive integers is divisible by $k!$ .

Write the k consecutive positive integers in descending order as

$$n,\ n - 1,\ \ldots n - k + 1.$$

Then the product is

$$n \cdot (n - 1) \cdots (n - k + 1) = \dfrac{[n \cdot (n - 1) \cdots (n - k + 1)] (n - k) (n - k - 1) \cdots 1}{(n - k) (n - k - 1) \cdots 1} = \dfrac{n!}{(n - k)!} = k! {n \choose k}.$$

Therefore,

$$k! \mid n \cdot (n - 1) \cdots (n - k + 1).\quad\halmos$$

Proposition. Let $f(x) \in \integer[x]$ , let $n \ge 1$ , and let p be prime. For all $x, t \in \integer$ ,

$$f(x + p^n t) = f(x) + f'(x) p^n t \mod{p^{n + 1}}.$$

Proof. Let $k = \deg(f)$ . Consider the Taylor expansion of f:

$$f(x + p^n t) = f(x) + f'(x) \cdot p^n t + \dfrac{f''(x)}{2!} p^{2 n} t^2 + \dfrac{f^{(3)}(x)}{3!} p^{3 n} t^3 + \cdots + \dfrac{f^{(k)}(x)}{k!} p^{k n} t^k.$$

I need to show that

$$p^{n + 1} \mid \dfrac{f^{(j)}(x)}{j!} p^{j n} t^j \quad\hbox{for}\quad j \ge 2.$$

Since $j \ge 2$ and $n \ge 1$ ,

$$j n \ge 2 n = n + n \ge n + 1.$$

Hence, $p^{n + 1} \mid p^{j n}$ . This shows that the result is true, provided that $\dfrac{f^{(j)}(x)}{j!}$ is an integer.

Write $\displaystyle f(x) = \sum_i c_i x^i$ . Then

$$f^{(j)}(x) = \sum_i c_i (i)(i - 1) \cdots (i - j + 1) x^{i - j}.$$

Each coefficient $c_i (i)(i - 1) \cdots (i - j + 1)$ has as a factor the product of j consecutive integers, which is divisible by $j!$ . Therefore, $\dfrac{f^{(j)}(x)}{j!}$ is an integer, and the argument above is complete.

Theorem. Let $f(x) \in \integer[x]$ , let $n \ge 1$ , let p be prime, and let c be a solution to $f(x) = 0 \mod{p^n}$ .

(a) If $p \notdiv f'(c)$ , then $f(x) = 0 \mod{p^{n + 1}}$ has a unique solution congruent to c mod $p^n$ . It is given by $c + p^n t$ , where

$$t = -f'(c)^{-1} \cdot \dfrac{f(c)}{p^n} \mod{p}.$$

(b) If $p \mid f'(c)$ , then:

(i) If $p^{n + 1} \mid f(c)$ , then $f(x) = 0 \mod{p^{n + 1}}$ has p solutions congruent to c mod $p^n$ . They're given by $c + p^n t$ for $t = 0, 1, \ldots, p - 1$ .

(ii) If $p^{n + 1} \notdiv f(c)$ , then $f(x) = 0 \mod{p^{n + 1}}$ has no solutions congruent to c mod $p^n$ .

Proof. Since $f(c) = 0 \mod{p^n}$ , I have $p^n \mid f(c)$ , and $\dfrac{f(c)}{p^n}$ is an integer.

Suppose first that $p \notdiv f'(c)$ . Then $f'(c)$ is invertible mod p. Let

$$t = -f'(c)^{-1} \cdot \dfrac{f(c)}{p^n}.$$

By the previous result

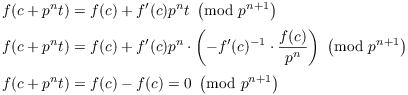
$$\eqalign{ f(c + p^n t) & = f(c) + f'(c) p^n t \mod{p^{n + 1}} \cr \noalign{\vskip2pt} f(c + p^n t) & = f(c) + f'(c) p^n \cdot \left(-f'(c)^{-1} \cdot \dfrac{f(c)}{p^n}\right) \mod{p^{n + 1}} \cr \noalign{\vskip2pt} f(c + p^n t) & = f(c) - f(c) = 0 \mod{p^{n + 1}} \cr}$$

This shows that $c + p^n t$ is a solution to $f(x) = 0 \mod{p^{n + 1}}$ , and clearly $c + p^n t = c \mod{p^n}$ .

Reversing these steps shows that t is unique mod p.

Now suppose that $p \mid f'(c)$ . Then $p^{n + 1} \mid f'(c) p^n$ , so the previous result yields

$$f(c + p^n t) = f(c) + f'(c) p^n t = f(c) + 0 = f(c) \mod{p^{n + 1}}.$$

If $p^{n + 1} \mid f(c)$ , the equation says

$$f(c + p^n t) = f(c) = 0 \mod{p^{n + 1}}.$$

Since t was arbitrary, this equation is satisfied for all of the p distinct values of t mod p, namely $t = 0, 1, \ldots p - 1$ .

Finally, if $p^{n + 1} \notdiv f(c)$ , the equation says

$$f(c + p^n t) = f(c) \ne 0 \mod{p^{n + 1}}.$$

This means that for no t is $c + p^n t$ a solution to $f(x) = 0 \mod{p^{n + 1}}$ .

Example. Solve the congruence

$$x^2 + 5 x + 18 = 0 \mod{49}.$$

Step 1. Find solutions mod 7.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 + 5 x + 18 \mod{7}$ & & 4 & & 3 & & 4 & & 0 & & 5 & & 5 & & 0 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The solutions are $x = 3$ and $x = 6$ .

Step 2. For each solution c to the congruence mod $p^n$ , determine whether p does or does not divide $f'(c)$ and consider cases.

Since $f(x) = x^2 + 5 x + 18$ , I have $f'(x) = 2 x + 5$ .

I have $f'(3) = 11$ and $7 \notdiv 11$ . I have $f'(6) = 17$ and $7 \notdiv 17$ .

I'll do $x = 3$ first. Note that $f(3) = 42$ . Applying the first case of the theorem, I solve:

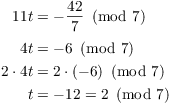
$$\eqalign{ 11 t & = -\dfrac{42}{7} \mod{7} \cr \noalign{\vskip2pt} 4 t & = -6 \mod{7} \cr 2 \cdot 4 t & = 2 \cdot (-6) \mod{7} \cr t & = -12 = 2 \mod{7} \cr}$$

Hence, a solution mod 49 is given by $3 + 7 \cdot 2 = 17$ .

Next, I'll do $x = 6$ . Note that $f(6) = 84$ . Applying the first case of the theorem, I solve:

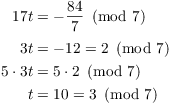
$$\eqalign{ 17 t & = -\dfrac{84}{7} \mod{7} \cr \noalign{\vskip2pt} 3 t & = -12 = 2 \mod{7} \cr 5 \cdot 3 t & = 5 \cdot 2 \mod{7} \cr t & = 10 = 3 \mod{7} \cr}$$

Hence, a solution mod 49 is given by $6 + 7 \cdot 3 = 27$ .

Example. Solve the congruence

$$x^2 + x + 7 = 0 \mod{9}.$$

First, I find solutions to $x^2 + x + 7 = 0 \mod{3}$ :

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 1 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $x^2 + x + 7 \mod{3}$ & & 1 & & 0 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

I get $x = 1 \mod{3}$ .

Take $f(x) = x^2 + x + 7$ . Then $f'(x) = 2 x + 1$ . Then $f'(1) = 3$ , and $3 \mid f'(1)$ . Therefore, we're in the second case of the theorem.

Further, $f(1) = 9$ , and $9 \mid f(1)$ . Hence, we're in the first subcase of the second case, and $x^2 + x + 7 = 0 \mod{9}$ has 3 solutions congruent to 1 mod 3. They're obtained by adding multiples of 3 to 1: We get $x = 1, 4, 7 \mod{9}$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga