Prime Numbers

Definition. An integer greater than 1 is prime if its only positive factors are 1 and itself. An integer greater than 1 which is not prime is composite.

Prime numbers are the "building blocks" of the integers. For instance, the Fundamental Theorem of Arithmetic says that every integer greater than 1 can be written uniquely as a product of powers of primes. The next lemma is a key step in the proof of the theorem, and is used in Euclid's proof that there are infinitely many primes.

Remarks. The reason 1 is not considered prime is that it makes the statement of theorems (like the Fundamental Theorem of Arithmetic) simpler.

There is a related concept in abstract algebra: A prime element in an integral domain. An element x in an integral domain R is prime if $x \ne 0$ and x is not a unit, and if $x \mid y z$ , then $x \mid y$ or $x \mid z$ . Considering $\integer$ as an integral domain, the prime elements are the prime numbers together with their negatives. We won't need these notions in this course, however.

Lemma. Every integer greater than 1 is divisible by at least one prime.

Proof. I'll prove the result by induction. To begin with, the result is true for $n = 2$ , since 2 is prime.

Take $n > 2$ , and assume the result is true for all integers greater than 1 but less than n. I want to show that the result holds for n. If n is prime, it's divisible by a prime --- namely itself! So suppose n is composite. Then n has a positive factor a other than 1 and n. Suppose $n = a b$ .

If $a > n$ , then since $b \ge 1$ , I get $n = a b > n \cdot 1 = n$ , which is a contradiction. Thus, $a \le n$ , and since $a \ne n$ , I have in fact $a < n$ . Since $a \ne 1$ , I get $1 < a < n$ .

By the induction hypothesis, a has a prime factor p. But $p \mid a$ and $a \mid n$ implies $p \mid n$ , so n has a prime factor as well. This shows that the result is true for all $n > 1$ by induction.

The following theorem and its proof occur as Proposition 20 in Book 9 of Euclid's Elements.

Theorem. (Euclid) There are infinitely many prime numbers.

Proof. Suppose on the contrary that there are only finitely many primes $p_1$ , $p_2$ , ..., $p_n$ . Look at

$$p_1\cdot p_2\cdot \cdots \cdot p_n + 1.$$

This number is not divisible by any of the primes $p_1$ , $p_2$ , ..., $p_n$ , because it leaves a remainder of 1 when divided by any of them. But the previous lemma says that every number greater than 1 is divisible by a prime. This contradiction implies that there can't be finitely many primes --- that is, there are infinitely many.

If you are trying to factor a number n, you do not need to try dividing by all the numbers from 1 to n: It's enough to go up to $\sqrt{n}$ . This is the idea of the next lemma.

Lemma. Every composite number has a proper factor less than or equal to its square root.

Proof. Suppose n is composite. I can write $n = a b$ , where $1 < a, b < n$ . If both $a, b > \sqrt{n}$ , then

$$n = \sqrt{n} \cdot \sqrt{n} < a \cdot b = n.$$

This contradiction shows that at least one of a, b must be less than or equal to $\sqrt{n}$ .

In fact, you can adapt the preceding proof to show that a composite number must have a prime factor less than or equal to its square root.

For an arbitrary number that is several hundred digits in length, it may be impossible with current technology to determine whether the number is prime. In fact, many cryptographic systems depend on the difficulty of factoring large numbers.

Example. What primes must you divide 127 by to test whether it is prime? To see whether 127 is prime, I only need to see if it has a prime factor $\le \sqrt{127} \approx 11.27$ . You can do the arithmetic to verify that 127 isn't divisible by 2, 3, 5, 7, or 11. Hence, it must be prime.

Example. ( The Sieve of Eratosthenes) The sieve is a method for generating a list of primes by hand. Write down the integer beginning with 2. Go through the list, crossing out every integer divisible by 2. Then go through the list, crossing out every integer divisible by 3. Keep going.

Illustrate the first two passes through Sieve of Eratosthenes for the numbers from 1 to 50.

I've illustrated the first two passes below.

$$\hbox{\epsfysize=2.5in \epsffile{primes1.eps}}$$

By the square root criterion above, I've already found all the primes less than 10, namely 2, 3, 5, and 7. After crossing out all the numbers divisible by 5, I'll have all the primes up to 25. And so on. Of course, more sophisticated sieve methods are used in practice.

I showed above that there are infinitely many primes. How are they distributed? That is, are they evenly distributed, or do they get "sparser" as you look at bigger and bigger integers? The Prime Number Theorem gives an aymptotic estimate for $\pi(x)$ , the number of primes less than or equal to x. It says:

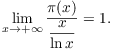
$$\lim_{x\to +\infty} \dfrac{\pi(x)}{\dfrac{x}{\ln x}} = 1.$$

Here are the graphs of $\pi(x)$ and $\dfrac{x}{\ln x}$ .

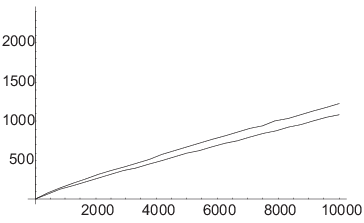
$$\hbox{\epsfysize=2in \epsffile{primes2.eps}}$$

The graph of $\pi(x)$ is on top and the graph of $\dfrac{x}{\ln x}$ is on the bottom.

The Prime Number Theorem was first conjectured by Legendre and Gauss. The first rigorous proofs were given by Hadamard and de la Vallee Poussin around 1896. Elementary proofs were given by Atle Selberg and Paul Erd\"os in the 1930's.

On the other hand, there are "lots" of composite numbers around. For example, here is a run of 1000 consecutive composite numbers:

$$1001! + 2, 1001! + 3, 1001! + 4, \ldots, 1001! + 1001.$$

You can use the same method to generate runs of composite numbers of any length.

Example. Use the Prime Number Theorem to estimate the number of primes less than $1\,000\,000$ .

By the Prime Number Theorem,

$$\pi(1\,000\,000) \approx \dfrac{1\,000\,000}{\ln 1\,000\,000} \approx 72\,382.$$

The actual number of primes less than $1\,000\,000$ is $\pi(1\,000\,000) = 78\,498$ .

On the other hand, many problems concerning the distribution of primes are unsolved. For example, there are primes that come in pairs (two units apart), such as 11 and 13, or 71 and 73. These are called twin primes.

Question: ( Twin Prime Conjecture) Are there infinitely many twin primes?

There are enormously large twin primes known. The largest pair currently known were discovered in 2011, and are

$$3756801695685 \cdot  2^{666669} \pm 1.$$

The Twin Prime Conjecture is still unresolved: A proof is announced every now and then, but no proof has passed the scrutiny of the mathematics community yet.

Example. Find all prime numbers p such that $11 p + 9$ is a perfect square.

Write

$$11 p + 9 = x^2.$$

Note that if $x = 0$ , then $11 p + 9 = 0$ , which has no solutions since the left side must be positive.

Further, I may assume $x > 0$ . For if $x < 0$ , then $-x > 0$ , and $-x$ also satisfies the equation:

$$(-x)^2 = x^2 = 11 p + 9.$$

In other words, if there are x's that work, there must be positive x's that work.

Now rewrite the equation:

$$\eqalign{ 11 p & = x^2 - 9 \cr 11 p & = (x + 3)(x - 3) \cr}$$

Since $x > 0$ , I have $x + 3 > 0$ . Now $11 p$ and $x + 3$ are positive, so $x - 3$ must be positive as well.

Thus, the equation expresses $11 p$ as a product of two positive numbers. Since 11 and p are prime, there are 4 ways to do this. I consider each of the cases.

Case 1: $x + 3 = 11$ and $x - 3 = p$ .

The first equation gives $x = 8$ , so the second equation says $p = 8 - 3 = 5$ , which is prime. This is a solution.

Case 2: $x + 3 = p$ and $x - 3 = 11$ .

The second equation gives $x = 14$ , so the first equation says $p = 14 + 3 = 17$ , which is prime. This is a solution.

Case 3: $x + 3 = 11 p$ and $x - 3 = 1$ .

The second equation gives $x = 4$ , so the first equation says $7 = 4 + 3 = 11 p$ . This is a contradiction, because $11 \notdiv 7$ .

Case 4: $x + 3 = 1$ and $x - 3 = 11 p$ .

The first equation gives $x = -2$ , but this is ruled out by the assumption that $x > 0$ .

All together, the primes p for which $11 p + 9$ is a perfect square are $p = 5$ and $p = 17$ .

A great resource for prime numbers is the Prime Pages at http://primes.utm.edu.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga