If x and y are the legs of a right triangle and z is the hypotenuse,
then Pythagoras' theorem says ![]() . A triple of integers
. A triple of integers
![]() is a Pythagorean triple if it
satisfies
is a Pythagorean triple if it
satisfies ![]() . (In what follows, I'll assume that x, y,
and z are positive integers.)
. (In what follows, I'll assume that x, y,
and z are positive integers.)
For example ![]() is a Pythagorean triple, since
is a Pythagorean triple, since ![]() .
. ![]() is also a Pythagorean triple, but
there is a sense in which it's "redundant":
is also a Pythagorean triple, but
there is a sense in which it's "redundant": ![]() . If a Pythagorean triple is not a proper
multiple of of another triple, it is said to be
primitive. Thus,
. If a Pythagorean triple is not a proper
multiple of of another triple, it is said to be
primitive. Thus, ![]() is a primitive Pythagorean triple
if
is a primitive Pythagorean triple
if ![]() .
.
The result I'll prove will show how you can generate all primitive Pythagorean triples.
Theorem.
(a) Suppose a and b are positive numbers, one is even and the other
is odd, ![]() , and
, and ![]() . Then
. Then
![]()
is a primitive Pythagorean triple.
(b) Suppose ![]() is a primitive Pythagorean triple. Then one
of x, y is even and the other is odd. If x is even, then there are
positive numbers a and b, such that one is even and the other is odd,
is a primitive Pythagorean triple. Then one
of x, y is even and the other is odd. If x is even, then there are
positive numbers a and b, such that one is even and the other is odd,
![]() ,
, ![]() , and
, and
![]()
A similar statement holds if y is even.
Proof. (a)
![]()
Therefore, ![]() is a Pythagorean triple. I have to show
it's primitive.
is a Pythagorean triple. I have to show
it's primitive.
Suppose on the contrary that ![]() , where p is prime. One
of a, b, is even and the other is odd, so y and z must be odd. On the
other hand, x is even. Therefore,
, where p is prime. One
of a, b, is even and the other is odd, so y and z must be odd. On the
other hand, x is even. Therefore, ![]() .
.
Now ![]() and
and ![]() implies
implies ![]() .
Since
.
Since ![]() ,
, ![]() . Since p is prime,
. Since p is prime, ![]() .
.
Likewise, ![]() and
and ![]() implies
implies ![]() . Since
. Since ![]() ,
, ![]() . Since p is
prime,
. Since p is
prime, ![]() .
.
This is a contradiction, because ![]() .
.
Therefore, ![]() , and
, and ![]() is a primitive
Pythagorean triple.
is a primitive
Pythagorean triple.
(b) Suppose ![]() is a primitive Pythagorean triple, so
is a primitive Pythagorean triple, so ![]() and
and ![]() . First, I'll show that one of x,
y must be even and the other odd.
. First, I'll show that one of x,
y must be even and the other odd.
If both x and y are even, then ![]() is even, so z is even.
This contradicts
is even, so z is even.
This contradicts ![]() .
.
Suppose both x and y are odd. Note that the square of an odd number is congruent to 1 mod 4:
![]()
So ![]() . This is impossible,
because only 0, 1, and 4 are squares mod 4.
. This is impossible,
because only 0, 1, and 4 are squares mod 4.
Therefore, one of x, y must be even and the other odd. Suppose x is
even and y is odd. Note that ![]() must be odd, so z must
be odd. This means that
must be odd, so z must
be odd. This means that ![]() and
and ![]() are even. Then
are even. Then
![]()
and ![]() ,
, ![]() , and
, and ![]() are all
integers.
are all
integers.
Next, I'll show that ![]() . Suppose p is a prime and
. Suppose p is a prime and ![]() . Then
. Then
![]()
![]()
![]()
This contradicts ![]() . Thus,
. Thus, ![]() .
.
Now ![]() expresses a product of two
relatively prime integers as a perfect square. By the Fundamental
Theorem of Arithmetic, each of the numbers on the right must be a
perfect square:
expresses a product of two
relatively prime integers as a perfect square. By the Fundamental
Theorem of Arithmetic, each of the numbers on the right must be a
perfect square:
![]()
Note that ![]() , for if p is prime and
, for if p is prime and ![]() , then
, then ![]() .
.
If a and b are both odd or both even, then ![]() and
and ![]() are both even, contrary to assumption. Hence, one of
a, b, is odd and the other is even.
are both even, contrary to assumption. Hence, one of
a, b, is odd and the other is even.
Finally,
![]()
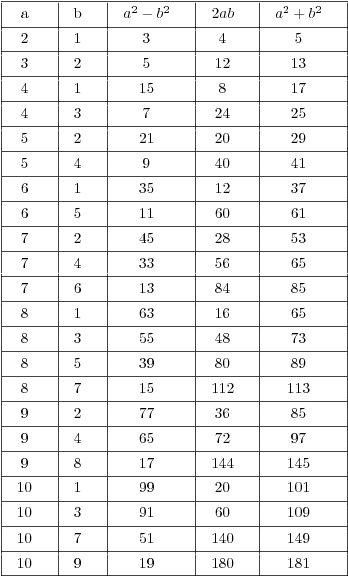
Example. Take ![]() . Choose a number b
that is less than 21, such that b has different parity than 21 (so b
is even), and such that
. Choose a number b
that is less than 21, such that b has different parity than 21 (so b
is even), and such that ![]() . For example, let
. For example, let ![]() . Then
. Then
![]()
Since
![]()
![]() is a primitive Pythagorean triple.
is a primitive Pythagorean triple.![]()
Example. You can use the theorem to generate
all primitive Pythagorean triples. To do this, fix the bigger number
a. Then consider b's less than a such that b is of different parity
than a and such that ![]() . These requirements on b
eliminate many possibilities. For each pair of numbers a and b, the
formulas in the theorem give the elements x, y, and z of the triple.
. These requirements on b
eliminate many possibilities. For each pair of numbers a and b, the
formulas in the theorem give the elements x, y, and z of the triple.
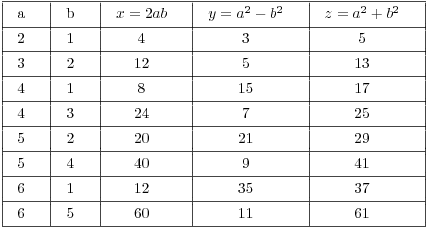
For example, consider ![]() . Then b must be less than 6,
relatively prime to 6, and odd. Thus, the only possibilities are
. Then b must be less than 6,
relatively prime to 6, and odd. Thus, the only possibilities are ![]() and
and ![]() , and these give the last two cases above.
, and these give the last two cases above.![]()
Example. Let ![]() be a Pythagorean
triple. Show that one of x, y, z is divisible by 5.
be a Pythagorean
triple. Show that one of x, y, z is divisible by 5.
Mod 5 the only squares are 0, 1, and 4.
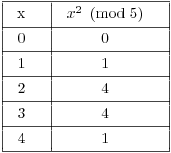
Suppose neither x nor y is divisible by 5. Then ![]() and
and ![]() can be either 1 or 4 mod 5. Consider the
possibilities for
can be either 1 or 4 mod 5. Consider the
possibilities for ![]() :
:
![]()
![]()
![]()
![]()
In the only cases which are possible, z is divisible by 5.
Thus, one of x, y, z must be divisible by 5.![]()
Copyright 2005 by Bruce Ikenaga