Quadratic Reciprocity

Theorem. ( Gauss's Lemma) Let p be an odd prime, $(a, p) = 1$ . Let k be the number of least positive residues of

$$a, 2 a, \ldots, \dfrac{p - 1}{2} a \quad\hbox{greater than}\quad \dfrac{p}{2}.$$

Then

$$\legendre a p = (-1)^k.$$

Proof. Since p is odd, $\dfrac{p}{2}$ is not an integer. Hence, every residue of a, $2 a$ , ..., $\dfrac{p - 1}{2} a$ is either less than $\dfrac{p}{2}$ or greater than $\dfrac{p}{2}$ . Label these two sets:

$$a_1, \ldots, a_j < \dfrac{p}{2}, \quad b_1, \ldots, b_k > \dfrac{p}{2}.$$

Thus, $j + k = \dfrac{p - 1}{2}$ .

Step 1 $\left\{p - b_1, \ldots, p - b_k, a_1, \ldots, a_j\right\} = \left\{1, 2, \ldots, \dfrac{p - 1}{2}\right\}$ .

The $a_i$ 's are contained in $\left\{1, 2, \ldots, \dfrac{p - 1}{2}\right\}$ , because the $a_i$ 's are less than $\dfrac{p}{2}$ (so less than or equal to $\dfrac{p - 1}{2}$ ).

What about the $p - b_i$ 's?

$$b_i > \dfrac{p}{2}, \quad\hbox{so}\quad p - b_i < p - \dfrac{p}{2} = \dfrac{p}{2}.$$

Since $p - b_i$ is an integer and $\dfrac{p}{2}$ is an integer plus one-half, I have $p - b_i \le \dfrac{p - 1}{2}$ . This shows that the $p - b_i$ 's are contained in $\left\{1, 2, \ldots, \dfrac{p - 1}{2}\right\}$ as well.

There are $\dfrac{p - 1}{2}$ elements in $\left\{1, 2, \ldots, \dfrac{p - 1}{2}\right\}$ , and $j + k = \dfrac{p - 1}{2}$ . So if the $a_i$ 's and $p - b_i$ 's are all distinct, I'll know the two sets are equal.

Each $a_i$ has the form $r a$ , where $1 \le r \le \dfrac{p - 1}{2}$ . So if $r a$ and $s a$ are the same, then

$$r a = s a \mod{p}, \quad\hbox{so}\quad p \mid (r - s)a.$$

$p \notdiv a$ , so $p \mid (r - s)$ . This is impossible for $1 \le r, s \le \dfrac{p - 1}{2}$ unless $r = s$ --- which implies $r a = s a$ to begin with.

A similar argument shows that the $b_i$ 's, and hence the $p - b_i$ 's, are distinct.

Could $a_i = p - b_h$ ? $a_ i = r a$ and $p - b_h = p - s a$ for $1 \le r, s \le \dfrac{p - 1}{2}$ , so

$$p - s a = r a \mod{p}, \quad r a + s a = 0 \mod{p}, \quad p \mid (r + s) a.$$

Again, $p \notdiv a$ , so $p \mid (r + s)$ . But $1 \le r, s \le \dfrac{p - 1}{2}$ implies $2 \le r + s \le p - 1$ , so $p \mid (r + s)$ is impossible.

This finishes the proof that $\left\{p - b_1, \ldots, p - b_k, a_1, \ldots, a_j\right\} = \left\{1, 2, \ldots, \dfrac{p - 1}{2}\right\}$ .

Step 2 Since the two sets are the same, the products of the elements in the two sets are the same:

$$(p - b_1)\cdots (p - b_k)\cdot a_1\cdots a_j = \left(\dfrac{p - 1}{2}\right)! \mod{p}.$$

Now $p - b_i = -b_i \mod{p}$ , so

$$(-1)^k b_1 \cdots b_k \cdot a_1 \cdots a_j = \left(\dfrac{p - 1}{2}\right)! \mod{p}.$$

But the a's and b's are exactly the residues of the numbers $a, 2 a, \ldots, \dfrac{p - 1}{2}a$ , so I may replace the product of the a's and b's with the product of $a, 2 a, \ldots, \dfrac{p - 1}{2}a$ :

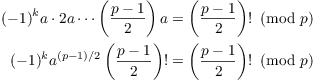
$$\eqalign{ (-1)^k a \cdot 2 a \cdots \left(\dfrac{p - 1}{2}\right) a & = \left(\dfrac{p - 1}{2}\right)! \mod{p} \cr (-1)^k a^{(p - 1)/2} \left(\dfrac{p - 1}{2}\right)! & = \left(\dfrac{p - 1}{2}\right)! \mod{p} \cr}$$

Now $\left(p,\dfrac{p - 1}{2}\right) = 1$ , so I can cancel the $\left(\dfrac{p - 1}{2}\right)!$ terms from both sides. Then applying Euler's theorem, I get

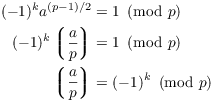
$$\eqalign{ (-1)^k a^{(p - 1)/2} & = 1 \mod{p} \cr (-1)^k \legendre a p & = 1 \mod{p} \cr \legendre a p & = (-1)^k \mod{p} \cr}$$

I made the last step by multiplying both sides by $(-1)^k$ and using the fact that $(-1)^{2 k} = 1$ .

Example. Use Gauss's Lemma to compute $\legendre{6}{7}$ .

Since $p = 7$ , I have $\dfrac{p}{2} = 3.5$ and $\dfrac{p - 1}{2} = 3$ . Look at the residues $1 \cdot 6 = 6$ , $2 \cdot 6 = 5$ , and $3 \cdot 6 = 4$ . All three are greater than 3.5 --- they're $b_i$ 's, in the notation of the proof of Gauss's Lemma --- so Gauss's Lemma says

$$\legendre{6}{7} = (-1)^3 = -1.$$

As a check, Euler's theorem gives $\legendre 6 7 = 6^3 = -1 \mod{7}$ .

The following technical lemma will be needed for the proof of reciprocity.

Lemma. Let $a, b > 0$ , where b is an odd integer. Then

$$a = b \cdot \left(\left[\dfrac{a}{b}\right] + e\right) + (-1)^e \cdot r \quad\hbox{for}\quad e = 0 \quad\hbox{or}\quad 1, \quad 0 \le r \le \dfrac{b - 1}{2}.$$

Here $\left[\cdot\vphantom{\dfrac{a}{b}}\right]$ denotes the greatest integer function and $\left[\dfrac{a}{b}\right] + e$ is the integer closest to $\dfrac{a}{b}$ .

Proof. By the Division Algorithm,

$$a = b q + r, \hbox{ where } 0 \le r < b.$$

Now $\dfrac{b}{2}$ is not an integer, so either $r < \dfrac{b}{2}$ or $r > \dfrac{b}{2}$ .

(For example, if $a = 11$ and $b = 3$ , then $r = 2 > \dfrac{3}{2} = \dfrac{b}{2}$ , while if $a = 11$ and $b = 5$ , $r = 1 < \dfrac{5}{2} = \dfrac{b}{2}$ .)

Consider the two cases.

Case 1: $r < \dfrac{b}{2}$ .

Write

$$a = b \cdot \left(\left[\dfrac{a}{b}\right] + 0\right) + (-1)^0 \cdot r.$$

Here $e = 0$ , and $\left[\dfrac{a}{b}\right] + 0$ is the integer closest to $\dfrac{a}{b}$ . $r < \dfrac{b}{2}$ , but $\dfrac{b}{2}$ is not an integer, so $r \le \dfrac{b - 1}{2}$ , and $0 \le r \le \dfrac{b - 1}{2}$ .

Case 2: $r > \dfrac{b}{2}$ .

Write

$$a = b \cdot \left(\left[\dfrac{a}{b}\right] + 1\right) + (r - b) = b \cdot \left(\left[\dfrac{a}{b}\right] + 1\right) + (-1)^1 \cdot (b - r).$$

Here $e = 1$ , and $\left[\dfrac{a}{b}\right] + 1$ is the integer closest to $\dfrac{a}{b}$ . $r < b$ , so $b - r > 0$ . Now $r > \dfrac{b}{2}$ , so $-r < -\dfrac{b}{2}$ , or $b - r < b - \dfrac{b}{2} = \dfrac{b}{2}$ . Since $\dfrac{b}{2}$ is not an integer, $b - r \le \dfrac{b - 1}{2}$ . Therefore, $0 \le r \le \dfrac{b - 1}{2}$ .

Example. Illustrate the lemma with:

(a) $a = 42$ and $b = 17$ .

(b) $a = 50$ and $b = 17$ .

(a) For $a = 42$ and $b = 17$ , I have $\dfrac{42}{17} \approx 2.47$ , so the integer closest to $\dfrac{42}{17}$ is 2. Then

$$42 = 17 \cdot 2 + 8.$$

And $0 \le 8 \le \dfrac{17 - 1}{2}$ .

(b) For $a = 50$ and $b = 17$ , I have $\dfrac{50}{17} = 2.94$ , so the integer closest to $\dfrac{50}{17}$ is 3. Then

$$50 = 17 \cdot 3 + (-1) \cdot 1.$$

And $0 \le 1 \le \dfrac{17 - 1}{2}$ .

In other words, the r in the lemma represents the distance from a to the nearest multiple of b.

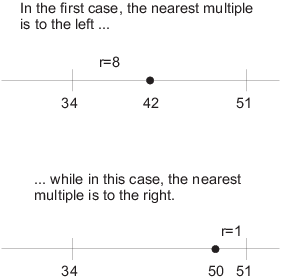
$$\hbox{\epsfysize=2.5 in \epsffile{quadratic-reciprocity1.eps}}$$

The $\pm$ is needed depending on whether the nearest multiple is less than or greater than a.

I'll use the lemma to give an ingenious proof of Quadratic Reciprocity due to J.S.~Frame [1].

Theorem. ( Quadratic Reciprocity) Let p and q be distinct odd primes.

$$\legendre p q \legendre q p = (-1)^{\left(\dfrac{p - 1}{2}\right)\left(\dfrac{q - 1}{2}\right)}$$

Proof. To simplify the writing, let $p' = \dfrac{p - 1}{2}$ and $q' = \dfrac{q - 1}{2}$ .

Let $1 \le n \le q'$ . Apply the Lemma with $a = n p$ and $b = q$ :

$$n p = q \cdot \left(\left[\dfrac{n p}{q}\right] + e_n\right) + (-1)^{e_n}r_n.$$

Here $1 \le r_n \le q'$ and $e_n = 0$ or 1.

The first thing I will show is that the remainders $r_n$ are just a permutation of the integers 1, ..., $q'$ .

If I take the initial equation and reduce mod q, I get

$$n p = (-1)^{e_n} r_n \mod{q}.$$

Can two of the r's be equal? Suppose $r_m = r_n$ , where $1 \le m, n \le q'$ . Then

$$0 = r_m - r_n = \left((-1)^{e_m} m - (-1)^{e_n} n\right)p \mod{q}.$$

In other words, $q \mid \left((-1)^{e_m} m - (-1)^{e_n} n\right)p$ . But $m + n \le 2 q' = q - 1$ , so $(-1)^{e_m} m - (-1)^{e_n} n$ is surely smaller than q in absolute value. Since $q \notdiv p$ , this is impossible unless $(-1)^{e_m} m - (-1)^{e_n} n = 0$ . This in turn is impossible unless $m = n$ . Thus, the r's are distinct. Since there are $q'$ of them, and since they're all in the range $[1, q']$ , they must be some permutation of the numbers 1, ..., $q'$ .

As a preliminary to the next computation, take the first equation and reduce mod 2. Now p and q are odd, so they equal 1 mod 2. Also, $(-1)^{e_n} = \pm 1$ , and it both cases $(-1)^{e_n} = 1 \mod{2}$ . Therefore,

$$n = \left[\dfrac{n p}{q}\right] + e_n + r_n \mod{2}.$$

(I'm going to use this in an exponent of -1 in a second!)

Now let $1 \le m \le p'$ , $1 \le n \le q'$ . Then $m q - n p \ne 0$ , for $m q = n p$ implies $p \mid m$ --- which is impossible, because $1 \le m \le p' = \dfrac{p - 1}{2}$ .

Now here's the heart of the proof. The idea will be to define a weird product which turns out to be the Legendre symbol. Define

$$f(p, q) = \prod_{m = 1}^{p'} \prod_{n = 1}^{q'} \dfrac{m q - n p}{|m q - n p|}.$$

Notice that $\dfrac{m q - n p}{|m q - n p|}$ is a fancy way of expressing the sign of $m q - n p$ --- $+1$ when it's positive, -1 when it's negative.

When is $m q - n p$ negative?

$$\eqalign{ m q - n p & < 0 \cr m q & < n p \cr \noalign{\vskip2pt} m & < \dfrac{n p}{q} \cr \noalign{\vskip2pt} m & \le \left[\dfrac{n p}{q}\right] \cr}$$

That is, $m q - n p$ is negative for $m = 1, \ldots, \left[\dfrac{n p}{q}\right]$ . So the product for $f(p, q)$ for fixed n has $\left[\dfrac{n p}{q}\right]$ terms equal to -1, and

$$f(p, q) = \prod_{n = 1}^{q'} (-1)^{[n p/q]}.$$

(The terms equal to 1 contribute nothing to the product.)

Now

$$\eqalign{ n & = \left[\dfrac{n p}{q}\right] + e_n + r_n \mod{2} \cr n - r_n - e_n & = \left[\dfrac{n p}{q}\right] \mod{2} \cr n - r_n + e_n & = \left[\dfrac{n p}{q}\right] \mod{2} \cr}$$

The last equality comes from the fact that $-e_n = e_n \mod{2}$ .

Now if $a = b \mod{2}$ then $(-1)^a = (-1)^b$ . So

$$f(p, q) = \prod_{n = 1}^{q'} (-1)^{n - r_n + e_n} = \prod_{n = 1}^{q'} (-1)^{n - r_n} (-1)^{e_n} = (-1)^{\sum_{n = 1}^{q'} (n - r_n)} \prod_{n = 1}^{q'} (-1)^{e_n}.$$

Since the $r_n$ 's are just the integers from 1 to $q'$ and since n runs from 1 to $q'$ , the sum of the $r_n$ 's is the same as the sum of the n's from 1 to $q'$ , and

$$\sum_{n = 1}^{q'} (n - r_n) = \sum_{n = 1}^{q'} n - \sum_{n = 1}^{q'} r_n = 0.$$

So the previous equation becomes

$$f(p, q) = \prod_{n = 1}^{q'} (-1)^{e_n}.$$

Recall from above that

$$n p = (-1)^{e_n} r_n \mod{q}.$$

Now $r_n$ is invertible mod q, so I may write

$$\dfrac{n p}{r_n} = (-1)^{e_n} \mod{q}.$$

Plugging this into the last equation for $f(p, q)$ , I get

$$f(p, q) = \prod_{n = 1}^{q'} \dfrac{n p}{r_n} \mod {q}.$$

But $\displaystyle \prod_{n = 1}^{q'} \dfrac{n}{r_n} = 1$ , because as n runs over the numbers from 1 to $q'$ , so does $r_n$ . So by Euler's theorem,

$$f(p, q) = \prod_{n = 1}^{q'} p = p^{q'} = \legendre{p}{q}.$$

Notice that

$$f(q, p) = \prod_{m = 1}^{q'} \prod_{n = 1}^{p'} \dfrac{m p - n q}{|m p - n q|} = \prod_{m = 1}^{p'} \prod_{n = 1}^{q'} \dfrac{n p - m q}{|n p - m q|}.$$

I got the second product by swapping m and n in the first.

Whew! The rest is easy --- fortunately!

$$\legendre{p}{q} \legendre{q}{p} = f(p, q) f(q, p) = \prod_{m=1}^{p'} \prod_{n = 1}^{q'} \dfrac{m q - n p}{|m q - n p|} \dfrac{n p - m q}{|n p - m q|} = \prod_{m=1}^{p'} \prod_{n = 1}^{q'} (-1) = (-1)^{p'q'}.$$

Since $p' = \dfrac{p - 1}{2}$ and $q' = \dfrac{q - 1}{2}$ , I'm done!

As complicated as this proof is, it's actually no worse than most proofs of this result.

Before giving an example, I want to discuss what reciprocity tells you about solutions to quadratic congruences.

An odd prime p is congruent to 1 or to 3 mod 4.

If $p = 4 k + 1$ , then $\dfrac{p - 1}{2} = 2 k$ , an even number. If $p = 4 k + 3$ , then $\dfrac{p - 1}{2} = 2 k + 1$ , an odd number.

Since an even number times anything is even,

$$\dfrac{p - 1}{2}\cdot \dfrac{q - 1}{2} = \cases{ \hbox{even} & if p or $q = 1 \mod{4}$ \cr \hbox{odd} & if p and $q = 3 \mod{4}$ \cr}$$

Therefore,

$$\legendre{p}{q} \legendre{q}{p} = (-1)^{\dfrac{p - 1}{2}\cdot\dfrac{q - 1}{2}} = \cases{ +1 & if p or $q = 1 \mod{4}$ \cr -1 & if p and $q = 3 \mod{4}$ \cr}$$

However,

$$\legendre{p}{q} \legendre{q}{p} = +1 \quad\hbox{means}\quad \legendre{p}{q} = \legendre{q}{p} = 1 \quad\hbox{or}\quad \legendre{p}{q} = \legendre{q}{p} = -1$$

$$\legendre{p}{q} \legendre{q}{p} = -1 \quad\hbox{means one of}\quad \legendre{p}{q}, \legendre{q}{p} \quad\hbox{is}\quad +1 \quad\hbox{and the other is}\quad -1$$

Consider the congruences

$$x^2 = p \mod{q} \quad\hbox{and}\quad x^2 = q \mod{p}.$$

This means:

1. If at least one of p, q is congruent to 1 mod 4, then both equations are solvable or both equations are unsolvable.

2. If both p and q are congruent to 3 mod 4, then one equation is solvable and the other is unsolvable.

Corollary. Let p and q be distinct odd primes.

(a) If at least one of p, q is congruent to 1 mod 4, then

$$\legendre{p}{q} = \legendre{q}{p}.$$

(b) If both p and q are congruent to 3 mod 4, then

$$\legendre{p}{q} = -\legendre{q}{p}.\quad\halmos$$

Example. Compute $\legendre {17}{71}$ .

$17 = 1 \mod{4}$ , so

$$\legendre{17}{71} = \legendre{71}{17} = \legendre{3}{17} = \legendre{17}{3} = \legendre{2}{3} = 2^{(3 - 1)/2} = 2 = -1 \mod{3}.$$

In other words, $x^2 = 17 \mod{71}$ does not have any solutions.

Example. Compute $\legendre{299}{359}$ .

$$\legendre{299}{359} = \legendre{13}{359} \legendre{23}{359}.$$

I'll compute $\legendre{13}{359}$ and $\legendre{23}{359}$ . First,

$$\legendre{13}{359} = \legendre{359}{13} = \legendre{8}{13} = 8^{(13 - 1)/2} = 8^6 = 262144 = -1 \mod{13}.$$

Next,

$$\legendre{23}{359} = -\legendre{359}{23} = -\legendre{14}{23} = -\legendre{2}{23} \legendre{7}{23}.$$

Next, I'll compute $\legendre{2}{23}$ and $\legendre{7}{23}$ .

$$\legendre{2}{23} = 2^{(23 - 1)/2} = 2^{11} = 2048 = 1 \mod{23}.$$

$$\legendre{7}{23} = -\legendre{23}{7} = -\legendre{2}{7} = -(2^{(7 - 1)/2}) = -8 = -1 \mod{7}.$$

Therefore, $\legendre{23}{359} = -(1)(-1) = 1$ , and

$$\legendre{299}{359} = (-1)(1) = -1.$$

In other words, the congruence $x^2 = 299 \mod{359}$ does not have a solution.

[1] J.S. Frame, A short proof of quadratic reciprocity, Amer. Math. Monthly, 85(10)(1978), 818--819.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga