The Ring of Integers

Elementary number theory is largely about the ring of integers, denoted by the symbol $\integer$ . The integers are an example of an algebraic structure called an integral domain. This means that $\integer$ satisfies the following axioms:

(a) $\integer$ has operations + (addition) and $\cdot$ (multiplication). It is closed under these operations, in that if $m, n \in \integer$ , then $m + n \in \integer$ and $m \cdot n \in \integer$ .

(b) Addition is associative: If $m, n, p \in \integer$ , then

$$m + (n + p) = (m + n) + p.$$

(c) There is an additive identity $0 \in \integer$ : For all $n \in \integer$ ,

$$n + 0 = n \quad\hbox{and}\quad 0 + n = n.$$

(d) Every element has an additive inverse: If $n \in \integer$ , there is an element $-n \in \integer$ such that

$$n + (-n) = 0 \quad\hbox{and}\quad (-n) + n = 0.$$

(e) Addition is commutative: If $m, n \in \integer$ , then

$$m + n = n + m.$$

(f) Multiplication is associative: If $m, n, p \in \integer$ , then

$$m \cdot (n \cdot p) = (m \cdot n) \cdot p.$$

(g) There is an multiplicative identity $1 \in \integer$ : For all $n \in \integer$ ,

$$n \cdot 1 = n \quad\hbox{and}\quad 1 \cdot n = n.$$

(h) Multiplication is commutative: If $m, n \in \integer$ , then

$$m \cdot n = n \cdot m.$$

(i) The Distributive Laws hold: If $m, n, p \in \integer$ , then

$$m \cdot (n + p) = m \cdot n + m \cdot p \quad\hbox{and}\quad (m + n) \cdot p = m \cdot p + n \cdot p.$$

(j) There are no zero divisors: If $m, n \in \integer$ and $m\cdot n = 0$ , then either $m = 0$ or $n = 0$ .

Remarks.

(a) As usual, I'll often abbreviate $m \cdot n$ to $m n$ .

(b) The last axiom is equivalent to the Cancellation Property: If $a, b, c \in \integer$ , $a \ne 0$ , and $a b = a c$ , then $b = c$ .

Here's the proof:

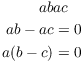
$$\eqalign{ a b & a c \cr a b - a c & = 0 \cr a (b - c) & = 0 \cr}$$

Since there are no zero divisors, either $a = 0$ or $b - c = 0$ . Since $a \ne 0$ by assumption, I must have $b - c = 0$ , so $b = c$ .

Notice that I didn't divide both sides of the equation by a --- I cancelled a from both sides. This shows that division and cancellation aren't "the same thing".

Example. If $n \in \integer$ , prove that $0 \cdot n = 0$ .

$$\matrix{ 0 \cdot n & = & (0 + 0) \cdot n & \quad\hbox{(Additive identity)} \cr & = & 0 \cdot n + 0 \cdot n & \quad\hbox{(Distributive Law)} \cr}$$

Adding $-(0 \cdot n)$ to both sides, I get

$$-(0 \cdot n) + 0 \cdot n = -(0 \cdot n) + (0 \cdot n + 0 \cdot n).$$

By associativity for addition,

$$-(0 \cdot n) + 0 \cdot n = (-(0 \cdot n) + 0 \cdot n) + 0 \cdot n.$$

Then using the fact that $-(0 \cdot n)$ and $0 \cdot n$ are additive inverses,

$$0 = 0 + 0 \cdot n.$$

Finally, 0 is the additive identity, so

$$0 = 0 \cdot n.\quad\halmos$$

Example. If $n \in \integer$ , prove that $-n = (-1) \cdot n$ .

In words, the equation says that the additive inverse of n (namely $-n$ ) is equal to $(-1) \cdot n$ . What is the additive inverse of n? It is the number which gives 0 when added to n.

Therefore, I should add $(-1) \cdot n$ and see if I get 0:

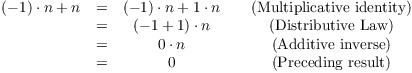
$$\matrix{(-1) \cdot n + n & = & (-1) \cdot n + 1\cdot n & \quad\hbox{(Multiplicative identity)} \cr & = & (-1 + 1) \cdot n & \quad\hbox{(Distributive Law)} \cr & = & 0 \cdot n & \quad\hbox{(Additive inverse)} \cr & = & 0 & \quad\hbox{(Preceding result)} \cr}$$

By the discussion above, this proves that $-n = (-1) \cdot n$ .

Example. Give an example of a set of objects with a "multiplication" which is not commutative.

If you have had linear algebra, you know that matrix multiplication is not commutative in general. For instance, considering $2 \times 2$ real matrices,

$$\left[\matrix{1 & 0 \cr 1 & 1 \cr}\right] \left[\matrix{1 & 1 \cr 0 & 0 \cr}\right] = \left[\matrix{1 & 1 \cr 1 & 1 \cr}\right], \quad\hbox{but}\quad \left[\matrix{1 & 1 \cr 0 & 0 \cr}\right] \left[\matrix{1 & 0 \cr 1 & 1 \cr}\right] = \left[\matrix{2 & 1 \cr 0 & 0 \cr}\right].\quad\halmos$$

The integers are ordered --- there is a notion of greater than (or less than). Specifically, for $m, n \in \integer$ , $m > n$ is defined to mean that $m - n$ is a positive integer: an element of the set $\{1, 2, 3, \ldots\}$ .

Of course, $m < n$ is defined to mean $n > m$ . $m \ge n$ and $m \le n$ have the obvious meanings.

There are several order axioms:

(k) The positive integers are closed under addition and multiplication.

(l) ( Trichotomy) If $n \in \integer$ , either $n > 0$ , $n < 0$ , or $n = 0$ .

Example. Prove that if $m > 0$ and $n < 0$ , then $m n < 0$ .

$n < 0$ , so $0 - n = -n$ is a positive integer. $m > 0$ means $m = m - 0$ is a positive integer, so by closure $m \cdot (-n)$ is a positive integer.

By a property of integers (which you should try proving from the axioms), $m \cdot (-n) = -(m n)$ . Thus, $-(m n)$ is a positive integer. So $0 - m n = -(m n)$ is a positive integer, which means that $0 > m n$ .

Well-Ordering Axiom. Every nonempty subset of the positive integers has a smallest element.

Your long experience with the integers makes this principle sound obvious. In fact, it is one of the deeper axioms for $\integer$ . Some consequences include the Division Algorithm and the principle of mathematical induction.

Example. Prove that $\root 3 \of 2$ is not a rational number.

The proof will use the Well-Ordering Property.

I'll give a proof by contradiction. Suppose that $\root 3 \of 2$ is a rational number. In that case, I can write $\root 3 \of 2 = \dfrac{a}{b}$ , where a and b are positive integers.

Now

$$\root 3 \of 2 = \dfrac{a}{b}, \quad\hbox{so}\quad b\root 3 \of 2 = a, \quad\hbox{and}\quad 2b^3 = a^3.$$

(To complete the proof, I'm going to use some divisibility properties of the integers that I haven't proven yet. They're easy to understand and pretty plausible, so this shouldn't be a problem.)

The last equation shows that 2 divides $a^3$ . This is only possible if 2 divides a, so $a = 2 c$ , for some positive integer c. Plugging this into $2 b^3 = a^3$ , I get

$$2 b^3 = 8c^3, \quad\hbox{or}\quad b^3 = 4 c^3.$$

Since 2 divides $4 c^3$ , it follows that 2 divides $b^3$ . As before, this is only possible if 2 divides b, so $b = 2 d$ for some positive integer d. Plugging this into $b^3 = 4 c^3$ , I get

$$8 d^3 = 4 c^3, \quad\hbox{or}\quad 2 d^3 = c^3.$$

This equation has the same form as the equation $2 b^3 = a^3$ , so it's clear that I can continue this procedure indefinitely to get e such that $c = 2 e$ , f such that $d = 2 f$ , and so on.

However, since $a = 2 c$ , it follows that $a > c$ ; since $c = 2 e$ , I have $c > e$ , so $a > c > e$ . Thus, the numbers a, c, e, ... comprise a set of positive integers with no smallest element, since a given number in the list is always smaller than the one before it. This contradicts Well-Ordering.

Therefore, my assumption that $\root 3 \of 2$ is a rational number is wrong, and hence $\root 3 \of 2$ is not rational.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga