Wilson's Theorem and Fermat's Theorem

Suppose p is prime. Wilson's theorem says $(p - 1)! = -1 \mod{p}$ . Fermat's theorem says if $p \notdiv a$ , then $a^{p - 1} = 1 \mod{p}$ . They are often used to reduce factorials and powers mod a prime.

I'll prove Wilson's theorem first, then use it to prove Fermat's theorem.

Lemma. Let p be a prime and let $0 < x < p$ . Then $x^2 = 1 \mod{p}$ if and only if $x = 1$ or $x = p - 1$ .

Proof. If $x = 1$ , then $x^2 = 1 \mod{p}$ . If $x = p - 1$ , then

$$x^2 = p^2 - 2 p + 1 = 1 \mod{p}.$$

Conversely, suppose $x^2 = 1 \mod{p}$ . Then

$$p \mid x^2 - 1 = (x - 1)(x + 1).$$

Since p is prime, $p \mid x - 1$ or $p \mid x + 1$ . The only number in $\{1, \ldots, p - 1\}$ which satisfies $p \mid x - 1$ is 1, and the only number in $\{1, \ldots, p - 1\}$ which satisfies $p \mid x + 1$ is $p - 1$ .

$k^2 = 1 \mod{p}$ means $k \cdot k = 1 \mod{p}$ --- that is, k is its own multiplicative inverse. So the result says that 1 and $p - 1 = -1$ are the only numbers which are their own multiplicative inverses mod p.

Theorem. (Wilson's theorem) Let $p > 1$ . p is prime if and only if

$$(p - 1)! = -1 \mod{p}.$$

Proof. Suppose p is prime. If $k \in \{1, \ldots, p - 1\}$ , then k is relatively prime to p. So there are integers a and b such that

$$a k + b p = 1, \quad\hbox{or}\quad a k = 1 \mod{p}.$$

Reducing a mod p, I may assume $a \in \{1, \ldots, p - 1\}$ .

Thus, every element of $\{1, \ldots, p - 1\}$ has a reciprocal mod p in this set. The preceding lemma shows that only 1 and $p - 1$ are their own reciprocals. Thus, the elements $2, \ldots, p - 2$ must pair up into pairs $\{x, x^{-1}\}$ . It follows that their product is 1. Hence,

$$(p - 1)! = 1 \cdot 2 \cdots (p - 2) \cdot (p - 1) = 1 \cdot 1 \cdot (p - 1) = p - 1 = -1 \mod{p}.$$

Now suppose $(p - 1)! = -1 \mod{p}$ . I want to show p is prime. Begin by rewriting the equation as $(p - 1)! + 1 = k p$ .

Suppose $p = ab$ . I may take $1 \le a, b \le p$ . If $a = p$ , the factorization is trivial, so suppose $a < p$ . Then $a \mid (p - 1)!$ (since it's one of $\{1, \ldots, p - 1\}$ ) and $a \mid p$ , so $(p - 1)! + 1 = k p$ shows $a \mid 1$ . Therefore, $a = 1$ .

This proves that the only factorization of p is the trivial one, so p is prime.

Let's see how this works in a particular case. Take $p = 11$ . Then mod 11 I have

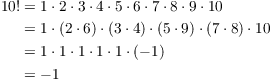
$$\eqalign{ 10! & = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 \cdot 9 \cdot 10 \cr & = 1 \cdot (2 \cdot 6) \cdot (3 \cdot 4) \cdot (5 \cdot 9) \cdot (7 \cdot 8) \cdot 10 \cr & = 1 \cdot 1 \cdot 1 \cdot 1 \cdot 1 \cdot (-1) \cr & = -1 \cr}$$

Notice how the numbers other than 1 and 10 paired up as a number and its multiplicative inverse, and how 1 and 10 are the only numbers which are their own multiplicative inverses.

Note that $(p - 1)! = -1 \mod{p}$ implies that p is prime --- but this is not a very good way to test that a number is prime. The factorials grow too rapidly.

Theorem. (Fermat) Let p be prime, and suppose $p \notdiv a$ . Then $a^{p-1} = 1 \mod{p}$ .

Proof. Consider the set of integers

$$a, 2 a, \ldots, (p - 1)a.$$

I'll show that they reduce mod p to the standard system of residues $\{1, \ldots, p - 1\}$ , then apply Wilson's theorem.

There are $p - 1$ numbers in the set $\{a, 2 a, \ldots, (p - 1)a\}$ . So all I need to do is show that they're distinct mod p. Suppose that $1 \le j, k \le p - 1$ , and

$$a j = a k \mod{p}.$$

This means $p \mid a j - a k = a(j - k)$ , so $p \mid a$ or $p \mid j - k$ . Since the first case is ruled out by assumption, $p \mid j - k$ . But since $1 \le j, k \le p - 1$ , this is only possible if $j = k$ .

Thus, $\{a, 2 a, \ldots, (p - 1)a\}$ are $p - 1$ distinct numbers mod p. So if I reduce mod p, I must get the numbers in $\{1, \ldots, p - 1\}$ . Hence,

$$a \cdot 2 a \cdots (p - 1)a = 1 \cdot 2 \cdots (p - 1) = (p - 1)! = -1 \mod{p}.$$

On the other hand, another application of Wilson's theorem shows that

$$a \cdot 2 a \cdots (p - 1)a = a^{p-1} (p - 1)! = -a^{p-1} \mod{p}.$$

So $-a^{p-1} = -1 \mod{p}$ , or $a^{p-1} = 1 \mod{p}$ .

Corollary. If p is prime, then $a^p = a \mod{p}$ for all a.

Proof. If $p \mid a$ , then $a^p = 0 \mod{p}$ and $a = 0 \mod{p}$ , so $a^p = a \mod{p}$ .

If $p \notdiv a$ , then $a^{p-1} = 1 \mod{p}$ . Multiplying by a, I get $a^p = a \mod{p}$ again.

Example. Reduce $50^{250} \mod{83}$ to a number in the range $\{0, 1, \ldots 82\}$ . (Note: 83 is prime.)

If you multiply out $50^{250}$ , here's what you get: $52714787526044456024726519219225572551424023323922008641517022$

$09078987540239533171017648022222644649987502681255357847020768$

$63325972445883937922417317167855799198150634765625000000000000$

$00000000000000000000000000000000000000000000000000000000000000$

$00000000000000000000000000000000000000000000000000000000000000$

$00000000000000000000000000000000000000000000000000000000000000$

$0000000000000000000000000000000000000000000000000000$

Now just reduce mod 83. Heh.

If you don't have access to software that can do this, you can use Fermat's theorem. First, 83 is prime and $83 \notdiv 50$ , so Fermat says $50^{82} = 1 \mod{83}$ .

Now

$$250 = 3 \cdot 82 + 4.$$

Hence,

$$50^{250} = 50^{246} \cdot 50^4 = (50^{82})^3 \cdot 6250000 = 1^3 \cdot 6250000 = 17 \mod{83}.$$

In other words, if you're trying to reduce $a^k$ mod p, where $p \notdiv a$ , factor out as many $a^{p-1}$ 's as possible, then reduce the rest "by hand".

Example. Reduce $47^{222} \mod{113}$ to a number in the range $\{0, 1, \ldots 112\}$ . (Note that 113 is prime.)

Since 113 is prime and $113 \notdiv 47$ , Fermat's theorem gives $47^{112} = 1 \mod{113}$ . So

$$47^{222} \mod{113} = 47^{112} \cdot 47^{110} = 1 \cdot 47^{110} = 47^{110} \mod{113}.$$.

Next,

$$\eqalign{ x & = 47^{110} \mod{113} \cr 47^2 \cdot x & = 47^2 \cdot 47^{110} \mod{113} \cr 2209 x & = 47^{112} \mod{113} \cr 62 x & = 1 \mod{113} \cr}$$

I need to compute $62^{-1} \mod{113}$ .

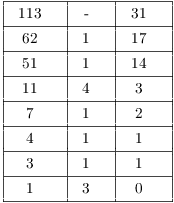
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 113 & & - & & 31 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 62 & & 1 & & 17 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 51 & & 1 & & 14 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 11 & & 4 & & 3 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 7 & & 1 & & 2 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 4 & & 1 & & 1 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 3 & & 1 & & 1 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 1 & & 3 & & 0 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\eqalign{ (-17) \cdot 113 + 31 \cdot 62 & = 1 \cr 31 \cdot 62 & = 1 \mod{113} \cr}$$

Hence, $62^{-1} = 31 \mod{113}$ . So

$$\eqalign{ 31 \cdot 62 x & = 31 \cdot 1 \mod{113} \cr x & = 31 \mod{113} \cr} \quad\halmos$$

Example. Compute

$$12 \cdot 13 \cdots 20 \cdot 21 \mod{11}.$$

The any ten consecutive numbers, none divisible by 11, reduce mod 11 to $\{1, 2, \ldots, 10\}$ . Hence,

$$12 \cdot 13 \cdots 20 \cdot 21 = 10! = -1 = 10 \mod{11}.\quad\halmos$$

Example. Simplify $\dfrac{130!}{87} \mod{131}$ to a number in the range $\{0, 1, \ldots, 130\}$ .

By Wilson's theorem, $130! = -1 \mod{131}$ . So

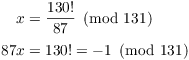
$$\eqalign{ x & = \dfrac{130!}{87} \mod{131} \cr \noalign{\vskip2 pt} 87 x & = 130! = -1 \mod{131} \cr}$$

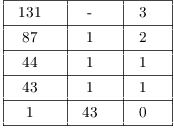
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 131 & & - & & 3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 87 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 44 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 43 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 43 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$1 = (87, 131) = (-3) \cdot 87 + 2 \cdot 131.$$

It follows that $87^{-1} = 128 \mod{131}$ , so

$$\eqalign{ 128 \cdot 87 x & = 128 \cdot (-1) \mod{131} \cr x & = -128 = 3 \mod{131} \quad\halmos \cr}$$

Example. Simplify $146! \mod{149}$ to a number in the range $\{0, 1, \ldots 148\}$ .

Note: 149 is prime.

By Wilson's theorem, $148! = -1 \mod{149}$ .

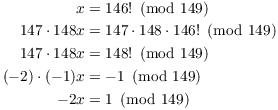
$$\eqalign{ x & = 146! \mod{149} \cr 147 \cdot 148 x & = 147 \cdot 148 \cdot 146! \mod{149} \cr 147 \cdot 148 x & = 148! \mod{149} \cr (-2) \cdot (-1) x & = -1 \mod{149} \cr -2 x & = 1 \mod{149} \cr}$$

Now $-2^{-1} = 74 \mod{149}$ , so

$$\eqalign{ 74 \cdot -2 x & = 74 \cdot 1 \mod{149} \cr x & = 74 \mod{149} \quad\halmos \cr}$$

The next problem shows how you can often deal with composite moduli: Factor the modulus into a product of (powers of) primes, solve the problem relative to the prime (power) moduli, then combine the results using the Chinese Remainder Theorem to answer the original question.

Example. Find the least nonnegative residue of $70! \mod{5183}$ .

Note: $5183 = 71 \cdot 73$ .

I'll start by finding the residues of $x = 70!$ mod 71 and 73.

By Wilson's theorem,

$$x = 70! = -1 \mod{71}.$$

Next, let $x = 70! \mod{73}$ . Then

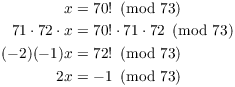
$$\eqalign{ x & = 70 ! \mod{73} \cr 71 \cdot 72 \cdot x & = 70! \cdot 71 \cdot 72 \mod{73} \cr (-2)(-1) x & = 72! \mod{73} \cr 2 x &= -1 \mod{73} \cr}$$

Note that $2 \cdot 37 = 74 = 1 \mod{73}$ . So

$$\eqalign{ 37 \cdot 2 x & = 37 \cdot(-1) \mod{73} \cr x & = -37 = 36 \mod{73} \cr}$$

Thus,

$$x = -1 \mod{71} \quad\hbox{and}\quad x = 36 \mod{73}.$$

I'll the the iterative method of the Chinese Remainder Theorem to get a congruence mod 5183. First, $x = -1 \mod{71}$ means $x = -1 + 71 a$ for some $a \in \integer$ . Plugging this into the second congruence yields

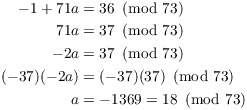
$$\eqalign{ -1 + 71 a & = 36 \mod{73} \cr 71 a & = 37 \mod{73} \cr -2 a & = 37 \mod{73} \cr (-37)(-2 a) & = (-37)(37) \mod{73} \cr a & = -1369 = 18 \mod{73} \cr}$$

The last congruence means that $a = 18 + 73 b$ for some $b \in \integer$ . Plugging this into $x = -1 + 71 a$ gives

$$x = -1 + 71(18 + 73 b) = 1277 + 5183 b, \quad\hbox{or}\quad x = 70! = 1277 \mod{5183}.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga