Review Problems for the Final

Math 161

These problems are intended to help you study for the final. However, you shouldn't assume that each problem on this handout corresponds to a problem on the final. Nor should you assume that if a topic doesn't appear here, it won't appear on the final.

1. Compute $\displaystyle \lim_{x \to 0} \dfrac{\sin 3 x - \sin 5 x}{\sin 2 x}$ .

2. Compute $\displaystyle \lim_{x \to \infty} \dfrac{4 x + \sqrt{x^2 + 1}}{3 x + 7}$ .

3. Compute $\displaystyle \lim_{h \to 0} \dfrac{(x + h)^{50} - x^{50}}{h}$ .

4. Compute $\displaystyle \lim_{x \to 4} \dfrac{x^2 - 3 x - 4}{x^2 - 16}$ .

5. Compute $\displaystyle \lim_{x \to 4^+} \sqrt{16 - x^2}$ .

6. Compute $\displaystyle \lim_{x \to 4} \dfrac{x^2 - 3 x - 4}{x^2 - 8 x + 16}$ .

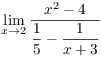7. Compute $\displaystyle \lim_{x \to 2} \dfrac{x^2 - 4}{\dfrac{1}{5} - \dfrac{1}{x + 3}}$ .

8. Compute the following limit: $\displaystyle \lim_{x \to 1} \dfrac{2 - 2 e^{x-1}}{\sin (x - 1)}$ .

9. Compute the following limit: $\displaystyle \lim_{x \to 3} \dfrac{x^3 - 2 x^2 - 2 x - 3}{2 x^3 - 6 x^2 + x - 3}$ .

10. Compute the following limit: $\displaystyle \lim_{x \to 0^+} \sqrt{x} \ln x$ .

11. Compute the following limit: $\displaystyle \lim_{x \to 0} \dfrac{\cos 2 x}{x^2 + 3 x + 1}$ .

12. Compute the following limit: $\displaystyle \lim_{x \to \infty} \left(1 + \dfrac{3}{x}\right)^{2 x}$ .

13. Compute the following limit: $\displaystyle \lim_{x \to +\infty} \left(\sqrt{x^2 + 4 x} - x\right)$ .

14. Compute the following limit: $\displaystyle \lim_{x \to 0} \dfrac{\sin 4 x + \tan 5 x}{x\cos 3 x + 12 x}$ .

15. Compute the following limit: $\displaystyle \lim_{x \to 0} \dfrac{x - x\cos x}{x\sin x + 2 x}$ .

16. Compute the following limit: $\displaystyle \lim_{x \to 0^+} \left(e^{2 x} + x\right)^{1/x}$ .

17. Compute the following limit: $\displaystyle \lim_{x \to \infty} \dfrac{x^2 + \ln x}{5 x^2 + x + 1}$ .

18. Compute the following limit: $\displaystyle \lim_{x \to \infty} \left(1 + \dfrac{5}{x^2}\right)^{3 x^2}$ .

19. Compute the following limit: $\displaystyle \lim_{x \to \infty} \left(\sqrt{x^2 + 8 x} - x\right)$ .

20. Compute the following limit: $\displaystyle \lim_{x \to \infty} \left(1 + \dfrac{2}{x}\right)^{3 x}$ .

21. Compute the derivative: $\der {} x \left(\dfrac{x}{(2 x + 1)^2}\right)$ .

22. Compute the derivative: $\der {} x \left(\ln (e^x + 1) + e^{\ln x + 1}\right)$ .

23. Compute the derivative: $\der {} x \ln\left[1 + \ln\left(1 + \ln x\right)\right]$ .

24. Compute the derivative: $\der {} x 7^{\sin x} = (\ln 7)(7^{\sin x})(\cos x)$ .

25. Compute the derivative: $\der {} x \sin \left(\dfrac{x^2 + 2}{x^2 + 3}\right)$ .

26. Compute the derivative: $\der {} x \sqrt{\dfrac{\cos x + 2}{\sin x + 4}}$ .

27. Compute the derivative: $\der {} x (x^5 + 4 x^3 - \ln x)(\sin x + 37)$ .

28. Compute the derivative: $\der {} x \sqrt{(x^3 + 5 x + 1)^7 + x}$ .

29. Compute $\der y x$ , where $x \sin y - \cos y + \cos 2 y = 0$ .

30. Compute $\der y x$ , where $y = (e^x + 2)^{x^2+3}$ .

31. Compute $y''$ when $x = 1$ and $y = 1$ , where $x^2 y^3 - x^3 = x + y - 2$ .

32. Find the points on the curve $x^4 + y^4 = 4 x y$ where $y' = 0$ .

33. Compute the following derivatives:

(a) $\displaystyle \der {} x \left((\arctan x)^5 + \arctan (x^5)\right)$ .

(b) $\displaystyle \der {} x \arcsin (e^x + 1)$ .

(c) $\displaystyle \der {} x (\tan^{-1} (\sec^{-1} x))$ .

(d) $\displaystyle \der {} x \dfrac{\cos x}{\cos^{-1} x}$ .

(e) $\displaystyle \der {} x \sqrt{\sin^{-1} x + x}$ .

(f) $\displaystyle \der {} x \tan^{-1} (e^x + 1)$ .

34. Prove that $e^x > 1 + x$ for $x \ne 0$ .

35. Graph $y = 3 x^{5/3} - \dfrac{3}{8} x^{8/3}$ .

36. Graph $y = \dfrac{(x - 5)(x + 4)}{(x - 1)^2}$ .

The derivatives are

$$y' = \dfrac{-(x - 4)}{(x - 1)^3} \quad\hbox{and}\quad y'' = \dfrac{2 (x - 6)}{(x - 1)^4}.$$

37. Compute $\displaystyle \int (e^{2 x} + e^{3 x})^2\,dx$ .

38. Compute $\displaystyle \int \dfrac{2 x + 3}{(x + 1)^4}\,dx$ .

39. Compute $\displaystyle \int \dfrac{e^{2 x}}{e^{2 x} + 1}\,dx$ .

40. Compute $\displaystyle \int \dfrac{(3\ln x)^2 + 1}{x}\,dx$ .

41. Compute $\displaystyle \int \dfrac{\cos x}{(\sin x)^2 + 2\sin x + 1}\,dx$ .

42. Compute $\displaystyle \int \dfrac{x^2 + x}{\root 3 \of {2 - 3 x^2 - 2 x^3}}\,dx$ .

43. Compute $\displaystyle \int \dfrac{\left(\sec x^{1/3}\right)^2}{x^{2/3}}\,dx$ .

44. Compute $\displaystyle \int_0^1 \dfrac{x\ln (x^2 + 1)}{x^2 + 1}\,dx$ .

45. Compute $\displaystyle \int_1^2 \dfrac{f'(x)}{f(x)}\,dx$ , if $f(1) = 1$ and $f(2) = e$ .

46. Compute $\displaystyle \int (x + 1) 4^{(x^2 + 2 x + 5)}\,dx$ .

47. Compute $\displaystyle \int \dfrac{3^x}{2^x}\,dx$ .

48. Compute $\displaystyle \int \dfrac{1}{e^x\sqrt{1 - e^{-2 x}}}\,dx$ .

49. Compute $\displaystyle \int \dfrac{1}{\sqrt{x}(1 + x)}\,dx$ .

50. Suppose $f(2) = 5$ and $f'(2) = -7$ . Assuming that f has a differentiable inverse, what is $(f^{-1})'(5)$ ?

51. Find $(f^{-1})'(5)$ for $f(x) = x^7 + 8 x - 4$ .

52. Given that $f(x) = x^5 + 4 x^3 + 17$ , what is $(f^{-1})'(22)$ ?

53. Find the largest interval containing $x = 1$ on which the function $f(x) = 3 x^4 - 16 x^3 + 1$ has an inverse $f^{-1}$ .

54. The position of a bowl of potato salad at time t is

$$s(t) = 2 t^3 - 30 t^2.$$

(a) Find the velocity $v(t)$ and the acceleration $a(t)$ .

(b) When is the velocity equal to 0? When is the acceleration equal to 0?

55. A population of flamingo lawn ornaments grows exponentially in Calvin's yard. There are 20 after 1 day and 60 after 4 days. How many are there after 6 days?

56. A bacon, sausage, onion, mushroom, and ham quiche is placed in a $400^\circ$ oven. The initial temperature of the quiche is $80^\circ$ ; after 10 minutes, the quiche's temperature is $200^\circ$ . What is the quiche's temperature 25 minutes after being placed in the oven?

57. A hot pastrami sandwich with a temperature of $150^\circ$ is placed in a $70^\circ$ room to cool. After 10 minutes, the temperature of the sandwich is $90^\circ$ . When will the temperature be $80^\circ$ ?

58. Find the area of the region in the first quadrant bounded on the left by $y = x^2$ , on the right by $x + y = 2$ , and below by the x-axis.

59. Find the area of the region between $y = 12 - x^2$ and $y = x$ from $x = 0$ to $x = 4$ .

60. Find the area of the region bounded by

$$x = y^2 - 2 y \quad\hbox{and}\quad x = 4 - y^2.$$

61. Approximate the area under $y = (x - \sin x)^2$ from $x = 3$ to $x = 5$ using 20 rectangles of equal width, and using the midpoints of each subinterval to obtain the rectangles' heights.

62. Find the exactly value of $\displaystyle \int_{-3}^0 (7 + 5 \sqrt{9 - x^2})\,dx$ .

63. Write the following sum using summation notation, then approximate its value to 5 decimal places:

$$\dfrac{3 + \sin 2}{1^2 + 1} + \dfrac{3 + \sin 3}{2^2 + 2} + \dfrac{3 + \sin 4}{3^2 + 3} + \cdots + \dfrac{3 + \sin 41}{40^2 + 40}.$$

64. Calvin runs south toward Phoebe's house at 2 feet per second. Bonzo runs east away from Phoebe's house at 5 feet per second. At what rate is the distance between Calvin and Bonzo changing when Calvin is 50 feet from the house and Bonzo is 120 feet from the house?

65. A bird flies at a constant speed of 16 feet per second at a constant height of 48 feet. Its path takes it directly over a camera, which turns to track the bird. At what rate is the acute angle between the ground and the line of sight from the camera to the bird changing 4 second after it has passed above the camera?

66. Find the dimensions of the rectangle with the largest possible perimeter that can be inscribed in a semicircle of radius 1.

67. A window is made in the shape of a rectangle with an isosceles right triangle on top.

$$\hbox{\epsfysize=1.75 in \epsffile{final-review-11.eps}}$$

(a) Write down an expression for the total area of the window.

(b) Write down an expression for the perimeter of the window (that is, the length of the outside edge).

(c) If the perimeter is given to be 4, what value of s makes the total area a maximum?

68. A cylindrical can with a top and a bottom is to be made with $96 \pi$ square inches of sheet metal with no waste. What values for the radius r and the height h give the can of largest volume?

69. A rectangular box with a square bottom and no top has a volume of 55296 cubic inches. What values of the length x of a side of the bottom and the height y give the box with the smallest total surface area (the area of the bottom plus the area of the sides)?

70. (a) Find the absolute max and the absolute min of $y = x^3 - 12 x + 5$ on the interval $0 \le x \le 5$ .

(b) Find the absolute max and the absolute min of $f(x) = \dfrac{3}{4}x^{4/3} - 15 x^{1/3}$ on the interval $-1 \le x \le 8$ .

71. Use a limit of a rectangle sum to find the exact area under $y = x^2 + 3 x$ from $x = 0$ to $x = 1$ .

72. (a) Compute $\displaystyle \der {} x \int_4^{x^6} \sqrt{2 + t^2}\,dt$ .

(b) Compute $\displaystyle \int \left(\der {} x {\root 3 \of {x^2 + 1}}\right)\,dx$ .

73. Use the definition of the derivative as a limit to prove that $\der {} x \dfrac{1}{x - 4} = -\dfrac{1}{(x - 4)^2}$ .

74. Compute $\displaystyle \lim_{h\to 0} \dfrac{1}{h} \int_x^{x+h} \sqrt{t^4 + 1}\,dt$ .

Hint: Write the limit as a difference quotient that gives the derivative of a certain function.

75. Let

$$f(x) = \cases{\dfrac{x + 3}{6 - x} & if $x < 1$ \cr \noalign{\vskip2 pt} 0.9 & if $x = 1$ \cr 3 x^2 - 2.2 & if $x > 1$ \cr}.$$ Is f continuous at $x = 1$? Why or why not?

76. Suppose that $f(3) = 5$ and $f'(x) = \dfrac{x^2}{x^2 + 16}$ . Use differentials to approximate $f(2.99)$ to 5 places.

77. A differentiable function satisfies $\der y x = e^x \cos 3 x$ and $y(0) = 0.1$ . Use differentials to approximate $y(0.02)$ .

78. Use 3 iterations of Newton's method starting at $x = 2$ to approximate a solution to $4 - x^2 = e^x$ .

79. Suppose that f is a differentiable function, $f(8) = 3$ , and

$$f'(x) > 7 \quad\hbox{for all}\quad x.$$

Prove that $f(10) > 17$ .

80. Prove that the function $f(x) = x^3 + 2 x - \cos x + 5$ has exactly one root.

\centerline{\bigssbold Solutions to the Review Problems for the Final}

1. Compute $\displaystyle \lim_{x \to 0} \dfrac{\sin 3 x - \sin 5 x}{\sin 2 x}$ .

$$\lim_{x \to 0} \dfrac{\sin 3 x - \sin 5 x}{\sin 2 x} = \lim_{x \to 0} \dfrac{\dfrac{\sin 3 x}{x} - \dfrac{\sin 5 x}{x}} {\dfrac{\sin 2 x}{x}} = \lim_{x \to 0} \dfrac{3\cdot\dfrac{\sin 3 x}{3 x} - 5\cdot\dfrac{\sin 5 x}{5 x}}{2\cdot\dfrac{\sin 2 x}{2 x}} = \dfrac{3 - 5}{2} = -1.\quad\halmos$$

2. Compute $\displaystyle \lim_{x \to \infty} \dfrac{4 x + \sqrt{x^2 + 1}}{3 x + 7}$ .

$$\lim_{x \to \infty} \dfrac{4 x + \sqrt{x^2 + 1}}{3 x + 7} = \lim_{x \to \infty} \dfrac{4 + \sqrt{1 + \dfrac{1}{x^2}}} {3 + \dfrac{7}{x}} = \dfrac{4 + 1}{3 + 0} = \dfrac{5}{3}.\quad\halmos$$

3. Compute $\displaystyle \lim_{h \to 0} \dfrac{(x + h)^{50} - x^{50}}{h}$ .

The limit represents the derivative of $f(x) = x^{50}$ :

$$\lim_{h \to 0} \dfrac{(x + h)^{50} - x^{50}}{h} = f'(x),$$

Hence, by the Power Rule,

$$\lim_{h \to 0} \dfrac{(x + h)^{50} - x^{50}}{h} = 50 x^{49}.\quad\halmos$$

4. Compute $\displaystyle \lim_{x \to 4} \dfrac{x^2 - 3 x - 4}{x^2 - 16}$ .

$$\lim_{x \to 4} \dfrac{x^2 - 3 x - 4}{x^2 - 16} = \lim_{x \to 4} \dfrac{(x + 1)(x - 4)}{(x - 4)(x + 4)} = \lim_{x \to 4} \dfrac{x + 1}{x + 4} = \dfrac{5}{8}.\quad\halmos$$

5. Compute $\displaystyle \lim_{x \to 4^+} \sqrt{16 - x^2}$ .

$x \to 4^+$ means that we're approaching 4 from the right --- that is, through numbers larger than 4.

For x close to 4 but larger than 4 --- e.g. $x = 4.01$ --- $16 - x^2$ is negative. Since the square root of a negative number is undefined, the limit is undefined.

6. Compute $\displaystyle \lim_{x \to 4} \dfrac{x^2 - 3 x - 4}{x^2 - 8 x + 16}$ .

$$\lim_{x \to 4} \dfrac{x^2 - 3 x - 4}{x^2 - 8 x + 16} = \lim_{x \to 4} \dfrac{(x - 4)(x + 1)}{(x - 4)^2} = \lim_{x \to 4} \dfrac{x + 1}{x - 4}.$$

Plugging in gives $\dfrac{5}{0}$ . Moreover,

$$\lim_{x \to 4^+} \dfrac{x + 1}{x - 4} = +\infty \quad\hbox{and}\quad \lim_{x \to 4^-} \dfrac{x + 1}{x - 4} = -\infty.$$

Hence, the limit is undefined.

7. Compute $\displaystyle \lim_{x \to 2} \dfrac{x^2 - 4}{\dfrac{1}{5} - \dfrac{1}{x + 3}}$ .

$$\lim_{x \to 2} \dfrac{x^2 - 4}{\dfrac{1}{5} - \dfrac{1}{x + 3}} = \lim_{x \to 2} \dfrac{x^2 - 4}{\dfrac{x + 3}{5(x + 3)} - \dfrac{5}{5(x + 3)}} = \lim_{x \to 2} \dfrac{x^2 - 4}{\dfrac{x + 3 - 5}{5(x + 3)}} = \lim_{x \to 2} \dfrac{x^2 - 4}{\dfrac{x - 2}{5(x + 3)}} = \lim_{x \to 2} \dfrac{(x - 2)(x + 2)}{\dfrac{x - 2}{5(x + 3)}} =$$

$$\lim_{x \to 2} (x - 2)(x + 2)\cdot \dfrac{5(x + 3)}{x - 2} = \lim_{x \to 2} 5(x + 3)(x + 2) = 100.\quad\halmos$$

8. Compute the following limit: $\displaystyle \lim_{x \to 1} \dfrac{2 - 2 e^{x-1}}{\sin (x - 1)}$ .

$$\lim_{x \to 1} \dfrac{2 - 2 e^{x-1}}{\sin (x - 1)} = \lim_{x \to 1} \dfrac{-2 e^{x-1}}{\cos (x - 1)} = \dfrac{-2}{1} = -2.\quad\halmos$$

9. Compute the following limit: $\displaystyle \lim_{x \to 3} \dfrac{x^3 - 2 x^2 - 2 x - 3}{2 x^3 - 6 x^2 + x - 3}$ .

$$\lim_{x \to 3} \dfrac{x^3 - 2 x^2 - 2 x - 3}{2 x^3 - 6 x^2 + x - 3} = \lim_{x \to 3} \dfrac{3 x^2 - 4 x - 2}{6 x^2 - 12 x + 1} = \dfrac{27 - 12 - 2}{54 - 36 + 1} = \dfrac{13}{19}.\quad\halmos$$

10. Compute the following limit: $\displaystyle \lim_{x \to 0^+} \sqrt{x} \ln x$ .

$$\lim_{x \to 0^+} \sqrt{x} \ln x = \lim_{x \to 0^+} \dfrac{\ln x}{\dfrac{1}{\sqrt{x}}} = \lim_{x \to 0^+} \dfrac{\dfrac{1}{x}}{-\dfrac{1}{2 x^{3/2}}} = \lim_{x \to 0^+} -2 x^{1/2} = 0.\quad\halmos$$

11. Compute the following limit: $\displaystyle \lim_{x \to 0} \dfrac{\cos 2 x}{x^2 + 3 x + 1}$ .

$$\lim_{x \to 0} \dfrac{\cos 2 x}{x^2 + 3 x + 1} = 1.$$

L'H\^opital's rule doesn't apply, because plugging in $x = 0$ gives 1, which is not an indeterminate form.

12. Compute the following limit: $\displaystyle \lim_{x \to \infty} \left(1 + \dfrac{3}{x}\right)^{2 x}$ .

Set $y = \left(1 + \dfrac{3}{x}\right)^{2 x}$ , so

$$\ln y = \ln \left(1 + \dfrac{3}{x}\right)^{2 x} = 2 x \ln \left(1 + \dfrac{3}{x}\right).$$

Then

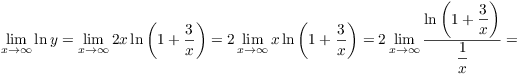
$$\lim_{x \to \infty} \ln y = \lim_{x \to \infty} 2 x \ln \left(1 + \dfrac{3}{x}\right) = 2 \lim_{x \to \infty} x \ln \left(1 + \dfrac{3}{x}\right) = 2 \lim_{x \to \infty} \dfrac{\ln \left(1 + \dfrac{3}{x}\right)}{\dfrac{1}{x}} =$$

$$2 \lim_{x \to \infty} \dfrac{\left(\dfrac{1}{1 + \dfrac{3}{x}}\right) \left(-\dfrac{3}{x^2}\right)}{\left(-\dfrac{1}{x^2}\right)} = 6.$$

So

$$\lim_{x \to \infty} \left(1 + \dfrac{3}{x}\right)^{2 x} = e^6.\quad\halmos$$

13. Compute the following limit: $\displaystyle \lim_{x \to +\infty} \left(\sqrt{x^2 + 4 x} - x\right)$ .

$$\lim_{x \to +\infty} \left(\sqrt{x^2 + 4 x} - x\right) = \lim_{x \to +\infty} \left(\sqrt{x^2 + 4 x} - x\right)\cdot \dfrac{\sqrt{x^2 + 4 x} + x}{\sqrt{x^2 + 4 x} + x} = \lim_{x \to +\infty} \dfrac{x^2 + 4 x - x^2}{\sqrt{x^2 + 4 x} + x} =$$

$$\lim_{x \to +\infty} \dfrac{4 x}{\sqrt{x^2 + 4 x} + x} = \lim_{x \to +\infty} \dfrac{4 x}{\sqrt{x^2 + 4 x} + x} \cdot \dfrac{\dfrac{1}{x}}{\dfrac{1}{x}} = \lim_{x \to +\infty} \dfrac{4}{\dfrac{1}{x}\sqrt{x^2 + 4 x} + 1} =$$

$$\lim_{x \to +\infty} \dfrac{4}{\sqrt{\dfrac{x^2 + 4 x}{x^2}} + 1} = \lim_{x \to +\infty} \dfrac{4}{\sqrt{1 + \dfrac{4}{x}} + 1} = \dfrac{4}{2} = 2.\quad\halmos$$

14. Compute the following limit: $\displaystyle \lim_{x \to 0} \dfrac{\sin 4 x + \tan 5 x}{x\cos 3 x + 12 x}$ .

$$\lim_{x \to 0} \dfrac{\sin 4 x + \tan 5 x}{x\cos 3 x + 12 x} = \lim_{x \to 0} \dfrac{4\cos 4 x + 5(\sec 5 x)^2} {-3 x\sin 3 x + \cos 3 x + 12} = \dfrac{9}{13}.\quad\halmos$$

15. Compute the following limit: $\displaystyle \lim_{x \to 0} \dfrac{x - x\cos x}{x\sin x + 2 x}$ .

$$\lim_{x \to 0} \dfrac{x - x\cos x}{x\sin x + 2 x} = \lim_{x \to 0} \dfrac{1 + x\sin x - \cos x}{x\cos x + \sin x + 2} = \dfrac{1 + 0 - 1}{0 + 0 + 2} = 0.\quad\halmos$$

16. Compute the following limit: $\displaystyle \lim_{x \to 0^+} \left(e^{2 x} + x\right)^{1/x}$ .

Set $y = \left(e^{2 x} + x\right)^{1/x}$ . Then

$$\ln y = \ln \left(e^{2 x} + x\right)^{1/x} = \dfrac{1}{x} \ln \left(e^{2 x} + x\right) = \dfrac{\ln \left(e^{2 x} + x\right)}{x}.$$

Therefore,

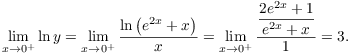
$$\lim_{x \to 0^+} \ln y = \lim_{x \to 0^+} \dfrac{\ln \left(e^{2 x} + x\right)}{x} = \lim_{x \to 0^+} \dfrac{\dfrac{2 e^{2 x} + 1}{e^{2 x} + x}}{1} = 3.$$

Hence,

$$\lim_{x \to 0^+} \left(e^{2 x} + x\right)^{1/x} = e^3.\quad\halmos$$

17. Compute the following limit: $\displaystyle \lim_{x \to \infty} \dfrac{x^2 + \ln x}{5 x^2 + x + 1}$ .

This is an indeterminate form of type $\dfrac{\infty}{\infty}$ , so I can apply L'H\^opital's rule:

$$\lim_{x \to \infty} \dfrac{x^2 + \ln x}{5 x^2 + x + 1} = \lim_{x \to \infty} \dfrac{2 x + \dfrac{1}{x}}{10 x + 1} = \lim_{x \to \infty} \dfrac{2 - \dfrac{1}{x^2}}{10} = \dfrac{2}{10} = \dfrac{1}{5}.\quad\halmos$$

18. Compute the following limit: $\displaystyle \lim_{x \to \infty} \left(1 + \dfrac{5}{x^2}\right)^{3 x^2}$ .

Let $y = \left(1 + \dfrac{5}{x^2}\right)^{3 x^2}$ . Then

$$\ln y = \ln \left(1 + \dfrac{5}{x^2}\right)^{3 x^2} = 3 x^2 \ln \left(1 + \dfrac{5}{x^2}\right).$$

Hence,

$$\lim_{x \to \infty} \ln y = \lim_{x \to \infty} 3 x^2 \ln \left(1 + \dfrac{5}{x^2}\right) = 3 \lim_{x \to \infty} \dfrac{\ln \left(1 + \dfrac{5}{x^2}\right)} {\dfrac{1}{x^2}} = 3 \lim_{x \to \infty} \dfrac{\left(\dfrac{1}{1 + \dfrac{5}{x^2}}\right) \left(-\dfrac{10}{x^3}\right)}{-\dfrac{2}{x^3}} = 15.$$

Therefore,

$$\lim_{x \to \infty} \left(1 + \dfrac{5}{x^2}\right)^{3 x^2} = e^{15}.\quad\halmos$$

19. Compute the following limit: $\displaystyle \lim_{x \to \infty} \left(\sqrt{x^2 + 8 x} - x\right)$ .

$$\lim_{x \to \infty} \left(\sqrt{x^2 + 8 x} - x\right) = \lim_{x \to \infty} \left(\sqrt{x^2 + 8 x} - x\right)\cdot \dfrac{\sqrt{x^2 + 8 x} + x}{\sqrt{x^2 + 8 x} + x} = \lim_{x \to \infty} \dfrac{x^2 + 8 x - x^2}{\sqrt{x^2 + 8 x} + x} =$$

$$\lim_{x \to \infty} \dfrac{8 x}{\sqrt{x^2 + 8 x} + x} = \lim_{x \to \infty} \dfrac{8 x}{\sqrt{x^2 + 8 x} + x} \cdot \dfrac{\dfrac{1}{x}}{\dfrac{1}{x}} = \lim_{x \to \infty} \dfrac{8}{\sqrt{1 + \dfrac{8}{x}} + 1} = \dfrac{8}{1 + 1} = 4.\quad\halmos$$

20. Compute the following limit: $\displaystyle \lim_{x \to \infty} \left(1 + \dfrac{2}{x}\right)^{3 x}$ .

Let $y = \left(1 + \dfrac{2}{x}\right)^{3 x}$ , so

$$\ln y = \ln \left(1 + \dfrac{2}{x}\right)^{3 x} = 3 x \ln \left(1 + \dfrac{2}{x}\right).$$

Then

$$\lim_{x \to \infty} \ln y = \lim_{x \to \infty} 3 x \ln \left(1 + \dfrac{2}{x}\right) = \lim_{x \to \infty} \dfrac{\ln \left(1 + \dfrac{2}{x}\right)} {\dfrac{1}{3 x}} = \lim_{x \to \infty} \dfrac{\left(\dfrac{1}{1 + \dfrac{2}{x}}\right) \left(-\dfrac{2}{x^2}\right)}{-\dfrac{1}{3 x^2}} = 6 \lim_{x \to \infty} \dfrac{1}{1 + \dfrac{2}{x}} = 6.$$

Therefore,

$$\lim_{x \to \infty} \left(1 + \dfrac{2}{x}\right)^{3 x} = \lim_{x \to \infty} y = e^{(\lim_{x \to \infty} \ln y)} = e^6.\quad\halmos$$

21. Compute the derivative: $\der {} x \left(\dfrac{x}{(2 x + 1)^2}\right)$ .

$$\der {} x \left(\dfrac{x}{(2 x + 1)^2}\right) = \dfrac{(2 x + 1)^2(1) - (x)(2)(2 x + 1)(2)}{(2 x + 1)^4}.\quad\halmos$$

22. Compute the derivative: $\der {} x \left(\ln (e^x + 1) + e^{\ln x + 1}\right)$ .

$$\der {} x \left(\ln (e^x + 1) + e^{\ln x + 1}\right) = \dfrac{e^x}{e^x + 1} + \left(\dfrac{1}{x}\right) \left(e^{\ln x + 1}\right).\quad\halmos$$

23. Compute the derivative: $\der {} x \ln\left[1 + \ln\left(1 + \ln x\right)\right]$ .

$$\der {} x \ln \left[1 + \ln \left(1 + \ln x\right)\right] = \left(\dfrac{1}{1 + \ln \left(1 + \ln x\right)}\right) \left(\dfrac{1}{1 + \ln x}\right) \left(\dfrac{1}{x}\right).\quad\halmos$$

24. Compute the derivative: $\der {} x 7^{\sin x} = (\ln 7)(7^{\sin x})(\cos x)$ .

$$\der {} x 7^{\sin x} = (\ln 7)(7^{\sin x})(\cos x).\quad\halmos$$

25. Compute the derivative: $\der {} x \sin \left(\dfrac{x^2 + 2}{x^2 + 3}\right)$ .

$$\der {} x \sin \left(\dfrac{x^2 + 2}{x^2 + 3}\right) = \left(\cos \left(\dfrac{x^2 + 2}{x^2 + 3}\right)\right) \left(\dfrac{(x^2 + 3)(2 x) - (x^2 + 2)(2 x)}{(x^2 + 3)^2}\right).\quad\halmos$$

26. Compute the derivative: $\der {} x \sqrt{\dfrac{\cos x + 2}{\sin x + 4}}$ .

$$\der {} x \sqrt{\dfrac{\cos x + 2}{\sin x + 4}} = \dfrac{1}{2}\left(\dfrac{\cos x + 2}{\sin x + 4}\right)^{-1/2} \left(\dfrac{(\sin x + 4)(-\sin x) - (\cos x + 2)(\cos x)} {(\sin x + 4)^2}\right).\quad\halmos$$

27. Compute the derivative: $\der {} x (x^5 + 4 x^3 - \ln x)(\sin x + 37)$ .

$$\der {} x (x^5 + 4 x^3 - \ln x)(\sin x + 37) = (x^5 + 4 x^3 - \ln x)(\cos x) + (\sin x + 37)\left(5 x^4 + 12 x^2 - \dfrac{1}{x}\right).\quad\halmos$$

28. Compute the derivative: $\der {} x \sqrt{(x^3 + 5 x + 1)^7 + x}$ .

$$\der {} x \sqrt{(x^3 + 5 x + 1)^7 + x} = \dfrac{1}{2}\left((x^3 + 5 x + 1)^7 + x\right)^{-1/2} \left(7(x^3 + 5 x + 1)^6 (3 x^2 + 5) + 1\right).\quad\halmos$$

29. Compute $\der y x$ , where $x \sin y - \cos y + \cos 2 y = 0$ .

Differentiate implicitly, then solve for $y'$ :

$$\eqalign{ \sin y + x y' \cos y + y' \sin y - 2 y' \sin 2 y & = 0 \cr x y' \cos y + y' \sin y - 2 y' \sin 2 y & = -\sin y \cr y' (x \cos y + \sin y - 2 \sin 2 y) & = -\sin y \cr \noalign{\vskip2 pt} y' & = \dfrac{-\sin y}{x \cos y + \sin y - 2 \sin 2 y} \cr} \quad\halmos$$

30. Compute $\der y x$ , where $y = (e^x + 2)^{x^2+3}$ .

Use logarithmic differentiation:

$$\eqalign{ \ln y & = \ln (e^x + 2)^{x^2+3} = (x^2 + 3) \ln (e^x + 2) \cr \noalign{\vskip2pt} \dfrac{y'}{y} & = 2 x \ln (e^x + 2) + \dfrac{e^x(x^2 + 3)}{e^x + 2} \cr \noalign{\vskip2pt} y' & = (e^x + 2)^{x^2+3}\left(2 x \ln (e^x + 2) + \dfrac{e^x(x^2 + 3)}{e^x + 2}\right) \cr} \quad\halmos$$

31. Compute $y''$ when $x = 1$ and $y = 1$ , where $x^2 y^3 - x^3 = x + y - 2$ .

Differentiate implicitly:

$$3 x^2 y^2 y' + 2 x y^3 - 3 x^2 = 1 + y'. \eqno{(*)}$$

Plug in $x = 1$ and $y = 1$ :

$$3 y' + 2 - 3 = 1 + y', \quad 2 y' = 2, \quad y' = 1.$$

Now differentiate (*) implicitly:

$$3 x^2 y^2 y'' + 6 x^2 y (y')^2 + 6 x y^2 y' + 6 x y^2 y' + 2 y^3 - 6 x = y''.$$

Note that the term $3 x^2 y^2 y'$ produces three terms when the Product Rule is applied.

Now set $x = 1$ , $y = 1$ , and $y' = 1$ :

$$\eqalign{ 3 y'' + 6 + 6 + 6 + 2 - 6 & = y'' \cr 2 y'' + 14 & = 0 \cr y'' & = -7 \cr} \quad\halmos$$

32. Find the points on the curve $x^4 + y^4 = 4 x y$ where $y' = 0$ .

Differentiate implicitly:

$$4 x^3 + 4 y^3 y' = 4(x y' + y).$$

Set $y' = 0$ :

$$\eqalign{ 4 x^3 + 0 & = 4(0 + y) \cr x^3 & = y \cr}$$

Substitute $y = x^3$ into $x^4 + y^4 = 4 xy$ and solve for x:

$$\eqalign{ x^4 + (x^3)^4 & = 4 x \cdot x^3 \cr x^4 + x^{12} & = 4 x^4 \cr x^{12} - 3 x^4 & = 0 \cr x^4(x^8 - 3) & = 0 \cr}$$

$x^4 = 0$ gives $x = 0$ , so $y = 0^3 = 0$ . The point is $(0, 0)$ .

$x^8 - 3 = 0$ gives $x^8 = 3$ , or $x = \pm 3^{1/8}$ . First, $x = 3^{1/8}$ gives $y = (3^{1/8})^3 = 3^{3/8}$ . Second, $x = -3^{1/8}$ gives $y = (-3^{1/8})^3 = -3^{3/8}$ . The points are $(3^{1/8}, 3^{3/8})$ and $(-3^{1/8}, -3^{3/8})$ .

The points are $(0, 0)$ , $(3^{1/8}, 3^{3/8})$ , and $(-3^{1/8}, -3^{3/8})$ .

33. Compute the following derivatives:

(a) $\displaystyle \der {} x \left((\arctan x)^5 + \arctan (x^5)\right)$ .

(b) $\displaystyle \der {} x \arcsin (e^x + 1)$ .

(c) $\displaystyle \der {} x (\tan^{-1} (\sec^{-1} x))$ .

(d) $\displaystyle \der {} x \dfrac{\cos x}{\cos^{-1} x}$ .

(e) $\displaystyle \der {} x \sqrt{\sin^{-1} x + x}$ .

(f) $\displaystyle \der {} x \tan^{-1} (e^x + 1)$ .

(a)

$$\der {} x \left((\arctan x)^5 + \arctan (x^5)\right) = 5(\arctan x)^4\cdot \dfrac{1}{x^2 + 1} + \dfrac{5 x^4}{1 + x^{10}}.\quad\halmos$$

(b)

$$\der {} x \arcsin (e^x + 1) = \dfrac{e^x}{\sqrt{1 - (e^x + 1)^2}}.\quad\halmos$$

(c)

$$\der {} x (\tan^{-1} (\sec^{-1} x)) = \left(\dfrac{1}{1 + (\sec^{-1} x)^2}\right)\left(\dfrac{1}{|x|\sqrt{x^2 - 1}}\right).\quad\halmos$$

(d)

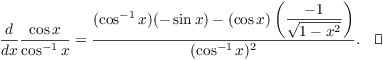
$$\der {} x \dfrac{\cos x}{\cos^{-1} x} = \dfrac{(\cos^{-1} x)(-\sin x) - (\cos x)\left(\dfrac{-1}{\sqrt{1 - x^2}}\right)}{(\cos^{-1} x)^2}.\quad\halmos$$

(e)

$$\der {} x \sqrt{\sin^{-1} x + x} = \dfrac{1}{2}\left(\sin^{-1} x + x\right)^{-1/2} \left(\dfrac{1}{\sqrt{1 - x^2}} + 1\right).\quad\halmos$$

(f)

$$\der {} x \tan^{-1} (e^x + 1) = \dfrac{e^x}{1 + (e^x + 1)^2}.\quad\halmos$$

34. Prove that $e^x > 1 + x$ for $x \ne 0$ .

$$\hbox{\epsfysize=1.5 in \epsffile{final-review-2.eps}}$$

The picture shows that the result seems to be true. However, a picture is not a proof.

Let $f(x) = e^x - (1 + x)$ . f measures the distance between the two curves. The derivative is $f'(x) = e^x - 1$ . $f' = 0$ at $x = 0$ ; since $f''(x) = e^x$ and $f''(0) = 1 > 0$ , the critical point is a local min. Since it is the only critical point, it is an absolute min.

Thus, the minimum vertical distance between the curves occurs at $x = 0$ , when it is $f(0) = 0$ . Since this is an absolute min, it follows that $f(x) > 0$ for $x \ne 0$ --- that is, $e^x - (1 + x) > 0$ for $x \ne 0$ .

Hence, $e^x > 1 + x$ for $x \ne 0$ .

35. Graph $y = 3 x^{5/3} - \dfrac{3}{8} x^{8/3}$ .

The function is defined for all x (you can take the cube root of any number).

Since $y = 3 x^{5/3}\left(1 - \dfrac{1}{8}x\right)$ , the x-intercepts are $x = 0$ and $x = 8$ . The y-intercept is $y = 0$ .

The derivatives are

$$y' = 5 x^{2/3} - x^{5/3} = x^{2/3}(5 - x), \quad y'' = \dfrac{10}{3}x^{-1/3} - \dfrac{5}{3} x^{2/3} = \dfrac{5}{3} \cdot \dfrac{2 - x}{x^{1/3}}.$$

(In working with these kinds of expressions, it is better to have a sum of terms when you're differentiating. On the other hand, it is better to have everything together in factored form when you set up the sign charts. Notice how I used these two forms in the derivatives above.)

$y' = 0$ for $x = 0$ and at $x = 5$ . $y'$ is defined for all x.

$$\hbox{\epsfxsize=2.5in \epsffile{final-review-4i.eps}}$$

The function increases for $x \le 5$ and decreases for $x \ge 5$ . There is a local max at $x = 5$ , $y \approx 16.44760$ .

$y'' = 0$ at $x = 2$ . $y''$ is undefined at $x = 0$ .

$$\hbox{\epsfxsize=2.5in \epsffile{final-review-4c.eps}}$$

The graph is concave down for $x < 0$ and for $x > 2$ . The graph is concave up for $0 < x < 2$ . $x = 0$ and $x = 2$ are inflection points.

Since the function is defined for all x, there are no vertical asymptotes.

$$\lim_{x \to +\infty} \left(3 x^{5/3} - \dfrac{3}{8} x^{8/3}\right) = -\infty \quad\hbox{and}\quad \lim_{x \to -\infty} \left(3 x^{5/3} - \dfrac{3}{8} x^{8/3}\right) = -\infty.$$

The graph goes downward on the far left and far right. There are no horizontal asymptotes.

$$\hbox{\epsfysize=2in \epsffile{final-review-4g.eps}}$$

36. Graph $y = \dfrac{(x - 5)(x + 4)}{(x - 1)^2}$ .

The derivatives are

$$y' = \dfrac{-(x - 41)}{(x - 1)^3} \quad\hbox{and}\quad y'' = \dfrac{2 (x - 61)}{(x - 1)^4}.$$

The domain is $x \ne 1$ .

The x-intercepts are $x = 5$ and $x = -4$ .

The y-intercept is $y = -20$ .

The derivatives were given:

$$y' = \dfrac{-(x - 41)}{(x - 1)^3} \quad\hbox{and}\quad y'' = \dfrac{2 (x - 61)}{(x - 1)^4}.$$

$y' = 0$ for $x = 41$ and $y'$ is undefined for $x = 1$ . Since y is undefined for $x = 1$ , this cannot be a max or a min.

$$\hbox{\epsfxsize=2.5in \epsffile{final-review-4i.eps}}$$

The function increases for $1 < x \le 41$ . It decreases for $x < 1$ and for $x \ge 41$ .

$x = 41$ is a local max.

$y'' = 0$ for $x = 61$ and $y''$ is undefined for $x = 1$ . Since y is undefined for $x = 1$ , this cannot be an inflection point.

$$\hbox{\epsfxsize=2.5in \epsffile{final-review-4c.eps}}$$

The function is concave up for $x > 61$ . It is concave down for $x < 1$ and for $1 < x < 61$ .

$x = 61$ is an inflection point.

By considering highest powers of x on the top and bottom,

$$\lim_{x \to \infty} \dfrac{(x - 5)(x + 4)}{(x - 1)^2} = 1 \quad\hbox{and}\quad \lim_{x \to -\infty} \dfrac{(x - 5)(x + 4)}{(x - 1)^2} = 1.$$

Hence, $y = 1$ is a horizontal asymptote at $\infty$ and $-\infty$ .

$$\lim_{x \to 1^+} \dfrac{(x - 5)(x + 4)}{(x - 1)^2} = -\infty \quad\hbox{and}\quad \lim_{x \to 1^-} \dfrac{(x - 5)(x + 4)}{(x - 1)^2} = -\infty.$$

$$\hbox{\epsfysize=1.75in \epsffile{final-review-1g.eps}}\quad\halmos$$

37. Compute $\displaystyle \int (e^{2 x} + e^{3 x})^2\,dx$ .

$$\int (e^{2 x} + e^{3 x})^2\,dx = \int \left(e^{4 x} + 2 e^{5 x} + e^{6 x}\right)\,dx = \dfrac{1}{4} e^{4 x} + \dfrac{2}{5}e^{5 x} + \dfrac{1}{6} e^{6 x} + C.\quad\halmos$$

38. Compute $\displaystyle \int \dfrac{2 x + 3}{(x + 1)^4}\,dx$ .

$$\int \dfrac{2 x + 3}{(x + 1)^4}\,dx = \int \dfrac{2(u - 1) + 3}{u^4}\,du = \int \dfrac{2 u + 1}{u^4}\,du = \int \left(\dfrac{2}{u^3} + \dfrac{1}{u^4}\right)\,du =$$

$$\left[u = x + 1, \quad du = dx, \quad x = u - 1\right]$$

$$-\dfrac{1}{u^2} - \dfrac{1}{3 u^3} + C = -\dfrac{1}{(x + 1)^2} - \dfrac{1}{3(x + 1)^3} + C.\quad\halmos$$

39. Compute $\displaystyle \int \dfrac{e^{2 x}}{e^{2 x} + 1}\,dx$ .

$$\int \dfrac{e^{2 x}}{e^{2 x} + 1}\,dx = \int \dfrac{e^{2 x}}{u} \cdot \dfrac{du}{2 e^{2 x}} = \dfrac{1}{2} \int \dfrac{du}{u} = \dfrac{1}{2}\ln |u| + C = \dfrac{1}{2} \ln |e^{2 x} + 1| + C.$$

$$\left[u = e^{2 x} + 1, \quad du = 2 e^{2 x}\,dx, \quad dx = \dfrac{du}{2 e^{2 x}}\right]\quad\halmos$$

40. Compute $\displaystyle \int \dfrac{(3\ln x)^2 + 1}{x}\,dx$ .

$$\int \dfrac{(3\ln x)^2 + 1}{x}\,dx = \int \dfrac{3 u^2 + 1}{x} \cdot x\,du = \int (3 u^2 + 1)\,du = u^3 + u + C = (\ln x)^3 + \ln x + C.\quad\halmos$$

$$\left[u = \ln x, \quad du = \dfrac{dx}{x}, \quad dx = x\,du\right]$$

41. Compute $\displaystyle \int \dfrac{\cos x}{(\sin x)^2 + 2\sin x + 1}\,dx$ .

$$\int \dfrac{\cos x}{(\sin x)^2 + 2\sin x + 1}\,dx = \int \dfrac{\cos x}{u^2 + 2 u + 1} \cdot \dfrac{du}{\cos x} = \int \dfrac{du}{u^2 + 2 u + 1} =$$

$$\left[u = \sin x, \quad du = \cos x\,dx, \quad dx = \dfrac{du}{\cos x}\right]$$

$$\int \dfrac{du}{(u + 1)^2} = -\dfrac{1}{u + 1} + C = -\dfrac{1}{\sin x + 1} + C.\quad\halmos$$

42. Compute $\displaystyle \int \dfrac{x^2 + x}{\root 3 \of {2 - 3 x^2 - 2 x^3}}\,dx$ .

$$\int \dfrac{x^2 + x}{\root 3 \of {2 - 3 x^2 - 2 x^3}}\,dx = \int \dfrac{x^2 + x}{\root 3 \of u} \cdot \dfrac{du}{-6(x^2 + x)} = -\dfrac{1}{6} \int u^{-1/3}\,du =$$

$$\left[u = 2 - 3 x^2 - 2 x^3, \quad du = (-6 x - 6 x^2)\,dx, \quad dx = \dfrac{du}{-6(x^2 + x)}\right]$$

$$-\dfrac{1}{6} \cdot \dfrac{3}{2}u^{2/3} + C = -\dfrac{1}{4}(2 - 3 x^2 - 2 x^3)^{2/3} + C.\quad\halmos$$

43. Compute $\displaystyle \int \dfrac{\left(\sec x^{1/3}\right)^2}{x^{2/3}}\,dx$ .

$$\int \dfrac{\left(\sec x^{1/3}\right)^2}{x^{2/3}}\,dx = \int \dfrac{\left(\sec u\right)^2}{x^{2/3}} \cdot 3 x^{2/3}\,du = 3 \int (\sec u)^2\,du = 3 \tan u + C = 3 \tan x^{1/3} + C.$$

$$\left[u = x^{1/3}, \quad du = \dfrac{1}{3}x^{-2/3}\,dx, \quad dx = 3 x^{2/3}\,du\right]\quad\halmos$$

44. Compute $\displaystyle \int_0^1 \dfrac{x\ln (x^2 + 1)}{x^2 + 1}\,dx$ .

$$\int_0^1 \dfrac{x\ln (x^2 + 1)}{x^2 + 1}\,dx = \int_1^2 \dfrac{x\ln u}{u} \cdot \dfrac{du}{2 x} =$$

$$\left[u = x^2 + 1, \quad du = 2 x\,dx, \quad dx = \dfrac{du}{2 x}; \quad x = 0, u = 1; \quad x = 1, u = 2\right]$$

$$\dfrac{1}{2} \int_1^2 \dfrac{\ln u}{u}\,du = \dfrac{1}{2} \int_0^{\ln 2} \dfrac{w}{u} \cdot u\,dw = \dfrac{1}{2} \int_0^{\ln 2} w\,dw = \dfrac{1}{2} \left[\dfrac{1}{2}w^2\right]_0^{\ln 2} = \dfrac{1}{4} (\ln 2)^2 = 0.12011 \ldots.$$

$$\left[w = \ln u, \quad dw = \dfrac{du}{u}, \quad du = u\,dw; \quad u = 1, w = 0; \quad u = 2, w = \ln 2\right]\quad\halmos$$

45. Compute $\displaystyle \int_1^2 \dfrac{f'(x)}{f(x)}\,dx$ , if $f(1) = 1$ and $f(2) = e$ .

$$\int_1^2 \dfrac{f'(x)}{f(x)}\,dx = \int_1^e \dfrac{f'(x)}{u} \cdot \dfrac{du}{f'(x)} = \int_1^e \dfrac{du}{u} = [\ln |u|]_1^e = 1.$$

$$\left[u = f(x), \quad du = f'(x)\,dx, \quad dx = \dfrac{du}{f'(x)}; \quad x = 1, u = f(1) = 1; \quad x = 2, u = f(2) = e\right] \quad\halmos$$

46. Compute $\displaystyle \int (x + 1) 4^{(x^2 + 2 x + 5)}\,dx$ .

$$\int (x + 1) 4^{(x^2 + 2 x + 5)}\,dx = \int (x + 1) 4^u \cdot \dfrac{du}{2(x + 1)} = \dfrac{1}{2} \int 4^u\,du = \dfrac{1}{2} \cdot \dfrac{1}{\ln 4}4^u + C = \dfrac{1}{2\ln 4} 4^{(x^2 + 2 x + 5)} + C.$$

$$\left[u = x^2 + 2 x + 5, \quad du = (2 x + 2)\,dx = 2(x + 1)\,dx, \quad dx = \dfrac{du}{2(x + 1)}\right]\quad\halmos$$

47. Compute $\displaystyle \int \dfrac{3^x}{2^x}\,dx$ .

I'll use the formula

$$\int a^x\,dx = \dfrac{1}{\ln a} a^x + c \quad\hbox{for}\quad a > 0.$$

In our problem,

$$\int \dfrac{3^x}{2^x}\,dx = \int \left(\dfrac{3}{2}\right)^x\,dx = \int 1.5^x\,dx = \dfrac{1}{\ln 1.5} 1.5^x + c.\quad\halmos$$

48. Compute $\displaystyle \int \dfrac{1}{e^x\sqrt{1 - e^{-2 x}}}\,dx$ .

$$\int \dfrac{1}{e^x\sqrt{1 - e^{-2 x}}}\,dx = \int \dfrac{1}{e^x\sqrt{1 - u^2}} \cdot (-e^x\,du) = -\int \dfrac{1}{\sqrt{1 - u^2}}\,du = -\sin^{-1} u + C = -\sin^{-1} e^{-x} + C.$$

$$\left[u = e^{-x}, \quad du = -e^{-x}\,dx, \quad dx = -e^x\,du\right] \quad\halmos$$

49. Compute $\displaystyle \int \dfrac{1}{\sqrt{x}(1 + x)}\,dx$ .

$$\int \dfrac{1}{\sqrt{x}(1 + x)}\,dx = \int \dfrac{1}{\sqrt{x}(1 + u^2)} \cdot 2\sqrt{x}\,du = 2 \int \dfrac{1}{1 + u^2}\,du = 2 \tan^{-1} u + C = 2 \tan^{-1} \sqrt{x} + C.$$

$$\left[u = \sqrt{x}, \quad du = \dfrac{1}{2\sqrt{x}}\,dx, \quad dx = 2\sqrt{x}\,du\right]\quad\halmos$$

50. Suppose $f(2) = 5$ and $f'(2) = -7$ . Assuming that f has a differentiable inverse, what is $(f^{-1})'(5)$ ?

$$(f^{-1})'(5) = \dfrac{1}{f'(f^{-1}(5))} = \dfrac{1}{f'(2)} = -\dfrac{1}{7}.\quad\halmos$$

51. Find $(f^{-1})'(5)$ for $f(x) = x^7 + 8 x - 4$ .

First, note that $f'(x) = 7 x^6 + 8$ .

Also, $f(1) = 1 + 8 - 4 = 5$ , so $f^{-1}(5) = 1$ .

Hence,

$$(f^{-1})'(5) = \dfrac{1}{f'(f^{-1}(5))} = \dfrac{1}{f'(1)} = \dfrac{1}{7 + 8} = \dfrac{1}{15}.\quad\halmos$$

52. Given that $f(x) = x^5 + 4 x^3 + 17$ , what is $(f^{-1})'(22)$ ?

First, $f'(x) = 5 x^4 + 12 x^2$ . Then

$$(f^{-1})'(22) = \dfrac{1}{f'(f^{-1}(22))}.$$

I need to find $f^{-1}(22)$ . Suppose $f^{-1}(22) = x$ . Then $f(x) = 22$ , so

$$x^5 + 4 x^3 + 17 = 22, \quad\hbox{and}\quad x^5 + 4 x^3 - 5 = 0.$$

I can't solve this equation algebraically. This is a case where you need to remember that this is a problem in a math course. The equation must have a solution, and probably an "easy" one --- you would not expect a solution to be something like "$x = 0.93819348 \ldots$ ".

So one approach you could take is to assume that there's an easy solution, and use trial-and-error: Try $x = 0$ , $x = 1$ , $x = -1$ , and so on. Doing so, you find that $x = 1$ works. Check: $1^5 + 4\cdot 1^3 - 5 = 0$ .

Another way to find a solution is by drawing the graph (of $y = x^5 + 4 x^3 - 5$ ):

$$\hbox{\epsfysize=1.75in \epsffile{final-review-7.eps}}$$

It looks like $x = 1$ is a solution.

Thus, $f(1) = 22$ , so $f^{-1}(22) = 1$ . Hence,

$$(f^{-1})'(22) = \dfrac{1}{f'(f^{-1}(22))} = \dfrac{1}{f'(1)} = \dfrac{1}{17}.\quad\halmos$$

53. Find the largest interval containing $x = 1$ on which the function $f(x) = 3 x^4 - 16 x^3 + 1$ has an inverse $f^{-1}$ .

The derivative is

$$f'(x) = 12 x^3 - 48 x^2 = 12 x^2(x - 4).$$

$f'(x) = 0$ for $x = 0$ and $x = 4$ . $f'(x)$ is defined for all x. Here is the sign chart for $y'$ :

$$\hbox{\epsfxsize=3 in \epsffile{final-review-9.eps}}$$

f decreases for $x \le 4$ , and this is the largest interval containing $x = 1$ on which f is always increasing or always decreasing. Therefore, the largest interval containing $x = 1$ on which the function $f(x) = 3 x^4 - 16 x^3 + 1$ has an inverse is $x \le 4$ .

54. The position of a bowl of potato salad at time t is

$$s(t) = 2 t^3 - 30 t^2.$$

(a) Find the velocity $v(t)$ and the acceleration $a(t)$ .

(b) When is the velocity equal to 0? When is the acceleration equal to 0?

(a)

$$v(t) = s'(t) = 6 t^2 - 60 t = 6 t(t - 10), \quad a(t) = v'(t) = 12 t - 60 = 12(t - 5).\quad\halmos$$

(b) The velocity is 0 at $t = 0$ and at $t = 10$ . The acceleration is 0 at $t = 5$ . at $t = 5$ .

55. A population of flamingo lawn ornaments grows exponentially in Calvin's yard. There are 20 after 1 day and 60 after 4 days. How many are there after 6 days?

Let F be the number of flamingos after t days. Then

$$F = F_0 e^{k t}.$$

When $t = 1$ , $F = 20$ :

$$20 = F_0 e^k.$$

When $t = 4$ , $F = 60$ :

$$60 = F_0 e^{4 k}.$$

Divide $60 = F_0 e^{4 k}$ by $20 = F_0 e^k$ and solve for k:

$$\eqalign{ \dfrac{60}{20} & = \dfrac{F_0 e^{4 k}}{F_0 e^k} \cr \noalign{\vskip2pt} 3 & = e^{3 k} \cr \noalign{\vskip2pt} \ln 3 & = \ln e^{3 k} = 3 k \cr \noalign{\vskip2pt} k & = \dfrac{\ln 3}{3} \cr}$$

Plug this back into $20 = F_0 e^k$ :

$$20 = F_0 e^{(\ln 3)/3} \quad\hbox{so}\quad F_0 = \dfrac{20}{e^{(\ln 3)/3}}.$$

Hence,

$$F = \dfrac{20}{e^{(\ln 3)/3}} e^{(t \ln 3)/3}.$$

When $t = 6$ ,

$$F = \dfrac{20}{e^{(\ln 3)/3}} e^{2\ln 3} = 124.805029 \ldots\ \hbox{flamingos}\quad\halmos$$

56. A bacon, sausage, onion, mushroom, and ham quiche is placed in a $400^\circ$ oven. The initial temperature of the quiche is $80^\circ$ ; after 10 minutes, the quiche's temperature is $200^\circ$ . What is the quiche's temperature 25 minutes after being placed in the oven?

The temperature of the oven is $T_e = 400$ and the initial temperature is $T_0 = 80$ . So

$$T = 400 + (80 - 400) e^{k t} = 400 - 320 e^{k t}.$$

When $t = 10$ , the temperature is $T = 200$ :

$$\eqalign{ 200 & = 400 - 320 e^{10 k} \cr -200 & = -320 e^{10 k} \cr \noalign{\vskip2 pt} \dfrac{5}{8} & = e^{10 k} \cr \noalign{\vskip2 pt} \ln \dfrac{5}{8} & = 10 k \cr \noalign{\vskip2 pt} \dfrac{1}{10} \ln \dfrac{5}{8} & = k \cr}$$

Thus,

$$T = 400 - 320 \exp \left(t \cdot \dfrac{1}{10} \ln \dfrac{5}{8}\right).$$

Remember that "$\exp({\rm FOO})$ " is another way of writing "$e^{{\rm FOO}}$ ". Also, notice that I wrote the "t" to the left of the value for k, because I don't mean t to multiply the "$\dfrac{5}{8}$ ".

Set $t = 25$ :

$$T = 400 - 320 \exp \left(25 \cdot \dfrac{1}{10} \ln \dfrac{5}{8}\right) = 301.17882 \ldots.\quad\halmos$$

57. A hot pastrami sandwich with a temperature of $150^\circ$ is placed in a $70^\circ$ room to cool. After 10 minutes, the temperature of the sandwich is $90^\circ$ . When will the temperature be $80^\circ$ ?

Let T be the temperature at time t. The initial temperature is $T_0 = 150$ , and the room's temperature is 70, so

$$T = 70 + (150 - 70)e^{kt} \quad\hbox{or}\quad T = 70 + 80 e^{kt}.$$

When $t = 10$ , $T = 90$ :

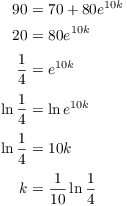
$$\eqalign{ 90 & = 70 + 80 e^{10 k} \cr 20 & = 80 e^{10 k} \cr \noalign{\vskip2pt} \dfrac{1}{4} & = e^{10 k} \cr \noalign{\vskip2pt} \ln \dfrac{1}{4} & = \ln e^{10 k} \cr \noalign{\vskip2pt} \ln \dfrac{1}{4} & = 10 k \cr \noalign{\vskip2pt} k & = \dfrac{1}{10} \ln \dfrac{1}{4} \cr}$$

Hence,

$$T = 70 + 80 e^{t (1/10) \ln (1/4)}.$$

Set $T = 80$ and solve for t:

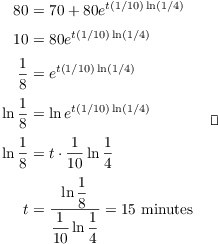
$$\eqalign{ 80 & = 70 + 80 e^{t (1/10) \ln (1/4)} \cr \noalign{\vskip2pt} 10 & = 80 e^{t (1/10) \ln (1/4)} \cr \noalign{\vskip2pt} \dfrac{1}{8} & = e^{t (1/10) \ln (1/4)} \cr \noalign{\vskip2pt} \ln \dfrac{1}{8} & = \ln e^{t (1/10) \ln (1/4)} \cr \noalign{\vskip2pt} \ln \dfrac{1}{8} & = t \cdot \dfrac{1}{10} \ln \dfrac{1}{4} \cr \noalign{\vskip2pt} t & = \dfrac{\ln \dfrac{1}{8}}{\dfrac{1}{10}\ln \dfrac{1}{4}} = 15\ \hbox{minutes} \cr} \quad\halmos$$

58. Find the area of the region in the first quadrant bounded on the left by $y = x^2$ , on the right by $x + y = 2$ , and below by the x-axis.

$$\hbox{\epsfysize=1.75in \epsffile{final-review-6.eps}}$$

The curves intersect at the point $x = 1$ , $y = 1$ . (You can see this by solving $y = x^2$ and $x + y = 2$ simultaneously.)

Divide the region up into horizontal rectangles. A typical rectangle has width $dy$ . The right end of a rectangle is on $x = 2 - y$ ; the left end of a rectangle is on $x = \sqrt{y}$ (i.e. $y = x^2$ ). Therefore, the length of a rectangle is $2 - y - \sqrt{y}$ , and the area of a rectangle is $(2 - y - \sqrt{y})\,dy$ .

The area is

$$A = \int_0^1 (2 - y - \sqrt{y})\,dy = \left[2 y - \dfrac{1}{2}y^2 - \dfrac{2}{3} y^{3/2}\right]_0^1 = \dfrac{5}{6} = 0.83333 \ldots.\quad\halmos$$

59. Find the area of the region between $y = 12 - x^2$ and $y = x$ from $x = 0$ to $x = 4$ .

$$\hbox{\epsfysize=1.75in \epsffile{final-review-8.eps}}$$

Find the intersection point:

$$\eqalign{ 12 - x^2 & = x \cr x^2 + x - 12 & = 0 \cr (x + 4)(x - 3) & = 0 \cr x = -4 & \quad\hbox{or}\quad x = 3 \cr}$$

$x = 3$ is the intersection point between 0 and 4.

Use vertical rectangles. Between $x = 0$ and $x = 3$ , the top curve is $y = 12 - x^2$ and the bottom curve is $y = x$ . Between $x = 3$ and $x = 4$ , the top curve is $y = x$ and the bottom curve is $y = 12 - x^2$ . The area is

$$\int_0^3 (12 - x^2 - x)\,dx + \int_3^4 (x - (12 - x^2))\,dx = \left[12 x - \dfrac{1}{3}x^3 - \dfrac{1}{2}x^2\right]_0^3 + \left[\dfrac{1}{2}x^2 - 12 x + \dfrac{1}{3}x^3\right]_3^4 =$$

$$\dfrac{79}{3} = 26.33333 \ldots.\quad\halmos$$

60. Find the area of the region bounded by

$$x = y^2 - 2 y \quad\hbox{and}\quad x = 4 - y^2.$$

$$\hbox{\epsfysize=1.5 in \epsffile{final-review-14.eps}}$$

Find the intersection points:

$$\eqalign{ y^2 - 2 y & = 4 - y^2 \cr 2 y^2 - 2 y - 4 & = 0 \cr y^2 - y - 2 & = 0 \cr (y - 2)(y + 1) & = 0 \cr}$$

The curves intersect at $y = -1$ and at $y = 2$ . The left-hand curve is $x = y^2 - 2 y$ and the right-hand curve is $x = 4 - y^2$ . Using horizontal rectangles, the area is

$$\int_{-1}^2 [(4 - y^2) - (y^2 - 2 y)]\,dy = \int_{-1}^2 (4 + 2 y - 2 y^2)\,dy = \left[4 y + y^2 - \dfrac{2}{3} y^3\right]_{-1}^2 = 9.\quad\halmos$$

61. Approximate the area under $y = (x - \sin x)^2$ from $x = 3$ to $x = 5$ using 20 rectangles of equal width, and using the midpoints of each subinterval to obtain the rectangles' heights.

The width of each rectangle is $\Delta x = \dfrac{5 - 3}{20} = 0.1$ .

$$\hbox{\epsfxsize=3in \epsffile{final-review-5.eps}}$$

The midpoints start at 3.05 and go to 4.95 in steps of size 0.1.

The calculator command to compute the sum is:

sum(seq((x - sin(x))$\wedge$ 2, x, 3.05, 4.95, 0.1)) * 0.1

The answer is $44.71066 \ldots$ .

62. Find the exactly value of $\displaystyle \int_{-3}^0 (7 + 5 \sqrt{9 - x^2})\,dx$ .

Note that $\displaystyle \int_{-3}^0 \sqrt{9 - x^2})\,dx$ is the area of a quarter of a circle of radius 3. So

$$\int_{-3}^0 (7 + 5 \sqrt{9 - x^2})\,dx = \int_{-3}^0 7\,dx + 5 \int_{-3}^0 \sqrt{9 - x^2})\,dx = 7 \cdot 3 + 5 \cdot \dfrac{1}{4} \pi\, 3^2 = 21 + \dfrac{45}{4} \pi.\quad\halmos$$

63. Write the following sum using summation notation, then approximate its value to 5 decimal places:

$$\dfrac{3 + \sin 2}{1^2 + 1} + \dfrac{3 + \sin 3}{2^2 + 2} + \dfrac{3 + \sin 4}{3^2 + 3} + \cdots + \dfrac{3 + \sin 41}{40^2 + 40}.$$

$$\dfrac{3 + \sin 2}{1^2 + 1} + \dfrac{3 + \sin 3}{2^2 + 2} + \dfrac{3 + \sin 4}{3^2 + 3} + \cdots + \dfrac{3 + \sin 41}{40^2 + 40} = \sum_{n=1}^{40} \dfrac{3 + \sin (n + 1)}{n^2 + n}.$$

The calculator command to do the sum is:

sum(seq((3 + sin(x + 1))/(x$\wedge$ 2 + x), x, 1, 40))

The answer is $3.31192 \ldots$ .

64. Calvin runs south toward Phoebe's house at 2 feet per second. Bonzo runs east away from Phoebe's house at 5 feet per second. At what rate is the distance between Calvin and Bonzo changing when Calvin is 50 feet from the house and Bonzo is 120 feet from the house?

Let x be the distance from Bonzo to the house, let y be the distance from Calvin to the house, and let s be the distance between Calvin and Bonzo.

$$\hbox{\epsfysize=1.75 in \epsffile{final-review-10.eps}}$$

By Pythagoras,

$$s^2 = x^2 + y^2.$$

Differentiate with respect to t:

$$2 s \der s t = 2 x \der x t + 2 y \der y t, \quad s \der s t = x \der x t + y \der y t.$$

$\der x t = 5$ and $\der y t = -2$ (negative, because his distance from the house is decreasing). When $x = 120$ and $y = 50$ , $s = 130$ . So

$$130 \der s t = (120)(5) + (50)(-2), \quad \der s t = \dfrac{50}{13} = 3.84615 \ldots\ \hbox{feet per second}.\quad\halmos$$

65. A bird flies at a constant speed of 16 feet per second at a constant height of 48 feet. Its path takes it directly over a camera, which turns to track the bird. At what rate is the acute angle between the ground and the line of sight from the camera to the bird changing 4 second after it has passed above the camera?

Let $\theta$ be the acute angle between the ground and the line of sight from the camera to the bird, and let x be the distance the bird has flown past the point directly above the camera.

$$\hbox{\epsfysize=1.5 in \epsffile{final-review-12a.eps}}$$

Then

$$\eqalign{ \tan \theta & = \dfrac{48}{x} \cr \noalign{\vskip2 pt} (\sec \theta)^2 \der \theta t & = -\dfrac{48}{x^2} \der x t \cr}$$

At 16 feet per second, the bird will have flown $x = 4 \cdot 16 = 64$ feet in 4 seconds. By Pythagoras, the hypotenuse of the triangle is $\sqrt{48^2 + 64^2} = 80$ . Hence, $\sec \theta = \dfrac{80}{64}$ .

$$\hbox{\epsfysize=1.5 in \epsffile{final-review-12b.eps}}$$

Thus,

$$\eqalign{ \left(\dfrac{80}{64}\right)^2 \der \theta t & = \left(-\dfrac{48}{64^2}\right)(16) \cr \noalign{\vskip2 pt} \der \theta y & = -\dfrac{3}{25} \quad\halmos \cr}$$

66. Find the dimensions of the rectangle with the largest possible perimeter that can be inscribed in a semicircle of radius 1.

$$\hbox{\epsfysize=2 in \epsffile{final-review-3.eps}}$$

The height of the rectangle is y; the width is $2 x$ .

The perimeter of the rectangle is

$$p = 4 x + 2 y.$$

By Pythagoras, $x^2 + y^2 = 1$ , so $y = \sqrt{1 - x^2}$ . Therefore,

$$p = 4 x + 2 \sqrt{1 - x^2}.$$

$x = 1$ gives a "flat" rectangle lying along the diameter of the semicircle. $x = 0$ gives a "thin" rectangle lying along the vertical radius.

$\der p x = 4 - \dfrac{2 x}{\sqrt{1 - x^2}}$ , so $\der p x = 0$ for $x = \dfrac{2}{\sqrt{5}}$ . (The negative root does not lie in the interval $0 \le x \le 1$ .)

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & $\dfrac{2}{\sqrt{5}}$ & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & p & & 2 & & $2 \sqrt{5}$ & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$x = \dfrac{2}{\sqrt{5}}$ gives $y = \dfrac{1}{\sqrt{5}}$ . The dimensions of the rectangle with the largest perimeter are $2 x = \dfrac{4}{\sqrt{5}}$ and $y = \dfrac{1}{\sqrt{5}}$ ; the maximum perimeter is $p = 2 \sqrt{5} \approx 4.47214$ .

67. A window is made in the shape of a rectangle with an isosceles right triangle on top.

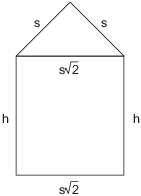
$$\hbox{\epsfysize=1.75 in \epsffile{final-review-11.eps}}$$

(a) Write down an expression for the total area of the window.

(b) Write down an expression for the perimeter of the window (that is, the length of the outside edge).

(c) If the perimeter is given to be 4, what value of s makes the total area a maximum?

(a)

$$A = \dfrac{1}{2} s^2 + \sqrt{2} s h.\quad\halmos$$

(b)

$$p = 2 h + 2 s + \sqrt{2} s.\quad\halmos$$

(c) Since $4 = p = 2 h + 2 s + \sqrt{2}s$ ,

$$h = 2 - s - \dfrac{\sqrt{2}}{2}s.$$

Hence,

$$A = \dfrac{1}{2} s^2 + \sqrt{2} s \left(2 - s - \dfrac{\sqrt{2}}{2} s\right) = \dfrac{1}{2} s^2 + 2 \sqrt{2} s - \sqrt{2} s^2 - s^2 = 2 \sqrt{2} s - \sqrt{2} s^2 - \dfrac{1}{2} s^2.$$

The extreme cases are $s = 0$ and $h = 0$ , which gives $s = \dfrac{4}{2 + \sqrt{2}}$ .

The derivative is

$$\der A s = 2 \sqrt{2} - 2 \sqrt{2} s - s.$$

Find the critical point:

$$\eqalign{ 0 & = 2 \sqrt{2} - 2 \sqrt{2} s - s \cr 2 \sqrt{2} s + s & = 2 \sqrt{2} \cr (2 \sqrt{2} + 1) s & = 2 \sqrt{2} \cr \noalign{\vskip2pt} s & = \dfrac{2 \sqrt{2}}{2 \sqrt{2} + 1} \cr}$$

Plug the critical point and the endpoints into A:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & s & & 0 & & $\dfrac{2 \sqrt{2}}{2 \sqrt{2} + 1}$ & & $\dfrac{4}{2 + \sqrt{2}}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & A & & 0 & & 1.04482 & & 0.68629 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

When $s = \dfrac{2\sqrt{2}}{2\sqrt{2} + 1}$ , the area is a maximum.

68. A cylindrical can with a top and a bottom is to be made with $96 \pi$ square inches of sheet metal with no waste. What values for the radius r and the height h give the can of largest volume?

$$\hbox{\epsfysize=1.5 in \epsffile{final-review-13.eps}}$$

I have

$$V = \pi r^2 h \quad\hbox{and}\quad 96 \pi = 2 \pi r^2 + 2 \pi r h.$$

Solving the second equation for h, I get

$$\eqalign{ 96 \pi & = 2 \pi r^2 + 2 \pi r h \cr 96 \pi - 2 \pi r^2 & = 2 \pi r h \cr \noalign{\vskip2 pt} \dfrac{96 \pi - 2 \pi r^2}{2 \pi r} & = h \cr}$$

Plug this into V:

$$V = \pi r^2 \cdot \dfrac{96 \pi - 2 \pi r^2}{2 \pi r} = \dfrac{1}{2} r(96 \pi - 2 \pi r^2) = 48 \pi r - \pi r^3.$$

Since $r = 0$ is ruled out (as it causes division by 0 in the equation for h), I won't have two endpoints. I will use the Second Derivative Test. I have

$$\eqalign{ \der V r & = 48 \pi - 3 \pi r^2 \cr \noalign{\vskip2 pt} \dfrac{d^2 V}{dr^2} & = -6 \pi r \cr}$$

Find the critical points by setting $\der V r = 0$ and solving:

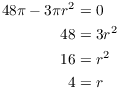
$$\eqalign{ 48 \pi - 3 \pi r^2 & = 0 \cr 48 & = 3 r^2 \cr 16 & = r^2 \cr 4 & = r \cr}$$

(I can throw out $r = -4$ , since the radius can't be negative.) This gives $h = \dfrac{96 \pi - 32 \pi}{8 \pi} = 8$ . In addition.

$$V''(4) = -24 \pi < 0.$$

The critical point is a local max; since it's the only critical point, it's an absolute max.

69. A rectangular box with a square bottom and no top has a volume of 55296 cubic inches. What values of the length x of a side of the bottom and the height y give the box with the smallest total surface area (the area of the bottom plus the area of the sides)?

The area of the 4 sides is $4 x y$ , and the area of the bottom is $x^2$ . So the total area is

$$A = 4 x y + x^2.$$

The volume is

$$55296 = x^2 y.$$

Solving for y gives

$$y = \dfrac{55296}{x^2}.$$

Plug this into A and simplify:

$$A = 4 x \cdot \dfrac{55296}{x^2} + x^2 = \dfrac{221184}{x} + x^2.$$

Note that $x \ne 0$ , since $x = 0$ plugged into $55296 = x^2 y$ gives $55296 = 0$ , a contradiction. So the only restriction on x is that $x > 0$ .

Since x is not restricted to a closed interval $[a, b]$ , I'll use the Second Derivative Test.

Compute the derivatives:

$$A' = -\dfrac{221184}{x^2} + 2 x,$$

$$A'' = \dfrac{442368}{x^3} + 2.$$

Find the critical points:

$$\eqalign{ -\dfrac{221184}{x^2} + 2 x & = 0 \cr \noalign{\vskip2 pt} 2 x & = \dfrac{221184}{x^2} \cr \noalign{\vskip2pt} 2 x^3 & = 221184 \cr x^3 & = 110592 \cr x & = 48 \cr}$$

$x = 48$ gives

$$y = \dfrac{55296}{2304} = 24.$$

Plug $x = 48$ into the Second Derivative:

$$A''(48) = \dfrac{442368}{110592} + 2 = 6 > 0.$$

$x = 48$ is a local min, but it's the only critical point, so it's an absolute min.

70. (a) Find the absolute max and the absolute min of $y = x^3 - 12 x + 5$ on the interval $0 \le x \le 5$ .

(b) Find the absolute max and the absolute min of $f(x) = \dfrac{3}{4}x^{4/3} - 15 x^{1/3}$ on the interval $-1 \le x \le 8$ .

(a) The derivative is

$$y' = 3 x^2 - 12 = 3(x^2 - 4) = 3(x - 2)(x + 2).$$

$y' = 0$ for $x = 2$ and $x = -2$ ; however, only $x = 2$ is in the interval $0 \le x \le 5$ . $y'$ is defined for all x.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 2 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & y & & 5 & & -11 & & 70 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The absolute max is at $x = 5$ ; the absolute min is at $x = 2$ .

(b)

$$f'(x) = x^{1/3} - 5 x^{-2/3} = \dfrac{x - 5}{x^{2/3}}.$$

$f' = 0$ for $x = 5$ and $f'$ is undefined for $x = 0$ . Both points are in the interval.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & -1 & & 8 & & 0 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $f(x)$ & & 15.75 & & -18 & & 0 & & -19.23723 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The absolute max is at $x = -1$ and the absolute min is at $x = 5$ .

71. Use a limit of a rectangle sum to find the exact area under $y = x^2 + 3 x$ from $x = 0$ to $x = 1$ .

Divide the interval $0 \le x \le 1$ up into n equal subintervals. Each subinterval has length $\Delta x = \dfrac{1}{n}$ . I'll evaluate the function at the right-hand endpoints of the subintervals, which are

$$\dfrac{1}{n}, \dfrac{2}{n}, \dfrac{3}{n}, \ldots, \dfrac{n - 1}{n}, \dfrac{n}{n}.$$

The function values are

$$\left(\dfrac{1}{n}\right)^2 + 3\left(\dfrac{1}{n}\right), \left(\dfrac{2}{n}\right)^2 + 3\left(\dfrac{2}{n}\right), \ldots \left(\dfrac{n}{n}\right)^2 + 3\left(\dfrac{n}{n}\right).$$

The sum of the rectangle area is

$$\sum_{k=1}^n \left[\left(\dfrac{k}{n}\right)^2 + 3\left(\dfrac{k}{n}\right)\right]\cdot \dfrac{1}{n} = \dfrac{1}{n^3} \sum_{k=1}^n k^2 + \dfrac{3}{n^2} \sum_{k=1}^n k = \dfrac{1}{n^3} \cdot \dfrac{n(n + 1)(2 n + 1)}{6} + \dfrac{3}{n^2} \cdot \dfrac{n(n + 1)}{2}.$$

The exact area is

$$\lim_{n\to \infty} \left(\dfrac{1}{n^3} \cdot \dfrac{n(n + 1)(2 n + 1)}{6} + \dfrac{3}{n^2} \cdot \dfrac{n(n + 1)}{2}\right) = \dfrac{1}{3} + \dfrac{3}{2} = \dfrac{11}{6}.\quad\halmos$$

72. (a) Compute $\displaystyle \der {} x \int_4^{x^6} \sqrt{2 + t^2}\,dt$ .

(b) Compute $\displaystyle \int \left(\der {} x {\root 3 \of {x^2 + 1}}\right)\,dx$ .

(a)

$$\der {} x \int_4^{x^6} \sqrt{2 + t^2}\,dt = \der {x^6}{x} \der {} {x^6} \int_4^{x^6} \sqrt{2 + t^2}\,dt = (6 x^5) \sqrt{2 + (x^6)^2} = 6 x^5 \sqrt{2 + x^{12}}.\quad\halmos$$

(b)

$$\int \left(\der {} x {\root 3 \of {x^2 + 1}}\right)\,dx = \root 3 \of {x^2 + 1} + C.\quad\halmos$$

73. Use the definition of the derivative as a limit to prove that $\der {} x \dfrac{1}{x - 4} = -\dfrac{1}{(x - 4)^2}$ .

$$f'(x) = \lim_{h\to 0} \dfrac{f(x + h) - f(x)}{h} = \lim_{h\to 0} \dfrac{\dfrac{1}{x + h - 4} - \dfrac{1}{x - 4}}{h} = \lim_{h\to 0} \dfrac{\dfrac{x - 4}{(x - 4)(x + h - 4)} - \dfrac{x + h - 4}{(x - 4)(x + h - 4)}}{h} =$$

$$\lim_{h\to 0} \dfrac{\dfrac{(x - 4) - (x + h - 4)} {(x - 4)(x + h - 4)}}{h} = \lim_{h\to 0} \dfrac{\dfrac{-h}{(x - 4)(x + h - 4)}}{h} = \lim_{h\to 0} \dfrac{-h}{h(x - 4)(x + h - 4)} =$$

$$\lim_{h\to 0} \dfrac{-1}{(x - 4)(x + h - 4)} = -\dfrac{1}{(x - 4)^2}.\quad\halmos$$

74. Compute $\displaystyle \lim_{h\to 0} \dfrac{1}{h} \int_x^{x+h} \sqrt{t^4 + 1}\,dt$ .

Hint: Write the limit as a difference quotient that gives the derivative of a certain function.

The limit as h goes to 0, the $\dfrac{1}{h}$ , and the limits x and $x + h$ remind me of the definition of the derivative. So I make a guess that the limit in the problem is actually the derivative of a function. The problem is to figure out what function is being differentiated ....

Let $\displaystyle f(x) = \int_0^x \sqrt{t^4 + 1}\,dt$ . Then

$$f(x + h) - f(x) = \int_0^{x + h} \sqrt{t^4 + 1}\,dt - \int_0^x \sqrt{t^4 + 1}\,dt = \int_0^{x + h} \sqrt{t^4 + 1}\,dt + \int_x^0 \sqrt{t^4 + 1}\,dt = \int_x^{x+h} \sqrt{t^4 + 1}\,dt.$$

Therefore,

$$\lim_{h\to 0} \dfrac{1}{h} \int_x^{x+h} \sqrt{t^4 + 1}\,dt = \lim_{h\to 0} \dfrac{1}{h} (f(x + h) - f(x)) = \lim_{h\to 0} \dfrac{f(x + h) - f(x)}{h} = f'(x) =$$

$$\der {} x \int_0^x \sqrt{t^4 + 1}\,dt = \sqrt{x^4 + 1}.\quad\halmos$$

75. Let

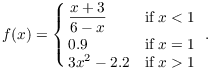
$$f(x) = \cases{\dfrac{x + 3}{6 - x} & if $x < 1$ \cr \noalign{\vskip2 pt} 0.9 & if $x = 1$ \cr 3 x^2 - 2.2 & if $x > 1$ \cr}.$$

Is f continuous at $x = 1$ ? Why or why not?

$$\lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} \dfrac{x + 3}{6 - x} = \dfrac{4}{5} = 0.8.$$

$$\lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} (3 x^2 - 2.2) = 3 - 2.2 = 0.8.$$

The left and right-hand limits agree. Therefore,

$$\lim_{x \to 1} f(x) = 0.8.$$

However, $f(1) = 0.9$ , so $\displaystyle \lim_{x \to 1} f(x) \ne f(1)$ . Hence, f is not continuous at $x = 1$ .

76. Suppose that $f(3) = 5$ and $f'(x) = \dfrac{x^2}{x^2 + 16}$ . Use differentials to approximate $f(2.99)$ to 5 places.

Use

$$f(x + dx) \approx f(x) + f'(x)\,dx.$$

$dx = 2.99 - 3 = -0.01$ and $f'(3) = \dfrac{9}{25} = 0.36$ . Therefore,

$$f(2.99) \approx f(3) + f'(3)\,dx = 5 + (0.36)(-0.01) = 4.99640.\quad\halmos$$

77. A differentiable function satisfies $\der y x = e^x \cos 3 x$ and $y(0) = 0.1$ . Use differentials to approximate $y(0.02)$ .

$dx = 0.02 - 0 = 0.02$ ; when $x = 0$ , $\der y x = e^0 \cos 0 = 1$ . Therefore,

$$dy = \der y x\,dx = (1)(0.02) = 0.02.$$

Hence,

$$y(0.02) \approx y(0) + dy = 0.1 + 0.02 = 0.12.\quad\halmos$$

78. Use 3 iterations of Newton's method starting at $x = 2$ to approximate a solution to $4 - x^2 = e^x$ .

Write the equation as $4 - x^2 - e^x = 0$ . Set $f(x) = 4 - x^2 - e^x$ , so $f'(x) = -2 x - e^x$ .

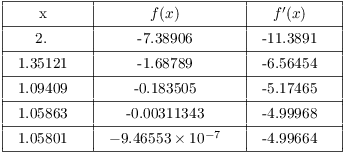
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & x & & $f(x)$ & & $f'(x)$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2. & & -7.38906 & & -11.3891 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1.35121 & & -1.68789 & & -6.56454 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1.09409 & & -0.183505 & & -5.17465 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1.05863 & & -0.00311343 & & -4.99968 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1.05801 & & $-9.46553\times 10^{-7}$ & & -4.99664 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The solution is approximately $x \approx 1.058$ .

79. Suppose that f is a differentiable function, $f(8) = 3$ , and

$$f'(x) > 7 \quad\hbox{for all}\quad x.$$

Prove that $f(10) > 17$ .

Apply the Mean Value Theorem to f on the interval $8 \le x \le 10$ :

$$\dfrac{f(10) - f(8)}{10 - 8} = f'(c) \quad\hbox{for}\quad 8 < c < 10.$$

Then

$$\eqalign{ \dfrac{f(10) - 3}{2} = f'(c) & > 7 \cr \noalign{\vskip2 pt} f(10) - 3 & > 14 \cr f(10) & > 17 \quad\halmos \cr}$$

80. Prove that the function $f(x) = x^3 + 2 x - \cos x + 5$ has exactly one root.

First,

$$f(0) = 4 > 0 \quad\hbox{and}\quad f\left(-\dfrac{\pi}{2}\right) = -\dfrac{27\pi}{8} - \pi + 5 < 0.$$

By the Intermediate Value Theorem, f has at least one root between $-\dfrac{\pi}{2}$ and 0.

Suppose f has more than one root. Then f has at least two roots, so let a and b be two roots of f. By Rolle's theorem, f has a critical point between a and b.

However,

$$f'(x) = 3 x^2 + 2 + \sin x.$$

Since $\sin x \ge -1$ , $2 + \sin x \ge 1$ . But $3 x^2 \ge 0$ , so

$$f'(x) = 3 x^2 + 2 + \sin x \ge 0 + 1 = 1 > 0.$$

Thus, f has no critical points. Therefore, it can't have more than one root.

It follows that f has exactly one root.

The best thing for being sad is to learn something. - Merlyn, in T. H. White's The Once and Future King

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga