Review Problems for Test 1

Math 161

These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the absence of a topic does not imply that it won't appear on the test.

1. Compute $\displaystyle \lim_{x \to 9} \dfrac{x^2 - 81}{x - 9}$ .

2. Compute $\displaystyle \lim_{x \to 2} \dfrac{x^2 - 4}{x^2 - x - 2}$ .

3. Compute $\displaystyle \lim_{x \to 3} \dfrac{x^2 + 2 x - 3}{x^2 - 9}$ .

4. Compute $\displaystyle \lim_{x \to 3-} \dfrac{x^2 + 2 x - 3}{x^2 - 9}$ .

5. Compute $\displaystyle \lim_{x \to +\infty} \dfrac{3 x^7 - 5 x^4 + x - 2}{10 - 2 x^4 - 3 x^7}$ .

6. Compute $\displaystyle \lim_{x \to +\infty} \dfrac{3 x^7 - 5 x^4 + x - 2}{10 - 2 x^4 - 3 x^6}$ .

7. Compute $\displaystyle \lim_{x \to +\infty} (2 x^3 + 5 x + 1)$ .

8. Compute $\displaystyle \lim_{x \to -\infty} (4 - 2 x^2 - x^3)$ .

9. Compute $\displaystyle \lim_{x \to +\infty} \dfrac{4 x^{-11} + 7 x^{-8}}{13 x^{-8} + 5 x^{-9}}$ .

10. Compute $\displaystyle \lim_{x \to 1} \dfrac{x - 1}{\sqrt{x} - 1}$ .

11. Compute 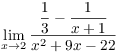$\displaystyle \lim_{x \to 2} \dfrac{\dfrac{1}{3} - \dfrac{1}{x + 1}}{x^2 + 9 x - 22}$ .

12. Compute $\displaystyle \lim_{x \to 2} \root 5 \of {\dfrac{2 x + 5}{x - 7}}$ .

13. Compute 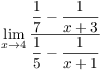$\displaystyle \lim_{x \to 4} \dfrac{\dfrac{1}{7} - \dfrac{1}{x + 3}}{\dfrac{1}{5} - \dfrac{1}{x + 1}}$ .

14. Compute $\displaystyle \lim_{x \to 3} \dfrac{\sqrt{x + 13} - 4}{x^2 + 2 x - 15}$ .

15. Compute $\displaystyle \lim_{x \to 0} \dfrac{7 x \cos 5 x}{8 x + 3 \sin 3 x}$ .

16. Compute $\displaystyle \lim_{x \to 0} \dfrac{3 x + 4 \sin 3 x}{\tan 5 x - x \cos 2 x}$ .

17. Suppose

$f(x) = \cases{ 6 & if $x \le 3$ \cr \noalign{\vskip2pt} \dfrac{x^2 - 9}{x - 3} & if $x > 3$ \cr}$

Determine whether $\displaystyle \lim_{x \to 3} f(x)$ is defined. If it is, compute it.

18. Compute $\displaystyle \lim_{x \to 0} x^4 \cos \dfrac{1}{x^2}$ .

19. Suppose that

$\lim_{x \to 2} g(x) = 3, \quad \lim_{x \to 2} h(x) = 9,$

$(x^2 + 8) g(x) \le f(x) \le (x + 2) h(x) \quad\hbox{for all}\quad x.$

Compute $\displaystyle \lim_{x \to 2} f(x)$ .

20. The picture below shows that graph of a function .

$\hbox{\epsfysize=2.5 in \epsffile{rev1-2.eps}}$

Compute:

(a) $\displaystyle \lim_{x \to 2-} f(x)$ .

(b) $\lim_{x \to 2+} f(x)$ .

(d) $\lim_{x \to 3-} f(x)$ .

(e) $\lim_{x \to 3+} f(x)$ .

(f) $\lim_{x \to 3} f(x)$ .

(g) .

21. Locate the horizontal asymptotes and the vertical asymptotes of

$y = \dfrac{x^2}{x^3 - 5 x^2 - 6 x}.$

Justify your answer by computing the relevant limits.

22. Differentiate .

23. Differentiate $f(x) = \dfrac{4}{x^3} - \dfrac{2}{\sqrt{x}}$ .

24. Differentiate $y = 3{\root 7 \of {x^2}} - 6{\root 5 \of {42}}$ .

25. Differentiate $g(u) = (u^5 - u^4 + u^3 + u^2 + u + 1)^{42}$ .

26. Differentiate $h(x) = \left(\sqrt{x} + x - x^2\right)(x^6 + x^3 + x + 1)$ .

27. Differentiate $y = \dfrac{x^6 + x^3 + 1}{x^4 + x^2 + 1}$ .

28. Differentiate $f(x) = \left(3 + \left(3 + x^{-2}\right)^{-2}\right)^{-2}$ .

29. Differentiate $f(x) = (\sin 3 x + \tan 5 x)^{50}$ .

30. Differentiate $g(t) = \sin(\cos(\tan t)) + \sec\left(\dfrac{t}{\tan t}\right)$ .

31. Differentiate $y = \sin(\cos x) + (\sin x)(\cos x)$ .

32. Find $\der {} x \left(\dfrac{x^7}{13} + 65 x + \dfrac{4}{x^2} + 3\right)$ .

33. Find $\der {} x \left(\sqrt{3 x} + \dfrac{7}{\root 3 \of x} + {\root 7 \of {x^2}}\right)$ .

34. Compute $\der {} x \left[\cos (3 x + 1)^2 + (\cos (3 x + 1))^2\right]$ .

35. Compute $\der {} x \dfrac{6 x^3 + 3\sin x}{17}$ .

36. Find $\der {} x (3\sin x - 7 x)(4 + x^2 - \tan x)$ .

37. Find if $f(t) = \dfrac{3}{(t^2 + 3 t + 1)^5}$ .

38. Compute $\der {} x (e^{3 x} + 1)(\sin 2 x)(x^4 + 2 x + 1)$ .

39. Find $\der {} x \left(\dfrac{\sqrt{x} + \sec x}{3 + 5 x - \cos x}\right)$ .

40. Find if $y = \dfrac{(2 - 3 x - x^5)e^{4 x}}{\tan 5 x + 7}$ .

41. Compute $\der {} x \dfrac{1 + \csc (x^2)}{(e^{-7 x} + 3 x)(7 x^6 + x + 1)}$ .

42. Compute $\der {} x \left(\dfrac{x^2 + x + 1}{x^3 - 3 x + 5}\right)^{11}$ .

43. Compute $\der {} x \left(e^{x^2} + 7^{x^2} + e^{7 x} + 7^{e^x}\right)$ .

44. Compute $\der {} x \root 3 \of {(x^2 + e^x)(\ln x + 42 x) + x^3}$ .

45. Compute $\der {} w \ln \sqrt{e^{w^2} + e^{2 w} + 1}$ .

46. Compute $\der {} x \left(x^3 + \left(x^3 + (x^3 + 1)^3\right)^3\right)^3$ .

47. Compute $\der {} x \left(\dfrac{2 x + 5}{(x + 2)^3}\right)$ .

48. Compute the derivative with respect to t of $s(t) = \sec \left(\dfrac{5}{t^3 + 5 t + 8}\right)$ .

49. Compute $\der {} x [\log_5 (x^2 + x + 1)]^7$ .

50. Compute for .

51. Compute $y^{(50)}$ if $y = \dfrac{1}{4 - x}$ .

52. Compute $\der {} x \sqrt{e^{f(x)^2} + 1}$ .

53. Compute $\der {} x \ln(\sin (g(x)) + 1)$ .

54. f and g are differentiable functions. The values of f, g, , and at and are shown below:

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & $f(x)$ & & $g(x)$ & & $f'(x)$ & & $g'(x)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & -6 & & 5 & & 4 & & 10 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 5 & & 0.5 & & -1 & & 7 & & -3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

Compute , $\left(\dfrac{f}{g}\right)'(2)$ , and .

55. Find the equation of the tangent line to the graph of at .

56. Find the equation of the tangent line to the graph of $y = \dfrac{1}{(x^2 + 4 x + 5)^2}$ at .

57. For what value or values of c does the tangent line to the graph of at pass through the point ?

58. The position of a cheeseburger at time t is given by

Find the value(s) of t for which the velocity is 0. Find the value(s) of t for which the acceleration is 0.

59. For what values of x is the function $f(x) = \dfrac{x - 5}{x^2 - 3 x - 10}$ continuous?

60. For what values of x is the function $f(x) = \dfrac{1}{\sqrt{x^2 + 5 x + 6}}$ continuous?

61. Let

$f(x) = \cases{ \dfrac{x^2 - 7 x - 8}{x + 1} & if $x \ne -1$ \cr \noalign{\vskip2pt} 9& if $x = -1$ \cr}$

Prove or disprove: f is continuous at .

62. Find the value of c which makes the following function continuous at :

$f(x) = \cases{ 1 + 3 x - c x^2 & if $x < 2$ \cr 7 x + 3 & if $x \ge 2$ \cr}.$

63. Prove that has a root between and .

64. Suppose f is continuous, , and . Prove that there is a number x between 2 and 5 such that $x^3 \cdot f(x) = 110$ .

65. Suppose $f(x) = \sqrt{x - 6}$ . Use the limit definition of the derivative to compute .

66. Suppose $f(x) = \dfrac{1}{x + 3}$ . Use the limit definition of the derivative to compute .

67. Suppose $f(x) = \dfrac{1}{\sqrt{x} + 1}$ . Use the limit definition of the derivative to compute .

68. The graph of a function is pictured below. For what values of x is f continuous but not differentiable? For what values of f is f not continuous?

$\hbox{\epsfysize=2.5 in \epsffile{rev1-1.eps}}$

69. (a) Find the average rate of change of on the interval $1 \le x \le 3$ .

(b) Find the instantaneous rate of change of at .

70. Give an example of a function which is defined for all x and a number c such that

$\lim_{x \to c} f(x) \ne f(c).$

71. Suppose $f(x) = \dfrac{x + 1}{x + 2}$ . Find $f^{-1}(x)$ .

72. Suppose and . Find $(f^{-1})'(5)$ .

73. Suppose and $f'(x) = \sqrt{x^4 + x^2 + 16}$ . Find $(f^{-1})'(5)$ .

74. Suppose $f(x) = (x^5 + 2 x^3 + 5)^{1/3}$ . Find $(f^{-1})'(2)$ .

75. Compute $\der {} x (x^2 + 3 x + 1)^{(x^2+6)}$ .

76. Compute $\der {} x (e^x + 1)^{\sin x}$ .

77. Find the equation of the tangent line to at .

78. (An alternate approach to logarithmic differentiation)

(a) Use the identity $A = e^{\ln A}$ to write $(x^2 + 1)^{\tan x}$ using $e^{(\cdot)}$ and $\ln {(\cdot)}$ .

(b) Use the Chain Rule to differentiate the expression you obtained in (a). (This gives another way of doing logarithmic differentiation involving powers.)

79. Find if y is defined implicitly by

$\sin x + \cos y = 3 x + 5 y.$

80. Find the equation of the tangent line to the curve

$x^3 + 2 x y^3 = x^2 - y^2 + 3 \quad\hbox{at the point}\quad (1,1).$

81. Find the equation of the tangent line to the curve

$\dfrac{x^2}{y} + y^2 = 7 x - 2 y - 9 \quad\hbox{at the point}\quad (3, 1).$

82. Find at the point on the curve

Solutions to the Review Problems for Test 1

1. Compute $\displaystyle \lim_{x \to 9} \dfrac{x^2 - 81}{x - 9}$ .

Plugging in gives $\dfrac{0}{0}$ . I factor the top, then cancel common factors of :

$\lim_{x \to 9} \dfrac{x^2 - 81}{x - 9} = \lim_{x \to 9} \dfrac{(x - 9)(x + 9)}{x - 9} = \lim_{x \to 9} (x + 9) = 18.\quad\halmos$

2. Compute $\displaystyle \lim_{x \to 2} \dfrac{x^2 - 4}{x^2 - x - 2}$ .

Since plugging in gives $\dfrac{0}{0}$ , it is reasonable to suppose that the zeros are being caused by a common factor on the top and the bottom. So factor the top and the bottom and cancel the 's:

$\lim_{x \to 2} \dfrac{x^2 - 4}{x^2 - x - 2} = \lim_{x \to 2} \dfrac{(x - 2)(x + 2)}{(x - 2)(x + 1)} = \lim_{x \to 2} \dfrac{x + 2}{x + 1} = \dfrac{4}{3}. \quad\halmos$

3. Compute $\displaystyle \lim_{x \to 3} \dfrac{x^2 + 2 x - 3}{x^2 - 9}$ .

$\lim_{x \to 3} \dfrac{x^2 + 2 x - 3}{x^2 - 9} \quad\hbox{is undefined}.$

If I plug in , I get $\dfrac{12}{0}$ , a nonzero number over 0. In this case, the limit does not exist.

(By the way, I hope you didn't try to use L'H\^opital's Rule here. It doesn't apply.)

4. Compute $\displaystyle \lim_{x \to 3-} \dfrac{x^2 + 2 x - 3}{x^2 - 9}$ .

$\lim_{x \to 3-} \dfrac{x^2 + 2 x - 3}{x^2 - 9} = -\infty.$

This problem is different from the previous one because x is approaching 3 from the left. It would not be incorrect to say that the limit is undefined, but it is better to say that the limit is $-\infty$ . There is a vertical asymptote at , and the graph goes downward (to $-\infty$ ) as it approaches the asymptote from the left.

How do you see algebraically that this is what it does? One way is to plug numbers close to 3, but less than 3, into $\dfrac{x^2 + 2 x - 3}{x^2 - 9}$ . For example, if , $\dfrac{x^2 + 2 x - 3}{x^2 - 9} \approx -199999$ --- a big negative number. This doesn't prove that it's going to $-\infty$ , but it's pretty good evidence.

Here is how I can analyze it. I know that plugging in gives $\dfrac{12}{0}$ . Therefore, I should be getting either $+\infty$ or $-\infty$ --- the reciprocal of something small ( $\approx 0$ ) should be something big.

Now let x approach 3 from the left. surely goes to 12, a positive number. goes to 0, but since , will be negative. Now $\dfrac{\rm positive}{\rm negative} = {\rm negative}$ , so the answer is $-\infty$ .

5. Compute $\displaystyle \lim_{x \to +\infty} \dfrac{3 x^7 - 5 x^4 + x - 2}{10 - 2 x^4 - 3 x^7}$ .

The idea is to divide the top and bottom by the highest power of x that occurs in either --- in this case, . Then use the fact that

$\lim_{x \to \pm \infty} \dfrac{\rm number}{x^{\eightrm positive power}} = 0.$

I have

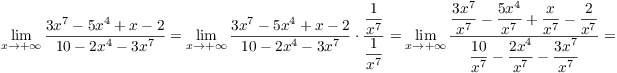
$\lim_{x \to +\infty} \dfrac{3 x^7 - 5 x^4 + x - 2}{10 - 2 x^4 - 3 x^7} = \lim_{x \to +\infty} \dfrac{3 x^7 - 5 x^4 + x - 2}{10 - 2 x^4 - 3 x^7} \cdot \dfrac{\dfrac{1}{x^7}}{\dfrac{1}{x^7}} = \lim_{x \to +\infty} \dfrac{\dfrac{3 x^7}{x^7} - \dfrac{5 x^4}{x^7} + \dfrac{x}{x^7} - \dfrac{2}{x^7}}{\dfrac{10}{x^7} - \dfrac{2 x^4}{x^7} - \dfrac{3 x^7}{x^7}} =$

$\lim_{x \to +\infty} \dfrac{3 - \dfrac{5}{x^3} + \dfrac{1}{x^6} - \dfrac{2}{x^7}}{\dfrac{10}{x^7} - \dfrac{2}{x^3} - 3} = \dfrac{3 - 0 + 0 - 0}{0 - 0 - 3} = -1. \quad\halmos$

6. Compute $\displaystyle \lim_{x \to +\infty} \dfrac{3 x^7 - 5 x^4 + x - 2}{10 - 2 x^4 - 3 x^6}$ .

$\lim_{x \to +\infty} \dfrac{3 x^7 - 5 x^4 + x - 2}{10 - 2 x^4 - 3 x^6} = \lim_{x \to +\infty} \dfrac{3 x^7 - 5 x^4 + x - 2}{10 - 2 x^4 - 3 x^6} \cdot \dfrac{\dfrac{1}{x^7}}{\dfrac{1}{x^7}} = \lim_{x \to +\infty} \dfrac{\dfrac{3 x^7}{x^7} - \dfrac{5 x^4}{x^7} + \dfrac{x}{x^7} - \dfrac{2}{x^7}}{\dfrac{10}{x^7} - \dfrac{2 x^4}{x^7} - \dfrac{3 x^6}{x^7}} =$

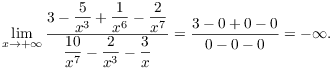
$\lim_{x \to +\infty} \dfrac{3 - \dfrac{5}{x^3} + \dfrac{1}{x^6} - \dfrac{2}{x^7}}{\dfrac{10}{x^7} - \dfrac{2}{x^3} - \dfrac{3}{x}} = \dfrac{3 - 0 + 0 - 0}{0 - 0 - 0} = -\infty.$

There's little question that the limit is undefined; why is it $-\infty$ ? One approach is to note that the top and bottom are dominated by the highest powers of x. So this limits looks like

$\lim_{x \to +\infty} \dfrac{3 x^7}{-3 x^6} = \lim_{x \to +\infty} -x = -\infty.$

As a check, if you plug into $\dfrac{3 x^7 - 5 x^4 + x - 2}{10 - 2 x^4 - 3 x^6}$ , you get (approximately) .

7. Compute $\displaystyle \lim_{x \to +\infty} (2 x^3 + 5 x + 1)$ .

As $x \to +\infty$ , I have $2 x^3 \to +\infty$ and $5 x \to +\infty$ . So

$\lim_{x \to +\infty} (2 x^3 + 5 x + 1) = +\infty.\quad\halmos$

8. Compute $\displaystyle \lim_{x \to -\infty} (4 - 2 x^2 - x^3)$ .

As $x \to +\infty$ , I have $2 x^3 \to +\infty$ and $5 x \to +\infty$ . So

$\lim_{x \to +\infty} (2 x^3 + 5 x + 1) = +\infty.\quad\halmos$

9. Compute $\displaystyle \lim_{x \to +\infty} \dfrac{4 x^{-11} + 7 x^{-8}}{13 x^{-8} + 5 x^{-9}}$ .

$\lim_{x \to +\infty} \dfrac{4 x^{-11} + 7 x^{-8}}{13 x^{-8} + 5 x^{-9}} = \lim_{x \to +\infty} \dfrac{\dfrac{4}{x^{11}} + \dfrac{7}{x^8}}{\dfrac{13}{x^8} + \dfrac{5}{x^9}} = \lim_{x \to +\infty} \dfrac{\dfrac{4}{x^{11}} + \dfrac{7}{x^8}}{\dfrac{13}{x^8} + \dfrac{5}{x^9}} \cdot \dfrac{\vphantom{\dfrac{x}{x}} x^8}{\vphantom{\dfrac{x}{x}} x^8} =$

$\lim_{x \to +\infty} \dfrac{\dfrac{4 x^8}{x^{11}} + \dfrac{7 x^8}{x^8}}{\dfrac{13 x^8}{x^8} + \dfrac{5 x^8}{x^9}} = \lim_{x \to +\infty} \dfrac{\dfrac{4}{x^3} + 7}{13 + \dfrac{5}{x}} = \dfrac{0 + 7}{13 + 0} = \dfrac{7}{13}.\quad\halmos$

10. Compute $\displaystyle \lim_{x \to 1} \dfrac{x - 1}{\sqrt{x} - 1}$ .

Method 1. Multiply the top and bottom by the conjugate:

$\lim_{x \to 1} \dfrac{x - 1}{\sqrt{x} - 1} = \lim_{x \to 1} \dfrac{x - 1}{\sqrt{x} - 1} \cdot \dfrac{\sqrt{x} + 1}{\sqrt{x} + 1} = \lim_{x \to 1} \dfrac{(x - 1)(\sqrt{x} + 1)}{(\sqrt{x} - 1)(\sqrt{x} + 1)} =$

$\lim_{x \to 1} \dfrac{(x - 1)(\sqrt{x} + 1)}{x - 1} = \lim_{x \to 1} (\sqrt{x} + 1) = 1 + 1 = 2.$

Method 2. Factor the top:

$\lim_{x \to 1} \dfrac{x - 1}{\sqrt{x} - 1} = \lim_{x \to 1} \dfrac{(\sqrt{x} - 1)(\sqrt{x} + 1)}{\sqrt{x} - 1} = \lim_{x \to 1} (\sqrt{x} + 1) = 1 + 1 = 2.\quad\halmos$

11. Compute 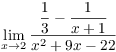$\displaystyle \lim_{x \to 2} \dfrac{\dfrac{1}{3} - \dfrac{1}{x + 1}}{x^2 + 9 x - 22}$ .

$\lim_{x \to 2} \dfrac{\dfrac{1}{3} - \dfrac{1}{x + 1}}{x^2 + 9 x - 22} = \lim_{x \to 2} \dfrac{\dfrac{1}{3} - \dfrac{1}{x + 1}}{(x + 11)(x - 2)} = \lim_{x \to 2} \dfrac{\dfrac{1}{3} - \dfrac{1}{x + 1}}{(x + 11)(x - 2)} \cdot \dfrac{\vbox{\vphantom{$\dfrac{x}{x}$}} 3 (x + 1)}{\vbox{\vphantom{$\dfrac{x}{x}$}} 3 (x + 1)} =$

$\lim_{x \to 2} \dfrac{\dfrac{3(x + 1)}{3} - \dfrac{3(x + 1)}{x + 1}}{3 (x + 1)(x + 11)(x - 2)} = \lim_{x \to 2} \dfrac{x + 1 - 3}{3 (x + 1)(x + 11)(x - 2)} = \lim_{x \to 2} \dfrac{x - 2}{3 (x + 1)(x + 11)(x - 2)} = \lim_{x \to 2} \dfrac{1}{3 (x + 1)(x + 11)} = \dfrac{1}{117}.\quad\halmos$

12. Compute $\displaystyle \lim_{x \to 2} \root 5 \of {\dfrac{2 x + 5}{x - 7}}$ .

$\lim_{x \to 2} \root 5 \of {\dfrac{2 x + 5}{x - 7}} = \root 5 \of {-\dfrac{9}{5}}.$

Nothing complicated is going on here --- I just plug in . (By the way --- Do you know how to compute $\root 5 \of {-\dfrac{9}{5}}$ on your calculator? It's approximately -1.12475. You should always give exact answers unless told otherwise, however.)

13. Compute $\displaystyle \lim_{x \to 4} \dfrac{\dfrac{1}{7} - \dfrac{1}{x + 3}}{\dfrac{1}{5} - \dfrac{1}{x + 1}}$ .

$\lim_{x \to 4} \dfrac{\dfrac{1}{7} - \dfrac{1}{x + 3}} {\dfrac{1}{5} - \dfrac{1}{x + 1}} = \lim_{x \to 4} \dfrac{\dfrac{1}{7} - \dfrac{1}{x + 3}} {\dfrac{1}{5} - \dfrac{1}{x + 1}} \cdot \dfrac{(5)(7)(x + 3)(x + 1)}{(5)(7)(x + 3)(x + 1)} = \lim_{x \to 4} \dfrac{5(x + 1)\left(\dfrac{7(x + 3)}{7} - \dfrac{7(x + 3)}{x + 3}\right)} {7(x + 3)\left(\dfrac{5(x + 1)}{5} - \dfrac{5(x + 1)}{x + 1}\right)} =$

$\lim_{x \to 4} \dfrac{5(x + 1)[(x + 3) - 7]}{7(x + 3)[(x + 1) - 5]} = \lim_{x \to 4} \dfrac{5(x + 1)(x - 4)}{7(x + 3)(x - 4)} = \lim_{x \to 4} \dfrac{5(x + 1)}{7(x + 3)} = \dfrac{25}{49}.\quad\halmos$

14. Compute $\displaystyle \lim_{x \to 3} \dfrac{\sqrt{x + 13} - 4}{x^2 + 2 x - 15}$ .

$\lim_{x \to 3} \dfrac{\sqrt{x + 13} - 4}{x^2 + 2 x - 15} = \lim_{x \to 3} \dfrac{\sqrt{x + 13} - 4}{(x + 5)(x - 3)} = \lim_{x \to 3} \dfrac{\sqrt{x + 13} - 4}{(x + 5)(x - 3)} \cdot \dfrac{\sqrt{x + 13} + 4}{\sqrt{x + 13} + 4} =$

$\lim_{x \to 3} \dfrac{(\sqrt{x + 13})^2 - 4^2}{(x + 5)(x - 3)(\sqrt{x + 13} + 4)} = \lim_{x \to 3} \dfrac{x + 13 - 16}{(x + 5)(x - 3)(\sqrt{x + 13} + 4)} = \lim_{x \to 3} \dfrac{x - 3}{(x + 5)(x - 3)(\sqrt{x + 13} + 4)} =$

$\lim_{x \to 3} \dfrac{1}{(x + 5)(\sqrt{x + 13} + 4)} = \dfrac{1}{64}.\quad\halmos$

15. Compute $\displaystyle \lim_{x \to 0} \dfrac{7 x \cos 5 x}{8 x + 3 \sin 3 x}$ .

Remember that

$\lim_{u \to 0} \dfrac{\sin u}{u} = 1.$

In this problem, I'll let . Now $x \to 0$ if and only if $u = 3 x \to 0$ , so

$\lim_{x \to 0} \dfrac{\sin 3 x}{3 x} = 1.$

Here's the solution:

$\lim_{x \to 0} \dfrac{7 x \cos 5 x}{8 x + 3 \sin 3 x} = \lim_{x \to 0} \dfrac{7 x \cos 5 x}{8 x + 3 \sin 3 x} \cdot \dfrac{\dfrac{1}{x}}{\dfrac{1}{x}} = \lim_{x \to 0} \dfrac{7 \cos 5 x}{8 + 3 \dfrac{\sin 3 x}{x}} = \lim_{x \to 0} \dfrac{7 \cos 5 x}{8 + 9 \left(\dfrac{\sin 3 x}{3 x}\right)} =$

$\dfrac{7 \cdot 1}{8 + 9 \cdot 1} = \dfrac{7}{17}.\quad\halmos$

16. Compute $\displaystyle \lim_{x \to 0} \dfrac{3 x + 4 \sin 3 x}{\tan 5 x - x \cos 2 x}$ .

$\lim_{x \to 0} \dfrac{3 x + 4 \sin 3 x}{\tan 5 x - x \cos 2 x} = \lim_{x \to 0} \dfrac{3 x + 4 \sin 3 x} {\dfrac{\sin 5 x}{\cos 5 x} - x\cos 2 x} = \lim_{x \to 0} \dfrac{3 x + 4 \sin 3 x} {\dfrac{\sin 5 x}{\cos 5 x} - x \cos 2 x}\cdot \dfrac{\dfrac{1}{x}}{\dfrac{1}{x}} =$

$\lim_{x \to 0} \dfrac{3 + 4 \dfrac{\sin 3 x}{x}} {\dfrac{\sin 5 x}{x}\dfrac{1}{\cos 5 x} - \cos 2 x} = \lim_{x \to 0} \dfrac{3 + 4 \cdot3 \dfrac{\sin 3 x}{3 x}} {5\dfrac{\sin 5 x}{5 x}\dfrac{1}{\cos 5 x} - \cos 2 x} = \dfrac{3 + 12}{5 - 1} = \dfrac{15}{4}.\quad\halmos$

17. Suppose

$f(x) = \cases{ 6 & if $x \le 3$ \cr \noalign{\vskip2pt} \dfrac{x^2 - 9}{x - 3} & if $x > 3$ \cr}$

Determine whether $\displaystyle \lim_{x \to 3} f(x)$ is defined. If it is, compute it.

The function is made of "two pieces" glued together at , I'll compute $\lim_{x \to 3} f(x)$ by computing the limits from the left and right, and seeing if they're equal. (If they aren't equal, the limit is undefined.)

The left-hand limit is

$\lim_{x \to 3-} f(x) = \lim_{x \to 3-} 6 = 6.$

The right-hand limit is

$\lim_{x \to 3+} f(x) = \lim_{x \to 3+} \dfrac{x^2 - 9}{x - 3} = \lim_{x \to 3+} \dfrac{(x - 3)(x + 3)}{x - 3} = \lim_{x \to 3+} (x + 3) = 6.$

Since the left- and right-hand limits are equal, $\lim_{x \to 3} f(x)$ is defined, and

$\lim_{x \to 3} f(x) = 6.\quad\halmos$

18. Compute $\displaystyle \lim_{x \to 0} x^4 \cos \dfrac{1}{x^2}$ .

$\matrix{ -1 & \le & \cos \dfrac{1}{x^2} & \le & 1 \cr \noalign{\vskip2 pt} -x^4 & \le & x^4 \cos \dfrac{1}{x^2} & \le & x^4 \cr}$

Take the limit as $x \to 0$ . I have

$\lim_{x \to 0} x^4 = 0 \quad\hbox{and}\quad \lim_{x \to 0} (-x^4) = 0.$

By the Squeezing Theorem,

$\lim_{x \to 0} x^4 \cos \dfrac{1}{x^2} = 0.\quad\halmos$

19. Suppose that

$\lim_{x \to 2} g(x) = 3, \quad \lim_{x \to 2} h(x) = 9,$

$(x^2 + 8) g(x) \le f(x) \le (x + 2) h(x) \quad\hbox{for all}\quad x.$

Compute $\displaystyle \lim_{x \to 2} f(x)$ .

$\lim_{x \to 2} (x^2 + 8) g(x) = 12 \cdot 3 = 36 \quad\hbox{and}\quad \lim_{x \to 2} (x + 2) h(x) = 4 \cdot 9 = 36.$

By the Squeezing Theorem, $\displaystyle \lim_{x \to 2} f(x) = 36$ .

20. The picture below shows that graph of a function .

$\hbox{\epsfysize=2.5 in \epsffile{rev1-2.eps}}$

Compute:

(a) $\displaystyle \lim_{x \to 2-} f(x)$ .

(b) $\lim_{x \to 2+} f(x)$ .

(d) $\lim_{x \to 3-} f(x)$ .

(e) $\lim_{x \to 3+} f(x)$ .

(f) $\lim_{x \to 3} f(x)$ .

(g) .

(a) $\displaystyle \lim_{x \to 2-} f(x) = 5$ .

(b) $\displaystyle \lim_{x \to 2+} f(x) = 4$ .

(d) $\displaystyle \lim_{x \to 3-} f(x) = 2$ .

(e) $\displaystyle \lim_{x \to 3+} f(x) = 2$ .

(f) $\displaystyle \lim_{x \to 3} f(x) = 2$ .

(g) $\displaystyle f(3) = 3$ .

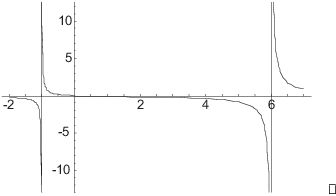
21. Locate the horizontal asymptotes and the vertical asymptotes of

$y = \dfrac{x^2}{x^3 - 5 x^2 - 6 x}.$

Justify your answer by computing the relevant limits.

$\lim_{x \to \infty} \dfrac{x^2}{x^3 - 5 x^2 - 6 x} = 0 \quad\hbox{and}\quad \lim_{x \to -\infty} \dfrac{x^2}{x^3 - 5 x^2 - 6 x} = 0.$

Hence, is a horizontal asymptote at $+\infty$ and at $-\infty$ .

Factor the bottom:

$y = \dfrac{x^2}{x(x - 6)(x + 1)}.$

The function is undefined at , , and at .

Note that

$\lim_{x \to 0} \dfrac{x^2}{x(x - 6)(x + 1)} = \lim_{x \to 0} \dfrac{x}{(x - 6)(x + 1)} = 0.$

Hence, the graph does not have a vertical asymptote at .

Consider the limits at .

I know the one-sided limits will be either $+\infty$ or $-\infty$ , since plugging in gives $\dfrac{36}{0}$ , a nonzero number divided by 0.

Take $x \to 6^+$ as an example. $x^2 \to 36$ , $x \to 6$ , $x + 1 \to 7$ , and $x - 6\to 0$ . In the last case, since , , i.e. goes to 0 through positive numbers. Since all the factors of $\dfrac{x^2}{x(x - 6)(x + 1)}$ are positive as $x \to 6^+$ , the quotient must be positive, and the limit is $+\infty$ .

Similar reasoning works for the left-hand limit.

Thus,

$\lim_{x \to 6^+} \dfrac{x^2}{x(x - 6)(x + 1)} = +\infty \quad\hbox{and}\quad \lim_{x \to 6^+} \dfrac{x^2}{x(x - 6)(x + 1)} = -\infty.$

There is a vertical asymptote at .

Likewise,

$\lim_{x \to -1^+} \dfrac{x^2}{x(x - 6)(x + 1)} = +\infty \quad\hbox{and}\quad \lim_{x \to -1^+} \dfrac{x^2}{x(x - 6)(x + 1)} = -\infty.$

There is a vertical asymptote at .

The results are visible in the graph of the function:

$\hbox{\epsfysize=1.75 in \epsffile{rev1-28.eps}}\quad\halmos$

22. Differentiate .

$f'(x) = 40 x^4 + 8 x - 9.\quad\halmos$

23. Differentiate $f(x) = \dfrac{4}{x^3} - \dfrac{2}{\sqrt{x}}$ .

$f'(x) = -12 x^{-4} + x^{-3/2}.\quad\halmos$

24. Differentiate $y = 3{\root 7 \of {x^2}} - 6{\root 5 \of {42}}$ .

$y' = \dfrac{6}{7} x^{-5/7}.\quad\halmos$

25. Differentiate $g(u) = (u^5 - u^4 + u^3 + u^2 + u + 1)^{42}$ .

$g'(u) = 42(u^5 - u^4 + u^3 + u^2 + u + 1)^{41} (5 u^4 - 4 u^3 + 3 u^2 + 2 u + 1).\quad\halmos$

26. Differentiate $h(x) = \left(\sqrt{x} + x - x^2\right)(x^6 + x^3 + x + 1)$ .

$h'(x) = \left(\sqrt{x} + x - x^2\right)(6 x^5 + 3 x^2 + 1) + (x^6 + x^3 + x + 1)\left(\dfrac{1}{2}x^{-1/2} + 1 - 2 x\right).\quad\halmos$

27. Differentiate $y = \dfrac{x^6 + x^3 + 1}{x^4 + x^2 + 1}$ .

$y' = \dfrac{(x^4 + x^2 + 1)(6 x^5 + 3 x^2) - (x^6 + x^3 + 1)(4 x^3 + 2 x)}{(x^4 + x^2 + 1)^2}.\quad\halmos$

28. Differentiate $f(x) = \left(3 + \left(3 + x^{-2}\right)^{-2}\right)^{-2}$ .

$f'(x) = (-2)\left(3 + \left(3 + x^{-2}\right)^{-2}\right)^{-3} \cdot (-2)\left(3 + x^{-2}\right)^{-3} \cdot (-2) x^{-3}.\quad\halmos$

29. Differentiate $f(x) = (\sin 3 x + \tan 5 x)^{50}$ .

$f'(x) = 50(\sin 3 x + \tan 5 x)^{49}(3 \cos 3 x + 5(\sec 5 x)^2).\quad\halmos$

30. Differentiate $g(t) = \sin(\cos(\tan t)) + \sec\left(\dfrac{t}{\tan t}\right)$ .

$g'(t) = [\cos(\cos(\tan t))] \cdot (-\sin(\tan t)) \cdot (\sec t)^2 + \left(\sec\left(\dfrac{t}{\tan t}\right) \tan\left(\dfrac{t}{\tan t}\right)\right) \left(\dfrac{(\tan t)(1) - (t)(\sec t)^2}{(\tan t)^2}\right).\quad\halmos$

31. Differentiate $y = \sin(\cos x) + (\sin x)(\cos x)$ .

$y' = (\cos(\cos x))\cdot (-\sin x) + \left((\sin x)(-\sin x) + (\cos x)(\cos x)\right).\quad\halmos$

32. Find $\der {} x \left(\dfrac{x^7}{13} + 65 x + \dfrac{4}{x^2} + 3\right)$ .

Note that

$\dfrac{x^7}{13} + 65 x + \dfrac{4}{x^2} + 3 = \dfrac{x^7}{13} + 65 x + 4 x^{-2} + 3.$

Then

$\der {} x \left(\dfrac{x^7}{13} + 65 x + 4 x^{-2} + 3\right) = \dfrac{7}{13}x^6 + 65 - 8 x^{-3} = \dfrac{7}{13}x^6 + 65 - \dfrac{8}{x^3}.\quad\halmos$

33. Find $\der {} x \left(\sqrt{3 x} + \dfrac{7}{\root 3 \of x} + {\root 7 \of {x^2}}\right)$ .

Note that

$\sqrt{3 x} + \dfrac{7}{\root 3 \of x} + {\root 7 \of {x^2}} = \sqrt{3}\sqrt{x} + 7 x^{-1/3} + x^{2/7} = \sqrt{3}\cdot x^{1/2} + 7 x^{-1/3} + x^{2/7}.$

Then

$\der {} x \left(\sqrt{3}\cdot x^{1/2} + 7 x^{-1/3} + x^{2/7}\right) = \dfrac{\sqrt{3}}{2}x^{-1/2} - \dfrac{7}{3}x^{-4/3} + \dfrac{2}{7}x^{-5/7}.\quad\halmos$

34. Compute $\der {} x \left[\cos (3 x + 1)^2 + (\cos (3 x + 1))^2\right]$ .

$\der {} x \left[\cos (3 x + 1)^2 + (\cos (3 x + 1))^2\right] = (-\sin (3 x + 1)^2)(2)(3 x + 1)(3) + 2 (\cos (3 x + 1))(-\sin (3 x + 1))(3) =$

$\hskip0.5 in -6 (3 x + 1) \sin (3 x + 1)^2 - 6 \cos (3 x + 1) \sin (3 x + 1).\quad\halmos$

35. Compute $\der {} x \dfrac{6 x^3 + 3\sin x}{17}$ .

$\der {} x \dfrac{6 x^3 + 3\sin x}{17} = \der {} x \dfrac{1}{17}\left(6 x^3 + 3\sin x\right) = \dfrac{1}{17}\left(18 x^2 + 3\cos x\right).$

It is not a good idea to use the Quotient Rule when either the top or the bottom of a fraction is a number.

36. Find $\der {} x (3\sin x - 7 x)(4 + x^2 - \tan x)$ .

$\der {} x (3\sin x - 7 x)(4 + x^2 - \tan x) = (3\sin x - 7 x)(2 x - (\sec x)^2) + (4 + x^2 - \tan x)(3\cos x - 7).\quad\halmos$

37. Find if $f(t) = \dfrac{3}{(t^2 + 3 t + 1)^5}$ .

Rewrite the function as

$f(t) = 3(t^2 + 3 t + 1)^{-5}.$

Then

$f'(t) = (3)(-5)(t^2 + 3 t + 1)^{-6}(2 t + 3) = -\dfrac{15(2 t + 3)}{(t^2 + 3 t + 1)^6}.$

It is not a good idea to use the Quotient Rule when either the top or the bottom of a fraction is a number.

38. Compute $\der {} x (e^{3 x} + 1)(\sin 2 x)(x^4 + 2 x + 1)$ .

For a product of three terms, the Product Rule says

$\der {} x (1^{\rm st})(2^{\rm nd})(3^{\rm rd}) = (1^{\rm st})(2^{\rm nd})\left(\der {} x (3^{\rm rd})\right) + (1^{\rm st})\left(\der {} x (2^{\rm nd})\right)(3^{\rm rd}) + \left(\der {} x (1^{\rm st})\right)(2^{\rm nd})(3^{\rm rd}).$

$\der {} x (e^{3 x} + 1)(\sin 2 x)(x^4 + 2 x + 1) = (e^{3 x} + 1)(\sin 2 x)(4 x^3 + 2) + (e^{3 x} + 1)(2\cos 2 x)(x^4 + 2 x + 1) +$

$\hskip0.5 in (3 e^{3 x})(\sin 2 x)(x^4 + 2 x + 1).\quad\halmos$

39. Find $\der {} x \left(\dfrac{\sqrt{x} + \sec x}{3 + 5 x - \cos x}\right)$ .

Note that

$\dfrac{\sqrt{x} + \sec x}{3 + 5 x - \cos x} = \dfrac{x^{1/2} + \sec x}{3 + 5 x - \cos x}.$

Then

$\der {} x \left(\dfrac{x^{1/2} + \sec x}{3 + 5 x - \cos x}\right) = \dfrac{(3 + 5 x - \cos x)\left(\dfrac{1}{2}x^{-1/2} + \sec x \tan x\right)) - (x^{1/2} + \sec x)(5 + \sin x)}{(3 + 5 x - \cos x)^2} =$

$\dfrac{(3 + 5 x - \cos x)\left(\dfrac{1}{2\sqrt{x}} + \sec x \tan x\right) - (\sqrt{x} + \sec x)(5 + \sin x)}{(3 + 5 x - \cos x)^2}.\quad\halmos$

40. Find if $y = \dfrac{(2 - 3 x - x^5)e^{4 x}}{\tan 5 x + 7}$ .

$y' = \dfrac{(\tan 5 x + 7)\left((2 - 3 x - x^5)(4 e^{4 x}) + (e^{4 x})(-3 - 5 x^4)\right) - (2 - 3 x - x^5)e^{4 x}(5)(\sec 5 x)^2}{(\tan 5 x + 7)^2}.$

I applied the Quotient Rule to the original fraction. In taking the derivative of the top, I also needed to apply the Product Rule.

41. Compute $\der {} x \dfrac{1 + \csc (x^2)}{(e^{-7 x} + 3 x)(7 x^6 + x + 1)}$ .

$\der {} x \dfrac{1 + \csc (x^2)}{(e^{-7 x} + 3 x)(7 x^6 + x + 1)} =$

$\dfrac{(e^{-7 x} + 3 x)(7 x^6 + x + 1)(2 x)(-\csc (x^2) \cot (x^2)) - (1 + \csc (x^2)) \left((e^{-7 x} + 3 x)(42 x^5 + 1) + (7 x^6 + x + 1)(-7 e^{-7 x} + 3)\right)}{(e^{-7 x} + 3 x)^2(7 x^6 + x + 1)^2}.$

I applied the Quotient Rule to the original fraction. In taking the derivative of the bottom, I also needed to apply the Product Rule.

42. Compute $\der {} x \left(\dfrac{x^2 + x + 1}{x^3 - 3 x + 5}\right)^{11}$ .

$\der {} x \left(\dfrac{x^2 + x + 1}{x^3 - 3 x + 5}\right)^{11} = 11 \left(\dfrac{x^2 + x + 1}{x^3 - 3 x + 5}\right)^{10} \left(\dfrac{(x^3 - 3 x + 5)(2 x + 1) - (x^2 + x + 1)(3 x^2 - 3)}{(x^3 - 3 x + 5)^2}\right).\quad\halmos$

43. Compute $\der {} x \left(e^{x^2} + 7^{x^2} + e^{7 x} + 7^{e^x}\right)$ .

$\der {} x \left(e^{x^2} + 7^{x^2} + e^{7 x} + 7^{e^x}\right) = 2 x e^{x^2} + 2 x (\ln 7) 7^{x^2} + 7 e^{7 x} + (e^x) (\ln 7) 7^{e^x}.\quad\halmos$

44. Compute $\der {} x \root 3 \of {(x^2 + e^x)(\ln x + 42 x) + x^3}$ .

Note that

$\root 3 \of {(x^2 + e^x)(\ln x + 42 x) + x^3} = \left((x^2 + e^x)(\ln x + 42 x) + x^3\right)^{1/3}.$

Then

$\der {} x \left((x^2 + e^x)(\ln x + 42 x) + x^3\right)^{1/3} =$

$\dfrac{1}{3} \left((x^2 + e^x)(\ln x + 42 x) + x^3\right)^{-2/3} \left((x^2 + e^x)\left(\dfrac{1}{x} + 42\right) + (\ln x + 42 x)(2 x + e^x) + 3 x^2\right).\quad\halmos$

45. Compute $\der {} w \ln \sqrt{e^{w^2} + e^{2 w} + 1}$ .

Note that

$\ln \sqrt{e^{w^2} + e^{2 w} + 1} = \ln \left(e^{w^2} + e^{2 w} + 1\right)^{1/2} = \dfrac{1}{2} \ln \left(e^{w^2} + e^{2 w} + 1\right).$

Then

$\der {} w \left(\dfrac{1}{2} \ln \left(e^{w^2} + e^{2 w} + 1\right)\right) = \dfrac{1}{2} \cdot \dfrac{2 w e^{w^2} + 2 e^{2 w}}{e^{w^2} + e^{2 w} + 1} = \dfrac{w e^{w^2} + e^{2 w}}{e^{w^2} + e^{2 w} + 1}.\quad\halmos$

46. Compute $\der {} x \left(x^3 + \left(x^3 + (x^3 + 1)^3\right)^3\right)^3$ .

$\der {} x \left(x^3 + \left(x^3 + (x^3 + 1)^3\right)^3\right)^3 =$

$3\left(x^3 + \left(x^3 + (x^3 + 1)^3\right)^3\right)^2 \left(3 x^2 + 3 \left(x^3 + (x^3 + 1)^3\right)^2 \left(3 x^2 + 3 (x^3 + 1)^2 (3 x^2)\right)\right).\quad\halmos$

47. Compute $\der {} x \left(\dfrac{2 x + 5}{(x + 2)^3}\right)$ .

$\der {} x \left(\dfrac{2 x + 5}{(x + 2)^3}\right) = \dfrac{(x + 2)^3(2) - (2 x + 5)(3)(x + 2)^2}{(x + 2)^6} = \dfrac{(x + 2)(2) - (2 x + 5)(3)}{(x + 2)^4} =$

$\dfrac{2 x + 4 - 6 x - 15}{(x + 2)^4} = \dfrac{-4 x - 11}{(x + 2)^4}.$

In going from the second expression to the third, I cancelled a common factor of . If you try to multiply before you cancel, you'll get a big mess, and it will be much harder to simplify.

48. Compute the derivative with respect to t of $s(t) = \sec \left(\dfrac{5}{t^3 + 5 t + 8}\right)$ .

Rewrite the function as

$s(t) = \sec \left(5(t^3 + 5 t + 8)^{-1}\right).$

Then

$s'(t) = \left(\sec \left(5(t^3 + 5 t + 8)^{-1}\right) \tan \left(5(t^3 + 5 t + 8)^{-1}\right)\right) \left((5)(-1)(t^3 + 5 t + 8)^{-2}(3 t^2 + 5)\right) =$

$\left(\sec \left(5(t^3 + 5 t + 8)^{-1}\right) \tan \left(5(t^3 + 5 t + 8)^{-1}\right)\right) \left(\dfrac{-5(3 t^2 + 5)}{(t^3 + 5 t + 8)^2}\right).\quad\halmos$

49. Compute $\der {} x [\log_5 (x^2 + x + 1)]^7$ .

$\der {} x [\log_5 (x^2 + x + 1)]^7 = \left(7 [\log_5 (x^2 + x + 1)]^6\right) \left(\dfrac{2 x + 1}{(x^2 + x + 1) \ln 5}\right).\quad\halmos$

50. Compute for .

$y'' = 8\left((x)(3)(x^2 + 1)^2(2 x) + (x^2 + 1)^3\right) = 48 x^2(x^2 + 1)^2 + 8(x^2 + 1)^3,$

$y''' = 48\left((x^2)(2)(x^2 + 1)(2 x) + (x^2 + 1)^2(2 x)\right) + (8)(3)(x^2 + 1)^2(2 x) =$

$\hskip0.5 in 192 x^3(x^2 + 1) + 96 x(x^2 + 1)^2 + 48 x(x^2 + 1)^2 = 192 x^3(x^2 + 1) + 144 x(x^2 + 1)^2.\quad\halmos$

51. Compute $y^{(50)}$ if $y = \dfrac{1}{4 - x}$ .

I'll compute the first few derivatives until I see the pattern.

$y' = \dfrac{1}{(4 - x)^2},$

$y'' = \dfrac{2}{(4 - x)^3},$

$y''' = \dfrac{2\cdot 3}{(4 - x)^4},$

$y^{(4)} = \dfrac{2\cdot 3\cdot 4}{(4 - x)^5}.$

Note that I don't get minus signs here; the powers are negative, but the Chain Rule requires the derivative of , which is -1. The two negatives cancel.

Note also that, in order to see the pattern, I did not multiply out the numbers on the top.

Based on the pattern, I see that the power on the bottom is one more than the order of the derivative. On the top, I get the product of the numbers from 2 through the order of the derivative. So

$y^{(50)} = \dfrac{2 \cdot 3 \cdot \cdots \cdot 50}{(4 - x)^{51}}.$

(You can also write the top as (50-factorial).)

52. Compute $\der {} x \sqrt{e^{f(x)^2} + 1}$ .

Since is not given, the answer will come out in terms of and .

Note that

$\sqrt{e^{f(x)^2} + 1} = \left(e^{f(x)^2} + 1\right)^{1/2}.$

Then

$\der {} x \left(e^{f(x)^2} + 1\right)^{1/2} = \dfrac{1}{2}\left(e^{f(x)^2} + 1\right)^{-1/2} \left(e^{f(x)^2}\right)(2 f(x))(f'(x)).\quad\halmos$

53. Compute $\der {} x \ln(\sin (g(x)) + 1)$ .

Since is not given, the answer will come out in terms of and .

$\der {} x \ln(\sin (g(x)) + 1) = \dfrac{(\cos (g(x))(g'(x))}{\sin (g(x)) + 1}.\quad\halmos$

54. f and g are differentiable functions. The values of f, g, , and at and are shown below:

Compute , $\left(\dfrac{f}{g}\right)'(2)$ , and .

By the Product Rule,

By the Quotient Rule,

$\left(\dfrac{f}{g}\right)'(2) = \dfrac{g(2) f'(2) - f(2) g'(2)}{g(2)^2} = \dfrac{(5)(4) - (-6)(10)}{5^2} = \dfrac{16}{5}.$

By the Chain Rule,

$[f(g)]'(2) = f'(g(2)) \cdot g'(2) = f'(5) \cdot g'(2) = 7 \cdot 10 = 70.\quad\halmos$

55. Find the equation of the tangent line to the graph of at .

When ,

$f(2) = 2^3 + 5 \cdot 2 - 10 = 8.$

The point of tangency is .

I have

$f'(x) = 3 x^2 + 5, \quad\hbox{so}\quad f'(2) = 17.$

The tangent line is

$17 (x - 2) = y - 8, \quad\hbox{or}\quad y = 17 x - 26.\quad\halmos$

56. Find the equation of the tangent line to the graph of $y = \dfrac{1}{(x^2 + 4 x + 5)^2}$ at .

When ,

$y \dfrac{1}{(1 + 4 + 5)^2} = \dfrac{1}{100}.$

The point of tangency is $\left(1, \dfrac{1}{100}\right)$ .

$y = (x^2 + 4 x + 5)^{-2}$ , so

$y' = (-2)(x^2 + 4 x + 5)^{-3}(2 x + 4), \quad\hbox{and}\quad y'(1) = -\dfrac{3}{250}.$

The tangent line is

$-\dfrac{3}{250}(x - 1) = y - \dfrac{1}{100}.\quad\halmos$

57. For what value or values of c does the tangent line to the graph of at pass through the point ?

At , I have . Also,

$y' = 2 x + 5, \quad\hbox{so}\quad y'(c) = 2 c + 5.$

The tangent line to at is

I want this line to pass through the point , so plug the point into the line equation and solve for c:

$\eqalign{ 6 - (c^2 + 5 c + 1) & = (2 c + 5)(1 - c) \cr -c^2 - 5 c + 5 & = -2 c^2 - 3 c + 5 \cr c^2 - 2 c & = 0 \cr c(c - 2) & = 0 \cr}$

The values of c are and .

58. The position of a cheeseburger at time t is given by

Find the value(s) of t for which the velocity is 0. Find the value(s) of t for which the acceleration is 0.

The velocity is the derivative of the position:

I have for and .

The acceleration is derivative of the velocity (or the second derivative of the position):

(Note: I differentiated , not . Differentiating the first expression is easier than differentiating the second.)

I have for .

59. For what values of x is the function $f(x) = \dfrac{x - 5}{x^2 - 3 x - 10}$ continuous?

The function will be continuous where it's defined, so I have to find the domain.

$f(x) = \dfrac{x - 5}{(x - 5)(x + 2)}.$

I can't divide by 0, and division by 0 occurs when or .

(You can't cancel the 's, because that assumes $x - 5 \ne 0$ .)

Thus, the domain is $x \ne -2, 5$ , and that is where f is continuous.

60. For what values of x is the function $f(x) = \dfrac{1}{\sqrt{x^2 + 5 x + 6}}$ continuous?

The function will be continuous where it's defined, so I have to find the domain.

$f(x) = \dfrac{1}{\sqrt{(x + 2)(x + 3)}}.$

I can't divide by 0, and division by 0 occurs where $\sqrt{(x + 2)(x + 3)} = 0$ . Square both sides: . I get or .

I can't take the square root of a negative number, and this occurs where .

You can solve the inequality by constructing a sign chart.

Alternatively, graph the quadratic. is a parabola opening upward (since it's , which has a positive -term). It has roots at and at . Picture:

$\hbox{\epsfysize=2 in \epsffile{rev1-3.eps}}$

From the graph, you can see that for .

I throw out the bad points , , . The domain is or , and that is where f is continuous.

61. Let

$f(x) = \cases{ \dfrac{x^2 - 7 x - 8}{x + 1} & if $x \ne -1$ \cr \noalign{\vskip2pt} 9& if $x = -1$ \cr}$

Prove or disprove: f is continuous at .

$\lim_{x \to -1} f(x) = \lim_{x \to -1} \dfrac{x^2 - 7 x - 8}{x + 1} = \lim_{x \to -1} \dfrac{(x - 8)(x + 1)}{x + 1} = \lim_{x \to -1} (x - 8) = -9.$

On the other hand, . Since $\displaystyle \lim_{x \to -1} f(x) \ne f(-1)$ , f is not continuous at .

62. Find the value of c which makes the following function continuous at :

$f(x) = \cases{ 1 + 3 x - c x^2 & if $x < 2$ \cr 7 x + 3 & if $x \ge 2$ \cr}.$

For f to be continuous at , $\displaystyle \lim_{x \to 2} f(x)$ must be defined. This will happen if the left and right-hand limits at are equal. Compute the limits:

$\lim_{x \to 2^+} f(x) = \lim_{x \to 2^+} (7 x + 3) = 17,$

$\lim_{x \to 2^-} f(x) = \lim_{x \to 2^-} (1 + 3 x - c x^2) = 7 - 4 c.$

Set the left and right-hand limits equal and solve for c:

$7 - 4 c = 17, \quad -4 c = 10, \quad c = -\dfrac{5}{2}.$

This value of c will make the left and right-hand limits equal to 17, so in this case, $\displaystyle \lim_{x \to 2} f(x) = 17$ . Since , it follows that $\displaystyle \lim_{x \to 2} f(x) = f(2)$ , and f is continuous at .

63. Prove that has a root between and .

f is continuous, since it's a polynomial.

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & x & & $f(x) = x^5 + 4 x + 1$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & -1 & & -4 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 0 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }}$

Since f is negative when and f is positive when , the Intermediate Value Theorem implies that for some number c between -1 and 0.

64. Suppose f is continuous, , and . Prove that there is a number x between 2 and 5 such that $x^3 \cdot f(x) = 110$ .

and are continuous, so $x^3 \cdot f(x)$ is continuous.

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & x & & $x^3 \cdot f(x)$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 2 & & $8 \cdot 13 = 104$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 5 & & $125 \cdot 1 = 125$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }}$

Since is continuous, and since 110 is between 104 and 125, the Intermediate Value Theorem says that there is a number x between 2 and 5 such that $x^3\cdot f(x) = 110$ .

65. Suppose $f(x) = \sqrt{x - 6}$ . Use the limit definition of the derivative to compute .

$f'(15) = \lim_{h\to 0} \dfrac{f(15 + h) - f(15)}{h}.$

Now

$f(15) = \sqrt{15 - 6} = \sqrt{9} = 3,$

$f(15 + h) = \sqrt{(15 + h) - 6} = \sqrt{9 + h}.$

$f'(15) = \lim_{h\to 0} \dfrac{\sqrt{9 + h} - 3}{h} = \lim_{h\to 0} \dfrac{\sqrt{9 + h} - 3}{h} \cdot \dfrac{\sqrt{9 + h} + 3}{\sqrt{9 + h} + 3} =$

$\lim_{h\to 0} \dfrac{(\sqrt{9 + h})^2 - 3^2}{h(\sqrt{9 + h} + 3)} = \lim_{h\to 0} \dfrac{(9 + h) - 9}{h(\sqrt{9 + h} + 3)} = \lim_{h\to 0} \dfrac{h}{h(\sqrt{9 + h} + 3)} = \lim_{h\to 0} \dfrac{1}{\sqrt{9 + h} + 3} = \dfrac{1}{6}.\quad\halmos$

66. Suppose $f(x) = \dfrac{1}{x + 3}$ . Use the limit definition of the derivative to compute .

I'll simplify the quotient $\dfrac{f(x + h) - f(x)}{h}$ , then plug it into the limit.

$f(x + h) - f(x) = \dfrac{1}{x + h + 3} - \dfrac{1}{x + 3} = \dfrac{(x + 3) - (x + h + 3)}{(x + h + 3)(x + 3)} = \dfrac{-h}{(x + h + 3)(x + 3)}.$

Therefore,

$\dfrac{f(x + h) - f(x)}{h} = \dfrac{\dfrac{-h}{(x + h + 3)(x + 3)}}{h} = \dfrac{-h}{h(x + h + 3)(x + 3)} = \dfrac{-1}{(x + h + 3)(x + 3)}.$

Hence,

$f'(x) = \lim_{h\to 0} \dfrac{f(x + h) - f(x)}{h} = \lim_{h\to 0} \dfrac{-1}{(x + h + 3)(x + 3)} = -\dfrac{1}{(x + 3)^2}.\quad\halmos$

67. Suppose $f(x) = \dfrac{1}{\sqrt{x} + 1}$ . Use the limit definition of the derivative to compute .

$f'(x) = \lim_{h\to 0} \dfrac{f(x + h) - f(x)}{h} = \lim_{h\to 0} \dfrac{\dfrac{1}{\sqrt{x + h} + 1} - \dfrac{1}{\sqrt{x} + 1}}{h} =$

$\lim_{h\to 0} \dfrac{\dfrac{1}{\sqrt{x + h} + 1} - \dfrac{1}{\sqrt{x} + 1}}{h}\cdot \dfrac{(\sqrt{x} + 1)(\sqrt{x + h} + 1)} {(\sqrt{x} + 1)(\sqrt{x + h} + 1)} = \lim_{h\to 0} \dfrac{(\sqrt{x} + 1) - (\sqrt{x + h} + 1)} {h(\sqrt{x} + 1)(\sqrt{x + h} + 1)} =$

$\lim_{h\to 0} \dfrac{\sqrt{x} - \sqrt{x + h}} {h(\sqrt{x} + 1)(\sqrt{x + h} + 1)} = \lim_{h\to 0} \dfrac{\sqrt{x} - \sqrt{x + h}} {h(\sqrt{x} + 1)(\sqrt{x + h} + 1)}\cdot \dfrac{\sqrt{x} + \sqrt{x + h}}{\sqrt{x} + \sqrt{x + h}} =$

$\lim_{h\to 0} \dfrac{x - (x + h)} {h(\sqrt{x} + 1)(\sqrt{x + h} + 1)(\sqrt{x} + \sqrt{x + h})} = \lim_{h\to 0} \dfrac{-h} {h(\sqrt{x} + 1)(\sqrt{x + h} + 1)(\sqrt{x} + \sqrt{x + h})} =$

$\lim_{h\to 0} \dfrac{-1} {(\sqrt{x} + 1)(\sqrt{x + h} + 1)(\sqrt{x} + \sqrt{x + h})} = \dfrac{-1}{2(\sqrt{x} + 1)^2\sqrt{x}}.\quad\halmos$

68. The graph of a function is pictured below. For what values of x is f continuous but not differentiable? For what values of f is f not continuous?

$\hbox{\epsfysize=2.5 in \epsffile{rev1-1.eps}}$

f is continuous but not differentiable at and at , since at those points the graph is unbroken but has corners.

f is not continuous at and at .

69. (a) Find the average rate of change of on the interval $1 \le x \le 3$ .

(b) Find the instantaneous rate of change of at .

(a)

$\dfrac{f(3) - f(1)}{3 - 1} = \dfrac{14 - 0}{3 - 1} = 7.\quad\halmos$

(b)

$f'(x) = 2 x + 3, \quad\hbox{so}\quad f'(3) = 6 + 3 = 9.\quad\halmos$

70. Give an example of a function which is defined for all x and a number c such that

$\lim_{x \to c} f(x) \ne f(c).$

There are lots of possible answers to this question. For example, let

$f(x) = \cases{ x & if $x \ne 0$ \cr 1 & if $x = 0$ \cr}$

Then

$\lim_{x \to 0} f(x) = \lim_{x \to 0} x = 0, \quad\hbox{but}\quad f(0) = 1.$

Of course, the condition $\lim_{x \to c} f(x) \ne f(c)$ means that the function is not continuous at c. The value of $\lim_{x \to c} f(x)$ (or even its existence) does not depend on the value of (or even its existence).

71. Suppose $f(x) = \dfrac{x + 1}{x + 2}$ . Find $f^{-1}(x)$ .

Let $y = \dfrac{x + 1}{x + 2}$ . Swap x's and y's and solve for y:

$\eqalign{ x & = \dfrac{y + 1}{y + 2} \cr (y + 2) \cdot x & = (y + 2) \cdot \dfrac{y + 1}{y + 2} \cr x(y + 2) & = y + 1 \cr xy + 2 x & = y + 1 \cr xy + 2 x - 2 x - y & = y + 1 - 2 x - y \cr xy - y & = 1 - 2 x \cr y(x - 1) & = 1 - 2 x \cr \dfrac{1}{x - 1} \cdot y(x - 1) & = \dfrac{1}{x - 1} \cdot (1 - 2 x) \cr y & = \dfrac{1 - 2 x}{x - 1} \cr}$

Therefore, $f^{-1}(x) = \dfrac{1 - 2 x}{x - 1}$ .

72. Suppose and . Find $(f^{-1})'(5)$ .

First, notice that means $f^{-1}(5) = 2$ . I'll use the formula

$(f^{-1})'(x) = \dfrac{1}{f'(f^{-1}(x))}.$

Setting , I get

$(f^{-1})'(5) = \dfrac{1}{f'(f^{-1}(5))} = \dfrac{1}{f'(2)} = \dfrac{1}{7}.\quad\halmos$

73. Suppose and $f'(x) = \sqrt{x^4 + x^2 + 16}$ . Find $(f^{-1})'(5)$ .

First, notice that means $f^{-1}(5) = 2$ . I'll use the formula

$(f^{-1})'(x) = \dfrac{1}{f'(f^{-1}(x))}.$

Setting , I get

$(f^{-1})'(5) = \dfrac{1}{f'(f^{-1}(5))} = \dfrac{1}{f'(2)} = \dfrac{1}{\sqrt{2^4 + 2^2 + 16}} = \dfrac{1}{6}.\quad\halmos$

74. Suppose $f(x) = (x^5 + 2 x^3 + 5)^{1/3}$ . Find $(f^{-1})'(2)$ .

It looks like I need in this problem, so I'll do that first. By the Chain Rule,

$f'(x) = \dfrac{1}{3}(x^5 + 2 x^3 + 5)^{-2/3}(5 x^4 + 6 x^2).$

I'll use the formula

$(f^{-1})'(x) = \dfrac{1}{f'(f^{-1}(x))}.$

Setting , I get

$(f^{-1})'(2) = \dfrac{1}{f'(f^{-1}(2))}. \eqno{(*)}$

I need to find $f^{-1}(2)$ . Remember that

$f^{-1}(2) = A \quad\hbox{means}\quad f(A) = 2.$

So I want to find a number A such that , or

$(A^5 + 2 A^3 + 5)^{1/3} = 2.$

If you try to solve this algebraically for A, you might get as far as

$\eqalign{ (A^5 + 2 A^3 + 5)^{1/3} & = 2 \cr [(A^5 + 2 A^3 + 5)^{1/3}]^3= 2^3 \cr A^5 + 2 A^3 + 5 & = 8 \cr A^5 + 2 A^3 - 3 & = 0 \cr}$

But you probably don't know any method or formula for solving this kind of equation.

However, the problem was intended to be doable, so if you can't solve systematically, it must be intended that you should use trial and error. And if it's trial and error, the answer is probably not something like " ". So try a few small numbers for A --- plug them into and see if you can find one that works.

If you do this, you find that solves the equation. Thus, , so $f^{-1}(2) = 1$ . Now going back to (*), I get

$(f^{-1})'(2) = \dfrac{1}{f'(f^{-1}(2))} = \dfrac{1}{f'(1)} = \dfrac{1}{\left(\dfrac{1}{3} \cdot (8^{-2/3}) \cdot 11\right)} = \dfrac{1}{\left(\dfrac{11}{12}\right)} = \dfrac{12}{11}.\quad\halmos$

75. Compute $\der {} x (x^2 + 3 x + 1)^{(x^2+6)}$ .

Let $y = (x^2 + 3 x + 1)^{(x^2+6)}$ . Take the log of both sides, then differentiate:

$\eqalign{ \ln y & = \ln (x^2 + 3 x + 1)^{(x^2+6)} \cr \ln y & = (x^2 + 6) \ln (x^2 + 3 x + 1) \cr \noalign{\vskip2 pt} \dfrac{y'}{y} & = (x^2 + 6)\left(\dfrac{2 x + 3}{x^2 + 3 x + 1}\right) + [\ln (x^2 + 3 x + 1)](2 x) \cr \noalign{\vskip2 pt} y' & = y\left[(x^2 + 6)\left(\dfrac{2 x + 3}{x^2 + 3 x + 1}\right) + 2 x \ln (x^2 + 3 x + 1) \right] \cr y' & = (x^2 + 3 x + 1)^{(x^2+6)} \left[(x^2 + 6)\left(\dfrac{2 x + 3}{x^2 + 3 x + 1}\right) + 2 x \ln (x^2 + 3 x + 1) \right] \cr}$

Note that in the next-to-the-last step, I changed $[\ln (x^2 + 3 x + 1)](2 x)$ to $2 x \ln (x^2 + 3 x + 1)$ . If you don't do this, you must have the $[\cdot]$ 's around $\ln (x^2 + 3 x + 1)$ . Writing " $\ln (x^2 + 3 x + 1)(2 x)$ " is not correct.

76. Compute $\der {} x (e^x + 1)^{\sin x}$ .

Let $y = (e^x + 1)^{\sin x}$ . Take the log of both sides, then differentiate:

$\eqalign{ \ln y & = \ln (e^x + 1)^{\sin x} \cr \ln y & = (\sin x) \ln (e^x + 1) \cr \noalign{\vskip2 pt} \dfrac{y'}{y} & = (\sin x)\left(\dfrac{e^x}{e^x + 1}\right) + [\ln (e^x + 1)](\cos x) \cr \noalign{\vskip2 pt} y' & = y\left((\sin x)\left(\dfrac{e^x}{e^x + 1}\right) + [\ln (e^x + 1)](\cos x)\right) \cr \noalign{\vskip2 pt} y' & = (e^x + 1)^{\sin x} \left((\sin x)\left(\dfrac{e^x}{e^x + 1}\right) + [\ln (e^x + 1)](\cos x)\right) \quad\halmos \cr}$

77. Find the equation of the tangent line to at .

When , I have , so the point of tangency is .

Use logarithmic differentiation to find :

$\eqalign{ y & = (x^2 + 2)^x \cr \ln y & = \ln (x^2 + 2)^x \cr \ln y & = x \ln (x^2 + 2) \cr \noalign{\vskip2 pt} \dfrac{y'}{y} & = x\left(\dfrac{2 x}{x^2 + 2}\right) + \ln (x^2 + 2) \cr \noalign{\vskip2 pt} y' & = y\left[x\left(\dfrac{2 x}{x^2 + 2}\right) + \ln (x^2 + 2)\right] \cr y' & = (x^2 + 2)^x \cdot \left[x\left(\dfrac{2 x}{x^2 + 2}\right) + \ln (x^2 + 2)\right] \cr}$

Plug in :

$y' = 3 \cdot \left(1 \cdot \dfrac{2}{3} + \ln 3\right) = 2 + 3 \ln 3.$

The line is

$y - 3 = (2 + 3 \ln 3)(x - 1).\quad\halmos$

78. (An alternate approach to logarithmic differentiation)

(a) Use the identity $A = e^{\ln A}$ to write $(x^2 + 1)^{\tan x}$ using $e^{(\cdot)}$ and $\ln {(\cdot)}$ .

(b) Use the Chain Rule to differentiate the expression you obtained in (a). (This gives another way of doing logarithmic differentiation involving powers.)

(a)

$(x^2 + 1)^{\tan x} = e^{\ln (x^2 + 1)^{\tan x}} = e^{(\tan x) \ln (x^2 + 1)}.\quad\halmos$

(b) I'll differentiate $e^{(\tan x) \ln (x^2 + 1)}$ using the Chain Rule. The outer function is the exponential $e^{(\cdot)}$ ; to differentiate the inner function $(\tan x) \ln (x^2 + 1)$ , I'll use the Product Rule.

$\der {} x e^{(\tan x) \ln (x^2 + 1)} = \left(e^{(\tan x) \ln (x^2 + 1)}\right) \left[(\tan x)\left(\dfrac{2 x}{x^2 + 1}\right) + \left(\ln (x^2 + 1)\right)\left((\sec x)^2\right)\right] =$

$(x^2 + 1)^{\tan x} \left[(\tan x)\left(\dfrac{2 x}{x^2 + 1}\right) + \left(\ln (x^2 + 1)\right)\left((\sec x)^2\right)\right].$

In other words,

$\der {} x (x^2 + 1)^{\tan x} = (x^2 + 1)^{\tan x} \left[(\tan x)\left(\dfrac{2 x}{x^2 + 1}\right) + \left(\ln (x^2 + 1)\right)\left((\sec x)^2\right)\right]. \quad\halmos$

79. Find if y is defined implicitly by

$\sin x + \cos y = 3 x + 5 y.$

Differentiate implicitly and solve for y:

$\eqalign{ \cos x + (-\sin y) y' & = 3 + 5 y' \cr (-\sin y) y' - 5 y' & = 3 - \cos x \cr y' (-\sin y - 5) & = 3 - \cos x \cr \noalign{\vskip2 pt} y' & = \dfrac{3 - \cos x}{-\sin y - 5} = \dfrac{\cos x - 3}{\sin y + 5} \quad\halmos \cr}$

80. Find the equation of the tangent line to the curve

$x^3 + 2 x y^3 = x^2 - y^2 + 3 \quad\hbox{at the point}\quad (1,1).$

Differentiate implicitly:

Note: If you have a point to plug in, plug the point in before you solve for .

Plug in , :

$3 + 2 + 6 y' = 2 - 2 y', \quad y' = -\dfrac{3}{8}.$

The tangent line is

$-\dfrac{3}{8} (x - 1) = y - 1.\quad\halmos$

81. Find the equation of the tangent line to the curve

$\dfrac{x^2}{y} + y^2 = 7 x - 2 y - 9 \quad\hbox{at the point}\quad (3, 1).$

Differentiate implicitly:

$\dfrac{y \cdot 2 x - x^2 y'}{y^2} + 2 y y' = 7 - 2 y'.$

Note: If you have a point to plug in, plug the point in before you solve for .

Plug in , :

$(6 - 9 y') + 2 y' = 7 - 2 y', \quad -5 y' = 1, \quad y' = -\dfrac{1}{5}.$

The tangent line is

$y - 1 = -\dfrac{1}{5} (x - 3).\quad\halmos$

82. Find at the point on the curve

Differentiate implicitly:

$x^3 y' + 3 x^2 y + 4 x = 3 y^2 y' - 2 y'. \eqno{(*)}$

Plug in and and solve for :

$y' + 6 + 4 = 12 y' - 2 y', \quad y' = \dfrac{10}{9}.$

Differentiate (*) implicitly:

Plug in , , and $y' = \dfrac{10}{9}$ and solve for :

$y'' + 3\left(\dfrac{10}{9}\right) + 3\left(\dfrac{10}{9}\right) + 12 + 4 = 12 y'' + 12\left(\dfrac{10}{9}\right)^2 - 2 y'', \quad y'' = \dfrac{212}{243}.\quad\halmos$

He who climbs onto the roof should not push away the ladder. - Karol Irzykowski

Contact information

Bruce Ikenaga's Home Page