Review Problems for Test 2

Math 161

These problems are provided to help you study. The fact that a problem occurs here does not mean that there will be a similar problem on the test. And the absence of a problem from this review sheet does not mean that there won't be a problem of that kind on the test.

Many applications of differentiation (such as finding absolute maxima and minima and graphing curves) require you to find derivatives and simplify them. The first set of problems will help you review your differentiation skills.

1. Compute the derivatives of the following functions, simplifying your answers.

(a) $f(x) = -\dfrac{1}{x} + \dfrac{1}{x^2} + \dfrac{8}{3 x^3}$ .

(b) $g(x) = (x^2 - 7 x + 13) e^x$ .

(c) $y = \dfrac{6}{5} x^5 + \dfrac{9}{2} x^4 - 8 x^3 + 3$ .

(d) $y = \ln x + \dfrac{1}{2 x^2}$ .

(e) $f(x) = \dfrac{3}{4} x^{4/3} - 3 x^{1/3} + \dfrac{9}{x^{2/3}}$ .

In the graphing problems that follow, you should find:

(a) The domain of the function.

(b) The x and y-intercepts (if any). In some cases, you may need to estimate the values numerically.

(c) The derivatives $f'(x)$ and $f''(x)$ , if they aren't given.

(d) The intervals on which the function increases, and the intervals n which it decreases.

(e) The x-coordinates of any local maxima or minima.

(f) The intervals on which the function is concave up, and the intervals n which it is concave down.

(g) The x-coordinates of any inflection points.

(h) Any horizontal asymptotes.

(i) Any vertical asymptotes.

(j) A qualitatively accurate sketch of the graph.

2. Graph $y = 2 x^{3/2} - 6 x^{1/2}$ .

3. Graph $y = \dfrac{x}{\sqrt{x^2 + 7}}$ .

4. Graph $y = 5 x^{2/5} + \dfrac{5}{7} x^{7/5}$ .

5. Graph $y = \dfrac{2 x}{x^2 - 1}$ .

6. Graph $f(x) = (x^2 - 4 x + 5) e^x$ .

7. Graph $f(x) = (x - 2)(x - 3) + 2 \ln x$ .

8. Graph $f(x) = \dfrac{1}{6} \dfrac{x - 1}{(x + 1)^3}$ .

Hint: The derivatives are

$$f'(x) = -\dfrac{1}{3} \dfrac{x - 2}{(x + 1)^4} \quad\hbox{and}\quad f''(x) = \dfrac{x - 3}{(x + 1)^5}.$$

9. A function $y = f(x)$ is defined for all x. In addition:

$$f(-1) = 0 \quad\hbox{and}\quad f'(3) \quad\hbox{is undefined},$$

$$f'(x) \ge 0 \quad\hbox{for}\quad x \le 2 \quad\hbox{and}\quad x > 3,$$

$$f'(x) \le 0 \quad\hbox{for}\quad 2 \le x < 3,$$

$$f''(x) < 0 \quad\hbox{for}\quad x < 3,$$

$$f''(x) > 0 \quad\hbox{for}\quad x > 3.$$

Sketch the graph of f.

10. Sketch the graph of $y = |x^2 - 6 x + 5|$ by first sketching the graph of $y = x^2 - 6 x + 5$ .

11. Find the critical points of $y = \dfrac{1}{3}x^3 + \dfrac{3}{2}x^2 - 4 x + 5$ and classify them as local maxima or local minima using the Second Derivative Test.

12. Find the critical points of $y = -\dfrac{1}{x} + \dfrac{4}{x^2} - \dfrac{4}{x^3}$ and classify them as local maxima or local minima using the Second Derivative Test.

13. For $f(x) = \dfrac{6}{x + 1}$ , use differentials to approximate $f(2.04)$ .

14. Suppose $y = f(x)$ is a differentiable function, $f(3) = 4$ , and $f'(3) = -6$ . Use differentials to approximate $f(3.01)$ .

15. The derivative of a function $y = f(x)$ is $y' = \dfrac{1}{x^4 + x^2 + 2}$ . Approximate the change in the function as x goes from 1 to 0.99.

16. Use a linear approximation to approximate $\sqrt{1.99^3 + 1}$ to five decimal places.

17. The area of a sphere of radius r is $A = 4 \pi r^2$ . Suppose that the radius of a sphere is measured to be 5 meters with an error of $\pm 0.2$ meters. Use a linear approximation to approximate the error in the area and the percentage error.

18. x and y are related by the equation

$$\dfrac{x^3}{y} - 4 y^2 = 6 xy - 8 y.$$

Find the rate at which x is changing when $x = 2$ and $y = 1$ , if y decreases at 21 units per second.

19. The volume of a cylinder of radius r and height h is $V = \pi r^2 h$ . Find the rate at which the volume is changing when the radius is 6 and the height is 4, if the radius increases at 2 units per second and the height decreases at 3 units per second.

20. Let x and y be the two legs of a right triangle. Suppose the area is decreasing at 3 square units per second, and x is increasing at 5 units per second. Find the rate at which y is changing when $x = 6$ and $y = 20$ .

21. A bagel (with lox and cream cheese) moves along the curve $y = x^2 + 1$ in such a way that its x-coordinate increases at 3 units per second. At what rate is its y-coordinate changing when it's at the point $(2,5)$ ?

22. Bonzo ties Calvin to a large helium balloon, which floats away at a constant altitude of 600 feet. Bonzo pays out the rope attached to the balloon at 3 feet per second. How rapidly is the balloon moving horizontally at the instant when 1000 feet of rope have been let out? (Assume that the rope remains taut.)

23. Bonzo ties Calvin to a large helium balloon, which floats away at a constant altitude of 600 feet. Bonzo pays out the rope attached to the balloon at 3 feet per second. How rapidly is the angle between the rope and the ground changing at the instant when 1000 feet of rope have been let out? (Assume that the rope remains taut.)

24. A poster 6 feet high is mounted on a wall, with the bottom edge 5 feet above the ground. Calvin walks toward the picture at a constant rate of 2 feet per week. His eyes are level with the bottom edge of the picture. Let $\theta$ be the vertical angle subtended by the picture at Calvin's eyes. At what rate is $\theta$ changing when Calvin is 8 feet from the picture?

25. Find the number(s) c satisfying the conclusion of the Mean Value Theorem for $f(x) = x^3 + 3 x + 5$ on the interval $1 \le x \le 3$ .

26. Prove that the equation $x^5 + 7 x^3 + 13 x - 5 = 0$ has exactly one root.

27. Suppose that f is a differentiable function, $f(3) = 10$ and $f'(x) > 7$ for all x. Prove that $f(5) > 24$ .

28. Suppose that f is a differentiable function, $f(4) = 7$ and $|f'(x)| \le 10$ for all x. Prove that $-13 \le f(6) \le 27$ .

29. Use the Mean Value Theorem to show that if $0 < x < 1$ , then

$$x + 1 < e^x < e x + 1.$$

30. Show graphically the result of performing two iterations of Newton's method on the function whose graph is shown below.

31. A differentiable function satisfies $f(3) = 0.2$ and $f'(3) = 10$ . If Newton's method is applied to f starting at $x = 3$ , what is the next value of x?

32. Newton's method is applied at a point c, with

$$f(c) = 21 \quad\hbox{and}\quad f'(c) = 35.$$

The new x-value is 1.4. Find c.

33. Use Newton's method to approximate a solution to $x^2 + 2 x = \dfrac{5}{x}$ . Do 5 iterations starting at $x = 1$ , and do your computations to at least 5-place accuracy.

34. Find the absolute max and absolute min of $y = x^3 - 12 x + 5$ on the interval $-1 \le x \le 4$ .

35. Find the absolute max and absolute min of $y = 3 x^{2/3}\left(\dfrac{1}{8}x^2 - \dfrac{1}{5}x - 1\right)$ on the interval $-2 \le x \le 8$ .

36. Find the absolute max and absolute min of $y = \dfrac{2}{x^2} - \dfrac{4}{x^4}$ on the interval $1 \le x \le 3$ .

37. Silas Hogwinder is finding the absolute max and min of $f(x) = x^3 - 3 x + 2$ on the interval $-3 \le x \le 3$ . Silas constructs the following sign chart for $y'$ :

$$\hbox{\epsfxsize=3 in \epsffile{rev2-18.eps}}$$

He concludes that the max is at $x = -1$ and the min is at $x = 1$ . What is wrong with his reasoning?

Solutions to the Review Problems for Test 2

1. Compute the derivatives of the following functions, simplifying your answers.

(a) $f(x) = -\dfrac{1}{x} + \dfrac{1}{x^2} + \dfrac{8}{3 x^3}$ .

(b) $g(x) = (x^2 - 7 x + 13) e^x$ .

(c) $y = \dfrac{6}{5} x^5 + \dfrac{9}{2} x^4 - 8 x^3 + 3$ .

(d) $y = \ln x + \dfrac{1}{2 x^2}$ .

(e) $f(x) = \dfrac{3}{4} x^{4/3} - 3 x^{1/3} + \dfrac{9}{x^{2/3}}$ .

(a) First, write the function using negative powers: It will reduce your chances of making a mistake when you use the power rule:

$$f(x) = -x^{-1} + x^{-2} + \dfrac{8}{3} x^{-3}.$$

Differentiate and simplify:

$$\matrix{ f'(x) & = & x^{-2} - 2 x^{-3} - 8 x^{-4} & \cr \noalign{\vskip2pt} & = & \dfrac{1}{x^2} - \dfrac{2}{x^3} - \dfrac{8}{x^4} & \hbox{(Turn negative powers into fractions)} \cr \noalign{\vskip2pt} & = & \dfrac{1}{x^2} \cdot \dfrac{x^2}{x^2} - \dfrac{2}{x^3} \cdot \dfrac{x}{x} - \dfrac{8}{x^4} & \hbox{(Make a common denominator)} \cr \noalign{\vskip2pt} & = & \dfrac{x^2}{x^4} - \dfrac{2 x}{x^4} - \dfrac{8}{x^4} & \cr \noalign{\vskip2pt} & = & \dfrac{x^2 - 2 x - 8}{x^4} & \hbox{(Combine terms)} \cr \noalign{\vskip2pt} & = & \dfrac{(x - 4)(x + 2)}{x^4} & \hbox{(Factor the top)} \quad\halmos \cr}$$

(b)

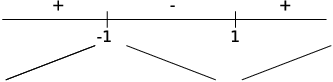
$$\matrix{ g'(x) & = & (x^2 - 7 x + 13) e^x + (e^x)(2 x - 7) & \hbox{(Product Rule)} \cr & = & [(x^2 - 7 x + 13) + (2 x - 7)] e^x & \hbox{(Factor out $e^x$)} \cr & = & (x^2 - 5 x + 6) e^x & \cr & = & (x - 2)(x - 3)) e^x & \quad\halmos \cr}$$

(c)

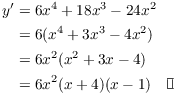
$$\eqalign{ y' & = 6 x^4 + 18 x^3 - 24 x^2 \cr & = 6 (x^4 + 3 x^3 - 4 x^2) \cr & = 6 x^2 (x^2 + 3 x - 4) \cr & = 6 x^2 (x + 4)(x - 1) \quad\halmos \cr}$$

(d) First, write the function using negative powers:

$$y = \ln x + \dfrac{1}{2} x^{-2}.$$

Differentiate:

$$\matrix{ y' & = & \dfrac{1}{x} - x^{-3} & \cr \noalign{\vskip2pt} & = & \dfrac{1}{x} - \dfrac{1}{x^3} & \hbox{(Turn negative powers into fractions)} \cr \noalign{\vskip2pt} & = & \dfrac{1}{x} \cdot \dfrac{x^2}{x^2} - \dfrac{1}{x^3} & \hbox{(Make a common denominator)} \cr \noalign{\vskip2pt} & = & \dfrac{x^2}{x^3} - \dfrac{1}{x^3} & \cr \noalign{\vskip2pt} & = & \dfrac{x^2 - 1}{x^3} & \hbox{(Combine terms)} \cr \noalign{\vskip2pt} & = & \dfrac{(x - 1)(x + 1)}{x^3} & \hbox{(Factor the top)} \quad\halmos\cr}$$

(e) First, write the function using negative powers:

$$f(x) = \dfrac{3}{4} x^{4/3} - 3 x^{1/3} + 9 x^{-2/3}.$$

Differentiate:

$$\matrix{ f'(x) & = & x^{1/3} - x^{-2/3} - 6 x^{-5/3} & \cr & = & x^{1/3} - \dfrac{1}{x^{2/3}} - \dfrac{6}{x^{5/3}} & \hbox{(Turn negative powers into fractions)} \cr \noalign{\vskip2pt} & = & x^{1/3} \cdot \dfrac{x^{5/3}}{x^{5/3}} - \dfrac{1}{x^{2/3}} \cdot \dfrac{x}{x} - \dfrac{6}{x^{5/3}} & \hbox{(Make a common denominator)} \cr \noalign{\vskip2pt} & = & \dfrac{x^2}{x^{5/3}} - \dfrac{x}{x^{5/3}} - \dfrac{6}{x^{5/3}} & \cr \noalign{\vskip2pt} & = & \dfrac{x^2 - x - 6}{x^{5/3}} & \hbox{(Combine terms)} \cr \noalign{\vskip2pt} & = & \dfrac{(x - 3)(x + 2)}{x^{5/3}} & \hbox{(Factor the top)} \quad\halmos \cr}$$

2. Graph $y = 2 x^{3/2} - 6 x^{1/2}$ .

The domain is $x \ge 0$ .

$0 = y = 2 x^{3/2} - 6 x^{1/2} = 2 x^{1/2}(x - 3)$ gives the x-intercepts $x = 0$ and $x = 3$ .

Set $x = 0$ ; the y-intercept is $y = 0$ .

The derivatives are

$$y' = 3 x^{1/2} - 3 x^{-1/2} = \dfrac{3(x - 1)}{x^{1/2}}, \quad y'' = \dfrac{3}{2} x^{-1/2} + \dfrac{3}{2} x^{-3/2} = \dfrac{3}{2}\cdot \dfrac{x + 1}{x^{3/2}}.$$

$y' = \dfrac{3(x - 1)}{x^{1/2}} = 0$ for $x = 1$ ; $y'$ is undefined for $x \le 0$ . ($y = 0$ is an endpoint of the domain.)

$$\hbox{\epsfxsize=3in \epsffile{rev2-1i.eps}}$$

The graph decreases for $0 \le x \le 1$ and increases for $x \ge 1$ .

There is a local (endpoint) max at $(0, 0)$ and a local (absolute) min at $(1, -4)$ .

$y'' = \dfrac{3}{2}\cdot \dfrac{x + 1}{x^{3/2}}$ is always positive, since the factors $\dfrac{3}{2}$ , $x + 1$ , and $x^{3/2}$ are always positive. (Remember that the domain is $x \ge 0$ !) Hence, the graph is always concave up, and there are no inflection points.

There are no vertical asymptotes. The domain ends at $x = 0$ , but $f(0) = 0$ .

Note that

$$\lim_{x \to +\infty} (2 x^{3/2} - 6 x^{1/2}) = +\infty.$$

Therefore, the graph rises on the far right. (It does not make sense to compute $\lim_{x \to -\infty} (2 x^{3/2} - 6 x^{1/2})$ . Why?) Hence, there are no horizontal asymptotes.

$$\hbox{\epsfysize=2in \epsffile{rev2-1g.eps}}\quad\halmos$$

3. Graph $y = \dfrac{x}{\sqrt{x^2 + 7}}$ .

The function is defined for all x.

The x-intercept is $x = 0$ ; the y-intercept is $y = 0$ .

The derivatives are

$$y' = \dfrac{\sqrt{x^2 + 7} - \dfrac{x^2}{\sqrt{x^2 + 7}}}{x^2 + 7} = \dfrac{7}{(x^2 + 7)^{3/2}}, \quad y'' = \dfrac{-21 x}{(x^2 + 7)^{5/2}}.$$

Since $(x^2 + 7)^{3/2} > 0$ for all x, $y'$ is always positive. Hence, the graph is always increasing. There are no maxima or minima.

$y'' = \dfrac{-21 x}{(x^2 + 7)^{5/2}} = 0$ for $x = 0$ ; $y''$ is defined for all x.

$$\hbox{\epsfxsize=3in \epsffile{rev2-2c.eps}}$$

The graph is concave up for $x < 0$ and concave down for $x > 0$ . $x = 0$ is a point of inflection.

There are no vertical asymptotes, since the function is defined for all x.

Observe that

$$\lim_{x \to +\infty} \dfrac{x}{\sqrt{x^2 + 7}} = 1.$$

Hence, the graph is asymptotic to $y = 1$ as $x \to +\infty$ .

You may find it surprising that

$$\lim_{x \to -\infty} \dfrac{x}{\sqrt{x^2 + 7}} = -1.$$

Actually, it is no surprise if you think about it. Since $x \to -\infty$ , x is taking on negative values. The numerator x is negative, but the denominator $\sqrt{x^2 + 7}$ is always positive (by definition of "$\sqrt{}$ "). Hence, the limit must be negative, or at least not positive.

Algebraically, this is a result of the fact that

$$\sqrt{u^2} = |u|.$$

Moreover, $|u| = -u$ if u is negative. (The absolute value of a negative number is the negative of the number.)

Here is the computation in more detail:

$$\lim_{x \to -\infty} \dfrac{x}{\sqrt{x^2 + 7}} = \lim_{x \to -\infty} \dfrac{\dfrac{1}{x}\cdot x}{\dfrac{1}{x}\cdot \sqrt{x^2 + 7}} = \lim_{x \to -\infty} \dfrac{1}{-\sqrt{\dfrac{1}{x^2}\cdot (x^2 + 7)}} = \lim_{x \to -\infty} \dfrac{1}{-\sqrt{1 + \dfrac{7}{x^2}}} = -1.$$

Notice the negative sign that appeared when I pushed the $\dfrac{1}{x}$ into the square root. This is a result of the algebraic fact I mentioned above.

Thus, the graph is asymptotic to $y = -1$ as $x \to -\infty$ .

$$\hbox{\epsfysize=2in \epsffile{rev2-2g.eps}}\quad\halmos$$

4. Graph $y = 5 x^{2/5} + \dfrac{5}{7} x^{7/5}$ .

The function is defined for all x.

$0 = y = 5 x^{2/5} + \dfrac{5}{7}x^{7/5} = 5 x^{2/5}(1 + \dfrac{1}{7}x)$ for $x = 0$ and $x = -7$ . These are the x-intercepts.

Set $x = 0$ ; the y-intercept is $y = 0$ .

The derivatives are

$$y' = 2 x^{-3/5} + x^{2/5} = x^{-3/5}(2 + x) = \dfrac{x + 2}{x^{3/5}}, \quad y'' = -\dfrac{6}{5} x^{-8/5} + \dfrac{2}{5} x^{-3/5} = \dfrac{1}{5}x^{-8/5}(-6 + 2 x) = \dfrac{1}{5}\cdot \dfrac{2(x - 3)}{x^{8/5}}.$$

$y' = \dfrac{x + 2}{x^{3/5}} = 0$ for $x = -2$ . $y'$ is undefined at $x = 0$ .

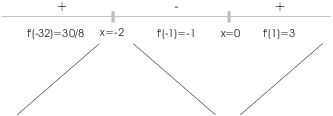
$$\hbox{\epsfxsize=3in \epsffile{rev2-3i.eps}}$$

The graph increases for $x \le -2$ and for $x \ge 0$ . The graph decreases for $-2 \le x \le 0$ .

There is a local max at $x = -2$ ; the approximate y-value is 4.71253. There is a local min at $(0, 0)$ .

Note that

$$\lim_{x \to 0-} \dfrac{x + 2}{x^{3/5}} = -\infty \quad\hbox{and}\quad \lim_{x \to 0+} \dfrac{x + 2}{x^{3/5}} = +\infty.$$

There is a vertical tangent at the origin.

$y'' = \dfrac{1}{5}\cdot \dfrac{2(x - 3)}{x^{8/5}} = 0$ at $x = 3$ and $y''$ is undefined at $x = 0$ .

$$\hbox{\epsfxsize=3in \epsffile{rev2-3c.eps}}$$

The graph is concave down for $x < 0$ and for $0 < x < 3$ . The graph is concave up for $x > 3$ . There is a point of inflection at $x = 3$ .

There are no vertical asymptotes.

$$\lim_{x \to +\infty} (5 x^{2/5} + \dfrac{5}{7}x^{7/5}) = +\infty \quad\hbox{and}\quad \lim_{x \to -\infty} (5 x^{2/5} + \dfrac{5}{7}x^{7/5}) = -\infty.$$

The graph falls to $-\infty$ on the far left and rises to $+\infty$ on the far right.

$$\hbox{\epsfysize=2in \epsffile{rev2-3g.eps}}\quad\halmos$$

5. Graph $y = \dfrac{2 x}{x^2 - 1}$ .

The domain is all x except $x = \pm 1$ .

The x-intercept is $x = 0$ ; the y-intercept is $y = 0$ .

The derivatives are

$$y' = \dfrac{(x^2 - 1)(2) - (2 x)(2 x)}{(x^2 - 1)^2} = \dfrac{-2(x^2 + 1)}{(x^2 - 1)^2},$$

$$y'' = -2\cdot \dfrac{(x^2 - 1)^2(2 x) - (x^2 + 1)(2)(x^2 - 1)(2 x)} {(x^2 - 1)^4} = \dfrac{4 x(x^2 + 3)}{(x^2 - 1)^3}.$$

$y' = \dfrac{-2(x^2 + 1)}{(x^2 - 1)^2}$ is always negative: -2 is negative, while $x^2 + 1$ and $(x^2 - 1)^2$ are always positive. The graph is decreasing everywhere; there are no local maxima or minima.

$y'' = \dfrac{4 x(x^2 + 3)}{(x^2 - 1)^3} = 0$ for $x = 0$ . $y''$ is undefined at $x = \pm 1$ .

$$\hbox{\epsfxsize=3in \epsffile{rev2-4c.eps}}$$

The graph is concave up for $-1 < x < 0$ and for $x > 1$ . The graph is concave down for $x < -1$ and for $0 < x < 1$ . $x = 0$ is the only inflection point.

There are vertical asymptotes at $x = \pm 1$ . In fact,

$$\eqalign{ \lim_{x \to 1+} \dfrac{2 x}{x^2 - 1} = +\infty, \quad & \lim_{x \to 1-} \dfrac{2 x}{x^2 - 1} = -\infty, \cr \lim_{x \to -1+} \dfrac{2 x}{x^2 - 1} = +\infty, \quad & \lim_{x \to -1-} \dfrac{2 x}{x^2 - 1} = -\infty. \cr}$$

The graph is asymptotic to $y = 0$ as $x \to +\infty$ and as $x \to -\infty$ :

$$\lim_{x \to +\infty} \dfrac{2 x}{x^2 - 1} = 0 \quad\hbox{and}\quad \lim_{x \to -\infty} \dfrac{2 x}{x^2 - 1} = 0.$$

$$\hbox{\epsfysize=2in \epsffile{rev2-4g.eps}}\quad\halmos$$

6. Graph $f(x) = (x^2 - 4 x + 5) e^x$ .

The domain is all real numbers.

Since $0 = (x^2 - 4 x + 5) e^x$ has no solutions, there are no x-intercepts.

Setting $x = 0$ gives $y = 5$ ; the y-intercept is $y = 5$ .

The derivatives are

$$f'(x) = (x^2 - 4 x + 5) e^x + (2 x - 4) e^x = (x^2 - 2 x + 1) e^x = (x - 1)^2 e^x,$$

$$f''(x) = (x^2 - 2 x + 1) e^x + (2 x - 2) e^x = (x^2 - 1) e^x = (x - 1)(x + 1) e^x.$$

$f'(x)$ is defined for all x. $f'(x) = 0$ for $x = 1$ .

$$\hbox{\epsfxsize=3in \epsffile{rev2-5i.eps}}$$

f increases for all x.

There are no local maxima or minima.

$f''(x)$ is defined for all x. $f''(x) = 0$ for $x = 1$ and $x = -1$ .

$$\hbox{\epsfxsize=3in \epsffile{rev2-5c.eps}}$$

f is concave up for $x < -1$ and for $x > 1$ . f is concave down for $-1 < x < 1$ . $x = -1$ and $x = 1$ are inflection points.

There are no vertical asymptotes, since f is defined for all x.

$$\lim_{x\to +\infty} (x^2 - 4 x + 5) e^x = +\infty \quad\hbox{and}\quad \lim_{x\to -\infty} (x^2 - 4 x + 5) e^x = 0.$$

(You can verify the second limit empirically by plugging in a large negative number for x. For example, when $x = -100$ , $(x^2 - 4 x + 5) e^x \approx 3.87074 \times 10^{-40}$ , which is pretty close to 0.)

$y = 0$ is a horizontal asymptote at $-\infty$ .

$$\hbox{\epsfysize=1.5in \epsffile{rev2-5g.eps}}\quad\halmos$$

7. Graph $f(x) = (x - 2)(x - 3) + 2 \ln x$ .

The domain is $x > 0$ .

The x-intercept is $x \approx 0.0573709$ . There are no y-intercepts.

Write

$$f(x) = x^2 - 5 x + 6 + 2\ln x.$$

The derivatives are

$$f'(x) = 2 x - 5 + \dfrac{2}{x} = \dfrac{2 x^2 - 5 x + 2}{x} = \dfrac{(2 x - 1)(x - 2)}{x},$$

$$f''(x) = 2 - \dfrac{2}{x^2} = \dfrac{2 x^2 - 2}{x^2} = \dfrac{2(x - 1)(x + 1)}{x^2}.$$

$f'(x)$ is undefined for $x = 0$ . $f'(x) = 0$ for $x = \dfrac{1}{2}$ and $x = 2$ .

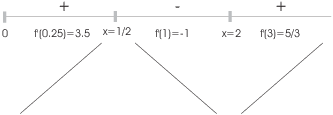
$$\hbox{\epsfxsize=3in \epsffile{rev2-6i.eps}}$$

f increases for $0 < x \le \dfrac{1}{2}$ and for $x \ge 2$ . f decreases for $\dfrac{1}{2} \le x \le 2$ .

$x = \dfrac{1}{2}$ is a local max; $x = 2$ is a local min.

$f''(x)$ is undefined for $x = 0$ . $f''(x) = 0$ for $x = 1$ and $x = -1$ ; however, $x = -1$ is not in the domain of f.

$$\hbox{\epsfxsize=3in \epsffile{rev2-6c.eps}}$$

f is concave up for $x > 1$ and concave down for $0 < x < 1$ .

$x = 1$ is an inflection point.

Note that

$$\lim_{x\to 0^+} \left((x - 2)(x - 3) + 2\ln x\right) = -\infty.$$

Thus, there is a vertical asymptote at $x = 0$ . (You can only approach 0 from the right, since f is only defined for $x > 0$ .)

Also,

$$\lim_{x\to +\infty} \left((x - 2)(x - 3) + 2\ln x\right) = +\infty.$$

Therefore, f does not have any horizontal asymptotes.

$$\hbox{\epsfysize=1.5in \epsffile{rev2-6g.eps}}\quad\halmos$$

8. Graph $f(x) = \dfrac{1}{6} \dfrac{x - 1}{(x + 1)^3}$ .

Hint: The derivatives are

$$f'(x) = -\dfrac{1}{3} \dfrac{x - 2}{(x + 1)^4} \quad\hbox{and}\quad f''(x) = \dfrac{x - 3}{(x + 1)^5}.$$

The domain is $x \ne -1$ .

The x-intercept is $x = 1$ .The y-intercept is $y = -\dfrac{1}{6}$ .

The derivatives were given in the hint, but here's how to compute them directly. By the Quotient Rule,

$$f'(x) = \dfrac{1}{6} \dfrac{(x + 1)^3 (1) - (x - 1)(3)(x + 1)^2}{(x + 1)^6} = \dfrac{1}{6} \dfrac{(x + 1) - 3 (x - 1)}{(x + 1)^4} = \dfrac{1}{6} \dfrac{-2 x + 4}{(x + 1)^4} = -\dfrac{1}{3} \dfrac{x - 2}{(x + 1)^4}.$$

Again, by the Quotient Rule,

$$f''(x) = -\dfrac{1}{3} \dfrac{(x + 1)^4 (1) - (x - 2)(4)(x + 1)^3}{(x + 1)^8} = -\dfrac{1}{3} \dfrac{(x + 1) - 4 (x - 2)}{(x + 1)^5} = -\dfrac{1}{3} \dfrac{-3 x + 9}{(x + 1)^5} = \dfrac{x - 3}{(x + 1)^5}.$$

$f'(x) = 0$ for $x = 2$ , and $f'(x)$ is undefined for $x = -1$ .

$$\hbox{\epsfxsize=1.5in \epsffile{rev2-7i.eps}}$$

f increases for $x < -1$ and for $-1 < le 2$ , and f decreases for $x \ge 2$ .

$x = 2$ is a local max.

$f''(x) = 0$ for $x = 3$ , and $f''(x)$ is undefined for $x = -1$ .

$$\hbox{\epsfxsize=1.5in \epsffile{rev2-7c.eps}}$$

f is concave up for $x < -1$ and for $x > 3$ , and f is concave down for $-1 < x < 3$ .

$x = 3$ is an inflection point.

$$\lim_{x \to \infty} \dfrac{1}{6} \dfrac{x - 1}{(x + 1)^3} = 0 \quad\hbox{and}\quad \lim_{x \to -\infty} \dfrac{1}{6} \dfrac{x - 1}{(x + 1)^3} = 0.$$

$y = 0$ is a horizontal asymptote at $\infty$ and at $-\infty$ .

$$\lim_{x \to -1^+} \dfrac{1}{6} \dfrac{x - 1}{(x + 1)^3} = -\infty \quad\hbox{and}\quad \lim_{x \to -1^-} \dfrac{1}{6} \dfrac{x - 1}{(x + 1)^3} = +\infty.$$

$x = -1$ is a vertical asymptote.

$$\hbox{\epsfysize=2in \epsffile{rev2-7g.eps}} \quad\halmos$$

9. A function $y = f(x)$ is defined for all x. In addition:

$$f(-1) = 0 \quad\hbox{and}\quad f'(3) \quad\hbox{is undefined},$$

$$f'(x) \ge 0 \quad\hbox{for}\quad x \le 2 \quad\hbox{and}\quad x > 3,$$

$$f'(x) \le 0 \quad\hbox{for}\quad 2 \le x < 3,$$

$$f''(x) < 0 \quad\hbox{for}\quad x < 3,$$

$$f''(x) > 0 \quad\hbox{for}\quad x > 3.$$

Sketch the graph of f.

Here's the sign chart for $f'$ :

$$\hbox{\epsfxsize=2.5in \epsffile{rev2-9i.eps}}$$

f increases for $x \le 2$ and for $x \ge 3$ . f decreases for $2 \le x \le 3$ . There's a local max at $x = 2$ and a local min at $x = 3$ . Note that since f is defined for all x but $f'(3)$ is undefined, there is a corner in the graph at $x = 3$ .

Here's the sign chart for $f''$ :

$$\hbox{\epsfxsize=2.5in \epsffile{rev2-9c.eps}}$$

f is concave up for $x > 3$ and concave down for $x < 3$ . There is an inflection point at $x = 3$ .

Here is a the graph of f:

$$\hbox{\epsfysize=1.75in \epsffile{rev2-9g.eps}}\quad\halmos$$

10. Sketch the graph of $y = |x^2 - 6 x + 5|$ by first sketching the graph of $y = x^2 - 6 x + 5$ .

$y = x^2 - 6 x + 5 = (x - 1)(x - 5)$ is a parabola with roots at $x = 1$ and at $x = 5$ , opening upward:

$$\hbox{\epsfysize=1.75in \epsffile{rev2-10a.eps}}$$

The absolute value function leaves the positive parts alone and reflects the negative parts about the x-axis. Hence, the graph of $y = |x^2 - 6 x + 5|$ is

$$\hbox{\epsfysize=1.75in \epsffile{rev2-10b.eps}}$$

11. Find the critical points of $y = \dfrac{1}{3}x^3 + \dfrac{3}{2}x^2 - 4 x + 5$ and classify them as local maxima or local minima using the Second Derivative Test.

$$y' = x^2 + 3 x - 4 = (x + 4)(x - 1) \quad\hbox{and}\quad y'' = 2 x + 3.$$

The critical points are $x = -4$ and $x = 1$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & x & & $y'' = 2 x + 3$ & & conclusion & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 5 & & local min & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & -4 & & -5 & & local max & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

12. Find the critical points of $y = -\dfrac{1}{x} + \dfrac{4}{x^2} - \dfrac{4}{x^3}$ and classify them as local maxima or local minima using the Second Derivative Test.

Note that

$$y = -x^{-1} + 4 x^{-2} - 4 x^{-3}.$$

So

$$\eqalign{ y & = x^{-2} - 8 x^{-3} + 12 x^{-4} \cr & = \dfrac{1}{x^2} - \dfrac{8}{x^3} + \dfrac{12}{x^4} \cr & = \dfrac{x^2 - 8 x + 12}{x^4} \cr & = \dfrac{(x - 2)(x - 6)}{x^4} \cr}$$

Hence, $y' = 0$ for $x = 2$ and for $x = 6$ .

Also,

$$y'' = -2 x^{-3} + 24 x^{-4} - 48 x^{-5}.$$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & x & & $y'' = -2 x^{-3} + 24 x^{-4} - 48 x^{-5}$ & & conclusion & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & $-\dfrac{1}{4}$ & & max & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 6 & & $\dfrac{1}{324}$ & & min & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

13. For $f(x) = \dfrac{6}{x + 1}$ , use differentials to approximate $f(2.04)$ .

I have

$$f'(x) = -\dfrac{6}{(x + 1)^2}.$$

Taking $x = 2$ gives $dx = 2.04 - 2 = 0.04$ . So

$$f(2.04) \approx f(2) + f'(2)\,dx = \dfrac{6}{2 + 1} + \left(-\dfrac{6}{(2 + 1)^2}\right)(0.04) = 2 - \dfrac{2}{75} = \dfrac{148}{75}.\quad\halmos$$

14. Suppose $y = f(x)$ is a differentiable function, $f(3) = 4$ , and $f'(3) = -6$ . Use differentials to approximate $f(3.01)$ .

Use the formula

$$f(x + dx) \approx f(x) + f'(x)\,dx.$$

Here $x = 3$ and $x + dx = 3.01$ , so

$$dx = (x + dx) - x = 3.01 - 3 = 0.01.$$

Therefore,

$$f(3.01) = f(x + dx) \approx f(x) + f'(x)\,dx = 4 + (-6)(0.01) = 4 - 0.06 = 3.94.\quad\halmos$$

15. The derivative of a function $y = f(x)$ is $y' = \dfrac{1}{x^4 + x^2 + 2}$ . Approximate the change in the function as x goes from 1 to 0.99.

$y'(1) = \dfrac{1}{1^4 + 1^2 + 2} = 0.25$ , and $dx = 0.99 - 1 = -0.01$ . The change in the function is approximately

$$dy = f'(x)\,dx = (0.25)(-0.01) = -0.0025.\quad\halmos$$

16. Use a linear approximation to approximate $\sqrt{1.99^3 + 1}$ to five decimal places.

Let $f(x) = \sqrt{x^3 + 1}$ , so $f(1.99) = \sqrt{1.99^3 + 1}$ and

$$f'(x) = \dfrac{3 x^2}{2\sqrt{x^3 + 1}}.$$

Take $x = 2$ and $x + dx = 1.99$ , so $dx = 1.99 - 2 = -0.01$ . Then

$$f(1.99) \approx f(2) + f'(2)\,dx = \sqrt{9} + \left(\dfrac{12}{6}\right)(-0.01) \approx 2.98.\quad\halmos$$

17. The area of a sphere of radius r is $A = 4 \pi r^2$ . Suppose that the radius of a sphere is measured to be 5 meters with an error of $\pm 0.2$ meters. Use a linear approximation to approximate the error in the area and the percentage error.

$$dA = A'(r)\,dr, \quad\hbox{so}\quad dA = 8 \pi r\,dr.$$

$dA$ is the approximate error in the area, and $dr$ is the approximate error in the radius. In this case, $r = 5$ and $dr = 0.2$ . (I'm neglecting the sign, since I just care about the size of the error.) Then

$$dA = 8 \pi \cdot 5 \cdot 0.2 = 8 \pi = 25.13274 \ldots.$$

The percentage area (or relative error) is approximately

$$\dfrac{dA}{A} = \dfrac{8 \pi}{4 \pi \cdot 5^2} = \dfrac{8 \pi}{100 \pi} = 0.08 = 8\%.\quad\halmos$$

18. x and y are related by the equation

$$\dfrac{x^3}{y} - 4 y^2 = 6 xy - 8 y.$$

Find the rate at which x is changing when $x = 2$ and $y = 1$ , if y decreases at 21 units per second.

Differentiate the equation with respect to t:

$$\dfrac{(y)\left(3 x^2 \der x t\right) - (x^3)\left(\der y t\right)}{y^2} - 8 y \der y t = 6 x \der y t + 6 y \der x t - 8 \der y t.$$

Plug in $x = 2$ , $y = 1$ , and $\der y t = -21$ :

$$12 \der x t + 168 + 168 = -252 + 6 \der x t + 168, \quad \der x t = -70.$$

x decreases at 70 units per second.

19. The volume of a cylinder of radius r and height h is $V = \pi r^2 h$ . Find the rate at which the volume is changing when the radius is 6 and the height is 4, if the radius increases at 2 units per second and the height decreases at 3 units per second.

Differentiate with respect to t:

$$\der V t = \pi \left(r^2 \der h t + h (2 r) \der r t\right).$$

Plug in $r = 6$ , $h = 4$ , $\der r t = 2$ , and $\der h t = -3$ . (Note that $\der h t$ is negative because h decreases.)

$$\der V t = \pi \left((36)(-3) + (4)(12)(2)\right) = -108 + 96 = -12\ \hbox{units per second}.\quad\halmos$$

20. Let x and y be the two legs of a right triangle. Suppose the area is decreasing at 3 square units per second, and x is increasing at 5 units per second. Find the rate at which y is changing when $x = 6$ and $y = 20$ .

The area of the triangle is

$$A = \dfrac{1}{2}xy.$$

Differentiate with respect to t:

$$\der A t = \dfrac{1}{2} x \der y t + \dfrac{1}{2} y \der x t.$$

I have $\der A t = -3$ , $\der x t = 5$ , $x = 6$ , and $y = 20$ :

$$-3 = \dfrac{1}{2}\cdot (6)\left(\der y t\right) + \dfrac{1}{2}\cdot (20)(5), \quad -3 = 3 \der y t + 50, \quad -53 = 3 \der y t, \quad \der y t = -\dfrac{53}{3} \quad\hbox{units per second}. \quad\halmos$$

21. A bagel (with lox and cream cheese) moves along the curve $y = x^2 + 1$ in such a way that its x-coordinate increases at 3 units per second. At what rate is its y-coordinate changing when it's at the point $(2,5)$ ?

Differentiating $y = x^2 + 1$ with respect to t, I get

$$\der y t = 2 x \der x t.$$

Plug in $x = 2$ and $\der x t = 3$ :

$$\der y t = 2\cdot 2\cdot 3 = 12 \quad\hbox{units per second}.\quad\halmos$$

22. Bonzo ties Calvin to a large helium balloon, which floats away at a constant altitude of 600 feet. Bonzo pays out the rope attached to the balloon at 3 feet per second. How rapidly is the balloon moving horizontally at the instant when 1000 feet of rope have been let out? (Assume that the rope remains taut.)

Let s be the length of the rope, and let x be the horizontal distance from the balloon to Bonzo.

$$\hbox{\epsfysize=2in \epsffile{rev2-16.eps}}$$

By Pythagoras,

$$s^2 = x^2 + 600^2.$$

Differentiate with respect to t:

$$2 s \der s t = 2 x \der x t, \quad s \der s t = x \der x t.$$

When $s = 1000$ , I have

$$x = \sqrt{1000^2 - 600^2} = 800.$$

Now $\der s t = 3$ , so

$$3000 = 800 \der x t, \quad \der x t = \dfrac{15}{4}\ \hbox{feet}/\hbox{sec}.\quad\halmos$$

23. Bonzo ties Calvin to a large helium balloon, which floats away at a constant altitude of 600 feet. Bonzo pays out the rope attached to the balloon at 3 feet per second. How rapidly is the angle between the rope and the ground changing at the instant when 1000 feet of rope have been let out? (Assume that the rope remains taut.)

Let s be the length of the rope, and let $\theta$ be the angle between the rope and the ground.

$$\hbox{\epsfysize=2in \epsffile{rev2-19.eps}}$$

I have

$$\sin \theta = \dfrac{600}{s}.$$

Differentiate with respect to t:

$$(\cos \theta) \der \theta t = -\dfrac{600}{s^2} \der s t.$$

When $s = 1000$ , the side adjacent to $\theta$ is

$$\sqrt{1000^2 - 600^2} = 800.$$

Hence, $\cos \theta = \dfrac{800}{1000}$ .

Now $\der s t = 3$ , so

$$\dfrac{800}{1000} \der \theta t = -\dfrac{600}{1000^2} \cdot 3, \quad \der \theta t = -\dfrac{9}{4000}\ \hbox{rad}/\hbox{sec}.\quad\halmos$$

24. A poster 6 feet high is mounted on a wall, with the bottom edge 5 feet above the ground. Calvin walks toward the picture at a constant rate of 2 feet per week. His eyes are level with the bottom edge of the picture. Let $\theta$ be the vertical angle subtended by the picture at Calvin's eyes. At what rate is $\theta$ changing when Calvin is 8 feet from the picture?

Let x be the distance from Calvin's eye to the base of the picture.

$$\hbox{\epsfysize=2in \epsffile{rev2-17a.eps}}$$

Now

$$\tan \theta = \dfrac{6}{x}, \quad\hbox{so}\quad (\sec \theta)^2 \der \theta t = -\dfrac{6}{x^2}\cdot \der x t.$$

Calvin walks toward the picture at 2 feet per week, so $\der x t = -2$ . (It's negative because the distance to the picture is decreasing.) When Calvin is 8 feet from the picture, $x = 8$ . At that instant, the triangle looks like this:

$$\hbox{\epsfysize=2in \epsffile{rev2-17b.eps}}$$

(I got the 10 on the hypotenuse by Pythagoras.) Thus, $\sec \theta = \dfrac{10}{8} = \dfrac{5}{4}$ , so

$$\left(\dfrac{5}{4}\right)^2 \der \theta t = -\dfrac{6}{64}\cdot (-2), \quad \der \theta t = \dfrac{3}{25}\ \hbox{feet}/\hbox{week}.\quad\halmos$$

25. Find the number(s) c satisfying the conclusion of the Mean Value Theorem for $f(x) = x^3 + 3 x + 5$ on the interval $1 \le x \le 3$ .

First,

$$f'(x) = 3 x^2 + 3, \quad\hbox{so}\quad f'(c) = 3 c^2 + 3.$$

Next,

$$\dfrac{f(3) - f(1)}{3 - 1} = \dfrac{41 - 9}{3 - 1} = 16.$$

Equate $f'(c)$ and $\dfrac{f(3) - f(1)}{3 - 1}$ and solve for c:

$$\eqalign{ 3 c^2 + 3 & = 16 \cr 3 c^2 & = 13 \cr \noalign{\vskip2 pt} c^2 & = \dfrac{13}{3} \cr \noalign{\vskip2 pt} c & = \pm \sqrt{\dfrac{13}{3}} \cr}$$

Since c should be in the interval $1 \le x \le 3$ , I reject $-\sqrt{\dfrac{13}{3}}$ . Thus, $c = \sqrt{\dfrac{13}{3}}$ .

26. Prove that the equation $x^5 + 7 x^3 + 13 x - 5 = 0$ has exactly one root.

Let $f(x) = x^5 + 7 x^3 + 13 x - 5$ . I have to show that f has exactly one root.

First, I'll show that f has at least one root. Then I'll show that it can't have more than one root.

Note that

$$f(0) = -5 \quad\hbox{and}\quad f(1) = 16.$$

By the Intermediate Value Theorem, f must have at least one root between 0 and 1.

Now suppose that f has more than one root. Then it has at least two roots, so let a and b be roots of f. Thus, $f(a) = 0$ and $f(b) = 0$ , and by Rolle's theorem, f must have a horizontal tangent between a and b.

However, the derivative is

$$f'(x) = 5 x^4 + 21 x^2 + 13.$$

Since all the powers are even and the coefficients are positive,

$$f'(x) = 5 x^4 + 21 x^2 + 13 > 0 \quad\hbox{for all}\quad x.$$

In particular, $f'(x)$ is never 0, so f has no horizontal tangents.

Since I've reached a contradiction, my assumption that f has more than one root must be wrong. Therefore, f can't have more than one root.

Since I already know f has at least one root, it must have exactly one root.

27. Suppose that f is a differentiable function, $f(3) = 10$ and $f'(x) > 7$ for all x. Prove that $f(5) > 24$ .

Apply the Mean Value Theorem to f on the interval $3 \le x \le 5$ . There is a number c such that $3 < c < 5$ and

$$\dfrac{f(5) - f(3)}{5 - 3} = f'(c).$$

Then

$$\eqalign{ \dfrac{f(5) - f(3)}{2} & = f'(c) \cr \dfrac{f(5) - 10)}{2} & = f'(c) \cr \dfrac{f(5) - 10)}{2} & = f'(c) > 7 \cr 2 \cdot \dfrac{f(5) - 10)}{2} & > 2 \cdot 7 \cr f(5) - 10 & > 14 \cr f(5) & > 24 \quad\halmos \cr}$$

28. Suppose that f is a differentiable function, $f(4) = 7$ and $|f'(x)| \le 10$ for all x. Prove that $-13 \le f(6) \le 27$ .

Applying the Mean Value Theorem to f on the interval $4 \le x \le 6$ , I find that there is a number c such that $4 < c < 6$ and

$$\dfrac{f(6) - f(4)}{6 - 4} = f'(c), \quad\hbox{or}\quad \dfrac{f(6) - 7}{2} = f'(c).$$

Thus,

$$\left|\dfrac{f(6) - 7}{2}\right| = |f'(c)| \le 10, \quad\hbox{so}\quad |f(6) - 7| \le 20.$$

The inequality says that the distance from $f(6)$ to 7 is less than or equal to 20. Since $7 - 20 = -13$ and $7 + 20 = 27$ , it follows that

$$-13 \le f(6) \le 27.\quad\halmos$$

29. Use the Mean Value Theorem to show that if $0 < x < 1$ , then

$$x + 1 < e^x < e x + 1.$$

Apply the Mean Value Theorem to $f(x) = e^x$ with $a = 0$ and $b = x$ , where $0 < x < 1$ . The theorem says that there is a number c between 0 and x such that

$$\dfrac{f(x) - f(0)}{x - 0} = f'(c).$$

Now $f(0) = e^0 = 1$ , and $f'(c) = e^c$ , so

$$\dfrac{e^x - 1}{x} = e^c.$$

Since $0 < c < x < 1$ , and since $e^x$ increases,

$$1 = e^0 < e^c < e^1 = e.$$

Therefore,

$$1 < \dfrac{e^x - 1}{x} < e, \quad\hbox{or}\quad x + 1 < e^x < e x + 1.\quad\halmos$$

30. Show graphically the result of performing two iterations of Newton's method on the function whose graph is shown below.

$$\hbox{\epsfysize=1.5in \epsffile{rev2-20s.eps}}\quad\halmos$$

31. A differentiable function satisfies $f(3) = 0.2$ and $f'(3) = 10$ . If Newton's method is applied to f starting at $x = 3$ , what is the next value of x?

$$3 - \dfrac{f(3)}{f'(3)} = 3 - \dfrac{0.2}{10} = 3 - 0.02 = 2.98.\quad\halmos$$

32. Newton's method is applied at a point c, with

$$f(c) = 21 \quad\hbox{and}\quad f'(c) = 35.$$

The new x-value is 1.4. Find c.

The Newton's method formula says

$$c - \dfrac{f(c)}{f'(c)} = 1.4.$$

So

$$\eqalign{ c - \dfrac{21}{35} & = 1.4 \cr \noalign{\vskip2 pt} c - 0.6 & = 1.4 \cr c & = 2 \quad\halmos \cr}$$

33. Use Newton's method to approximate a solution to $x^2 + 2 x = \dfrac{5}{x}$ . Do 5 iterations starting at $x = 1$ , and do your computations to at least 5-place accuracy.

Rewrite the equation:

$$\eqalign{ x^2 + 2 x & = \dfrac{5}{x} \cr \noalign{\vskip2pt} x^3 + 2 x^2 & = 5 \cr x^3 + 2 x^2 - 5 & = 0 \cr}$$

Let $f(x) = x^3 + 2 x^2 - 5$ . The Newton function is

$$[N(f)](x) = x - \dfrac{x^3 + 2 x^2 - 5}{3 x^2 + 4 x}.$$

Iterating this function starting at $x = 1$ produces the iterates

$$1,\ 1.28571,\ 1.24300,\ 1.24190,\ 1.24190.$$

The root is $x \approx 1.24190$ .

34. Find the absolute max and absolute min of $y = x^3 - 12 x + 5$ on the interval $-1 \le x \le 4$ .

The derivative is

$$y' = 3 x^2 - 12 = 3(x - 2)(x + 2).$$

$y'$ is defined for all x; $y' = 0$ for $x = 2$ or $x = -2$ . I only consider $x = 2$ , since $x = -2$ is not in the interval $-1 \le x \le 4$ . Plug the critical point and the endpoints into the function:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & x & & -1 & & 2 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & $f(x)$ & & 16 & & -11 & & 21 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The absolute max is $y = 21$ at $x = 4$ ; the absolute min is $y = -11$ at $x = 2$ .

35. Find the absolute max and absolute min of $y = 3 x^{2/3}\left(\dfrac{1}{8}x^2 - \dfrac{1}{5}x - 1\right)$ on the interval $-2 \le x \le 8$ .

First, multiply out:

$$y = \dfrac{3}{8}x^{8/3} - \dfrac{3}{5}x^{5/3} - 3 x^{2/3}.$$

(This makes it easier to differentiate.) The derivative is

$$y' = x^{5/3} - x^{2/3} - 2 x^{-1/3}.$$

Simplify by writing the negative power as a fraction, combining over a common denominator, then factoring:

$$y' = x^{5/3} - x^{2/3} - 2 x^{-1/3} = x^{5/3} - x^{2/3} - \dfrac{2}{x^{1/3}} = x^{5/3}\cdot \dfrac{x^{1/3}}{x^{1/3}} - x^{2/3}\cdot \dfrac{x^{1/3}}{x^{1/3}} - \dfrac{2}{x^{1/3}} = \dfrac{x^2 - x - 2}{x^{1/3}} = \dfrac{(x - 2)(x + 1)}{x^{1/3}}.$$

$y' = 0$ for $x = 2$ and for $x = -1$ . $y'$ is undefined for $x = 0$ . All of these points are in the interval $-2 \le x \le 8$ , so all need to be tested.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & -2 & & -1 & & 0 & & 2 & & 8 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & y & & -0.47622 & & -2.025 & & 0 & & -4.28598 & & 64.8 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The absolute max is at $x = 8$ ; the absolute min is at $x =2$ .

36. Find the absolute max and absolute min of $y = \dfrac{2}{x^2} - \dfrac{4}{x^4}$ on the interval $1 \le x \le 3$ .

$$y' = -\dfrac{4}{x^3} + \dfrac{16}{x^5} = -\dfrac{4 x^2}{x^5} + \dfrac{16}{x^5} = \dfrac{16 - 4 x^2}{x^5} = \dfrac{4(4 - x^2)}{x^5} = \dfrac{4(2 - x)(2 + x)}{x^5}.$$

$y' = 0$ for $x = 2$ and $x = -2$ . However, $x = -2$ is not in the interval $[1, 3]$ . $y'$ is undefined for $x = 0$ , but the function is undefined at $x = 0$ , and anyway $x = 0$ is not in the interval $[1, 3]$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & x & & 1 & & 2 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & $f(x)$ & & -2 & & 0.25 & & $\approx 0.17289$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The absolute min is at $x = 1$ and the absolute max is at $x = 2$ .

37. Silas Hogwinder is finding the absolute max and min of $f(x) = x^3 - 3 x + 2$ on the interval $-3 \le x \le 3$ . Silas constructs the following sign chart for $y'$ :

$$\hbox{\epsfxsize=3 in \epsffile{rev2-18.eps}}$$

He concludes that the max is at $x = -1$ and the min is at $x = 1$ . What is wrong with his reasoning?

The increasing-decreasing sign chart tells you if a point is a local max or min by the First Derivative Test. But it doesn't mean that the local max is an absolute max, or that the local min is an absolute min.

Silas should plug the critical points $x = 1$ and $x = -1$ into $f(x) = x^3 - 3 x + 1$ together with the endpoints 3 and -3. Here's what he should have gotten:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & -3 & & -1 & & 1 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $f(x)$ & & -16 & & 4 & & 0 & & 20 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Actually, the absolute max is at $x = 3$ and the absolute min is at $x = -3$ . The sign chart can't detect how far up the graph goes on the right, or how far down the graph goes on the left.

The greatest griefs are those we cause ourselves. - Sophocles

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga