Review Problems for Test 3

Math 161

These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the absence of a topic does not imply that it won't appear on the test.

1. Find the point(s) on $y = \sqrt{x}$ closest to the point $(1,0)$ .

2. Calvin Butterball wants to fence in two equal-size rectangular pens in his yard for his pet fish. (Calvin does not have much luck with pets, for some reason.) As shown in the picture below, one side of each pen will be bounded by an existing stone wall (and will therefore not require any fence).

$$\hbox{\epsfysize=1.75in \epsffile{rev3-2.eps}}$$

If Calvin has 300 feet of fence, what should the dimensions of the pens be to maximize the total area?

3. A rectangular box with a bottom and a top consists of two identical partitions which share a common wall. Each partition has a square bottom. If the total volume of the box (i.e the sum of the volumes of the two partitions) is 6272 cubic inches, what dimensions give the box which has the smallest total surface area?

4. A cylindrical can with a top and a bottom is to have a volume of $180\pi$ cubic inches. The material for the top and bottom costs 10 cents per square inch, while the material for the sides costs 3 cents per square inch. What dimensions yield a can which costs the least?

5. Calvin Butterball sits in his rowboat 9 miles from a long straight shore. Phoebe Small waits in a car at a point on shore 15 miles from the point on the shore closest to Calvin. Calvin rows to a point on the shore, then runs down the shore to the car.

(Then they drive to the shopping mall, where they purchase two rolls of duct tape,a tub of margarine, a Led Zeppelin T-shirt, two cans of Red Bull, a copy of Mother Earth News, a bowling ball, a metric hex key set, an ionic air purifier, three Cinnabons, leather pants, a 120 mm case fan, curly fries, and a bazooka.)

If Calvin can row at 4 miles per hour and run at 5 miles per hour, at what point on shore should he land in order to minimize his total travel time to the car?

6. A rectangular box with a square bottom and no top is made with 972 square inches of cardboard. What values of the length x of a side of the bottom and the height y give the box with the largest volume?

7. A rectangular poster has a total area of 288 square inches. The poster consists of a rectangular printed region, surrounded by margins 1 inch wide on the top and bottom and 2 inches wide on the left and right. What dimensions for the printed region maximize the area of the printed region?

8. Compute $\displaystyle \int \left(2 x^5 - \dfrac{1}{x^3} + \dfrac{1}{\sqrt{x}}\right)\,dx$ .

9. Compute $\displaystyle \int \left(x + \dfrac{1}{x}\right)^2\,dx$ .

10. Compute $\displaystyle \int \dfrac{1}{(\cos x)^2}\,dx$ .

11. Compute $\displaystyle \int \dfrac{\left(\dfrac{1}{x} + 1\right)^7}{x^2}\,dx$ .

12. Compute $\displaystyle \int \dfrac{x - 2}{(x^2 - 4 x + 5)^4}\,dx$ .

13. Compute $\displaystyle \int \dfrac{1}{\sqrt{x}(\sqrt{x} + 1)^3}\,dx$ .

14. Compute $\displaystyle \int \dfrac{x}{(x + 1)^{1/5}}\,dx$ .

15. Compute $\displaystyle \int \dfrac{e^{2 x}}{e^{2 x} + 1}\,dx$ .

16. Compute $\displaystyle \int \dfrac{x^3}{x^4 + 42}\,dx$ .

17. Compute $\displaystyle \int (\csc x)^5 \cot x\,dx$ .

18. Compute $\displaystyle \int \dfrac{\sin x}{(\cos x + 1)^2}\,dx$ .

19. Compute $\displaystyle \int (x^2 + 1){\root 3 \of {x + 1}}\,dx$ .

20. Compute $\displaystyle \int \tan 5 x\,dx$ .

21. Compute $\displaystyle \int \csc (7 x + 11)\cot (7 x + 11)\,dx$ .

22. Compute $\displaystyle \int \left(3 x^7 + 3 \cdot 7^x + 3 \cdot 7^7\right)\,dx$ .

23. Compute $\displaystyle \int (x^2 - 1)(x^2 + 3)\,dx$ .

24. Compute $\displaystyle \int \dfrac{(2 x - 1)^2}{x}\,dx$ .

25. Compute $\displaystyle \int (7 x - 5)^{43}\,dx$ .

26. Compute $\displaystyle \int \dfrac{e^{3 x} + e^{-3 x}}{e^{3 x} - e^{-3 x}}\,dx$ .

27. Compute $\displaystyle \int \left((\sin 5 x)^4 - 6 \sin 5 x + 11\right)\cos 5 x\,dx$ .

28. Compute $\displaystyle \int \dfrac{f'(x) \ln f(x)}{f(x)}\,dx$ .

29. Compute $\displaystyle \int (f(x) g'(x) + g(x) f'(x))\,dx$ .

30. Compute $\displaystyle \int (3 x + 10)(x - 4)^{20}\,dx$ .

31. Compute $\displaystyle \int \dfrac{(x + 1)^2}{\sqrt{x + 3}}\,dx$ .

32. Compute $\displaystyle \int \dfrac{x - 3}{\sqrt{x^2 - 6 x + 5}}\,dx$ .

33. Compute $\displaystyle \int \dfrac{7}{e^{5 x}}\,dx$ .

34. Compute $\displaystyle \int \dfrac{3}{\sec x}\,dx$ .

35. Compute $\displaystyle \int \dfrac{5}{e^{4 x} + 7}\,dx$ .

36. Compute $\displaystyle \int x e^{x^2} e^{(e^{x^2})}\,dx$ .

37. Compute $\displaystyle \int \left((\cos 7 x)^2 - (\sin 7 x)^2\right)\,dx$ .

38. Compute 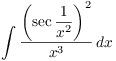$\displaystyle \int \dfrac{\left(\sec \dfrac{1}{x^2}\right)^2}{x^3}\,dx$ .

39. Compute $\displaystyle \int (e^{3 x} - 2 e^{-x})(4 e^{5 x} + e^{3 x})\,dx$ .

40. Compute $\displaystyle \int \left(x\cos (x^2 + 4) - 5 x^2 \sin (x^3 + 2)\right)\,dx$ .

41. Use a calculating device to approximate the following sum to at least three decimal places:

$$\dfrac{1}{3 + 1^2} + \dfrac{2}{3 + 2^2} + \dfrac{3}{3 + 3^2} + \cdots + \dfrac{47}{3 + 47^2}$$

42. Write the series in summation form:

(a) $\dfrac{2}{5} + \dfrac{3}{5^2} + \dfrac{4}{5^3} + \cdots + \dfrac{100}{5^{99}}$ .

(b) $\sqrt{3} \cdot \sin 4 + \sqrt{4} \cdot \sin 9 + \sqrt{5} \cdot \sin 16 + \cdots + \sqrt{100} \cdot \sin(99^2)$ .

43. (a) Express the following sum in terms of n: $\displaystyle \sum_{k=1}^n (2 - 5 k + 7 k^2)$ .

(b) Find the exact value of $\displaystyle \sum_{n=1}^{1000} (n^2 + 5 n - 7)$ .

44. (a) Verify that

$$\dfrac{1}{k^2 - k} = \dfrac{1}{k - 1} - \dfrac{1}{k}.$$

(b) Use the result of (a) to evaluate $\displaystyle \sum_{k=2}^{1000} \dfrac{1}{k^2 - k}$ .

45. Approximate $\displaystyle \int_1^5 \dfrac{\sin x}{x}\,dx$ using 10 rectangles of equal width and using the left-hand endpoint of each subinterval to obtain the rectangles' heights.

46. Approximate $\displaystyle \int_1^5 \dfrac{\sin x}{x}\,dx$ using 10 rectangles of equal width and using the right-hand endpoint of each subinterval to obtain the rectangles' heights.

47. Approximate $\displaystyle \int_1^5 \dfrac{\sin x}{x}\,dx$ using 10 rectangles of equal width and using the midpoint of each subinterval to obtain the rectangles' heights.

48. Some values for a function $y = f(x)$ are shown below.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & x & & $f(x)$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 0 & & 1.00 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 0.2 & & 1.30 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 0.4 & & 1.58 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 0.6 & & 1.86 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 0.8 & & 2.14 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.0 & & 2.41 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.2 & & 2.68 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.4 & & 2.95 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.6 & & 3.21 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.8 & & 3.47 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 2.0 & & 3.73 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

(a) Approximate $\displaystyle \int_0^2 f(x)\,dx$ using 5 rectangles of equal width and using the left-hand endpoints to obtain the rectangle heights.

(b) Approximate $\displaystyle \int_0^2 f(x)\,dx$ using 10 rectangles of equal width and using the right-hand endpoints to obtain the rectangle heights.

49. Compute $\displaystyle \int_2^4 (2 x + 3)\,dx$ by writing the integral as the limit of a rectangle sum.

50. (a) Given that $\displaystyle \der {} x \dfrac{x^2 - 2 x + 5}{x^2 - 4 x + 5} = \dfrac{2(5 - x)^2}{(x^2 - 4 x + 5)^2}$ , what is $\displaystyle \int \dfrac{2(5 - x)^2}{(x^2 - 4 x + 5)^2}\,dx$ ?

(b) Compute $\displaystyle \int \left(\der {} x \sqrt{x^4 + x^2 + 1}\right)\,dx$ .

51. Compute $\displaystyle \int_{-1}^2 (x^2 + 1)^2\,dx$ .

52. Compute $\displaystyle \int_0^1 \dfrac{2 x^3 + x}{x^4 + x^2 + 3}\,dx$ .

53. Compute $\displaystyle \int_1^2 \dfrac{x + 2}{(x^2 + 4 x + 1)^2}\,dx$ .

54. Suppose that $f''(x) = 12 x + 6$ , $f'(0) = 3$ , and $f(1) = 5$ . Find $f(x)$ .

55. Find functions $f(x)$ and $g(x)$ such that the antiderivative of $f(x) \cdot g(x)$ is not equal to the antiderivative of $f(x)$ times the antiderivative of $g(x)$ .

56. Compute $\displaystyle \int_{-1}^1 (1 - |x|)\,dx$ .

57. Compute the exact value of $\displaystyle \int_{-10}^{10} (5 + \sqrt{100 - x^2})\,dx$ .

58. Compute the exact value of $\displaystyle \int_{-1}^7 \sqrt{7 + 6 x - x^2}\,dx$ .

Hint: Complete the square in x.

59. Find the total area of the region bounded by $y = x(x - 2)(x - 4)$ and the x-axis.

60. Find the area of the region bounded by

$$x = y^2 - 9 \quad\hbox{and}\quad x = 2 y + 6.$$

61. Find the area of the region in the first quadrant bounded on the left by $y = 1 - x^2$ , on the right by $y = 1 - \dfrac{x^2}{2}$ , and below by the x-axis.

62. Find the area of the region bounded by the graphs of $y = 1 - x^2$ and $y = -1 - x$ .

63. Find the area of the region between $y = -x^2$ and $y = x - 6$ , from $x = 0$ to $x = 3$ .

64. (a) Compute $\displaystyle \der {} x \int_{-17}^x \dfrac{\cos t}{t^4 + 1}\,dt$ .

(b) Compute $\displaystyle \der {} x \int_{42}^{\sin x} \sqrt{t^2 + 2}\,dt$ .

(c) Compute $\displaystyle \der {} x \int_{e^x}^{13} \dfrac{t}{2 + \sin t}\,dt$ .

65. (a) Prove that $\displaystyle \int_0^{0.5} \dfrac{x^2}{x^2 + 1}\,dx \le 0.5$ .

(b) Use the Integral Mean Value Theorem to estimate $\displaystyle \int_0^1 e^{x^4}\,dx$ .

Solutions to the Review Problems for Test 3

1. Find the point(s) on $y = \sqrt{x}$ closest to the point $(1,0)$ .

Draw a picture. Label the things that are relevant to the problem.

$$\hbox{\epsfysize=1.75in \epsffile{rev3-1.eps}}$$

Write down an expression for the thing you're trying to maximize or minimize.

The distance from $(1,0)$ to $(x,\sqrt{x})$ is

$$d = \sqrt{(x - 1)^2 + (\sqrt{x} - 0)^2} = \sqrt{(x - 1)^2 + x}.$$

A distance is smallest exactly when its square is smallest. So we can work with the square of the distance instead:

$$D = (x - 1)^2 + x.$$

This has the advantage of removing the square root and making it easier to differentiate.

Look at the extreme cases to determine any endpoints.

x can be as small as 0, but it can be arbitrarily large. That is, $0 \le x < \infty$ .

Therefore,

$$\der D x = 2(x - 1) + 1, \quad \dfrac{d^2 D}{dx^2} = 2.$$

$\der D x = 2(x - 1) + 1 = 0$ for $x = \dfrac{1}{2}$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & x & & 0 & & $\dfrac{1}{2}$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & D & & 1 & & $\dfrac{3}{4}$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The minimum does not occur at $x = 0$ . To show that $x = \dfrac{1}{2}$ is an absolute min, notice that $\dfrac{d^2 D}{dx^2} = 2 > 0$ . Therefore, $x = 1$ is a local min. It is the only critical point, so it is an absolute min.

The closest point to $(1, 0)$ on the curve $y = \sqrt{x}$ is the point $\left(\dfrac{1}{2},\sqrt{\dfrac{1}{2}}\right)$ .

2. Calvin Butterball wants to fence in two equal-size rectangular pens in his yard for his pet fish. (Calvin does not have much luck with pets, for some reason.) As shown in the picture below, one side of each pen will be bounded by an existing stone wall (and will therefore not require any fence).

$$\hbox{\epsfysize=1.75in \epsffile{rev3-2.eps}}$$

If Calvin has 300 feet of fence, what should the dimensions of the pens be to maximize the total area?

The area is $A = 2 x y$ . The amount of fence is $300 = 2 x + 3 y$ , so $2 x = 300 - 3 y$ . Therefore,

$$A = (300 - 3 y) y = 300 y - 3 y^2.$$

The endpoints are $y = 0$ and $y = 100$ (i.e. $0 \le y \le 100$ ).

The derivative is

$$\der A y = 300 - 6 y.$$

$\der A y = 0$ for $y = 50$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & y & & 0 & & 50 & & 100 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & A & & 0 & & 7500 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$y = 50$ gives the absolute max; $x = \dfrac{1}{2}(300 - 3 y) = 75$ .

3. A rectangular box with a bottom and a top consists of two identical partitions which share a common wall. Each partition has a square bottom. If the total volume of the box (i.e the sum of the volumes of the two partitions) is 6272 cubic inches, what dimensions give the box which has the smallest total surface area?

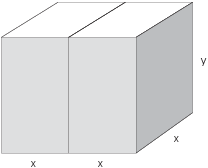
$$\hbox{\epsfysize=1.5in \epsffile{rev3-3.eps}}$$

Suppose the square base of a partition has sides of length x, and let y be the height of the box.

The total surface area is

$$A = (\hbox{bottom and top}) + (\hbox{back and front}) + (\hbox{sides and middle}) = 4 x^2 + 4 x y + 3 x y = 4 x^2 + 7 x y.$$

The volume is

$$6272 = 2 x^2 y, \quad\hbox{so}\quad y = \dfrac{6272}{2 x^2} = \dfrac{3136}{x^2}.$$

Plug this into A and simplify:

$$A = 4 x^2 + 7 x\cdot \dfrac{3136}{x^2} = 4 x^2 + \dfrac{21952}{x}.$$

The only restriction on x is $x > 0$ .

The derivatives are

$$A' = 8 x - \dfrac{21952}{x^2}, \quad A'' = 8 + \dfrac{43904}{x^3}.$$

$A'$ is defined for all $x > 0$ . Set $A' = 0$ and solve:

$$\eqalign{ 8 x - \dfrac{21952}{x^2} & = 0 \cr \noalign{\vskip2pt} 8 x & = \dfrac{21952}{x^2} \cr \noalign{\vskip2pt} x^3 & = 2744 \cr \noalign{\vskip2pt} x & = 14 \cr}$$

The corresponding value for y is $y = 16$ .

$$A''(14) = 8 + \dfrac{43904}{14^3} = 24 > 0.$$

Hence, $x = 14$ is a local min. Since it's the only critical point, it's an absolute min.

4. A cylindrical can with a top and a bottom is to have a volume of $180\pi$ cubic inches. The material for the top and bottom costs 10 cents per square inch, while the material for the sides costs 3 cents per square inch. What dimensions yield a can which costs the least?

$$\hbox{\epsfysize=1.75in \epsffile{rev3-4.eps}}$$

Let r be the radius of the can, and let h be the height.

The total cost is the cost of the sides plus the cost of the top and bottom:

$$C = (3)(2 \pi r h) + (10)(2 \pi r^2) = 6 \pi r h + 20 \pi r^2.$$

The volume is $180\pi$ , so

$$180 \pi = \pi r^2 h, \quad\hbox{and}\quad h = \dfrac{180}{r^2}.$$

Plug $h = \dfrac{180}{r^2}$ into C and simplify:

$$C = 6 \pi r \cdot \dfrac{180}{r^2} + 20 \pi r^2 = \dfrac{1080 \pi}{r} + 20 \pi r^2.$$

The only restriction on r is that $r > 0$ . Since I don't have two endpoints, I'll use the Second Derivative Test. Differentiate:

$$C' = -\dfrac{1080 \pi}{r^2} + 40 \pi r, \quad C'' = \dfrac{2160 \pi}{r^3} + 40 \pi.$$

Find the critical points:

$$\eqalign{ -\dfrac{1080 \pi}{r^2} + 40 \pi r & = 0 \cr \noalign{\vskip2pt} 40 \pi r & = \dfrac{1080 \pi}{r^2} \cr \noalign{\vskip2pt} r^3 & = 27 \cr r & = 3 \cr}$$

This gives $h = \dfrac{180}{9} = 20$ . Now

$$C''(3) = \dfrac{2160 \pi}{27} + 40\pi = 120 \pi > 0.$$

Hence, $r = 3$ is a local min. Since it's the only critical point, it must give an absolute min.

5. Calvin Butterball sits in his rowboat 9 miles from a long straight shore. Phoebe Small waits in a car at a point on shore 15 miles from the point on the shore closest to Calvin. Calvin rows to a point on the shore, then runs down the shore to the car.

(Then they drive to the shopping mall, where they purchase two rolls of duct tape,a tub of margarine, a Led Zeppelin T-shirt, two cans of Red Bull, a copy of Mother Earth News, a bowling ball, a metric hex key set, an ionic air purifier, three Cinnabons, leather pants, a 120 mm case fan, curly fries, and a bazooka.)

If Calvin can row at 4 miles per hour and run at 5 miles per hour, at what point on shore should he land in order to minimize his total travel time to the car?

$$\hbox{\epsfysize=1.75in \epsffile{rev3-5.eps}}$$

Let x be the distance from the point on shore closest to Calvin to the point where he lands. The distance that he rows is $\sqrt{x^2 + 81}$ , and the distance that he runs is $15 - x$ . Since the time elapsed is equal to the distance divided by the speed, his total travel time is

$$T = \dfrac{\sqrt{x^2 + 81}}{4} + \dfrac{15 - x}{5}.$$

(The first term is his rowing distance divided by his rowing speed, and the second term is his running distance divided by his running speed.)

The endpoints are $x = 0$ (where he rows to the nearest point on the shore) and $x = 15$ (where he rows directly to Phoebe).

Differentiate:

$$T' = \dfrac{1}{4}\cdot \dfrac{1}{2}(x^2 + 81)^{-1/2}(2 x) - \dfrac{1}{5} = \dfrac{x}{4\sqrt{x^2 + 81}} - \dfrac{1}{5}.$$

Find the critical points by setting $T' = 0$ :

$$\eqalign{ \dfrac{x}{4\sqrt{x^2 + 81}} - \dfrac{1}{5} & = 0 \cr \noalign{\vskip2pt} \dfrac{x}{4\sqrt{x^2 + 81}} & = \dfrac{1}{5} \cr \noalign{\vskip2pt} 5 x & = 4\sqrt{x^2 + 81} \cr 25 x^2 & = 16(x^2 + 81) \cr 25 x^2 & = 16 x^2 + 1296 \cr 9 x^2 & = 1296 \cr x^2 & = 144 \cr x & = 12 \cr}$$

(I omitted $x = -12$ because it isn't in the interval $0 \le x \le 15$ .)

Test the critical point and the end points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 12 & & 15 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & T & & 5.25 & & 4.35 & & $\approx 4.37321$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

He should row to a point 12 miles from the point closest to shore to minimize his travel time.

6. A rectangular box with a square bottom and no top is made with 972 square inches of cardboard. What values of the length x of a side of the bottom and the height y give the box with the largest volume?

$$\hbox{\epsfysize=1.5in \epsffile{rev3-6.eps}}$$

The volume is

$$V = x^2 y.$$

The area of the 4 sides is $4 x y$ , and the area of the bottom is $x^2$ . So

$$972 = 4 x y + x^2.$$

Solving for y gives

$$y = \dfrac{972 - x^2}{4 x}.$$

Plug this into V and simplify:

$$V = x^2 \cdot \dfrac{972 - x^2}{4 x} = \dfrac{1}{4} x (972 - x^2) = \dfrac{1}{4} (972 x - x^3).$$

Note that $x \ne 0$ , since $x = 0$ plugged into $972 = 4 x y + x^2$ gives $972 = 0$ a contradiction. So the only restriction on x is that $x > 0$ .

Since x is not restricted to a closed interval $[a, b]$ , I'll use the Second Derivative Test.

Compute the derivatives:

$$V' = \dfrac{1}{4} (972 - 3 x^2).$$

$$V'' = \dfrac{1}{4} \cdot (-6 x) = -\dfrac{3}{2} x.$$

Find the critical points:

$$\eqalign{ \dfrac{1}{4} (972 - 3 x^2) & = 0 \cr \noalign{\vskip2 pt} 972 - 3 x^2 & = 0 \cr 3 x^2 & = 972 \cr \noalign{\vskip2 pt} x^2 & = 324 \cr x & = \pm 18 \cr}$$

Since x is a length, it must be positive, so $x = 18$ . This gives

$$y = \dfrac{972 - 324}{72} = 9.$$

Plug $x = k$ into the Second Derivative:

$$V''(k) = -\dfrac{3}{2} \cdot 18 = -27 < 0.$$

$x = 18$ is a local max, but it's the only critical point, so it's an absolute max.

7. A rectangular poster has a total area of 288 square inches. The poster consists of a rectangular printed region, surrounded by margins 1 inch wide on the top and bottom and 2 inches wide on the left and right. What dimensions for the printed region maximize the area of the printed region?

The x be the width of the printed region, and let y be the height. The area of the printed region is

$$A = x y.$$

$$\hbox{\epsfysize=1.5 in \epsffile{rev3-7.eps}}$$

The total area of the poster is 288. The width is $x + 4$ and the height is $y + 2$ , so

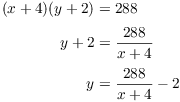
$$\eqalign{ (x + 4)(y + 2) & = 288 \cr \noalign{\vskip2 pt} y + 2 & = \dfrac{288}{x + 4} \cr \noalign{\vskip2 pt} y & = \dfrac{288}{x + 4} - 2 \cr}$$

Substituting this in A, I get

$$\eqalign{ A & = x \left(\dfrac{288}{x + 4} - 2\right) \cr \noalign{\vskip2 pt} A & = \dfrac{288 x}{x + 4} - 2 x \cr}$$

The extreme cases are $x = 0$ and $y = 0$ ; plugging $y = 0$ into $(x + 4)(y + 2) = 288$ gives $x = 140$ . So the endpoints are $x = 0$ and $x = 140$ .

$$A' = 288 \cdot \dfrac{(x + 4)(1) - (x)(1)}{(x + 4)^2} - 2 = \dfrac{1152}{(x + 4)^2} - 2.$$

Set $A' = 0$ and solve for x:

$$\eqalign{ \dfrac{1152}{(x + 4)^2} - 2 & = 0 \cr \noalign{\vskip2 pt} \dfrac{1152}{(x + 4)^2} & = 2 \cr \noalign{\vskip2 pt} 1152 & = 2(x + 4)^2 \cr 576 & = (x + 4)^2 \cr \pm 24 & = x + 4 \cr}$$

$-24 = x + 4$ gives $x = -28$ , but a width can't be negative. $24 = x + 4$ gives $x = 20$ . Plugging this into $(x + 4)(y + 2) = 288$ gives $y = 10$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 20 & & 70 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & A & & 0 & & 200 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$x = 20$ gives an absolute max. The area is maximized when $x = 20$ and $y = 10$ .

8. Compute $\displaystyle \int \left(2 x^5 - \dfrac{1}{x^3} + \dfrac{1}{\sqrt{x}}\right)\,dx$ .

$$\int \left(2 x^5 - \dfrac{1}{x^3} + \dfrac{1}{\sqrt{x}}\right)\,dx = \dfrac{1}{3} x^6 + \dfrac{1}{2 x^2} + 2\sqrt{x} + C.\quad\halmos$$

9. Compute $\displaystyle \int \left(x + \dfrac{1}{x}\right)^2\,dx$ .

$$\int \left(x + \dfrac{1}{x}\right)^2\,dx = \int\left(x^2 + 2 + \dfrac{1}{x^2}\right)\,dx = \dfrac{1}{3}x^3 + 2 x - \dfrac{1}{x} + C.\quad\halmos$$

10. Compute $\displaystyle \int \dfrac{1}{(\cos x)^2}\,dx$ .

$$\int \dfrac{1}{(\cos x)^2}\,dx = \int (\sec x)^2\,dx = \tan x + C.\quad\halmos$$

11. Compute $\displaystyle \int \dfrac{\left(\dfrac{1}{x} + 1\right)^7}{x^2}\,dx$ .

$$\int \dfrac{\left(\dfrac{1}{x} + 1\right)^7}{x^2}\,dx = -\int u^7\,du = -\dfrac{1}{8} u^8 + C = -\dfrac{1}{8} \left(\dfrac{1}{x} + 1\right)^8 + C.$$

$$\left[u = \dfrac{1}{x} + 1 \quad du = -\dfrac{1}{x^2}\,dx, \quad dx = -x^2\,du\right]\quad\halmos$$

12. Compute $\displaystyle \int \dfrac{x - 2}{(x^2 - 4 x + 5)^4}\,dx$ .

$$\int \dfrac{x - 2}{(x^2 - 4 x + 5)^4}\,dx = \dfrac{1}{2} \int u^{-4}\,du = -\dfrac{1}{6} u^{-3} + C = -\dfrac{1}{6} \dfrac{1}{(x^2 - 4 x + 5)^3} + C.$$

$$\left[u = x^2 - 4 x + 5 \quad du = (2 x - 4)\,dx = 2(x - 2)\,dx, \quad dx = \dfrac{du}{2(x - 2)}\right]\quad\halmos$$

13. Compute $\displaystyle \int \dfrac{1}{\sqrt{x}(\sqrt{x} + 1)^3}\,dx$ .

$$\int \dfrac{1}{\sqrt{x}(\sqrt{x} + 1)^3}\,dx = 2 \int u^{-3}\,du = -u^{-2} + C = -\dfrac{1}{(\sqrt{x} + 1)^2} + C.$$

$$\left[u = \sqrt{x} + 1 \quad du = \dfrac{1}{2 \sqrt{x}}\,dx, \quad dx = 2 \sqrt{x}\,du\right]\quad\halmos$$

14. Compute $\displaystyle \int \dfrac{x}{(x + 1)^{1/5}}\,dx$ .

$$\int \dfrac{x}{(x + 1)^{1/5}}\,dx = \int \dfrac{u - 1}{u^{1/5}}\,du =$$

$$\left[u = x + 1 \quad du = dx\right]$$

$$\int (u^{4/5} - u^{-1/5})\,du = \dfrac{5}{9} u^{9/5} - \dfrac{5}{4} u^{4/5} + C = \dfrac{5}{9} (x + 1)^{9/5} - \dfrac{5}{4} (x + 1)^{4/5} + C.\quad\halmos$$

15. Compute $\displaystyle \int \dfrac{e^{2 x}}{e^{2 x} + 1}\,dx$ .

$$\int \dfrac{e^{2 x}}{e^{2 x} + 1}\,dx = \dfrac{1}{2} \int \dfrac{du}{u} = \dfrac{1}{2} \ln |u| + C = \dfrac{1}{2} \ln |e^{2 x} + 1| + C.$$

$$\left[u = e^{2 x} + 1, \quad du = 2 e^{2 x}\,dx, \quad dx = \dfrac{du}{2 e^{2 x}}\right]\quad\halmos$$

16. Compute $\displaystyle \int \dfrac{x^3}{x^4 + 42}\,dx$ .

$$\int \dfrac{x^3}{x^4 + 42}\,dx = \dfrac{1}{4} \int \dfrac{du}{u} = \dfrac{1}{4} \ln |u| + C = \dfrac{1}{4} \ln |x^4 + 42| + C.$$

$$\left[u = x^4 + 42, \quad du = 4 x^3\,dx, \quad dx = \dfrac{du}{4 x^3}\right]\quad\halmos$$

17. Compute $\displaystyle \int (\csc x)^5 \cot x\,dx$ .

$$\int (\csc x)^5 \cot x\,dx = -\int u^4\,du = -\dfrac{1}{5} u^5 + C = -\dfrac{1}{5} (\csc x)^5 + C.$$

$$\left[u = \csc x \quad du = -\csc x \cot x\,dx, \quad dx = -\dfrac{du}{\csc x \cot x}\right]\quad\halmos$$

18. Compute $\displaystyle \int \dfrac{\sin x}{(\cos x + 1)^2}\,dx$ .

$$\int \dfrac{\sin x}{(\cos x + 1)^2}\,dx = \int \dfrac{\sin x}{u^2}\cdot \dfrac{du}{-\sin x} = -\int \dfrac{du}{u^2} = \dfrac{1}{u} + C = \dfrac{1}{\cos x + 1} + C.$$

$$\left[u = \cos x + 1, \quad du = -\sin x\,dx, \quad dx = \dfrac{du}{-\sin x}\right]\quad\halmos$$

19. Compute $\displaystyle \int (x^2 + 1){\root 3 \of {x + 1}}\,dx$ .

$$\int (x^2 + 1){\root 3 \of {x + 1}}\,dx \int \left((u - 1)^2 + 1\right){\root 3 \of u}\,du = \int (u^2 - 2 u + 2)u^{1/3}\,du = \int (u^{7/3} - 2 u^{4/3} + 2 u^{1/3})\,du =$$

$$\left[u = x + 1, \quad du = dx; \quad x = u - 1\right]$$

$$\dfrac{3}{10} u^{10/3} - \dfrac{6}{7} u^{7/3} + \dfrac{3}{2} u^{4/3} + C = \dfrac{3}{10} (x + 1)^{10/3} - \dfrac{6}{7} (x + 1)^{7/3} + \dfrac{3}{2} (x + 1)^{4/3} + C.\quad\halmos$$

20. Compute $\displaystyle \int \tan 5 x\,dx$ .

$$\int \tan 5 x\,dx = \int \dfrac{\sin 5 x}{\cos 5 x}\,dx = \int \dfrac{\sin 5 x}{u}\cdot \dfrac{du}{-5\sin 5 x} = -\dfrac{1}{5} \int \dfrac{du}{u} = -\dfrac{1}{5} \ln |u| + C = -\dfrac{1}{5} \ln |\cos 5 x| + C.$$

$$\left[u = \cos 5 x, \quad du = -5\sin 5 x\,dx, \quad dx = \dfrac{du}{-5\sin 5 x}\right]\quad\halmos$$

21. Compute $\displaystyle \int \csc (7 x + 11)\cot (7 x + 11)\,dx$ .

$$\int \csc (7 x + 11)\cot (7 x + 11)\,dx = \int \csc u \cot u\cdot \dfrac{du}{7} = \dfrac{1}{7} \int \csc u \cot u\,du = -\dfrac{1}{7} \csc u + C = -\dfrac{1}{7} \csc (7 x + 11) + C.$$

$$\left[u = 7 x + 11, \quad du = 7\,dx, \quad dx = \dfrac{du}{7}\right] \quad\halmos$$

22. Compute $\displaystyle \int \left(3 x^7 + 3 \cdot 7^x + 3 \cdot 7^7\right)\,dx$ .

$$\int \left(3 x^7 + 3\cdot 7^x + 3\cdot 7^7\right)\,dx = \dfrac{3}{8} x^8 + \dfrac{3}{\ln 7} 7^x + (3 \cdot 7^7) x + C.\quad\halmos$$

23. Compute $\displaystyle \int (x^2 - 1)(x^2 + 3)\,dx$ .

$$\int (x^2 - 1)(x^2 + 3)\,dx = \int (x^4 + 2 x^2 - 3)\,dx = \dfrac{1}{5} x^5 + \dfrac{2}{3} x^3 - 3 x + C.\quad\halmos$$

24. Compute $\displaystyle \int \dfrac{(2 x - 1)^2}{x}\,dx$ .

$$\int \dfrac{(2 x - 1)^2}{x}\,dx = \int \dfrac{4 x^2 - 4 x + 1}{x}\,dx = \int \left(4 x - 4 + \dfrac{1}{x}\right)\,dx = 2 x^2 - 4 x + \ln |x| + C.\quad\halmos$$

25. Compute $\displaystyle \int (7 x - 5)^{43}\,dx$ .

$$\int (7 x - 5)^{43}\,dx = \dfrac{1}{7} \int u^{43}\,du = \dfrac{1}{308} u^{44} + C = \dfrac{1}{308} (7 x - 5)^{44} + C.$$

$$\left[u = 7 x - 5 \quad du = 7\,dx, \quad dx = \dfrac{du}{7}\right] \quad\halmos$$

26. Compute $\displaystyle \int \dfrac{e^{3 x} + e^{-3 x}}{e^{3 x} - e^{-3 x}}\,dx$ .

$$\int \dfrac{e^{3 x} + e^{-3 x}}{e^{3 x} - e^{-3 x}}\,dx = \int \dfrac{e^{3 x} + e^{-3 x}}{u}\cdot \dfrac{du} {3(e^{3 x} + e^{-3 x})\,dx} = \dfrac{1}{3} \int \dfrac{du}{u} = \dfrac{1}{3} \ln |u| + C = \dfrac{1}{3} \ln |e^{3 x} - e^{-3 x}| + C.$$

$$\left[u = e^{3 x} - e^{-3 x}, \quad du = (3 e^{3 x} + 3 e^{-3 x})\,dx = 3 (e^{3 x} + e^{-3 x})\,dx, \quad dx = \dfrac{du}{3 (e^{3 x} + e^{-3 x})\,dx}\right]\quad\halmos$$

27. Compute $\displaystyle \int \left((\sin 5 x)^4 - 6 \sin 5 x + 11\right)\cos 5 x\,dx$ .

$$\int \left((\sin 5 x)^4 - 6 \sin 5 x + 11\right)\cos 5 x\,dx = \int \left(u^4 - 6 u + 11\right)(\cos 5 x)\cdot \dfrac{du}{5\cos 5 x} = \dfrac{1}{5} \int (u^4 - 6 u + 11)\,du =$$

$$\left[u = \sin 5 x, \quad du = 5\cos 5 x\,dx, \quad dx = \dfrac{du}{5\cos 5 x}\right]$$

$$\dfrac{1}{5} \left(\dfrac{1}{5}u^5 - 3 u^2 + 11 u\right) + C = \dfrac{1}{5} \left(\dfrac{1}{5} (\sin 5 x)^5 - 3 (\sin 5 x)^2 + 11 (\sin 5 x)\right) + C.\quad\halmos$$

28. Compute $\displaystyle \int \dfrac{f'(x) \ln f(x)}{f(x)}\,dx$ .

$$\int \dfrac{f'(x) \ln f(x)}{f(x)}\,dx = \int \dfrac{f'(x) \cdot u}{f(x)} \cdot \dfrac{f(x)}{f'(x)}\,du = \int u\,du = \dfrac{1}{2}u^2 + C = \dfrac{1}{2} (\ln f(x))^2 + C.$$

$$\left[u = \ln f(x), \quad du = \dfrac{f'(x)}{f(x)}\,dx, \quad dx = \dfrac{f(x)}{f'(x)}\,du\right]\quad\halmos$$

29. Compute $\displaystyle \int (f(x) g'(x) + g(x) f'(x))\,dx$ .

The Product Rule says that

$$\der {} x f(x) g(x) = f(x) g'(x) + g(x) f'(x).$$

Hence,

$$\int (f(x) g'(x) + g(x) f'(x))\,dx = f(x) g(x) + C.\quad\halmos$$

30. Compute $\displaystyle \int (3 x + 10)(x - 4)^{20}\,dx$ .

$$\int (3 x + 10)(x - 4)^{20}\,dx = \int \left(3 (u + 4) + 10\right)u^{20}\,du = \int (3 u + 22) u^{20}\,du = \int (3 u^{21} + 22 u^{20})\,du =$$

$$\left[u = x - 4, \quad du = dx, \quad x = u + 4\right]$$

$$\dfrac{3}{22} u^{22} + \dfrac{22}{21} u^{21} + C = \dfrac{3}{22} (x - 4)^{22} + \dfrac{22}{21} (x - 4)^{21} + C.\quad\halmos$$

31. Compute $\displaystyle \int \dfrac{(x + 1)^2}{\sqrt{x + 3}}\,dx$ .

$$\int \dfrac{(x + 1)^2}{\sqrt{x + 3}}\,dx = \int \dfrac{\left((u - 3) + 1\right)^2}{\sqrt{u}}\,du = \int \dfrac{(u - 2)^2}{\sqrt{u}}\,du = \int \dfrac{u^2 - 4 u + 4}{\sqrt{u}}\,du =$$

$$\left[u = x + 3, \quad du = dx, \quad x = u - 3\right]$$

$$\int \left(u^{3/2} - 4 u^{1/2} + 4 u^{-1/2}\right)\,du = \dfrac{2}{5} u^{5/2} - \dfrac{8}{3} u^{3/2} + 8 u^{1/2} + C = \dfrac{2}{5} (x + 3)^{5/2} - \dfrac{8}{3} (x + 3)^{3/2} + 8 (x + 3)^{1/2} + C.\quad\halmos$$

32. Compute $\displaystyle \int \dfrac{x - 3}{\sqrt{x^2 - 6 x + 5}}\,dx$ .

$$\int \dfrac{x - 3}{\sqrt{x^2 - 6 x + 5}}\,dx = \int \dfrac{x - 3}{\sqrt{u}} \cdot \dfrac{du}{2 (x - 3)} = \dfrac{1}{2} \int \dfrac{du}{\sqrt{u}} = \dfrac{1}{2} \cdot 2 \sqrt{u} + C = \sqrt{x^2 - 6 x + 5} + C.$$

$$\left[u = x^2 - 6 x + 5, \quad du = (2 x - 6)\,dx = 2(x - 3)\,dx, \quad dx = \dfrac{du}{2(x - 3)}\right]\quad\halmos$$

33. Compute $\displaystyle \int \dfrac{7}{e^{5 x}}\,dx$ .

$$\int \dfrac{7}{e^{5 x}}\,dx = \int 7 e^{-5 x}\,dx = -\dfrac{7}{5}e^{-5 x} + C.\quad\halmos$$

34. Compute $\displaystyle \int \dfrac{3}{\sec x}\,dx$ .

$$\int \dfrac{3}{\sec x}\,dx = \int 3 \cos x\,dx = 3 \sin x + C.\quad\halmos$$

35. Compute $\displaystyle \int \dfrac{5}{e^{4 x} + 7}\,dx$ .

$$\int \dfrac{5}{e^{4 x} + 7}\,dx = 5 \int \dfrac{1}{e^{4 x} + 7}\cdot \dfrac{e^{-4 x}}{e^{-4 x}}\,dx = 5 \int \dfrac{e^{-4 x}}{1 + 7 e^{-4 x}}\,dx = 5 \int \dfrac{e^{-4 x}}{u}\cdot \dfrac{du}{-28 e^{-4 x}} = -\dfrac{5}{28} \int \dfrac{du}{u} =$$

$$\left[u = 1 + 7 e^{-4 x}, \quad du = -28 e^{-4 x}\,dx, \quad dx = \dfrac{du}{-28 e^{-4 x}}\right]$$

$$-\dfrac{5}{28} \ln |u| + C = -\dfrac{5}{28} \ln |1 + 7 e^{-4 x}| + C.\quad\halmos$$

36. Compute $\displaystyle \int x e^{x^2} e^{(e^{x^2})}\,dx$ .

$$\int x e^{x^2} e^{(e^{x^2})}\,dx = \int x e^{x^2} e^u\cdot \dfrac{du}{2 x e^{x^2}} = \dfrac{1}{2} \int e^u\,du = \dfrac{1}{2} e^u + C = \dfrac{1}{2} e^{(e^{x^2})} + C.$$

$$\left[u = e^{x^2}, \quad du = 2 x e^{x^2}\,dx, \quad dx = \dfrac{du}{2 x e^{x^2}}\right] \quad\halmos$$

37. Compute $\displaystyle \int \left((\cos 7 x)^2 - (\sin 7 x)^2\right)\,dx$ .

$$\int \left((\cos 7 x)^2 - (\sin 7 x)^2\right)\,dx = \int \cos 14 x\,dx = \int \cos u \cdot \dfrac{du}{14} = \dfrac{1}{14} \int \cos u \,du = \dfrac{1}{14} \sin u + C = \dfrac{1}{14} \sin 14 x + C.$$

$$\left[u = 14 x, \quad du = 14\,dx, \quad dx = \dfrac{du}{14}\right]$$

In the first step, I used the double angle formula

$$(\cos \theta)^2 - (\sin \theta)^2 = \cos 2 \theta.\quad\halmos$$

38. Compute $\displaystyle \int \dfrac{\left(\sec \dfrac{1}{x^2}\right)^2}{x^3}\,dx$ .

$$\int \dfrac{\left(\sec \dfrac{1}{x^2}\right)^2}{x^3}\,dx = \int \dfrac{\left(\sec u\right)^2}{x^3}\cdot \left(-\dfrac{x^3}{2}\right) = -\dfrac{1}{2} \int (\sec u)^2\,du = -\dfrac{1}{2} \tan u + C = -\dfrac{1}{2} \tan \dfrac{1}{x^2} + C.$$

$$\left[u = \dfrac{1}{x^2}, \quad du = -\dfrac{2}{x^3}\,dx, \quad dx = -\dfrac{x^3}{2}\,du\right]\quad\halmos$$

39. Compute $\displaystyle \int (e^{3 x} - 2 e^{-x})(4 e^{5 x} + e^{3 x})\,dx$ .

I multiply the two terms out, using the rule $e^a e^b = e^{a + b}$ :

$$\int (e^{3 x} - 2 e^{-x})(4 e^{5 x} + e^{3 x})\,dx = \int (4 e^{8 x} + e^{6 x} - 8 e^{4 x} - 2 e^{2 x})\,dx = \dfrac{1}{2} e^{8 x} + \dfrac{1}{6} e^{6 x} - 2 e^{4 x} - e^{2 x} + C.\quad\halmos$$

40. Compute $\displaystyle \int \left(x\cos (x^2 + 4) - 5 x^2 \sin (x^3 + 2)\right)\,dx$ .

$$\int \left(x\cos (x^2 + 4) - 5 x^2 \sin (x^3 + 2)\right)\,dx = \int x \cos (x^2 + 4)\,dx - 5 \int x^2 \sin (x^3 + 2)\,dx =$$

$$\left[u = x^2 + 4, \quad du = 2 x\,dx, \quad dx = \dfrac{du}{2 x}; \quad w = x^3 + 2, \quad dw = 3 x^2\,dx, \quad dx = \dfrac{dw}{3 x^2}\right]$$

$$\int x \cos u \cdot \dfrac{du}{2 x} - 5 \int x^2 \sin w \cdot \dfrac{dw}{3 x^2} = \dfrac{1}{2} \int \cos u\,du - \dfrac{5}{3} \int \sin w\,dw =$$

$$\dfrac{1}{2} \sin u + \dfrac{5}{3} \cos w + C = \dfrac{1}{2} \sin (x^2 + 4) + \dfrac{5}{3} \cos (x^3 + 2) + C.\quad\halmos$$

41. Use a calculating device to approximate the following sum to at least three decimal places:

$$\dfrac{1}{3 + 1^2} + \dfrac{2}{3 + 2^2} + \dfrac{3}{3 + 3^2} + \cdots + \dfrac{47}{3 + 47^2}$$

$$\dfrac{1}{3 + 1^2} + \dfrac{2}{3 + 2^2} + \dfrac{3}{3 + 3^2} + \cdots + \dfrac{47}{3 + 47^2} = \sum_{n=1}^{47} \dfrac{n}{3 + n^2} = 3.28317 \ldots.\quad\halmos$$

42. Write the series in summation form:

(a) $\dfrac{2}{5} + \dfrac{3}{5^2} + \dfrac{4}{5^3} + \cdots + \dfrac{100}{5^{99}}$ .

(b) $\sqrt{3} \cdot \sin 4 + \sqrt{4} \cdot \sin 9 + \sqrt{5} \cdot \sin 16 + \cdots + \sqrt{100} \cdot \sin(99^2)$ .

(a)

$$\dfrac{2}{5} + \dfrac{3}{5^2} + \dfrac{4}{5^3} + \cdots + \dfrac{100}{5^{99}} = \sum_{n=1}^{99} \dfrac{n + 1}{5^n}.\quad\halmos$$

(b)

$$\sqrt{3} \cdot \sin 4 + \sqrt{4} \cdot \sin 9 + \sqrt{5} \cdot \sin 16 + \cdots + \sqrt{100} \cdot \sin(99^2) = \sum_{n=3}^{100} \sqrt{n} \cdot \sin (n - 1)^2.\quad\halmos$$

43. (a) Express the following sum in terms of n: $\displaystyle \sum_{k=1}^n (2 - 5 k + 7 k^2)$ .

(b) Find the exact value of $\displaystyle \sum_{n=1}^{1000} (n^2 + 5 n - 7)$ .

(a) Use the formulas

$$\eqalign{\sum_{k=1}^n c &= nc \cr \sum_{k=1}^n k &= \dfrac{n(n + 1)}{2} \cr \sum_{k=1}^n k^2 &= \dfrac{n(n + 1)(2 n + 1)}{6} \cr}.$$

Therefore,

$$\sum_{k=1}^n (2 - 5 k + 7 k^2) = \sum_{k=1}^n 2 - 5\sum_{k=1}^n k + 7\sum_{k=1}^n k^2 = 2 n - \dfrac{5 n (n + 1)}{2} + \dfrac{7 n (n + 1)(2 n + 1)}{6}.\quad\halmos$$

(b)

$$\sum_{n=1}^{1000} (n^2 + 5 n - 7) = \sum_{n=1}^{1000} n^2 + 5 \sum_{n=1}^{1000} n - \sum_{n=1}^{1000} 7 = \dfrac{(1000)(1001)(2001)}{6} + 5 \cdot \dfrac{(1000)(1001)}{2} - 7 \cdot 1000 = 336329000.\quad\halmos$$

44. (a) Verify that

$$\dfrac{1}{k^2 - k} = \dfrac{1}{k - 1} - \dfrac{1}{k}.$$

(b) Use the result of (a) to evaluate $\displaystyle \sum_{k=2}^{1000} \dfrac{1}{k^2 - k}$ .

(a) Adding the fractions on the right over a common denominator, I have

$$\dfrac{1}{k - 1} - \dfrac{1}{k} = \dfrac{1}{k - 1} \cdot \dfrac{k}{k} - \dfrac{1}{k} \cdot \dfrac{k - 1}{k - 1} = \dfrac{k}{k (k - 1)} - \dfrac{k - 1}{(k (k - 1)} =$$

$$\dfrac{k - (k - 1)}{k (k - 1)} = \dfrac{1}{k^2 - k}.\quad\halmos$$

(b)

$$\sum_{k=2}^{1000} \dfrac{1}{k^2 - k} = \sum_{k=2}^{1000} \left(\dfrac{1}{k - 1} - \dfrac{1}{k}\right) =$$

$$\left(\dfrac{1}{1} - \dfrac{1}{2}\right) + \left(\dfrac{1}{2} - \dfrac{1}{3}\right) + \left(\dfrac{1}{3} - \dfrac{1}{4}\right) + \cdots + \left(\dfrac{1}{999} - \dfrac{1}{1000}\right) = 1 - \dfrac{1}{1000} = \dfrac{999}{1000}.\quad\halmos$$

45. Approximate $\displaystyle \int_1^5 \dfrac{\sin x}{x}\,dx$ using 10 rectangles of equal width and using the left-hand endpoint of each subinterval to obtain the rectangles' heights.

The width of a rectangle is $\dfrac{5 - 1}{10} = 0.4$ . The left-hand endpoints are

$$1, \quad 1.4, \quad 1.8, \ldots 4.2, \quad 4.6.$$

To do the sum on a TI calculator, the calculator command is

sum(seq((sin(x))/x, x, 1, 4.6, 0.4)) * 0.4

The answer is $0.81579 \ldots$ .

46. Approximate $\displaystyle \int_1^5 \dfrac{\sin x}{x}\,dx$ using 10 rectangles of equal width and using the right-hand endpoint of each subinterval to obtain the rectangles' heights.

The width of a rectangle is $\dfrac{5 - 1}{10} = 0.4$ . The left-hand endpoints are

$$1.4, \quad 1.8, \quad 2.2, \ldots 4.2, \quad 4.6, \quad 5.$$

To do the sum on a TI calculator, the calculator command is

sum(seq((sin(x))/x, x, 1.4, 5, 0.4)) * 0.4

The answer is $0.40249 \ldots$ .

47. Approximate $\displaystyle \int_1^5 \dfrac{\sin x}{x}\,dx$ using 10 rectangles of equal width and using the midpoint of each subinterval to obtain the rectangles' heights.

The width of a rectangle is $\dfrac{5 - 1}{10} = 0.4$ . The midpoints are

$$1.2, \quad 1.6, \quad 2.0, \ldots 4.4, \quad 4.8.$$

To do the sum on a TI calculator, the calculator command is

sum(seq((sin(x))/x, x, 1.2, 4.8, 0.4)) * 0.4

The answer is $0.60119 \ldots$ .

48. Some values for a function $y = f(x)$ are shown below.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & x & & $f(x)$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 0 & & 1.00 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 0.2 & & 1.30 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 0.4 & & 1.58 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 0.6 & & 1.86 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 0.8 & & 2.14 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.0 & & 2.41 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.2 & & 2.68 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.4 & & 2.95 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.6 & & 3.21 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.8 & & 3.47 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 2.0 & & 3.73 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

(a) Approximate $\displaystyle \int_0^2 f(x)\,dx$ using 5 rectangles of equal width and using the left-hand endpoints to obtain the rectangle heights.

(b) Approximate $\displaystyle \int_0^2 f(x)\,dx$ using 10 rectangles of equal width and using the right-hand endpoints to obtain the rectangle heights.

(a) $\Delta x = \dfrac{2 - 0}{5} = 0.4$ , so the approximation is

$$(0.4)(1 + 1.58 + 2.14 + 2.68 + 3.21) = 4.244.\quad\halmos$$

(b) $\Delta x = \dfrac{2 - 0}{10} = 0.2$ , so the approximation is

$$(0.2)(1.30 + 1.58 + 1.86 + 2.14 + 2.41 + 2.68 + 2.95 + 3.21 + 3.47 + 3.73) = 5.06.\quad\halmos$$

49. Compute $\displaystyle \int_2^4 (2 x + 3)\,dx$ by writing the integral as the limit of a rectangle sum.

The width of a typical rectangle is

$$\Delta x = \dfrac{4 - 2}{n} = \dfrac{2}{n}.$$

I'll use the right-hand endpoints of the subintervals. (You could use the left-hand endpoints or the midpoints; the computation would look different, but the final answer would be the same.)

I'm going from 2 to 4 in steps of size $\dfrac{2}{n}$ . The diagram shows that right-hand endpoints:

$$\matrix{2 & 2 + \dfrac{2}{n} & 2 + \dfrac{4}{n} & 2 + \dfrac{6}{n} & \cdots & 2 + \dfrac{2(n-1)}{n} & 2 + \dfrac{2 n}{n} = 4 \cr \noalign{\vskip6 pt} & \uparrow & \uparrow & \uparrow & \cdots & \uparrow & \uparrow \cr}$$

The function is $f(x) = 2 x + 3$ . The rectangle sum is

$$\Delta x \left(f\left(2 + \dfrac{2}{n}\right) + f\left(2 + \dfrac{4}{n}\right) + f\left(2 + \dfrac{6}{n}\right) + \cdots + f\left(2 + \dfrac{2 n}{n}\right)\right) = \Delta x \sum_{i=1}^n f\left(2 + \dfrac{2 i}{n}\right) =$$

$$\dfrac{2}{n} \sum_{i=1}^n \left(2 \cdot \left(2 + \dfrac{2 i}{n}\right) + 3\right) = \dfrac{2}{n} \sum_{i=1}^n \left(\dfrac{4 i}{n} + 7\right) = \dfrac{8}{n^2} \sum_{i=1}^n i + \dfrac{2}{n} \sum_{i=1}^n 7 =$$

$$\dfrac{8}{n^2} \cdot \dfrac{n(n + 1)}{2} + \dfrac{2}{n} \cdot 7 n = \dfrac{4(n + 1)}{n} + 14.$$ Hence,

$$\int_2^4 (2 x + 3)\,dx = \lim_{n\to \infty} \left(\dfrac{4(n + 1)}{n} + 14\right) = 4 + 14 = 18.\quad\halmos$$

50. (a) Given that $\displaystyle \der {} x \dfrac{x^2 - 2 x + 5}{x^2 - 4 x + 5} = \dfrac{2(5 - x)^2}{(x^2 - 4 x + 5)^2}$ , what is $\displaystyle \int \dfrac{2(5 - x)^2}{(x^2 - 4 x + 5)^2}\,dx$ ?

(b) Compute $\displaystyle \int \left(\der {} x \sqrt{x^4 + x^2 + 1}\right)\,dx$ .

(a)

$$\int \dfrac{2(5 - x)^2}{(x^2 - 4 x + 5)^2}\,dx = \dfrac{x^2 - 2 x + 5}{x^2 - 4 x + 5} + C.\quad\halmos$$

(b)

$$\int \left(\der {} x \sqrt{x^4 + x^2 + 1}\right)\,dx = \sqrt{x^4 + x^2 + 1} + C.\quad\halmos$$

51. Compute $\displaystyle \int_{-1}^2 (x^2 + 1)^2\,dx$ .

$$\int_{-1}^2 (x^2 + 1)^2\,dx = \int_{-1}^2 (x^4 + 2 x^2 + 1)\,dx = \left[\dfrac{1}{5}x^5 + \dfrac{2}{3}x^3 + x\right]_{-1}^2 = \dfrac{78}{5}.\quad\halmos$$

52. Compute $\displaystyle \int_0^1 \dfrac{2 x^3 + x}{x^4 + x^2 + 3}\,dx$ .

$$\int_0^1 \dfrac{2 x^3 + x}{x^4 + x^2 + 3}\,dx = \int_3^5 \dfrac{2 x^3 + x}{u} \cdot \dfrac{du}{2(2 x^3 + x)} = \dfrac{1}{2} \int_3^5 \dfrac{1}{u}\,du = \dfrac{1}{2} \left[\ln |u|\right]_3^5 = \dfrac{1}{2} (\ln 5 - \ln 3).$$

$$\left[u = x^4 + x^2 + 3, \quad du = (4 x^3 + 2 x)\,dx = 2(2 x^3 + x)\,dx, \quad dx = \dfrac{du}{2(2 x^3 + x)}\right.$$

$$\left. \quad x = 0, u = 3; \quad x = 1, u = 5\right]\quad\halmos$$

53. Compute $\displaystyle \int_1^2 \dfrac{x + 2}{(x^2 + 4 x + 1)^2}\,dx$ .

$$\int_1^2 \dfrac{x + 2}{(x^2 + 4 x + 1)^2}\,dx = \int_6^{13} \dfrac{x + 2}{u^2} \cdot \dfrac{du}{2(x + 2)} = \dfrac{1}{2} \int_6^{13} \dfrac{1}{u^2}\,du = \dfrac{1}{2} \left[-\dfrac{1}{u}\right]_6^{13} = \dfrac{7}{156}.$$

$$\left[u = x^2 + 4 x + 1, \quad du = 2(x + 2)\,dx, \quad dx = \dfrac{du}{2(x + 2)}; \quad x = 1, \quad u = 6; \quad x = 2, \quad u = 13\right] \quad\halmos$$

54. Suppose that $f''(x) = 12 x + 6$ , $f'(0) = 3$ , and $f(1) = 5$ . Find $f(x)$ .

$$f'(x) = \int f''(x)\,dx = \int (12 x + 6)\,dx = 6 x^2 + 6 x + c.$$

Since $f'(0) = 3$ , I have

$$3 = f'(0) = 6 \cdot 0^2 + 6 \cdot 0 + c, \quad\hbox{or}\quad c = 3.$$

Thus, $f'(x) = 6 x^2 + 6 x + 3$ .

$$f(x) = \int f'(x)\,dx = \int (6 x^2 + 6 x + 3)\,dx = 2 x^3 + 3 x^2 + 3 x + d.$$

Since $f(1) = 5$ , I have

$$5 = f(1) = 2 \cdot 1^3 + 3 \cdot 1^2 + 3 \cdot 1 + d, \quad\hbox{or}\quad d = -3.$$

Therefore, $f(x) = 2 x^3 + 3 x^2 + 3 x - 3$ .

55. Find functions $f(x)$ and $g(x)$ such that the antiderivative of $f(x) \cdot g(x)$ is not equal to the antiderivative of $f(x)$ times the antiderivative of $g(x)$ .

There are lots of possibilities. For example, take $f(x) = 1$ and $g(x) = x$ . Then

$$\int f(x) g(x)\,dx = \int 1\cdot x\,dx = \dfrac{1}{2} x^2 + C.$$

But

$$\int f(x)\,dx = \int 1\,dx = x + C \quad\hbox{and}\quad \int g(x)\,dx = \int x\,dx = \dfrac{1}{2} x^2 + C.$$

Obviously, $\dfrac{1}{2} x^2 \ne x \cdot \dfrac{1}{2}x^2$ .

56. Compute $\displaystyle \int_{-1}^1 (1 - |x|)\,dx$ .

Here is the graph of $y = 1 - |x|$ .

$$\hbox{\epsfysize=1.75in \epsffile{rev3-8.eps}}$$

$\int_{-1}^1 (1 - |x|)\,dx$ is the area under the graph and above the x-axis, from $x = -1$ to $x = 1$ . This is the shaded region in the picture. It is a triangle with height 1 and base 2, so its area is

$$\int_{-1}^1 (1 - |x|)\,dx = \dfrac{1}{2} \cdot 2 \cdot 1 = 1.\quad\halmos$$

57. Compute the exact value of $\displaystyle \int_{-10}^{10} (5 + \sqrt{100 - x^2})\,dx$ .

First, break the integral up into two pieces:

$$\int_{-10}^{10} (5 + \sqrt{100 - x^2})\,dx = \int_{-10}^{10} 5\,dx + \int_{-10}^{10} \sqrt{100 - x^2}\,dx.$$

The first integral can be computed directly:

$$\int_{-10}^{10} 5\,dx = 5 [10 - (-10)] = 100.$$

For the second integral, notice that $y = \sqrt{100 - x^2}$ is a semicircle:

$$\eqalign{ y & = \sqrt{100 - x^2} \cr y^2 & = 100 - x^2 \cr x^2 + y^2 & = 100 \cr}$$

The radius is $\sqrt{100} = 10$ , and it's centered at the origin.

$$\hbox{\epsfysize=1.5in \epsffile{rev3-9.eps}}$$

The integral is computing the area of the semicircle, which is half the area of a circle of radius 10:

$$\int_{-10}^{10} \sqrt{100 - x^2}\,dx = \dfrac{1}{2} \pi 10^2 = 50 \pi.$$

Therefore,

$$\int_{-10}^{10} (5 + \sqrt{100 - x^2})\,dx = 100 + 50 \pi.\quad\halmos$$

58. Compute the exact value of $\displaystyle \int_{-1}^7 \sqrt{7 + 6 x - x^2}\,dx$ .

Hint: Complete the square in x.

You can't compute this integral directly using techniques you know now.

If $y = \sqrt{7 + 6 x - x^2}$ , then

$$y^2 = 7 + 6 x - x^2, \quad x^2 - 6 x + y^2 = 7, \quad x^2 - 6 x + 9 + y^2 = 7 + 9, \quad (x - 3)^2 + y^2 = 16.$$

(I knew to add 9 to both sides, since $\dfrac{1}{2}(-6) = -3$ , then $(-3)^2 = 9$ . You should have seen this when you took algebra; it's called completing the square.)

The equation represents a circle of radius $\sqrt{16} = 4$ centered at $(3,0)$ . If I go 4 units to the left and right of $x = 3$ , I get $x = -1$ , and $x = 7$ , which are the limits on the integral. Finally, $y = \sqrt{7 + 6 x - x^2}$ represents the top semicircle of the circle, because $\sqrt{}$ always gives the positive square root.

$$\hbox{\epsfysize=1.5in \epsffile{rev3-10.eps}}$$

Putting everything together, I see that the integral represents the area of a semicircle of radius 4. Since the area of a circle of radius r is $\pi r^2$ ,

$$\int_{-1}^7 \sqrt{7 + 6 x - x^2}\,dx = \dfrac{1}{2} \pi \cdot 4^2 = 8 \pi.\quad\halmos$$

59. Find the total area of the region bounded by $y = x(x - 2)(x - 4)$ and the x-axis.

$$\hbox{\epsfysize=1.75in \epsffile{rev3-11.eps}}$$

The curve is positive from 0 to 2 and negative from 2 to 4, so the area is

$$\int_0^2 x(x - 2)(x - 4)\,dx + \int_2^4 -x(x - 2)(x - 4)\,dx.$$

$x(x - 2)(x - 4) = x^3 - 6 x^2 + 8 x$ , so

$$\int x(x - 2)(x - 4) = \int(x^3 - 6 x^2 + 8 x)\,dx = \dfrac{1}{4}x^4 - 2 x^3 + 4 x^2 + C.$$

Using this in the integrals above, I find that the area is

$$\int_0^2 x(x - 2)(x - 4)\,dx + \int_2^4 -x(x - 2)(x - 4)\,dx = 8.\quad\halmos$$

60. Find the area of the region bounded by

$$x = y^2 - 9 \quad\hbox{and}\quad x = 2 y + 6.$$

$x = y^2 - 9$ is a parabola opening to the right, and $x = 2 y + 6$ is a line.

$$\hbox{\epsfysize=1.5in \epsffile{rev3-12.eps}}$$

Find the intersections:

$$\eqalign{ y^2 - 9 & = 2 y + 6 \cr y^2 - 2 y - 15 & = 0 \cr (y - 5)(y + 3) & = 0 \cr}$$

The curves intersect at $y = 5$ and $y = -3$ .

Use horizontal rectangles. The right end of a horizontal rectangle is on $x = 2 y + 6$ and the left end is on $x = y^2 - 9$ . So the area is

$$\int_{-3}^5 [(2 y + 6) - (y^2 - 9)]\,dy = \int_{-3}^5 (15 + 2 y - y^2)\,dy = \left[15 y + y^2 - \dfrac{1}{3} y^3\right]_{-3}^5 = \dfrac{256}{3}.\quad\halmos$$

61. Find the area of the region in the first quadrant bounded on the left by $y = 1 - x^2$ , on the right by $y = 1 - \dfrac{x^2}{2}$ , and below by the x-axis.

$$\hbox{\epsfysize=1.75in \epsffile{rev3-13.eps}}$$

I'll find the area using horizontal rectangles; vertical rectangles would require two integrals.

The left-hand curve is

$$y = 1 - x^2 \quad\hbox{or}\quad x = \sqrt{1 - y}.$$

The right-hand curve is

$$y = 1 - \dfrac{x^2}{2} \quad\hbox{or}\quad x = \sqrt{2}\sqrt{1 - y}.$$

The region extends from $y = 0$ to $y = 1$ . The area is

$$\int_0^1 \left(\sqrt{2}\sqrt{1 - y} - \sqrt{1 - y}\right)\,dy = (\sqrt{2} - 1) \int_0^1 \sqrt{1 - y}\,dy = \dfrac{2}{3} (\sqrt{2} - 1) = 0.27614 \ldots.\quad\halmos$$

62. Find the area of the region bounded by the graphs of $y = 1 - x^2$ and $y = -1 - x$ .

$$\hbox{\epsfysize=1.75in \epsffile{rev3-14.eps}}$$

Solve simultaneously:

$$1 - x^2 = -1 - x, \quad x^2 - x - 2 = 0, \quad (x - 2)(x + 1) = 0, \quad x = -1 \quad\hbox{or}\quad x = 2.$$

The top curve is $y = 1 - x^2$ and the bottom curve is $y = -1 - x$ . The area is

$$\int_{-1}^2 \left((1 - x^2) - (-1 - x)\right)\,dx = \dfrac{9}{2} = 4.5.\quad\halmos$$

63. Find the area of the region between $y = -x^2$ and $y = x - 6$ , from $x = 0$ to $x = 3$ .

Find the intersection points:

$$-x^2 = x - 6, \quad x^2 + x - 6 = 0, \quad (x - 2)(x + 3) = 0, \quad x = 2 \quad\hbox{or}\quad x = -3.$$

On the interval $0 \le x \le 3$ , the curves cross at $x = 2$ .

$$\hbox{\epsfysize=1.5in \epsffile{rev3-15.eps}}$$

I need two integrals to find the area. From $x = 0$ to $x = 2$ , the top curve is $y = -x^2$ and the bottom curve is $y = x - 6$ . From $x = 2$ to $x = 3$ , the top curve is $y = x - 6$ and the bottom curve is $y = -x^2$ . The area is

$$\int_0^2 \left(-x^2 - (x - 6)\right)\,dx + \int_2^3 \left((x - 6) - (-x^2)\right)\,dx = \int_0^2 \left(-x^2 - x + 6\right)\,dx + \int_2^3 \left(x - 6 + x^2)\right)\,dx =$$

$$\left[-\dfrac{1}{3} x^3 - \dfrac{1}{2} x^2 + 6 x\right]_0^2 + \left[\dfrac{1}{2} x^2 - 6 x + \dfrac{1}{3} x^3\right]_2^3 = \dfrac{61}{6}.\quad\halmos$$

64. (a) Compute $\displaystyle \der {} x \int_{-17}^x \dfrac{\cos t}{t^4 + 1}\,dt$ .

(b) Compute $\displaystyle \der {} x \int_{42}^{\sin x} \sqrt{t^2 + 2}\,dt$ .

(c) Compute $\displaystyle \der {} x \int_{e^x}^{13} \dfrac{t}{2 + \sin t}\,dt$ .

(a) Using the second form of the Fundamental Theorem of Calculus, I get

$$\der {} x \int_{-17}^x \dfrac{\cos t}{t^4 + 1}\,dt = \dfrac{\cos x}{x^4 + 1}.\quad\halmos$$

(b) In this situation, I'm differentiating with respect to x, but the top limit in the integral is $\sin x$ --- they don't match. In order to apply the second form of the Fundamental Theorem, I need to use the Chain Rule to "make them match":

$$\der {} x \int_{42}^{\sin x} \sqrt{t^2 + 2}\,dt = \left(\dfrac{d(\sin x)}{dx}\right)\cdot \dfrac{d}{d(\sin x)} \int_{42}^{\sin x} \sqrt{t^2 + 2}\,dt = (\cos x)\sqrt{(\sin x)^2 + 2}.\quad\halmos$$

(c)

$$\der {} x \int_{e^x}^{13} \dfrac{t}{2 + \sin t}\,dt = -\der {} x \int_{13}^{e^x} \dfrac{t}{2 + \sin t}\,dt = -\dfrac{d e^x}{dx} \dfrac{d}{d(e^x)} \int_{13}^{e^x} \dfrac{t}{2 + \sin t}\,dt = -e^x \cdot \dfrac{e^x}{2 + \sin e^x}.\quad\halmos$$

65. (a) Prove that $\displaystyle \int_0^{0.5} \dfrac{x^2}{x^2 + 1}\,dx \le 0.5$ .

(b) Use the Integral Mean Value Theorem to estimate $\displaystyle \int_0^1 e^{x^4}\,dx$ .

(a) Since $x^2 + 1 \ge x^2$ , it follows that $1 \ge \dfrac{x^2}{x^2 + 1}$ . Hence,

$$\int_0^{0.5} 1\,dx \ge \int_0^{0.5} \dfrac{x^2}{x^2 + 1}\,dx, \quad\hbox{or}\quad 0.5 \ge \int_0^{0.5} \dfrac{x^2}{x^2 + 1}\,dx.\quad\halmos$$

(b) If $f(x) = e^{x^4}$ , then $f'(x) = 4 x^3 e^{x^4}$ . Note that $f'(x) = 0$ for $x = 0$ , and $f'(x)$ is defined for all x.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & x & & 0 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $f(x)$ & & 1 & & e & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The maximum value of $f(x)$ on $0 \le x \le 1$ is e and the minimum value is 1. Thus, $1 \le e^{x^4} \le e$ .

The Integral Mean Value Theorem says that for some c satisfying $0 \le c \le 1$ ,

$$\int_0^1 e^{x^4}\,dx = (1 - 0)f(c) = e^{c^4}.$$

The max-min result I derived above shows that $1 \le e^{c^4} \le e$ . Hence,

$$1 \le \int_0^1 e^{x^4}\,dx \le e.\quad\halmos$$

You are all you will ever have for certain. - June Havoc

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga