Review Problems for Test 1

Math 211

These problems are provided to help you study. The presence of a problem on this sheet does not imply that a similar problem will appear on the test. And the absence of a problem from this sheet does not imply that the test will not have a similar problem.

1. Compute $\displaystyle \int x^3 e^{4 x}\,dx$ .

2. Compute $\displaystyle \int e^{4 x} \cos 2 x\,dx$ .

3. Compute $\displaystyle \int (x^2 + x + 1) \cos x\,dx$ .

4. Compute $\displaystyle \int \cos 3 x \sin 2 x\,dx$ .

5. Compute $\displaystyle \int \ln (x^2 + 5)\,dx$ .

6. Compute $\displaystyle \int_0^{\pi/2} (\cos x)^3\left(1 + (\sin x)^{1/2}\right)\,dx$ .

7. Compute $\displaystyle \int (\cos 7 x)^4\,dx$ .

8. Compute $\displaystyle \int [\sin (x + 3)]^2[\cos (x + 3)]^2\,dx$ .

9. Compute $\displaystyle \int (\sec 3 x)^5 \tan 3 x\,dx$ .

10. Compute $\displaystyle \int (\tan x)^4\,dx$ .

11. Compute $\displaystyle \int (\csc 2 x)^3(\cot 2 x)^3\,dx$ .

12. Compute $\displaystyle \int \sqrt{x^2 - 1}\,dx$ .

13. Compute $\displaystyle \int x^2 \sqrt{25 - x^2}\,dx$ .

14. Compute $\displaystyle \int x \sqrt{25 - x^2}\,dx$ .

15. Compute $\displaystyle \int \dfrac{x^2}{(x^2 - 9)^{3/2}}\,dx$ .

16. Compute $\displaystyle \int \dfrac{x^2}{\sqrt{x^2 + 1}}\,dx$ .

17. Compute $\displaystyle \int \dfrac{-x + 18}{x^2 - 8 x + 12}\,dx$ .

18. Compute $\displaystyle \int \dfrac{-3 x^2 + 47 x - 150}{(x - 6)^2 (x + 2)}\,dx$ .

19. Compute $\displaystyle \int \dfrac{3 + 4 x + 5 x^2 + 3 x^3}{x^2(x + 3)}\,dx$ .

20. Compute $\displaystyle \int \dfrac{1}{x^{1/2}(x^{1/3} + x^{1/4})}\,dx$ .

21. Compute $\displaystyle \int \dfrac{1}{x^{7/8} + x^{5/8}}\,dx$ .

22. Compute $\displaystyle \int \dfrac{1}{\sqrt{7 + 6 x - x^2}}\,dx$ .

23. Compute $\displaystyle \int \dfrac{1}{x^2 + 10 x + 74}\,dx$ .

24. Compute $\displaystyle \int \dfrac{x - 2}{x^2 - 8 x + 25}\,dx$ .

25. Compute $\displaystyle \int \dfrac{x + 3}{\sqrt{-x^2 - 6 x - 8}}\,dx$ .

26. Compute $\displaystyle \int \dfrac{1}{2 x^2 + 8 x + 10}\,dx$ .

27. Compute $\displaystyle \int \dfrac{6 x^3 - 24 x^2 + 16 x + 4}{x^4 - 4 x^3 + 4 x^2}\,dx$ .

28. Compute $\displaystyle \int \dfrac{4 x^3 + 2 x^2 + 16 x + 11}{(x^2 + 1)(x^2 + 4)}\,dx$ .

29. Compute $\displaystyle \int \dfrac{2 x^2 - 9 x + 11}{(x - 1)^3}\,dx$ .

30. How would you try to decompose $\dfrac{2(x - 2)^2}{x^4(x^2 + 4)^3}$ using partial fractions? (Just write out the fractions --- you don't need to solve for the parameters.)

31. What is wrong with the following "partial fractions decomposition"?

$$\dfrac{5 x}{(x - 1)^2(x + 1)} = \dfrac{A}{(x - 1)^2} + \dfrac{B}{x + 1}?$$

32. What is wrong with the following "partial fractions decomposition"?

$$\dfrac{7}{x(x - 1)} = \dfrac{A}{x} + \dfrac{B}{x} + \dfrac{C}{x - 1}.$$

33. Find the partial fractions decomposition of

$$\dfrac{-3 x^4 + x^3 - 6 x^2 - 3}{x(x^2 + 1)^2}.$$

34. (a) Compute $\displaystyle \int \dfrac{-x^2 + 8 x - 4}{x(x^2 + x - 2)}\,dx$ .

(b) Calvin Butterball tries to use the antiderivative from (a) to compute

$$\int_{-1}^{1/2} \dfrac{-x^2 + 8 x - 4}{x(x^2 + x - 2)}\,dx.$$

He gets

$$\left[2 \ln |x| + \ln |x - 1| - 4\ln |x + 2|\right]_{-1}^{1/2} = \left(2\ln \dfrac{1}{2} + \ln \dfrac{1}{2} - 4\ln {3}{2}\right) - (2\ln 1 + \ln 2 - 4\ln 1) \approx -4.39445.$$

Does this computation make sense? Why or why not?

35. Find the area of the region under $y = \dfrac{x}{(x^2 + 1)^2}$ from $x = 0$ to $\infty$ .

36. Compute $\displaystyle \int_4^6 \dfrac{1}{\sqrt{x - 4}}\,dx$ .

37. Compute $\displaystyle \int_{-\infty}^0 x e^{x^2}\,dx$ .

38. Compute $\displaystyle \int_0^\infty x e^{-3 x}\,dx$ .

39. Compute $\displaystyle \int_0^\infty \cos 3 x\,dx$ .

40. Compute $\displaystyle \int_1^\infty \dfrac{x^2 + 4}{x^3 + 12 x + 1}\,dx$ .

41. Compute $\displaystyle \int_1^\infty \dfrac{x^2 + 4}{(x^3 + 12 x + 1)^2}\,dx$ .

42. Compute $\displaystyle \int_2^{11} \dfrac{1}{{\root 3 \of {x - 3}}}\,dx$ .

43. Prove that $\displaystyle \int_0^\infty e^{-x^4}\,dx$ converges. [Hint: Compare the integral to $\displaystyle \int_0^\infty e^{-x}\,dx$ .]

44. Prove that $\displaystyle \int_0^\infty \dfrac{(\sin x)^2}{x^2 + 1}\,dx$ converges. [Hint: Use comparison, starting with the fact that $(\sin x)^2 \le 1$ .]

45. (a) Show that the following integrals both diverge:

$$\int_0^\infty x\,dx \quad\hbox{and}\quad \int_{-\infty}^0 x\,dx.$$

(It follows that $\displaystyle \int_{-\infty}^\infty x\,dx$ diverges as well.)

(b) Show that $\displaystyle \lim_{b \to \infty} \int_{-b}^b x\,dx$ converges. (This is called the Cauchy principal value of the integral; this problem shows that $\displaystyle \lim_{b \to \infty} \int_{-b}^b x\,dx$ is not the same as $\displaystyle \int_{-\infty}^\infty x\,dx$ .)

Solutions to the Review Problems for Test 1

1. Compute $\displaystyle \int x^3 e^{4 x}\,dx$ .

$$\matrix{& \der {} x & & \displaystyle \int\,dx \cr & & & \cr + & x^3 & & e^{4 x} \cr & & \searrow & \cr - & 3 x^2 & & \dfrac{1}{4}e^{4 x} \cr & & \searrow & \cr + & 6 x & & \dfrac{1}{16}e^{4 x} \cr & & \searrow & \cr - & 6 & & \dfrac{1}{64}e^{4 x} \cr & & \searrow & \cr + & 0 & & \dfrac{1}{256}e^{4 x} \cr}$$

$$\int x^3 e^{4 x}\,dx = \dfrac{1}{4}x^3e^{4 x} - \dfrac{3}{16}x^2e^{4 x} + \dfrac{6}{64} xe^{4 x} - \dfrac{6}{256}e^{4 x} + C.\quad\halmos$$

2. Compute $\displaystyle \int (x^2 + x + 1) \cos x\,dx$ .

$$\matrix{ & \displaystyle \der {} x & \displaystyle \int\,dx \cr \noalign{\vskip2pt} + & x^2 + x + 1 & \cos x \cr \noalign{\vskip2pt} - & 2 x + 1 & \sin x \cr \noalign{\vskip2pt} + & 2 & -\cos x \cr \noalign{\vskip2pt} - & 0 & -\sin x \cr}$$

$$\int (x^2 + x + 1) \cos x\,dx = (x^2 + x + 1) \sin x + (2 x + 1) \cos x - 2 \sin x + C.\quad\halmos$$

3. Compute $\displaystyle \int e^{4 x} \cos 2 x\,dx$ .

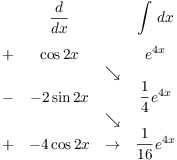
$$\matrix{& \der {} x & & \displaystyle \int\,dx \cr & & & \cr + & \cos 2 x & & e^{4 x} \cr & & \searrow & \cr - & -2\sin 2 x & & \dfrac{1}{4}e^{4 x} \cr & & \searrow & \cr + & -4\cos 2 x & \to & \dfrac{1}{16}e^{4 x} \cr}$$

$$\int e^{4 x} \cos 2 x\,dx = \dfrac{1}{4}e^{4 x} \cos 2 x + \dfrac{1}{8}e^{4 x} \sin 2 x - \dfrac{1}{4} \int e^{4 x} \cos 2 x\,dx,$$

$$\int e^{4 x} \cos 2 x\,dx + \dfrac{1}{4} \int e^{4 x} \cos 2 x\,dx = \dfrac{1}{4}e^{4 x} \cos 2 x + \dfrac{1}{8}e^{4 x} \sin 2 x - \dfrac{1}{4} \int e^{4 x} \cos 2 x\,dx + \dfrac{1}{4} \int e^{4 x} \cos 2 x\,dx,$$

$$\dfrac{5}{4} \int e^{4 x} \cos 2 x\,dx = \dfrac{1}{4}e^{4 x} \cos 2 x + \dfrac{1}{8}e^{4 x} \sin 2 x,$$

$$\dfrac{4}{5} \cdot \dfrac{5}{4} \int e^{4 x} \cos 2 x\,dx = \dfrac{4}{5} \cdot \dfrac{1}{4}e^{4 x} \cos 2 x + \dfrac{4}{5} \cdot \dfrac{1}{8}e^{4 x} \sin 2 x,$$

$$\int e^{4 x} \cos 2 x\,dx = \dfrac{1}{5}e^{4 x} \cos 2 x + \dfrac{1}{10}e^{4 x} \sin 2 x + C. \quad\halmos$$

4. Compute $\displaystyle \int \cos 3 x \sin 2 x\,dx$ .

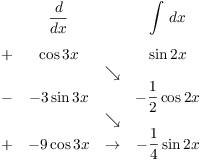
$$\matrix{& \der {} x & & \displaystyle \int\,dx \cr & & & \cr + & \cos 3 x & & \sin 2 x \cr & & \searrow & \cr - & -3\sin 3 x & & -\dfrac{1}{2}\cos 2 x \cr & & \searrow & \cr + & -9\cos 3 x & \to & -\dfrac{1}{4}\sin 2 x \cr}$$

$$\int \cos 3 x \sin 2 x\,dx = -\dfrac{1}{2} \cos 3 x \cos 2 x - \dfrac{3}{4} \sin 3 x \sin 2 x + \dfrac{9}{4}\int \cos 3 x \sin 2 x\,dx,$$

$$-\dfrac{5}{4}\int \cos 3 x \sin 2 x\,dx = -\dfrac{1}{2} \cos 3 x \cos 2 x - \dfrac{3}{4} \sin 3 x \sin 2 x,$$

$$\int \cos 3 x \sin 2 x\,dx = \dfrac{2}{5} \cos 3 x \cos 2 x + \dfrac{3}{5} \sin 3 x \sin 2 x + C. \quad\halmos$$

5. Compute $\displaystyle \int \ln (x^2 + 5)\,dx$ .

$$\matrix{& \der {} x & & \displaystyle \int\,dx \cr & & & \cr + & \ln (x^2 + 5) & & 1 \cr & & \searrow & \cr - & \dfrac{2 x}{x^2 + 5} & & x \cr}$$

$$\int \ln (x^2 + 5)\,dx = x \ln (x^2 + 5) - \int \dfrac{2 x^2}{x^2 + 5}\,dx = x \ln (x^2 + 5) - \int \left(2 - \dfrac{10}{x^2 + 5}\right)\,dx =$$

$$x \ln (x^2 + 5) - 2 x + \dfrac{10}{\sqrt{5}} \tan^{-1} \dfrac{x}{\sqrt{5}} + C.$$

The second equality comes from dividing $2 x^2$ by $x^2 + 5$ (long division). Alternatively, you can do this:

$$\dfrac{2 x^2}{x^2 + 5} = \dfrac{2 x^2 + 10 - 10}{x^2 + 5} = \dfrac{2 x^2 + 10}{x^2 + 5} - \dfrac{10}{x^2 + 5} = \dfrac{2(x^2 + 5)}{x^2 + 5} - \dfrac{10}{x^2 + 5} = 2 - \dfrac{10}{x^2 + 5}.\quad\halmos$$

6. Compute $\displaystyle \int_0^{\pi/2} (\cos x)^3\left(1 + (\sin x)^{1/2}\right)\,dx$ .

I'll do the antiderivative first:

$$\int (\cos x)^3 \left(1 + (\sin x)^{1/2}\right)\,dx = \int (\cos x)^2 \left(1 + (\sin x)^{1/2}\right) \cos x\,dx =$$

$$\int \left(1 - (\sin x)^2\right) \left(1 + (\sin x)^{1/2}\right) \cos x\,dx =$$

$$\left[u = \sin x, \quad du = \cos x\,dx, \quad dx = \dfrac{du}{\cos x}\right]$$

$$\int (1 - u^2)(1 + u^{1/2})\,du = \int (1 + u^{1/2} - u^2 - u^{5/2})\,du = u + \dfrac{2}{3} u^{3/2} - \dfrac{1}{3} u^3 - \dfrac{2}{7} u^{7/2} + C =$$

$$\sin x + \dfrac{2}{3}(\sin x)^{3/2} - \dfrac{1}{3}(\sin x)^3 - \dfrac{2}{7}(\sin x)^{7/2} + C.$$

Therefore,

$$\int_0^{\pi/2} (\cos x)^3\left(1 + (\sin x)^{1/2}\right)\,dx = \left[\sin x + \dfrac{2}{3}(\sin x)^{3/2} - \dfrac{1}{3}(\sin x)^3 - \dfrac{2}{7}(\sin x)^{7/2}\right]_0^{\pi/2} = \dfrac{22}{21}.\quad\halmos$$

7. Compute $\displaystyle \int (\cos 7 x)^4\,dx$ .

$$\int (\cos 7 x)^4\,dx = \int (\cos 7 x)^2(\cos 7 x)^2\,dx = \int \dfrac{1}{2}(1 + \cos 14 x)\cdot \dfrac{1}{2}(1 + \cos 14 x)\,dx =$$

$$\dfrac{1}{4} \int \left(1 + 2\cos 14 x + (\cos 14 x)^2\right)\,dx = \dfrac{1}{4} \int \left(1 + 2\cos 14 x + \dfrac{1}{2}(1 + \cos 28 x)\right)\,dx =$$

$$\dfrac{1}{4} \left(x + \dfrac{1}{7}\sin 14 x + \dfrac{1}{2}(x + \dfrac{1}{28}\sin 28 x)\right) + C.\quad\halmos$$

8. Compute $\displaystyle \int [\sin (x + 3)]^2[\cos (x + 3)]^2\,dx$ .

$$\int [\sin (x + 3)]^2[\cos (x + 3)]^2\,dx = \int \left(\dfrac{1}{2} [1 - \cos 2(x + 3)]\right) \left(\dfrac{1}{2} [1 + \cos 2(x + 3)]\right)\,dx =$$

$$\dfrac{1}{4} \int \left(1 - [\cos 2(x + 3)]^2\right)\,dx = \dfrac{1}{4} \int [\sin 2(x + 3)]^2\,dx = \dfrac{1}{4} \int \dfrac{1}{2}[1 - \cos 4(x + 3)]\,dx =$$

$$\dfrac{1}{8}\left(x - \dfrac{1}{4} \sin 4(x + 3)\right) + C.\quad\halmos$$

9. Compute $\displaystyle \int (\sec 3 x)^5 \tan 3 x\,dx$ .

$$\int (\sec 3 x)^5 \tan 3 x\,dx = \int (\sec 3 x)^4 (\sec 3 x \tan 3 x\,dx) = \dfrac{1}{3} \int u^4\,du = \dfrac{1}{15} u^5 + C = \dfrac{1}{15} (\sec 3 x)^5 + C.$$

$$\left[u = \sec 3 x, \quad du = 3\sec 3 x \tan 3 x\,dx, \quad dx = \dfrac{du}{3\sec 3 x \tan 3 x}\right]\quad\halmos$$

10. Compute $\displaystyle \int (\tan x)^4\,dx$ .

$$\int (\tan x)^4\,dx = \int (\tan x)^2 (\tan x)^2\,dx = \int (\tan x)^2 \left((\sec x)^2 - 1\right)\,dx =$$

$$\int (\tan x)^2 (\sec x)^2\,dx - \int (\tan x)^2\,dx = \int (\tan x)^2 (\sec x)^2\,dx - \int \left((\sec x)^2 - 1\right)\,dx =$$

$$\int (\tan x)^2 (\sec x)^2\,dx - \int (\sec x)^2\,dx + \int\,dx =$$

$$\left[u = \tan x, \quad du = (\sec x)^2\,dx, \quad dx = \dfrac{du}{(\sec x)^2}\right]$$

$$\int u^2\,du - \tan x + x + C = \dfrac{1}{3}u^3 - \tan x + x + C = \dfrac{1}{3}(\tan x)^3 - \tan x + x + C.\quad\halmos$$

11. Compute $\displaystyle \int (\csc 2 x)^3(\cot 2 x)^3\,dx$ .

$$\int (\csc 2 x)^3(\cot 2 x)^3\,dx = \int (\csc 2 x)^2(\cot 2 x)^2(\csc 2 x \cot 2 x)\,dx =$$

$$\int (\csc 2 x)^2\left[(\csc 2 x)^2 - 1\right] (\csc 2 x \cot 2 x)\,dx = \int u^2(u^2 - 1)(\csc 2 x \cot 2 x)\cdot \dfrac{du}{-2\csc 2 x \cot 2 x} =$$

$$\left[u = \csc 2 x, \quad du = -2\csc 2 x \cot 2 x\,dx, \quad dx = \dfrac{du}{-2\csc 2 x \cot 2 x}\right]$$

$$-\dfrac{1}{2} \int u^2(u^2 - 1)\,du = -\dfrac{1}{2} \int (u^4 - u^2)\,du = -\dfrac{1}{2} \left(\dfrac{1}{5}u^5 - \dfrac{1}{3}u^3\right) + C = -\dfrac{1}{2} \left(\dfrac{1}{5}(\csc 2 x)^5 - \dfrac{1}{3}(\csc 2 x)^3\right) + C.\quad\halmos$$

12. Compute $\displaystyle \int \sqrt{x^2 - 1}\,dx$ .

$$\int \sqrt{x^2 - 1}\,dx = \int \sqrt{(\sec \theta)^2 - 1} \sec \theta \tan \theta\,d\theta = \int \sqrt{(\tan \theta)^2} \sec \theta \tan \theta\,d\theta = \int \sec \theta(\tan \theta)^2\,d\theta =$$

$$\hfil\raise0.5in\hbox{$\left[x = \sec \theta, \quad dx = \sec \theta \tan \theta\,d\theta\right]$} \hskip0.5in \hbox{\epsfysize=1in \epsffile{rev1-7.eps}}\hfil$$

$$\int \sec \theta\left((\sec \theta)^2 - 1\right)\,d\theta = \int \left((\sec \theta)^3 - \sec \theta\right)\,d\theta = \dfrac{1}{2} \sec \theta \tan \theta + \dfrac{1}{2} \ln |\sec \theta + \tan \theta| - \ln |\sec \theta+ \tan \theta| + C =$$

$$\dfrac{1}{2} \sec \theta \tan \theta - \dfrac{1}{2} \ln |\sec \theta + \tan \theta| + C = \dfrac{1}{2} x\sqrt{x^2 - 1} - \dfrac{1}{2}\ln |x + \sqrt{x^2 - 1}| + C.\quad\halmos$$

13. Compute $\displaystyle \int x^2 \sqrt{25 - x^2}\,dx$ .

$$\int x^2 \sqrt{25 - x^2}\,dx = \int 25 (\sin \theta)^2 \sqrt{25 - 25(\sin \theta)^2} (5 \cos \theta)\,d\theta = \int 25 (\sin \theta)^2 \sqrt{25(\cos \theta)^2} (5 \cos \theta)\,d\theta =$$

$$\hfil\raise0.5in\hbox{$\left[x = 5 \sin \theta, \quad dx = 5 \cos \theta\,d\theta\right]$} \hskip0.5in \hbox{\epsfysize=1in \epsffile{rev1-8.eps}}\hfil$$

$$625 \int (\sin \theta)^2(\cos \theta)^2\,d\theta = 625 \int \dfrac{1}{2}(1 - \cos 2\theta)\cdot \dfrac{1}{2}(1 + \cos 2\theta)\,d\theta = \dfrac{625}{4} \int \left(1 - (\cos 2\theta)^2\right)\,d\theta =$$

$$\dfrac{625}{4} \int (\sin 2\theta)^2\,d\theta = \dfrac{625}{4} \int \dfrac{1}{2}(1 - \cos 4\theta)\,d\theta = \dfrac{625}{8}(\theta- \dfrac{1}{4} \sin 4\theta) + C =$$

$$\dfrac{625}{8}\left(\theta - \sin \theta \cos \theta\left(2(\cos \theta)^2 - 1\right)\right) + C = \dfrac{625}{8}\arcsin \dfrac{x}{5} - \dfrac{1}{8}x\left(\sqrt{25 - x^2}\right)(25 - 2 x^2) + C.\quad\halmos$$

14. Compute $\displaystyle \int x\sqrt{25 - x^2}\,dx$ .

$$\int x\sqrt{25 - x^2}\,dx = \int x\sqrt{u}\cdot \left(\dfrac{du}{-2 x}\right) = -\dfrac{1}{2} \int u^{1/2}\,du = -\dfrac{1}{3} u^{3/2} + C = -\dfrac{1}{3}(25 - x^2)^{3/2} + C.$$

$$\left[u = 25 - x^2, \quad du = -2 x\,dx, \quad dx = \dfrac{du}{-2 x}\right]\quad\halmos$$

15. Compute $\displaystyle \int \dfrac{x^2}{(x^2 - 9)^{3/2}}\,dx$ .

$$\int \dfrac{x^2}{(x^2 - 9)^{3/2}}\,dx = \int \dfrac{9 (\sec \theta)^2}{(9 (\sec \theta)^2 - 9)^{3/2}} \cdot 3 \sec \theta \tan \theta\,d\theta = \int \dfrac{27 (\sec \theta)^3 \tan \theta} {27((\sec \theta)^2 - 1)^{3/2}}\,d\theta = \int \dfrac{(\sec \theta)^3 \tan \theta} {((\tan \theta)^2)^{3/2}}\,d\theta =$$

$$\hfil\raise0.5in\hbox{$\left[x = 3 \sec \theta, \quad dx = 3 \sec \theta \tan \theta\,d\theta\right]$} \hskip0.5in \hbox{\epsfysize=1in \epsffile{rev1-11.eps}}\hfil$$

$$\int \dfrac{(\sec \theta)^3 \tan \theta} {(\tan \theta)^3}\,d\theta = \int \dfrac{(\sec \theta)^3}{(\tan \theta)^2}\,d\theta = \int \dfrac{1}{(\cos \theta)^3} \cdot \dfrac{(\cos \theta)^2}{(\sin \theta)^2}\,d\theta = \int \dfrac{1}{(\cos \theta)(\sin \theta)^2}\,d\theta =$$

$$\int \dfrac{(\sin \theta)^2 + (\cos \theta)^2} {(\cos \theta)(\sin \theta)^2}\,d\theta = \int \left(\dfrac{(\sin \theta)^2}{(\cos \theta)(\sin \theta)^2} + \dfrac{(\cos \theta)^2} {(\cos \theta)(\sin \theta)^2}\right)\,d\theta = \int \left(\dfrac{1}{\cos \theta} + \dfrac{\cos \theta}{(\sin \theta)^2}\right)\,d\theta =$$

$$\int \left(\sec \theta + \csc \theta \cot \theta\right)\,d\theta = \ln |\sec \theta + \tan \theta| - \csc \theta + c = \ln \left|\dfrac{x}{3} + \dfrac{\sqrt{x^2 - 9}}{3}\right| - \dfrac{3}{\sqrt{x^2 - 9}} + c.\quad\halmos$$

16. Compute $\displaystyle \int \dfrac{x^2}{\sqrt{x^2 + 1}}\,dx$ .

$$\int \dfrac{x^2}{\sqrt{x^2 + 1}}\,dx = \int \dfrac{(\tan \theta)^2}{\sqrt{(\tan \theta)^2 + 1}} (\sec \theta)^2\,d\theta = \int \dfrac{(\tan \theta)^2}{\sqrt{(\sec \theta)^2}} (\sec \theta)^2\,d\theta = \int \dfrac{(\tan \theta)^2}{\sec \theta} (\sec \theta)^2\,d\theta =$$

$$\hfil\raise0.5in\hbox{$\left[x = \tan \theta, \quad dx = (\sec \theta)^2\,d\theta\right]$} \hskip0.5in \hbox{\epsfysize=1in \epsffile{rev1-10.eps}}\hfil$$

$$\int \sec \theta(\tan \theta)^2\,d\theta = \int \sec \theta\left((\sec \theta)^2 - 1\right)\,d\theta = \int \left((\sec \theta)^3 - \sec \theta\right)\,d\theta =$$

$$\dfrac{1}{2}\sec \theta \tan \theta - \dfrac{1}{2}\ln |\sec \theta+ \tan \theta| + C = \dfrac{1}{2}x\sqrt{x^2 + 1} - \dfrac{1}{2}\ln |\sqrt{x^2 + 1} + x| + C.\quad\halmos$$

17. Compute $\displaystyle \int \dfrac{-x + 18}{x^2 - 8 x + 12}\,dx$ .

Since $x^2 - 8 x + 12 = (x - 6) (x - 2)$ , I have

$$\eqalign{ \dfrac{-x + 18}{(x - 6) (x - 2)} & = \dfrac{a}{x - 6} + \dfrac{b}{x - 2} \cr \noalign{\vskip2pt} -x + 18 & = a (x - 2) + b (x - 6) \cr}$$

Set $x = 6$ . This gives

$$12 = a \cdot 4, \quad\hbox{so}\quad a = 3.$$

Set $x = 2$ . This gives

$$16 = b \cdot (-4), \quad\hbox{so}\quad b = -4.$$

Therefore,

$$\int \dfrac{-x + 18}{(x - 6) (x - 2)}\,dx = \int \left(\dfrac{3}{x - 6} + \dfrac{-4}{x - 2}\right)\,dx = 3 \ln |x - 6| - 4 \ln |x - 2| + C.\quad\halmos$$

18. Compute $\displaystyle \int \dfrac{-3 x^2 + 47 x - 150}{(x - 6)^2 (x + 2)}\,dx$ .

$$\eqalign{ \dfrac{-3 x^2 + 47 x - 150}{(x - 6)^2 (x + 2)} & = \dfrac{a}{x - 6} + \dfrac{b}{(x - 6)^2} + \dfrac{c}{x + 2} \cr \noalign{\vskip2pt} -3 x^2 + 47 x - 150 & = a (x - 6)(x + 2) + b (x + 2) + c (x - 6)^2 \cr}$$

Set $x = 6$ . This gives

$$24 = b \cdot 8, \quad\hbox{so}\quad b = 3.$$

Set $x = -2$ . This gives

$$-256 = c \cdot 64, \quad\hbox{so}\quad c = -4.$$

Plugging the values for b and c back in yields

$$-3 x^2 + 47 x - 150 = a (x - 6)(x + 2) + 3 (x + 2) - 4 (x - 6)^2.$$

Set $x = 0$ . This gives

$$-150 = a \cdot (-12) + 6 - 144, \quad\hbox{so}\quad a = 1.$$

Thus,

$$\dfrac{-3 x^2 + 47 x - 150}{(x - 6)^2 (x + 2)} = \dfrac{1}{x - 6} + \dfrac{3}{(x - 6)^2} + \dfrac{-4}{x + 2}.$$

Hence,

$$\int \dfrac{-3 x^2 + 47 x - 150}{(x - 6)^2 (x + 2)}\,dx = \int \left(\dfrac{1}{x - 6} + \dfrac{3}{(x - 6)^2} + \dfrac{-4}{x + 2}\right)\,dx =$$

$$\ln |x - 6| - \dfrac{3}{x - 6} - 4 \ln |x + 2| + C.\quad\halmos$$

19. Compute $\displaystyle \int \dfrac{3 + 4 x + 5 x^2 + 3 x^3}{x^2(x + 3)}\,dx$ .

The top and the bottom both have degree 3, so I must divide the top by the bottom:

$$\dfrac{3 + 4 x + 5 x^2 + 3 x^3}{x^2(x + 3)} = 3 + \dfrac{3 + 4 x - 4 x^2}{x^2(x + 3)}.$$

I'll put the 3 aside for now, and work on the fraction:

$$\dfrac{3 + 4 x - 4 x^2}{x^2(x + 3)} = \dfrac{A}{x} + \dfrac{B}{x^2} + \dfrac{C}{x + 3}.$$

Clear denominators:

$$3 + 4 x - 4 x^2 = Ax(x + 3) + B(x + 3) + Cx^2.$$

Set $x = 0$ : I get $3 = 3 B$ , so $B = 1$ .

Set $x = -3$ : I get $-45 = 9C$ , so $C = -5$ .

Plug B and C back in:

$$3 + 4 x - 4 x^2 = Ax(x + 3) + (x + 3) - 5 x^2.$$

Differentiate:

$$4 - 8 x = A(x + 3) + Ax + 1 - 10 x.$$

Set $x = 0$ : I $4 = 3A + 1$ , so $A = 1$ .

Therefore,

$$\dfrac{3 + 4 x - 4 x^2}{x^2(x + 3)} = \dfrac{1}{x} + \dfrac{1}{x^2} - \dfrac{5}{x + 3}.$$

Hence,

$$\dfrac{3 + 4 x + 5 x^2 + 3 x^3}{x^2(x + 3)} = 3 + \dfrac{1}{x} + \dfrac{1}{x^2} - \dfrac{5}{x + 3}.$$

Finally,

$$\int \dfrac{3 + 4 x + 5 x^2 + 3 x^3}{x^2(x + 3)}\,dx = \int \left(3 + \dfrac{1}{x} + \dfrac{1}{x^2} - \dfrac{5}{x + 3}\right)\,dx = 3 x + \ln |x| - \dfrac{1}{x} - 5\ln |x + 3| + C.\quad\halmos$$

20. Compute $\displaystyle \int \dfrac{1}{x^{1/2}(x^{1/3} + x^{1/4})}\,dx$ .

Since the least common multiple of 2, 3, and 4 is 12, I'll let $x = u^{12}$ :

$$\int \dfrac{1}{x^{1/2}(x^{1/3} + x^{1/4})}\,dx = \int \dfrac{12 u^{11}\,du}{u^6(u^4 + u^3)} = 12 \int \dfrac{u^2}{u + 1}\,du = 12 \int \left(u - 1 + \dfrac{1}{u + 1}\right)\,du =$$

$$\left[x = u^{12}, \quad d x= 12 u^{11}\,du\right]$$

$$12 \left(\dfrac{1}{2}u^2 - u + \ln |u + 1|\right) + C = 12 \left(\dfrac{1}{2}x^{1/6} - x^{1/12} + \ln |x^{1/12} + 1|\right) + C.\quad\halmos$$

21. Compute $\displaystyle \int \dfrac{1}{x^{7/8} + x^{5/8}}\,dx$ .

$$\int \dfrac{1}{x^{7/8} + x^{5/8}}\,dx = \int \dfrac{1}{u^7 + u^5} \cdot 8 u^7\,du = 8 \int \dfrac{u^2}{u^2 + 1}\,du = 8 \int \dfrac{(u^2 + 1) - 1}{u^2 + 1}\,du =$$

$$\left[x = u^8, \quad dx = 8 u^7\,du; \quad u = x^{1/8}\right]$$

$$8 \int \left(\dfrac{u^2 + 1}{u^2 + 1} - \dfrac{1}{u^2 + 1}\right)\,du = 8 \int \left(1 - \dfrac{1}{u^2 + 1}\right)\,du = 8 \left(u - \tan^{-1} u\right) + c = 8 \left(x^{1/8} - \tan^{-1} x^{1/8}\right) + c.\quad\halmos$$

22. Compute $\displaystyle \int \dfrac{1}{\sqrt{7 + 6 x - x^2}}\,dx$ .

Complete the square:

$$\eqalign{ 7 + 6 x - x^2 & = -[x^2 - 6 x - 7] \cr & = -[x^2 - 6 x + 9 - 16] \cr & = -[(x - 3)^2 - 16] \cr & = 16 - (x - 3)^2 \cr}$$

So

$$\int \dfrac{1}{\sqrt{7 + 6 x - x^2}}\,dx = \int \dfrac{1}{\sqrt{16 - (x - 3)^2}}\,dx = \int \dfrac{1}{\sqrt{16 - u^2}}\,du = \sin^{-1} \dfrac{u}{4} + c = \sin^{-1} \dfrac{x - 3}{4} + c.$$

$$\left[u = x - 3 , \quad du = dx\right]\quad\halmos$$

23. Compute $\displaystyle \int \dfrac{1}{x^2 + 10 x + 74}\,dx$ .

Complete the square:

$$\eqalign{ x^2 + 10 x + 74 & = x^2 + 10 x + 25 + 49 \cr & = (x + 5)^2 + 49 \cr}$$

So

$$\int \dfrac{1}{x^2 + 10 x + 74}\,dx = \int \dfrac{1}{(x + 5)^2 + 49}\,dx = \int \dfrac{1}{u^2 + 49}\,du = \dfrac{1}{7} \tan^{-1} \dfrac{u}{7} + c = \dfrac{1}{7} \tan^{-1} \dfrac{x + 5}{7} + c.$$

$$\left[u = x + 5, \quad du = dx\right]\quad\halmos$$

24. Compute $\displaystyle \int \dfrac{x - 2}{x^2 - 8 x + 25}\,dx$ .

Since $\dfrac{1}{2}\cdot (-8) = -4$ and $(-4)^2 = 16$ , I have

$$x^2 - 8 x + 25 = x^2 - 8 x + 16 + 9 = (x - 4)^2 + 9.$$

Therefore,

$$\int \dfrac{x - 2}{x^2 - 8 x + 25}\,dx = \int \dfrac{x - 2}{(x - 4)^2 + 9}\,dx = \int \dfrac{(u + 4) - 2}{u^2 + 9}\,du = \int \dfrac{u + 2}{u^2 + 9}\,du =$$

$$\left[u = x - 4, \quad du = dx; \quad x = u + 4\right]$$

$$\int \dfrac{u}{u^2 + 9}\,du + \int \dfrac{2}{u^2 + 9}\,du = \dfrac{1}{2} \ln |u^2 + 9| + \dfrac{2}{3} \tan^{-1} \dfrac{u}{3} + C = \dfrac{1}{2} \ln |(x - 4)^2 + 9| + \dfrac{2}{3} \tan^{-1} \dfrac{x - 4}{3} + C.$$

I did the first part of the u-integral using the substitution $w = u^2 + 9$ .

25. Compute $\displaystyle \int \dfrac{x + 3}{\sqrt{-x^2 - 6 x - 8}}\,dx$ .

First,

$$-x^2 - 6 x - 8 = -(x^2 + 6 x + 8) = -\left[(x^2 + 6 x + 9) - 1\right] = -\left[(x + 3)^2 - 1\right] = 1 - (x + 3)^2.$$

I note that $\dfrac{6}{2} = 3$ and $3^2 = 9$ , so I needed 9 to complete the square.

Thus,

$$\int \dfrac{x + 3}{\sqrt{-x^2 - 6 x - 8}}\,dx = \int \dfrac{x + 3}{\sqrt{1 - (x + 3)^3}}\,dx = \int \dfrac{u}{\sqrt{1 - u^2}}\,du = \int \dfrac{u}{\sqrt{w}} \cdot \dfrac{dw}{-2 u} =$$

$$\left[u = x + 3, \quad du = dx; w = 1 - u^2, \quad dw = -2 u\,du, \quad du = \dfrac{dw}{-2 u}\right]$$

$$-\dfrac{1}{2} \int \dfrac{1}{\sqrt{w}}\,dw = -\dfrac{1}{2} \cdot 2 \sqrt{w} + C = -\sqrt{1 - u^2} + C = -\sqrt{1 - (x + 3)^2} + C.\quad\halmos$$

26. Compute $\displaystyle \int \dfrac{1}{2 x^2 + 8 x + 10}\,dx$ .

$$\int \dfrac{1}{2 x^2 + 8 x + 10}\,dx = \dfrac{1}{2} \int \dfrac{1}{x^2 + 4 x + 5}\,dx = \dfrac{1}{2} \int \dfrac{1}{(x^2 + 4 x + 4) + 1}\,dx = \dfrac{1}{2} \int \dfrac{1}{(x + 2)^2 + 1}\,dx =$$

$$\dfrac{1}{2} \tan^{-1} (x + 2) + C.$$

I completed the square by noting that $\dfrac{4}{2} = 2$ and $2^2 = 4$ . You can do the integral using $u = x + 2$ .

27. Compute $\displaystyle \int \dfrac{6 x^3 - 24 x^2 + 16 x + 4}{x^4 - 4 x^3 + 4 x^2}\,dx$ .

First, $x^4 - 4 x^3 + 4 x^2 = x^2(x - 2)^2$ .

$$\eqalign{ \dfrac{6 x^3 - 24 x^2 + 16 x + 4}{x^2(x - 2)^2} & = \dfrac{a}{x} + \dfrac{b}{x^2} + \dfrac{c}{x - 2} + \dfrac{d}{(x - 2)^2} \cr 6 x^3 - 24 x^2 + 16 x + 4 & = a x(x - 2)^2 + b(x - 2)^2 + c x^2 (x - 2) + d x^2 \cr}$$

Set $x = 0$ . I get $4 = 4 b$ , so $b = 1$ .

Set $x = 2$ . I get $-12 = 4 d$ , so $d = -3$ .

Then

$$6 x^3 - 24 x^2 + 16 x + 4 = a x(x - 2)^2 + (x - 2)^2 + c x^2 (x - 2) - 3 x^2.$$

At this point, you can plug other numbers in for x, or differentiate the equation and then plug numbers in. The idea is to get equations for a and c which you can solve.

For example, set $x = 1$ . I get

$$2 = a + 1 - c - 3, \quad\hbox{or}\quad 4 = a - c.$$

Set $x = -1$ . I get

$$-42 = -9 a + 9 - 3 c - 3, \quad\hbox{or}\quad 16 = 3 a + c.$$

I have to solve $4 = a - c$ and $16 = 3 a + c$ . You can do this in various ways.

For instance, if I add the equations $4 = a - c$ and $16 = 3 a + c$ , I get $20 = 4 a$ , so $a = 5$ . Then plugging $a = 5$ into $4 = a - c$ , I get $4 = 5 - c$ , so $c = 1$ .

Thus,

$$\int \dfrac{6 x^3 - 24 x^2 + 16 x + 4}{x^4 - 4 x^3 + 4 x^2}\,dx = \int \left(\dfrac{5}{x} + \dfrac{1}{x^2} + \dfrac{1}{x - 2} - \dfrac{3}{(x - 2)^2}\right)\,dx = 5 \ln |x| - \dfrac{1}{x} + \ln |x - 2| + \dfrac{3}{x - 2} + C.\quad\halmos$$

28. Compute $\displaystyle \int \dfrac{4 x^3 + 2 x^2 + 16 x +11}{(x^2 + 1)(x^2 + 4)}\,dx$ .

$$\eqalign{ \dfrac{4 x^3 + 2 x^2 + 16 x + 11}{(x^2 + 1)(x^2 + 4)} & = \dfrac{a x + b}{x^2 + 1} + \dfrac{c x + d}{x^2 + 4} \cr 4 x^3 + 2 x^2 + 16 x + 11 & = (a x + b)(x^2 + 4) + (c x + d)(x^2 + 1) \cr}$$

Set $x = 0$ : This gives

$$11 = 4 b + d. \eqno{(1)}$$

Differentiate the last x-equation (using the Product Rule on the two terms on the right):

$$12 x^2 + 4 x + 16 = (a x + b)(2 x) + a(x^2 + 4) + (c x + d)(2 x) + c(x^2 + 1).$$

Set $x = 0$ :

$$16 = 4 a + c. \eqno{(2)}$$

Differentiate the last x-equation:

$$24 x + 4 = (a x + b)(2) + (a)(2 x) + (a)(2 x) + (c x + d)(2) + (c)(2 x) + (c)(2 x).$$

Set $x = 0$ :

$$4 = 2 b + 2 d, \quad\hbox{so}\quad 2 = b + d. \eqno{(3)}$$

Differentiate the last x-equation:

$$24 = 2 a + 2 a + 2 a + 2 c + 2 c + 2 c, \quad\hbox{so}\quad 4 = a + c. \eqno{(4)}$$

Solving (1) ($11 = 4 b + d$ ) together with (3) ($2 = b + d$ ) gives $b = 3$ and $d = -1$ .

Solving (2) ($16 = 4 a + c$ ) together with (4) ($4 = a + c$ ) gives $a = 4$ and $c = 0$ .

Thus, I have

$$\int \dfrac{4 x^3 + 2 x^2 + 16 x + 11}{(x^2 + 1)(x^2 + 4)}\,dx = \int \left(\dfrac{4 x}{x^2 + 1} + \dfrac{3}{x^2 + 1} - \dfrac{1}{x^2 + 4}\right)\,dx = 2 \ln (x^2 + 1) + 3 \tan^{-1} x - \dfrac{1}{2} \tan^{-1} \dfrac{x}{2} + C.$$

The first integral is computed using $u = x^2 + 1$ ; the second and third use the inverse tangent formula:

$$\int \dfrac{1}{x^2 + a^2}\,dx = \dfrac{1}{a} \tan^{-1} \dfrac{x}{a} + C.\quad\halmos$$

29. Compute $\displaystyle \int \dfrac{2 x^2 - 9 x + 11}{(x - 1)^3}\,dx$ .

$$\eqalign{ \dfrac{2 x^2 - 9 x + 11}{(x - 1)^3} & = \dfrac{a}{x - 1} + \dfrac{b}{(x - 1)^2} + \dfrac{c}{(x - 1)^3} \cr \noalign{\vskip2pt} 2 x^2 - 9 x + 11 & = a (x - 1)^2 + b (x - 1) + c \cr}$$

Set $x = 1$ : This gives $4 = c$ . Plug this into the last equation:

$$2 x^2 - 9 x + 11 = a (x - 1)^2 + b (x - 1) + 4.$$

There are a number of ways to proceed. For instance, you can plug in two other values for x (say $x = 0$ and $x = 2$ ) to obtain two equations involving a and b, which you can solve simultaneously.

Alternatively, differentiate the last equation:

$$4 x - 9 = 2 a (x - 1) + b.$$

Set $x = 1$ : This gives $-5 = b$ . Plug this into the last equation:

$$4 x - 9 = 2 a (x - 1) - 5.$$

Set $x = 0$ : This gives

$$\eqalign{ -9 & = -2 a - 5 \cr -4 & = -2 a \cr 2 & = a \cr}$$

Plugging $a = 2$ , $b = -5$ , and $c = 4$ into the original decomposition, I have

$$\int \dfrac{2 x^2 - 9 x + 11}{(x - 1)^3}\,dx = \int \left(\dfrac{2}{x - 1} - \dfrac{5}{(x - 1)^2} + \dfrac{4}{(x - 1)^3}\right)\,dx = 2 \ln |x - 1| + \dfrac{5}{x - 1} - \dfrac{2}{(x - 1)^2} + C.\quad\halmos$$

30. How would you try to decompose $\dfrac{2(x - 2)^2}{x^4(x^2 + 4)^3}$ using partial fractions?

$$\dfrac{2(x - 2)^2}{x^4(x^2 + 4)^3} = \dfrac{A}{x} + \dfrac{B}{x^2} + \dfrac{C}{x^3} + \dfrac{D}{x^4} + \dfrac{E x + F}{x^2 + 4} + \dfrac{G x + H}{(x^2 + 4)^2} + \dfrac{I x + J}{(x^2 + 4)^3}.\quad\halmos$$

31. What is wrong with the following "partial fractions decomposition"?

$$\dfrac{5 x}{(x - 1)^2(x + 1)} = \dfrac{A}{(x - 1)^2} + \dfrac{B}{x + 1}?$$

Partial fractions is the opposite of combining fractions over a common denominator. In this case, the question is: "What fractions would add up to $\dfrac{5 x}{(x - 1)^2(x + 1)}$ ?" The decompositions above could occur, since it has $(x - 1)^2(x + 1)$ as the common denominator.

However, since you don't know beforehand what the fractions are, you must assume the "worst case" --- namely, that there might be an $\dfrac{A}{x - 1}$ term. And in fact, there is --- if you work out the decomposition, it comes out to

$$\dfrac{5 x}{(x - 1)^2(x + 1)} = -\dfrac{5}{4} \dfrac{1}{x + 1} + \dfrac{5}{4} \dfrac{1}{x - 1} + \dfrac{5}{2} \dfrac{1}{(x - 1)^2}.$$

Notice the term $\dfrac{5}{4} \dfrac{1}{x - 1}$ .

32. What is wrong with the following "partial fractions decomposition"?

$$\dfrac{7}{x(x - 1)} = \dfrac{A}{x} + \dfrac{B}{x} + \dfrac{C}{x - 1}.$$

The first two terms could be combined into a single term $\dfrac{D}{x}$ , so they're redundant. There is no reason to list the same denominator twice.

33. Find the partial fractions decomposition of

$$\dfrac{-3 x^4 + x^3 - 6 x^2 - 3}{x(x^2 + 1)^2}.$$

Try the decomposition

$$\dfrac{-3 x^4 + x^3 - 6 x^2 - 3}{x(x^2 + 1)^2} = \dfrac{A}{x} + \dfrac{Bx + C}{x^2 + 1} + \dfrac{Dx + E}{(x^2 + 1)^2}.$$

Clear denominators:

$$-3 x^4 + x^3 - 6 x^2 - 3 = A(x^2 + 1)^2 + (Bx + C)(x)(x^2 + 1) + (Dx + E)(x).$$

Set $x = 0$ : I get $A = -3$ . Plug it back in:

$$-3 x^4 + x^3 - 6 x^2 - 3 = -3(x^2 + 1)^2 + (Bx + C)(x)(x^2 + 1) + (Dx + E)(x).$$

Differentiate:

$$12 x^3 + 3 x^2 - 12 x = -12 x(x^2 + 1) + B(x^3 + x) + (Bx + C)(3 x^2 + 1) + 2Dx + E.$$

Set $x = 0$ : I get $C + E = 0$ .

Differentiate again:

$$-36 x^2 + 6 x - 12 = -36 x^2 - 12 + B(3 x^2 + 1) + B(3 x^2 + 1) + (Bx + C)(6 x) + 2D.$$

Set $x = 0$ : I get $B + D = 0$ .

Cancel the $-36 x^2$ and -12 terms in the previous equation, then differentiate:

$$6 x = B(3 x^2 + 1) + B(3 x^2 + 1) + (Bx + C)(6 x) + 2D,$$

$$6 = 6 B x + 6 B x + 6 B x + (Bx + C)(6).$$

Set $x = 0$ : I get $C = 1$ . Since $C + E = 0$ , it follows that $E = -1$ .

Plug $C = 1$ back in, then simplify the equation:

$$6 = 24 B x + 6, \quad\quad\hbox{or}\quad\quad 0 = 24 Bx.$$

Set $x = 1$ : I get $B = 0$ . But $B + D = 0$ , so $D = 0$ .

Hence,

$$\dfrac{-3 x^4 + x^3 - 6 x^2 - 3}{x(x^2 + 1)^2} = -\dfrac{3}{x} + \dfrac{1}{x^2 + 1} - \dfrac{1}{(x^2 + 1)^2}.\quad\halmos$$

34. (a) Compute $\displaystyle \int \dfrac{-x^2 + 8 x - 4}{x(x^2 + x - 2)}\,dx$ .

(b) Calvin Butterball tries to use the antiderivative from (a) to compute

$$\int_{-1}^{1/2} \dfrac{-x^2 + 8 x - 4}{x(x^2 + x - 2)}\,dx.$$

He gets

$$\left[2 \ln |x| + \ln |x - 1| - 4\ln |x + 2|\right]_{-1}^{1/2} = \left(2\ln \dfrac{1}{2} + \ln \dfrac{1}{2} - 4\ln {3}{2}\right) - (2\ln 1 + \ln 2 - 4\ln 1) \approx -4.39445.$$

Does this computation make sense? Why or why not?

(a) $x(x^2 + x - 2) = x(x - 1)(x + 2)$ , so I try

$$\dfrac{-x^2 + 8 x - 4}{x(x^2 + x - 2)} = \dfrac{A}{x} + \dfrac{B}{x - 1} + \dfrac{C}{x + 2}.$$

Clear denominators:

$$-x^2 + 8 x - 4 = A(x - 1)(x + 2) + Bx(x + 2) + Cx(x - 1).$$

Set $x = 0$ : I get $-4 = -2A$ , or $A = 2$ .

Set $x = 1$ : I get $3 = 3 B$ , or $B = 1$ .

Set $x = -2$ : I get $-24 = 6C$ , or $C = -4$ .

Therefore,

$$\int \dfrac{-x^2 + 8 x - 4}{x(x^2 + x - 2)}\,dx = \int \left(\dfrac{2}{x} + \dfrac{1}{x - 1} - \dfrac{4}{x + 2}\right)\,dx = 2\ln |x| + \ln |x - 1| - 4\ln |x + 2| + C.\quad\halmos$$

(b) The computation is incorrect, because the antiderivative is valid only within intervals which don't contain the singularities at $x = -2$ , $x = 0$ , and $x = 1$ . The interval $-1 \le x \le \dfrac{1}{2}$ includes the singularity at $x = 0$ . It is not legal to simply "plug in the endpoints" --- to do this definite integral correctly, you should set it up as two improper integrals.

35. Find the area of the region under $y = \dfrac{x}{(x^2 + 1)^2}$ from $x = 0$ to $\infty$ .

$$\hbox{\epsfysize=1.5in \epsffile{rev1-19.eps}}$$

The area is

$$A = \int_0^\infty \dfrac{x}{(x^2 + 1)^2}\,dx = \lim_{c\to \infty} \int_0^c \dfrac{x}{(x^2 + 1)^2}\,dx = \lim_{c\to \infty} \left[-\dfrac{1}{2(x^2 + 1)}\right]_0^c = -\dfrac{1}{2} \lim_{c\to \infty} \left(\dfrac{1}{c^2 + 1} - 1\right) = \dfrac{1}{2}.$$

Here's the work for the antiderivative:

$$\int \dfrac{x}{(x^2 + 1)^2}\,dx = \int \dfrac{x}{u^2}\cdot \dfrac{du}{2 x} = \dfrac{1}{2} \int \dfrac{du}{u^2} = -\dfrac{1}{2 u} + C = -\dfrac{1}{2(x^2 + 1)} + C.$$

$$\left[u = x^2 + 1, \quad du = 2 x\,dx, \quad dx = \dfrac{du}{2 x}\right]\quad\halmos$$

36. Compute $\displaystyle \int_4^6 \dfrac{1}{\sqrt{x - 4}}\,dx$ .

Since $\dfrac{1}{\sqrt{x - 4}}$ is undefined at $x = 4$ and $x = 4$ is in the interval of integration (it's one of the endpoints), the integral is improper. I replace the "4" with a parameter a, then take the limit as a approaches 4 from the right.

$$\int_4^6 \dfrac{1}{\sqrt{x - 4}}\,dx = \lim_{a \to 4^+} \int_a^6 \dfrac{1}{\sqrt{x - 4}}\,dx = \lim_{a \to 4^+} \left[2 \sqrt{x - 4}\right]_a^6 = 2 \lim_{a \to 4^+} \left(\sqrt{2} - \sqrt{a - 4}\right) = 2 \sqrt{2}.\quad\halmos$$

37. Compute $\displaystyle \int_{-\infty}^0 x e^{x^2}\,dx$ .

$$\int_{-\infty}^0 x e^{x^2}\,dx = \lim_{b \to -\infty} \int_b^0 x e^{x^2}\,dx = \lim_{b \to -\infty} \int_{b^2}^0 x e^u \cdot \dfrac{du}{2 x} = \dfrac{1}{2} \lim_{b \to -\infty} \int_{b^2}^0 e^u\,du =$$

$$\left[u = x^2, \quad du = 2 x\,dx, \quad dx = \dfrac{du}{2 x}; \quad x = b, \quad u = b^2; \quad x = 0, \quad u = 0\right]$$

$$\dfrac{1}{2} \lim_{b \to -\infty} \left[e^u\right]_{b^2}^0 = \dfrac{1}{2} \lim_{b \to -\infty} \left(1 - e^{b^2}\right).$$

As $b \to -\infty$ , I have $b^2 \to \infty$ , and $e^{b^2} \to \infty$ . Therefore, the integral diverges (to $-\infty$ , since the $e^{b^2}$ term was negated).

38. Compute $\displaystyle \int_0^\infty x e^{-3 x}\,dx$ .

$$\int_0^\infty x e^{-3 x}\,dx = \lim_{b \to +\infty} \int_0^b x e^{-3 x}\,dx = \lim_{b \to +\infty} \left[-\dfrac{1}{3} x e^{-3 x} - \dfrac{1}{9} e^{-3 x}\right]_0^b =$$

$$\lim_{b \to +\infty} \left(-\dfrac{1}{3} b e^{-3 b} - \dfrac{1}{9} e^{-3 b} + \dfrac{1}{9}\right) = -0 - 0 + \dfrac{1}{9} = \dfrac{1}{9}.$$

Here's the work for the two limits:

$$\lim_{b \to +\infty} e^{-3 b} = \lim_{b \to +\infty} \dfrac{1}{e^{3 b}} = 0,$$

$$\lim_{b \to +\infty} b e^{-3 b} = \lim_{b \to +\infty} \dfrac{b}{e^{3 b}} = \lim_{b \to +\infty} \dfrac{1}{3 e^{3 b}} = 0.$$

I used L'Hôpital's Rule to compute the second limit.

Here's the work for the antiderivative:

$$\matrix{& \der {} x & & \displaystyle \int\,dx \cr & & & \cr + & x & & e^{-3 x} \cr & & \searrow & \cr - & 1 & & -\dfrac{1}{3} e^{-3 x} \cr & & \searrow & \cr + & 0 & & \dfrac{1}{9} e^{-3 x} \cr}$$

$$\int xe^{-3 x}\,dx = -\dfrac{1}{3} x e^{-3 x} - \dfrac{1}{9} e^{-3 x} + C.\quad\halmos$$

39. Compute $\displaystyle \int_0^\infty \cos 3 x\,dx$ .

$$\int_0^\infty \cos 3 x\,dx = \lim_{k \to \infty} \int_0^k \cos 3 x\,dx = \lim_{k \to \infty} \left[\dfrac{1}{3} \sin 3 x\right]_0^k = \lim_{k \to \infty} \dfrac{1}{3} \sin 3 k.$$

$\displaystyle \lim_{k \to \infty} \sin 3 k$ is undefined. Hence, the integral diverges. (It doesn't diverge to $\infty$ or $-\infty$ ; the limit is simply undefined.)

40. Compute $\displaystyle \int_1^\infty \dfrac{x^2 + 4}{x^3 + 12 x + 1}\,dx$ .

Do the antiderivative:

$$\int \dfrac{x^2 + 4}{x^3 + 12 x + 1}\,dx = \int \dfrac{x^2 + 4}{u} \cdot \dfrac{du}{3 (x^2 + 4)} = \dfrac{1}{3} \int \dfrac{1}{u}\,du = \dfrac{1}{3} \ln |u| + c = \dfrac{1}{3} \ln |x^3 + 12 x + 1| + c.$$

$$\left[u = x^3 + 12 x + 1, \quad du = (3 x^2 + 12)\,dx = 3(x^2 + 4), \quad dx = \dfrac{du}{3 (x^2 + 4)}\right]$$

Do the integral:

$$\int_1^\infty \dfrac{x^2 + 4}{x^3 + 12 x + 1}\,dx = \lim_{b \to \infty} \int_1^b \dfrac{x^2 + 4}{x^3 + 12 x + 1}\,dx = \lim_{b \to \infty} \left[\dfrac{1}{3} \ln |x^3 + 12 x + 1|\right]_1^b =$$

$$\dfrac{1}{3} \lim_{b \to \infty} \left(\ln |b^3 + 12 b + 1| - \ln 14\right) = +\infty.$$

(Note that $\displaystyle \lim_{b \to \infty} \ln |b^3 + 12 b + 1| = +\infty$ .)

The integral diverges to $+\infty$ .

41. Compute $\displaystyle \int_1^\infty \dfrac{x^2 + 4}{(x^3 + 12 x + 1)^2}\,dx$ .

Do the antiderivative:

$$\int \dfrac{x^2 + 4}{(x^3 + 12 x + 1)^2}\,dx = \int \dfrac{x^2 + 4}{u^2} \cdot \dfrac{du}{3 (x^2 + 4)} = \dfrac{1}{3} \int \dfrac{1}{u^2}\,du = \dfrac{1}{3} \cdot \dfrac{-1}{u} + c = -\dfrac{1}{3} \dfrac{1}{x^3 + 12 x + 1} + c.$$

$$\left[u = x^3 + 12 x + 1, \quad du = (3 x^2 + 12)\,dx = 3(x^2 + 4), \quad dx = \dfrac{du}{3 (x^2 + 4)}\right]$$

Do the integral:

$$\int_1^\infty \dfrac{x^2 + 4}{(x^3 + 12 x + 1)^2}\,dx = \lim_{b \to \infty} \int_1^b \dfrac{x^2 + 4}{(x^3 + 12 x + 1)^2}\,dx = \lim_{b \to \infty} \left[-\dfrac{1}{3} \dfrac{1}{x^3 + 12 x + 1}\right]_1^b =$$

$$-\dfrac{1}{3} \lim_{b \to \infty} \left(\dfrac{1}{b^3 + 12 b + 1} - \dfrac{1}{14}\right) = \dfrac{1}{42}.$$

(Note that $\displaystyle \lim_{b \to \infty} \dfrac{1}{b^3 + 12 b + 1} = 0$ .)

The integral converges to $\dfrac{1}{42}$ .

42. Compute $\displaystyle \int_2^{11} \dfrac{1}{{\root 3 \of {x - 3}}}\,dx$ .

$$\int_2^{11} \dfrac{1}{{\root 3 \of {x - 3}}}\,dx = \int_2^3 \dfrac{1}{{\root 3 \of {x - 3}}}\,dx + \int_3^{11} \dfrac{1}{{\root 3 \of {x - 3}}}\,dx.$$

The first integral is

$$\int_2^3 \dfrac{1}{{\root 3 \of {x - 3}}}\,dx = \lim_{a\to 3-} \int_2^a \dfrac{1}{{\root 3 \of {x - 3}}}\,dx = \lim_{a\to 3-} \left[\dfrac{3}{2} (x - 3)^{2/3}\right]_2^a = \dfrac{3}{2} \lim_{a\to 3-} \left((a - 3)^{2/3} - 1\right) = -\dfrac{3}{2}.$$

The second integral is

$$\int_3^{11} \dfrac{1}{{\root 3 \of {x - 3}}}\,dx = \lim_{b \to 3+} \int_b^{11} \dfrac{1}{{\root 3 \of {x - 3}}}\,dx = \lim_{b \to 3+} \left[\dfrac{3}{2} (x - 3)^{2/3}\right]_b^{11} = \dfrac{3}{2} \lim_{b \to 3+} \left(4 - (b - 3)^{2/3}\right) = 6.$$

Therefore,

$$\int_2^{11} \dfrac{1}{{\root 3 \of {x - 3}}}\,dx = -\dfrac{3}{2} + 6 = \dfrac{9}{2}.$$

$$\hbox{\epsfysize=1.5in \epsffile{rev1-21.eps}}$$

The graph of $\dfrac{1}{{\root 3 \of {x - 3}}}$ has a vertical asymptote at $x = 3$ , but the (signed) area on each side is finite. The negative area to the left of $x = 3$ partially cancels the positive area to the right of $x = 3$ . Thus, the integral in this problem does not represent the actual area bounded by the graph, the x-axis, and the lines $x = 2$ , $x = 3$ , and $x = 11$ .

In the next few problems, I'll use the following fact. If f and g are integrable functions on every finite interval $[a, b]$ and $f(x) \ge g(x) \ge 0$ , then if $\displaystyle \int_a^\infty f(x)\,dx$ converges, then $\displaystyle \int_a^\infty g(x)\,dx$ converges.

Intuitively, if the bigger function's integral converges to a number, then the smaller function's integral must converge, because it's caught between that number and 0.

43. Prove that $\displaystyle \int_0^\infty e^{-x^4}\,dx$ converges.

The interval of integration is $x \ge 0$ . On this interval, $x \le x^4$ , so $-x \ge -x^4$ , and $e^{-x} \ge e^{-x^4}$ . Therefore, if $\displaystyle \int_0^\infty e^{-x}\,dx$ converges, then $\displaystyle \int_0^\infty e^{-x^4}\,dx$ cconverges.

Now

$$\int_0^\infty e^{-x}\,dx = \lim_{b \to \infty} \int_0^b e^{-x}\,dx = \lim_{b \to \infty} \left[-e^{-x}\right]_0^b = \lim_{b \to \infty} \left(-e^{-b} + 1\right) = -0 + 1 = 1.$$

Since $\displaystyle \int_0^\infty e^{-x}\,dx$ converges, it follows that $\displaystyle \int_0^\infty e^{-x^4}\,dx$ converges as well.

44. Prove that $\displaystyle \int_0^\infty \dfrac{(\sin x)^2}{x^2 + 1}\,dx$ converges.

I have

$$\eqalign{ (\sin x)^2 & \le 1 \cr \noalign{\vskip2pt} \dfrac{(\sin x)^2}{x^2 + 1} & \le \dfrac{1}{x^2 + 1} \cr}$$

(I built up from a known fact about trig functions to get an inequality with the function I'm trying to integrate on the "small" side.)

Now

$$\int_0^\infty \dfrac{1}{x^2 + 1}\,dx = \lim_{b \to \infty} \int_0^b \dfrac{1}{x^2 + 1}\,dx = \lim_{b \to \infty} \left[\tan^{-1} x\right]_0^b = \dfrac{\pi}{2}.$$

Since $\displaystyle \int_0^\infty \dfrac{1}{x^2 + 1}\,dx$ converges and $\dfrac{1}{x^2 + 1} \ge \dfrac{(\sin x)^2}{x^2 + 1} \ge 0$ , it follows that $\displaystyle \int_0^\infty \dfrac{(\sin x)^2}{x^2 + 1}\,dx$ converges as well.

45. (a) Show that the following integrals both diverge:

$$\int_0^\infty x\,dx \quad\hbox{and}\quad \int_{-\infty}^0 x\,dx.$$

(It follows that $\displaystyle \int_{-\infty}^\infty x\,dx$ diverges as well.)

(b) Show that $\displaystyle \lim_{b \to \infty} \int_{-b}^b x\,dx$ converges. (This is called the Cauchy principal value of the integral; this problem shows that $\displaystyle \lim_{b \to \infty} \int_{-b}^b x\,dx$ is not the same as $\displaystyle \int_{-\infty}^\infty x\,dx$ .)

(a)

$$\int_0^\infty x\,dx = \lim_{b \to \infty} \int_0^b x\,dx = \lim_{b \to \infty} \left[\dfrac{1}{2} x^2\right]_0^b = \lim_{b \to \infty} \dfrac{1}{2} b^2 = \infty.$$

$$\int_{-\infty}^0 x\,dx = \lim_{b \to -\infty} \int_b^0 x\,dx = \lim_{b \to -\infty} \left[\dfrac{1}{2} x^2\right]_b^0 = \lim_{b \to -\infty} \left(-\dfrac{1}{2} b^2\right) = -\infty.\quad\halmos$$

(b)

$$\lim_{b \to \infty} \int_{-b}^b x\,dx = \lim_{b \to \infty} \left[\dfrac{1}{2} x^2\right]_{-b}^b = \lim_{b \to \infty} \left(\dfrac{1}{2} b^2 - \dfrac{1}{2} b^2\right) = \lim_{b \to \infty} 0 = 0.\quad\halmos$$

To think is not enough; you must think of something. - Jules Renard

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga