Review Problems for Test 2

Math 211

These problems are provided to help you study. The presence of a problem on this sheet does not imply that a similar problem will appear on the test. And the absence of a problem from this sheet does not imply that the test will not have a similar problem.

1. Find the area of the region bounded by the graphs of $y = x^2 - 3 x$ and $y = 15 - x$ .

2. Find the area of the region between $y = x^2 - x$ and $y = x + 8$ from $x = 0$ to $x = 5$ .

3. Find the area of the region bounded by $y = x^2 - 2 x - 8$ and $y = -x^2 + 4 x + 12$ .

4. Find the area of the region bounded by $x = \cos y$ and $x = \sin y$ , between the first two intersections of the curves for which $y > 0$ .

5. The region bounded by $y = 4 x - x^2$ and the x-axis is revolved about the x-axis. Find the volume of the solid that is generated.

6. Consider the region in the x-y plane bounded by $y = e^x$ , the line $y = 1$ , and the line $x = 1$ . Find the volume generated by revolving the region:

(a) About the line $y = 1$ .

(b) About the line $x = 2$ .

(c) About the line $y = e$ .

7. The base of a solid is the region in the x-y plane bounded by the curves $y = x^2$ and $y = x + 2$ . The cross-sections of the solid perpendicular to the x-y plane and the x-axis are isosceles right triangles with one leg in the x-y plane. Find the volume of the solid.

8. The base of a solid is the region in the x-y-plane bounded above by the line $y = 1$ and below by the parabola $y = x^2$ . The cross-sections in planes perpendicular to the y-axis are squares having one edge in the x-y-plane. Find the volume of the solid.

9. The region which lies above the x-axis and below the graph of $y = \dfrac{1}{x^2 + 1}$ , $-\infty < x < \infty$ , is revolved about the x-axis. Find the volume of the solid which is generated.

Hint:

$$\int \dfrac{1}{(x^2 + 1)^2}\,dx = \dfrac{1}{2} \dfrac{x}{x^2 + 1} + \dfrac{1}{2}\tan^{-1} x + C.$$

10. A force of 8 pounds is required to extend a spring 2 feet beyond its unstretched length.

(a) Find the spring constant k.

(b) Find the work done in stretching the spring from 2 feet beyond its unstretched length to 3 feet beyond its unstretched length.

11. The base of a rectangular tank is 2 feet long and 3 feet wide; the tank is 6 feet high. Find the work done in pumping all the water out of the top of the tank.

12. Write a formula for the n-th term of the sequence, assuming that the terms continue in the "obvious" way.

(a) $7, 11, 15, 19, 23, 27, \ldots$ .

(b) $\dfrac{2}{8}, \dfrac{4}{13}, \dfrac{6}{18}, \dfrac{8}{23}, \ldots$ .

13. A sequence is defined recursively by

$$a_{n + 1} = 3 a_n + 5 \quad\hbox{for}\quad n \ge 0 \quad\hbox{and}\quad a_0 = 1.$$

Write down the first 5 terms of the sequence.

14. Determine whether the sequence $a_n = \dfrac{e^n}{n + 1}$ for $n \ge 1$ eventually increases, decreases, or neither increases nor decreases.

15. Determine whether the sequence $a_n = \cos (\pi n)$ for $n \ge 0$ eventually increases, decreases, or neither increases nor decreases.

16. Is the following sequence bounded? Why or why not?

$$1,\ 1,\ 1,\ 2,\ 1,\ 3\, \ldots 1,\ n,\ \ldots .$$

17. Determine whether the sequence converges or diverges; if it converges, find the limit.

(a) $\displaystyle \left\{1.0001^n\right\}$ .

(b) $\displaystyle \left\{\dfrac{e^n + 3^n}{2^n + \pi^n}\right\}$ .

(c) $\displaystyle \left\{\dfrac{2 n^3 - 5 n + 7}{7 n^2 - 13 n^3}\right\}$ .

(d) $\displaystyle \left\{\left(\tan^{-1} n\right)^2\right\}$ .

(e) $\displaystyle \left\{\dfrac{\sin n}{n^2}\right\}$ .

(f) $\displaystyle \left\{\left(\dfrac{4 n + 1}{9 n + 17} + e^{-n^2}\right)^n\right\}$ .

18. A sequence is defined recursively by

$$a_1 = 5, \quad a_{n+1} = \sqrt{6 a_n + 27} \quad\hbox{for}\quad n \ge 1.$$

Find $\displaystyle \lim_{n \to \infty} a_n$ .

19. If the series converges, find the exact value of its sum; if it diverges, explain why.

(a) $\displaystyle \sum_{n = 1}^\infty \left(-\dfrac{1}{5}\right)^n$ .

(b) $\displaystyle \sum_{n = 1}^\infty (-1.021)^n$ .

(c)

$$\dfrac{3}{5^3} + \dfrac{3}{5^4} + \dfrac{3}{5^5} + \cdots + \dfrac{3}{5^n} + \cdots.$$

(d) $\displaystyle \sum_{n = 2}^\infty \left(\dfrac{6^n}{7^n} + 2 \cdot \dfrac{(-1)^n}{4^n}\right)$ .

(e) $\displaystyle \sum_{n = 3}^\infty \left(\dfrac{5^n}{4^n} + \dfrac{4^n}{5^n}\right)$ .

(f) $\displaystyle \sum_{n = 3}^\infty \ln \dfrac{n}{n +1}$ .

20. (a) Find the partial fractions decomposition of $\dfrac{2}{(2 k + 1)(2 k + 3)}$ .

(b) Use (a) to find the sum of the series

$$\sum_{k = 1}^{\infty} \dfrac{2}{(2 k + 1)(2 k + 3)}.$$

21. Find series $\displaystyle \sum_{n = 1}^\infty a_n$ and $\displaystyle \sum_{n = 1}^\infty b_n$ such that both series diverge, and:

(a) $\displaystyle \sum_{n = 1}^\infty (a_n + b_n)$ diverges.

(b) $\displaystyle \sum_{n = 1}^\infty (a_n + b_n)$ converges.

22. Calvin Butterball notes that $\displaystyle \lim_{n \to \infty} \dfrac{1}{\sqrt{n}} = 0$ , and concludes that the series $\displaystyle \sum_{n = 1}^\infty \dfrac{1}{\sqrt{n}}$ converges by the Zero Limit Test. What's wrong with his reasoning?

23. If the series $\displaystyle \sum_{k = 17}^{\infty} a_k$ , converges, does the series $\displaystyle \sum_{k = 1}^{\infty} a_k$ converge?

24. Does the series $\displaystyle \sum_{k = 1}^\infty (-1)^{k+1} \dfrac{2 k + 1}{4 k + 3}$ converge?

25. Determine whether the series converges or diverges: $\displaystyle \sum_{k = 1}^{\infty} \dfrac{3^k + 2^k}{6^k}$ .

26. Determine whether the series converges or diverges:$\displaystyle \sum_{k = 3}^{\infty} \dfrac{k^2 - 3 k + 2}{k^4}$ .

27. Determine whether the series converges or diverges: $\displaystyle \sum_{k = 1}^{\infty} \sqrt{\tan^{-1} k}$ .

28. Determine whether the series converges or diverges: $\displaystyle \sum_{k = 1}^{\infty} \dfrac{1}{k^{1.05}}$ .

29. Determine whether the series converges or diverges: $\displaystyle \sum_{k=2}^{\infty} \dfrac{1}{k (\ln k)^2}$ .

30. Determine whether the series converges or diverges: $\displaystyle \sum_{k = 1}^{\infty} \dfrac{2}{3 k + 5}$ .

31. Determine whether the series converges or diverges: $\displaystyle \sum_{k = 1}^{\infty} \dfrac{e^x}{e^{2 x} + 1}$ .

Solutions to the Review Problems for Test 2

1. Find the area of the region bounded by the graphs of $y = x^2 - 3 x$ and $y = 15 - x$ .

$$\hbox{\epsfysize=1.5in \epsffile{rev2-22.eps}}$$

The curves intersect at $x = -3$ and at $x = 5$ :

$$\eqalign{ x^2 - 3 x & = 15 - x \cr x^2 - 2 x - 15 & = 0 \cr (x - 5)(x + 3) & = 0 \cr x = 5 & \quad\hbox{or}\quad x = -3 \cr}$$

$y = 15 - x$ is the top curve and $y = x^2 - 3 x$ is the bottom curve. Hence, the area is

$$\int_{-3}^5 \left((15 - x) - (x^2 - 3 x)\right)\,dx = \int_{-3}^5 \left(15 + 2 x - x^2\right)\,dx = \left[15 x + x^2 - \dfrac{1}{3}x^3\right]_{-3}^5 = \dfrac{256}{3}.\quad\halmos$$

2. Find the area of the region between $y = x^2 - x$ and $y = x + 8$ from $x = 0$ to $x = 5$ .

$$\hbox{\epsfysize=1.5in \epsffile{rev2-25.eps}}$$

The curves intersect at $x = 4$ and $x = -2$ :

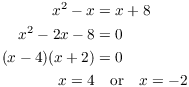
$$\eqalign{ x^2 - x & = x + 8 \cr x^2 - 2 x - 8 & = 0 \cr (x - 4)(x + 2) & = 0 \cr x = 4 & \quad\hbox{or}\quad x = -2 \cr}$$

Since the curves cross between 0 and 5, I will need two integrals. On the left-hand piece, the top curve is $y = x + 8$ and the bottom curve is $y = x^2 - x$ . On the right-hand piece, the top curve is $y = x^2 - x$ and the bottom curve is $y = x + 8$ . The area is

$$\int_0^4 \left((x + 8) - (x^2 - x)\right)\,dx + \int_4^5 \left((x^2 - x) - (x + 8)\right)\,dx = \int_0^4 (-x^2 + 2 x + 8)\,dx + \int_4^5 (x^2 - 2 x - 8)\,dx =$$

$$\left[-\dfrac{1}{3}x^3 + x^2 + 8 x\right]_0^4 + \left[\dfrac{1}{3}x^3 - x^2 - 8 x\right]_4^5 = 30.\quad\halmos$$

3. Find the area of the region bounded by $y = x^2 - 2 x - 8$ and $y = -x^2 + 4 x + 12$ .

$$\hbox{\epsfysize=1.5in \epsffile{rev2-3.eps}}$$

$$\eqalign{ x^2 - 2 x - 8 & = -x^2 + 4 x + 12 \cr 2 x^2 - 6 x - 20 & = 0 \cr x^2 - 3 x - 10 & = 0 \cr (x - 5)(x + 2) & = 0 \cr}$$

The curves intersect at $x = 5$ and $x = -2$ . The top curve is $y = -x^2 + 4 x + 12$ and the bottom curve is $y = x^2 - 2 x - 8$ . The area is

$$\int_{-2}^5 \left((-x^2 + 4 x + 12) - (x^2 - 2 x - 8)\right)\,dx = \int_{-2}^5 (-2 x^2 + 6 x + 20)\,dx = \left[-\dfrac{2}{3} x^3 + 3 x^2 + 20 x\right]_{-2}^5 =$$

$$\dfrac{343}{3} = 114.33333 \ldots.\quad\halmos$$

4. Find the area of the region bounded by $x = \cos y$ and $x = \sin y$ , between the first two intersections of the curves for which $y > 0$ .

$$\hbox{\epsfysize=1.75in \epsffile{rev2-13.eps}}$$

Solve the curve equations simultaneously:

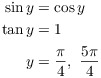
$$\eqalign{ \sin y & = \cos y \cr \tan y & = 1 \cr y & = \dfrac{\pi}{4},\ \dfrac{5\pi}{4} \cr}$$

Break the region up into horizontal rectangles. The length of a typical rectangle is $\sin y - \cos y$ . The area is

$$\int_{\pi/4}^{5\pi/4} (\sin y - \cos y)\,dy = \left[-\cos y - \sin y\right]_{\pi/4}^{5\pi/4} = 2 \sqrt{2} = 2.82842 \ldots.\quad\halmos$$

5. The region bounded by $y = 4 x - x^2$ and the x-axis is revolved about the x-axis. Find the volume of the solid that is generated.

$$\hbox{\epsfysize=1.5in \epsffile{rev2-24.eps}}$$

The region extends from $x = 0$ to $x = 4$ . I'll use circular slices. The radius of a typical slice is $r = y = 4 x - x^2$ . The area of a typical slice is

$$\pi r^2 = \pi(4 x - x^2)^2 = \pi(16 x^2 - 8 x^3 + x^4).$$

The volume generated is

$$V = \int_0^4 \pi(16 x^2 - 8 x^3 + x^4)\,dx = \pi\left[\dfrac{16}{3}x^3 - 2 x^4 + \dfrac{1}{5}x^5\right]_0^4 = \dfrac{512 \pi}{15} = 107.23302 \ldots.\quad\halmos$$

6. Consider the region in the x-y plane bounded by $y = e^x$ , the line $y = 1$ , and the line $x = 1$ . Find the volume generated by revolving the region:

(a) About the line $y = 1$ .

(b) About the line $x = 2$ .

(c) About the line $y = e$ .

(a)

$$\hbox{\epsfysize=2in \epsffile{rev2-8a.eps}}$$

Since the solid has no "holes" or "gaps" in its interior, I can use circular slices. The radius of a slice is $r = e^x - 1$ , so the volume is

$$V = \int_0^1 \pi(e^x - 1)^2\,dx = \pi \int_0^1 (e^{2 x} - 2 e^x + 1)\,dx = \pi \left[\dfrac{1}{2}e^{2 x} - 2 e^x + x\right]_0^1 = \dfrac{\pi e^2}{2} - 2 \pi e + \dfrac{5 \pi}{2} = 2.38121 \ldots.\quad\halmos$$

(b)

$$\hbox{\epsfysize=2in \epsffile{rev2-8b.eps}}$$

I'll use cylindrical shells. The height is $h = e^x - 1$ , and the radius is $r = 2 - x$ . The volume is

$$V = \int_0^1 2\pi(e^x - 1)(2 - x)\,dx = 2\pi \int_0^1 \left(2 e^x - 2 - xe^x + x\right)\,dx = 2\pi \left[2 e^x - 2 x - xe^x + e^x + \dfrac{1}{2}x^2\right]_0^1 =$$

$$4 \pi e - 9 \pi = 5.88460 \ldots.$$

Here's the work for part of the integral:

$$\matrix{& \der {} x & & \displaystyle \int\,dx \cr & & & \cr + & x & & e^x \cr & & \searrow & \cr - & 1 & & e^x \cr & & \searrow & \cr + & 0 & \to & e^x \cr}$$

$$\int xe^x\,dx = xe^x - e^x + C.\quad\halmos$$

(c)

$$\hbox{\epsfysize=2in \epsffile{rev2-8c.eps}}$$

I'll use cylindrical shells. Since $y = e^x$ gives $x = \ln y$ , the height is $h = 1 - x = 1 - \ln y$ , and the radius is $r = e - y$ . The vertical limits on the region are $y = 1$ and $y = e$ . The volume is

$$V = \int_1^e 2\pi(1 - \ln y)(e - y)\,dy = 2\pi \int_1^e \left(e - e\ln y - y + y\ln y\right)\,dy =$$

$$2\pi \left[ey - ey\ln y+ ey - \dfrac{1}{2}y^2 + \dfrac{1}{2}y^2\ln y - \dfrac{1}{4}y^2\right]_1^e = \dfrac{3 \pi e^2}{2} - 4 \pi e + \dfrac{3 \pi}{2} = 5.37355 \ldots.$$

Here is how I did two of the pieces of the integral:

$$\matrix{& \der {} y & & \displaystyle \int\,dy \cr & & & \cr + & \ln y & & 1 \cr & & \searrow & \cr - & \dfrac{1}{y} & \to & y \cr}$$

$$\int \ln y\,dy = y\ln y - \int\,dy = y\ln y - y + C.$$

$$\matrix{& \der {} y & & \displaystyle \int\,dy \cr & & & \cr + & \ln y & & y \cr & & \searrow & \cr - & \dfrac{1}{y} & \to & \dfrac{1}{2}y^2 \cr}$$

$$\int y\ln y\,dy = \dfrac{1}{2}y^2\ln y - \dfrac{1}{2}\int y\,dy = \dfrac{1}{2}y^2\ln y - \dfrac{1}{4}y^2 + C.\quad\halmos$$

7. The base of a solid is the region in the x-y plane bounded by the curves $y = x^2$ and $y = x + 2$ . The cross-sections of the solid perpendicular to the x-y plane and the x-axis are isosceles right triangles with one leg in the x-y plane. Find the volume of the solid.

$$\hbox{\epsfysize=2in \epsffile{rev2-9a.eps}} \hskip0.5in \hbox{\epsfysize=2in \epsffile{rev2-9b.eps}}$$

The first picture shows the base of the solid. The second picture shows three typical triangular slices standing on the base.

$$\eqalign{ x^2 & = x + 2 \cr x^2 - x - 2 & = 0 \cr (x - 2)(x + 1) & = 0 \cr x = 2 & \quad\hbox{or}\quad x = -1 \cr}$$

Therefore, the base of the solid extends from $x = -1$ to $x = 2$ .

The leg of a triangular slice has length $x + 2 - x^2$ . Hence, the area of a triangular slice is $\dfrac{1}{2}(x + 2 - x^2)^2$ . The volume is

$$V = \int_{-1}^2 \dfrac{1}{2}(x + 2 - x^2)^2\,dx = \dfrac{1}{2} \int_{-1}^2 \left(x^4 - 2 x^3 - 3 x^2 + 4 x + 4\right)\,dx =$$

$$\dfrac{1}{2} \left[\dfrac{1}{5}x^5 - \dfrac{1}{2}x^4 - x^3 + 2 x^2 + 4 x\right]_{-1}^2 = \dfrac{81}{20} = 4.05.\quad\halmos$$

8. The base of a solid is the region in the x-y-plane bounded above by the line $y = 1$ and below by the parabola $y = x^2$ . The cross-sections in planes perpendicular to the y-axis are squares having one edge in the x-y-plane. Find the volume of the solid.

$$\hbox{\epsfysize=2in \epsffile{rev2-12a.eps}} \hskip0.5in \hbox{\epsfysize=2in \epsffile{rev2-12b.eps}}$$

The first picture shows the base of the solid. The second picture shows three typical square slices standing on the base.

The thickness of a typical slice is in the y-direction, so I'll use y as my variable. Solving $y = x^2$ for x gives $x = \pm \sqrt{y}$ .

The side of a square slice extends from $x = -\sqrt{y}$ to $x = \sqrt{y}$ , so its length is $\sqrt{y} - (-\sqrt{y}) = 2 \sqrt{y}$ . The area of a typical square slice is $(2 \sqrt{y})^2 = 4 y$ . Hence, the volume is

$$\int_0^1 4 y\,dy = \left[2 y^2\right]_0^1 = 2.\quad\halmos$$

9. The region which lies above the x-axis and below the graph of $y = \dfrac{1}{x^2 + 1}$ , $-\infty < x < \infty$ , is revolved about the x-axis. Find the volume of the solid which is generated.

$$\hbox{\epsfysize=1.75in \epsffile{rev2-10.eps}}$$

Chop the solid up into circular slices perpendicular to the x-axis. The thickness of a typical slice is $dx$ . The radius of a slice is $r = \dfrac{1}{x^2 + 1}$ . The volume is

$$V = \int_{-\infty}^\infty \pi\cdot\dfrac{1}{(x^2 + 1)^2}\,dx = \int_0^\infty \pi\cdot\dfrac{1}{(x^2 + 1)^2}\,dx + \int_{-\infty}^0 \pi\cdot\dfrac{1}{(x^2 + 1)^2}\,dx.$$

Compute the first integral:

$$\int_0^\infty \pi\cdot\dfrac{1}{(x^2 + 1)^2}\,dx = \lim_{a\to +\infty} \int_0^a \pi\cdot\dfrac{1}{(x^2 + 1)^2}\,dx = \pi\cdot\lim_{a\to +\infty} \left[\dfrac{1}{2}\dfrac{x}{x^2 + 1} + \dfrac{1}{2}\tan^{-1} x\right]_0^a =$$

$$\dfrac{\pi}{2}\lim_{a\to +\infty} \left(\dfrac{a}{a^2 + 1} + \tan^{-1} a\right) = \dfrac{\pi^2}{4}.$$

(I used the fact that $\lim_{a \to +\infty} \tan^{-1} a = \dfrac{\pi}{2}$ .)

Similarly,

$$\int_{-\infty}^0 \pi\cdot\dfrac{1}{(x^2 + 1)^2}\,dx = \dfrac{\pi^2}{4}.$$

The volume is $\dfrac{\pi^2}{4} + \dfrac{\pi^2}{4} = \dfrac{\pi^2}{2}$ .

10. A force of 8 pounds is required to extend a spring 2 feet beyond its unstretched length.

(a) Find the spring constant k.

(b) Find the work done in stretching the spring from 2 feet beyond its unstretched length to 3 feet beyond its unstretched length.

(a)

$$\eqalign{ F & = -k x \cr 8 & = -2 k \cr k & = -4 \quad\halmos \cr}$$

(b) Since $k = -4$ , I have $F = 4 x$ . Hence, the work done is

$$\int_2^3 4 x\,dx = \left[2 x^2\right]_2^3 = 10\ \hbox{foot-pounds}. \quad\halmos$$

11. The base of a rectangular tank is 2 feet long and 3 feet wide; the tank is 6 feet high. Find the work done in pumping all the water out of the top of the tank.

Divide the water up into rectangular slabs parallel to the base. Let y denote the height of a slab above the base.

$$\hbox{\epsfysize=1.5in \epsffile{rev2-11.eps}}$$

The volume of a typical slab is $(2)(3)\,dy = 6\,dy$ , so the weight is $62.4\cdot 6\,dy$ . (The density of water is 62.4 pounds per cubic foot.)

A slab at height y must be lifted a distance of $6 - y$ to get to the top of the tank. Therefore, the work done in lifting the slab is $62.4\cdot 6(6 - y)\,dy$ . The total work is

$$\int_0^6 62.4\cdot 6(6 - y)\,dy = 62.4\cdot 6\left[6 y - \dfrac{1}{2}y^2\right]_0^6 = 6739.2\ \hbox{foot-pounds}.\quad\halmos$$

12. Write a formula for the n-th term of the sequence, assuming that the terms continue in the "obvious" way.

(a) $7, 11, 15, 19, 23, 27, \ldots$ .

(b) $\dfrac{2}{8}, \dfrac{4}{13}, \dfrac{6}{18}, \dfrac{8}{23}, \ldots$ .

(a)

$$a_n = 7 + 4 n \quad\hbox{for}\quad n = 0, 1, 2, \ldots.\quad\halmos$$

(b)

$$a_n = \dfrac{2 n}{3 + 5 n} \quad\hbox{for}\quad n = 1, 2, 3, \ldots.\quad\halmos$$

13. A sequence is defined recursively by

$$a_{n + 1} = 3 a_n + 5 \quad\hbox{for}\quad n \ge 0 \quad\hbox{and}\quad a_0 = 1.$$

Write down the first 5 terms of the sequence.

$$a_0 = 1, \quad a_1 = 8, \quad a_2 = 29, \quad a_3 = 92, \quad a_4 = 281.\quad\halmos$$

14. Determine whether the sequence $a_n = \dfrac{e^n}{n + 1}$ for $n \ge 1$ eventually increases, decreases, or neither increases nor decreases.

Let $f(x) = \dfrac{e^x}{x + 1}$ . Then

$$f'(x) = \dfrac{(x + 1) e^x - e^x}{(x + 1)^2} = \dfrac{x e^x}{(x + 1)^2} > 0 \quad\hbox{for}\quad x \ge 1.$$

Hence, the sequence increases.

15. Determine whether the sequence $a_n = \cos (\pi n)$ for $n \ge 0$ eventually increases, decreases, or neither increases nor decreases.

The terms are

$$1,\ -1,\ 1,\ -1,\ \ldots.$$

In fact, $\cos (\pi n) = (-1)^n$ . Hence, the sequence neither increases nor decreases.

16. Is the following sequence bounded? Why or why not?

$$1,\ 1,\ 1,\ 2,\ 1,\ 3\, \ldots 1,\ n,\ \ldots .$$

The even-numbered terms have the form n for $n \ge 1$ , and $\displaystyle \lim_{n \to \infty} n = \infty$ . Hence, the sequence is not bounded.

17. Determine whether the sequence converges or diverges; if it converges, find the limit.

(a) $\displaystyle \left\{1.0001^n\right\}$

(b) $\displaystyle \left\{\dfrac{e^n + 3^n}{2^n + \pi^n}\right\}$

(c) $\displaystyle \left\{\dfrac{2 n^3 - 5 n + 7}{7 n^2 - 13 n^3}\right\}$

(d) $\displaystyle \left\{\left(\tan^{-1} n\right)^2\right\}$

(e) $\displaystyle \left\{\dfrac{\sin n}{n^2}\right\}$ .

(f) $\displaystyle \left\{\left(\dfrac{4 n + 1}{9 n + 17} + e^{-n^2}\right)^n\right\}$ .

(a) Since $\displaystyle \left\{1.0001^n\right\}$ is a geometric sequence with ratio $r = 1.0001 > 1$ ,

$$\lim_{n \to \infty} 1.0001^n = +\infty.\quad\halmos$$

(b) Divide the top and bottom by $\pi^n$ (since $\pi^n$ is the biggest exponential in the fraction):

$$\lim_{n \to \infty} \dfrac{e^n + 3^n}{2^n + \pi^n} = \lim_{n \to \infty} \dfrac{\dfrac{e^n}{pi^n} + \dfrac{3^n}{\pi^n}}{\dfrac{2^n}{\pi^n} + 1} = \dfrac{0 + 0}{0 + 1} = 0.$$

I computed the limit using the fact that the following are geometric sequences:

$$\dfrac{e^n}{pi^n} = \left(\dfrac{e}{\pi}\right)^n, \quad \dfrac{3^n}{\pi^n} = \left(\dfrac{3}{\pi}\right)^n, \quad\hbox{and}\quad \dfrac{2^n}{\pi^n} = \left(\dfrac{2}{\pi}\right)^n.$$

Their ratios are all less than 1, so they go to 0 as $n \to \infty$ .

(c)

$$\lim_{n \to \infty} \dfrac{2 n^3 - 5 n + 7}{7 n^2 - 13 n^3} = -\dfrac{2}{13}.$$

I did this by considering the highest powers on the top and bottom; they're both $x^3$ , so I just looked at their coefficients. You could also do this by using L'Hôpital's rule, or by dividing the top and the bottom by $x^3$ .

(d)

$$\lim_{n \to \infty} \left(\tan^{-1} n\right)^2 = \left(\lim_{n \to \infty} \tan^{-1} n\right)^2 = \left(\dfrac{\pi}{2}\right)^2 = \dfrac{\pi^2}{4}.\quad\halmos$$

(e) Note that $\displaystyle \lim_{n \to \infty} \sin n$ is undefined, so I can't take the limit of the terms directly. Instead, I'll use the Squeezing Theorem. I have

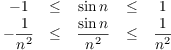
$$\matrix{ -1 & \le & \sin n & \le & 1 \cr \noalign{\vskip2 pt} -\dfrac{1}{n^2} & \le & \dfrac{\sin n}{n^2} & \le & \dfrac{1}{n^2} \cr}$$

Also,

$$\lim_{n \to \infty} -\dfrac{1}{n^2} = 0 \quad\hbox{and}\quad \lim_{n \to \infty} \dfrac{1}{n^2} = 0.$$

By the Squeezing Theorem, $\displaystyle \lim_{n \to \infty} \dfrac{\sin n}{n^2} = 0$ .

(f) Note that

$$\lim_{n \to \infty} \left(\dfrac{4 n + 1}{9 n + 17} + e^{-n^2}\right) = \dfrac{4}{9} + 0 = \dfrac{4}{9}.$$

Since $\lim_{n \to \infty} \left(\dfrac{4}{9}\right)^n = 0$ , it follows that

$$\lim_{n \to \infty} \left(\dfrac{4 n + 1}{9 n + 17} + e^{-n^2}\right)^n = 0.\quad\halmos$$

18. A sequence is defined recursively by

$$a_1 = 5, \quad a_{n+1} = \sqrt{6 a_n + 27} \quad\hbox{for}\quad n \ge 1.$$

Find $\displaystyle \lim_{n \to \infty} a_n$ .

Taking the limit on both sides of the recursion equation, I get

$$\lim_{n \to \infty} a_{n+1} = \lim_{n \to \infty} \sqrt{6 a_n + 27} = \sqrt{6 \lim_{n \to \infty} a_n + 27}.$$

I'm allowed to move the limit inside the square root by a standard rule for limits.

Now $\displaystyle \lim_{n \to \infty} a_{n+1} = \lim_{n \to \infty} a_n$ because both limits represent what the sequence $\{a_n\}$ is approaching. So let

$$L = \lim_{n \to \infty} a_{n+1} = \lim_{n \to \infty} a_n.$$

Then

$$\eqalign{ L & = \sqrt{6 L + 27} \cr L^2 & = 6 L + 27 \cr L^2 - 6 L - 27 & = 0 \cr (L - 9)(L + 3) & = 0 \cr L = 9 & \quad\hbox{or}\quad L = -3 \cr}$$

Since the sequence consists of positive numbers, it can't have a negative limit. This rules out -3. Therefore,

$$\lim_{n \to \infty} a_n = 9.\quad\halmos$$

19. If the series converges, find the exact value of its sum; if it diverges, explain why.

(a) $\displaystyle \sum_{n = 1}^\infty \left(-\dfrac{1}{5}\right)^n$ .

(b) $\displaystyle \sum_{n = 1}^\infty (-1.021)^n$ .

(c)

$$\dfrac{3}{5^3} + \dfrac{3}{5^4} + \dfrac{3}{5^5} + \cdots + \dfrac{3}{5^n} + \cdots.$$

(d) $\displaystyle \sum_{n = 2}^\infty \left(\dfrac{6^n}{7^n} + 2 \cdot \dfrac{(-1)^n}{4^n}\right)$ .

(e) $\displaystyle \sum_{n = 3}^\infty \left(\dfrac{5^n}{4^n} + \dfrac{4^n}{5^n}\right)$ .

(f) $\displaystyle \sum_{n = 3}^\infty \ln \dfrac{n}{n +1}$ .

(a) The series converges, and

$$\sum_{n = 1}^\infty \left(-\dfrac{1}{5}\right)^n = \dfrac{-\dfrac{1}{5}}{1 - \left(-\dfrac{1}{5}\right)} = -\dfrac{1}{6}.\quad\halmos$$

(b) Since the ratio -1.021 is not in the interval $(-1, 1]$ , the series diverges. In fact, it diverges by oscillation, as alternate partial sums approach $+\infty$ and $-\infty$ .

(c) The series converges, and

$$\dfrac{3}{5^3} + \dfrac{3}{5^4} + \dfrac{3}{5^5} + \cdots + \dfrac{3}{5^n} + \cdots = \dfrac{\dfrac{3}{5^3}}{1 - \dfrac{1}{5}} = \dfrac{3}{100}.\quad\halmos$$

(d) The series is the sum of two convergent geometric series, so it converges. First,

$$\sum_{n = 2}^\infty \dfrac{6^n}{7^n} = \dfrac{\dfrac{6^2}{7^2}}{1 - \dfrac{6}{7}} = \dfrac{36}{7}.$$

Next,

$$\sum_{n = 2}^\infty \dfrac{(-1)^n}{4^n} = \dfrac{\dfrac{1}{4^2}}{1 - \left(-\dfrac{1}{4}\right)} = \dfrac{1}{20}.$$

Hence,

$$\sum_{n = 2}^\infty \left(\dfrac{6^n}{7^n} + 2 \cdot \dfrac{(-1)^n}{4^n}\right) = \dfrac{36}{7} + 2 \cdot \dfrac{1}{20} = \dfrac{367}{70}.\quad\halmos$$

(e) The series $\displaystyle \sum_{n = 3}^\infty \dfrac{4^n}{5^n}$ is a convergent geometric series, but $\displaystyle \sum_{n = 3}^\infty \dfrac{5^n}{4^n}$ is a divergent geometric series, since the ratio $\dfrac{5}{4}$ is greater than 1. Hence, the given series diverges --- in fact, it diverges to $+\infty$ .

(f) Note that

$$\sum_{n = 3}^\infty \ln \dfrac{n}{n +1} = \sum_{n = 3}^\infty \left(\ln n - \ln (n + 1)\right).$$

Writing out the first few terms, you can see that the series converges by telescoping:

$$\sum_{n = 3}^\infty \left(\ln n - \ln (n + 1)\right) = \left(\ln 3 - \ln 4\right) + \left(\ln 4 - \ln 5\right) + \left(\ln 5 - \ln 6\right) + \cdots = \ln 3.\quad\halmos$$

20. (a) Find the partial fractions decomposition of $\dfrac{2}{(2 k + 1)(2 k + 3)}$ .

(b) Use (a) to find the sum of the series

$$\sum_{k = 1}^{\infty} \dfrac{2}{(2 k + 1)(2 k + 3)}.$$

(a)

$$\eqalign{ \dfrac{2}{(2 k + 1)(2 k + 3)} & = \dfrac{A}{2 k + 1} + \dfrac{B}{2 k + 3} \cr \noalign{\vskip2 pt} 2 & = A(2 k + 3) + B(2 k + 1) \cr}$$

Set $x = -\dfrac{1}{2}$ : I get $2 = 2 A$ , so $A = 1$ .

Set $x = -\dfrac{3}{2}$ : I get $2 = -2 B$ , so $B = -1$ .

Therefore,

$$\dfrac{2}{(2 k + 1)(2 k + 3)} = \dfrac{1}{2 k + 1} - \dfrac{1}{2 k + 3}.\quad\halmos$$

(b)

$$\sum_{k = 1}^{\infty} \dfrac{2}{(2 k + 1)(2 k + 3)} = \sum_{k = 1}^{\infty} \left(\dfrac{1}{2 k + 1} - \dfrac{1}{2 k + 3}\right) = \left(\dfrac{1}{3} - \dfrac{1}{5}\right) + \left(\dfrac{1}{5} - \dfrac{1}{7}\right) + \left(\dfrac{1}{7} - \dfrac{1}{9}\right) + \ldots.$$

The second fraction in each pair cancels with the first fraction in the next pair. The only one that isn't cancelled is the very first one: $\dfrac{1}{3}$ . Therefore,

$$\sum_{k = 1}^{\infty} \dfrac{2}{(2 k + 1)(2 k + 3)} = \dfrac{1}{3}.\quad\halmos$$

21. Find series $\displaystyle \sum_{n = 1}^\infty a_n$ and $\displaystyle \sum_{n = 1}^\infty b_n$ such that both series diverge, and:

(a) $\displaystyle \sum_{n = 1}^\infty (a_n + b_n)$ diverges.

(b) $\displaystyle \sum_{n = 1}^\infty (a_n + b_n)$ converges.

(a) Let $a_n = \dfrac{1}{n}$ and $b_n = \dfrac{1}{n}$ . Then $\displaystyle \sum_{n = 1}^\infty a_n = \sum_{n = 1}^\infty \dfrac{1}{n}$ and $\displaystyle \sum_{n = 1}^\infty b_n = \sum_{n = 1}^\infty \dfrac{1}{n}$ both diverge, because they're harmonic.

And $\displaystyle \sum_{n = 1}^\infty (a_n + b_n) = \sum_{n = 1}^\infty \dfrac{2}{n}$ diverges as well, since it's twice the harmonic series.

(b) Let $a_n = \dfrac{1}{n}$ and $b_n = -\dfrac{1}{n}$ . Then $\displaystyle \sum_{n = 1}^\infty a_n = \sum_{n = 1}^\infty \dfrac{1}{n}$ diverges because it's the harmonic series, and $\displaystyle \sum_{n = 1}^\infty b_n = \sum_{n = 1}^\infty -\dfrac{1}{n}$ diverges because it's the negative of the harmonic series.

However, $\displaystyle \sum_{n = 1}^\infty (a_n + b_n) = \sum_{n = 1}^\infty 0$ converges, and its sum is 0.

This problem shows that the term-by-term sum of two divergent series can either converge or diverge.

22. Calvin Butterball notes that $\displaystyle \lim_{n \to \infty} \dfrac{1}{\sqrt{n}} = 0$ , and concludes that the series $\displaystyle \sum_{n = 1}^\infty \dfrac{1}{\sqrt{n}}$ converges by the Zero Limit Test. What's wrong with his reasoning?

The Zero Limit Test says that if the limit of the terms is not 0, then the series diverges. It does not say that if the limit of the terms is 0, then the series converges. (The second statement is called the converse of the first; the converse of a statement is not the same as, or equivalent to, the statement.)

In fact, $\displaystyle \sum_{n = 1}^\infty \dfrac{1}{\sqrt{n}}$ diverges, because it's a p-series with $p = \dfrac{1}{2} < 1$ .

23. If the series $\displaystyle \sum_{k = 17}^{\infty} a_k$ , converges, does the series $\displaystyle \sum_{k = 1}^{\infty} a_k$ converge?

If the series $\displaystyle \sum_{k = 17}^{\infty} a_k$ converges, then the series $\displaystyle \sum_{k = 1}^{\infty} a_k$ converges. They only differ in the first 16 terms, and a finite number of terms cannot affect the convergence or divergence of an infinite series.

24. Does the series $\displaystyle \sum_{k = 1}^\infty (-1)^{k+1} \dfrac{2 k + 1}{4 k + 3}$ converge?

The series alternates, but

$$\lim_{k \to \infty} \dfrac{2 k + 1}{4 k + 3} = \dfrac{1}{2}.$$

The $(-1)^{k+1}$ causes the terms to oscillate in sign, so

$$\lim_{k \to \infty} (-1)^{k+1} \dfrac{2 k + 1}{4 k + 3} \quad\hbox{is undefined}.$$

The series diverges by the Zero Limit Test.

25. Determine whether the series converges or diverges: $\displaystyle \sum_{k = 1}^{\infty} \dfrac{3^k + 2^k}{6^k}$ .

The series is the sum of two convergent geometric series; in fact, its sum is

$$\sum_{k = 1}^{\infty} \dfrac{3^k + 2^k}{6^k} = \sum_{k = 1}^{\infty} \dfrac{3^k}{6^k} + \sum_{k = 1}^{\infty} \dfrac{2^k}{6^k} = \sum_{k = 1}^{\infty} \left(\dfrac{1}{2}\right)^k + \sum_{k = 1}^{\infty} \left(\dfrac{1}{3}\right)^k = \dfrac{\dfrac{1}{2}}{1 - \dfrac{1}{2}} + \dfrac{\dfrac{1}{3}}{1 - \dfrac{1}{3}} = 1 + \dfrac{1}{2} = \dfrac{3}{2}.\quad\halmos$$

26. Determine whether the series converges or diverges:$\displaystyle \sum_{k = 3}^{\infty} \dfrac{k^2 - 3 k + 2}{k^4}$ .

$$\sum_{k = 3}^{\infty} \dfrac{k^2 - 3 k + 2}{k^4} = \sum_{k = 3}^{\infty} \dfrac{1}{k^2} - 3 \sum_{k = 3}^{\infty} \dfrac{1}{k^3} + 2 \sum_{k = 3}^{\infty} \dfrac{1}{k^4}.$$

The series on the right are convergent p-series. Hence, the original series converges.

27. Determine whether the series converges or diverges: $\displaystyle \sum_{k = 1}^{\infty} \sqrt{\tan^{-1} k}$ .

Note that

$$\lim_{k \to \infty} \sqrt{\tan^{-1} k} = \sqrt{\dfrac{\pi}{2}} \ne 0.$$

Hence, the series diverges by the Zero Limit Test.

28. Determine whether the series converges or diverges: $\displaystyle \sum_{k = 1}^{\infty} \dfrac{1}{k^{1.05}}$ .

Since $1.05 > 1$ , the series is a convergent p-series.

29. Determine whether the series converges or diverges: $\displaystyle \sum_{k=2}^{\infty} \dfrac{1}{k (\ln k)^2}$ .

Let $f(x) = \dfrac{1}{x (\ln x)^2}$ . It is positive and continuous for $x \ge 2$ . The derivative is

$$f'(x) = \dfrac{-2}{x^2 (\ln x)^3} - \dfrac{1}{x^2 (\ln x)^2}.$$

$f'(x) < 0$ for $x \ge 2$ , so f decreases for $x \ge 2$ . The hypotheses of the Integral Test are satisfied. Compute the integral:

$$\int_2^{\infty} \dfrac{1}{x (\ln x)^2}\,dx = \lim_{p \to \infty} \left[-\dfrac{1}{\ln x}\right]_2^p = \lim_{p \to \infty} \left(-\dfrac{1}{\ln p} + \dfrac{1}{\ln 2}\right) = \dfrac{1}{\ln 2}.$$

Since the integral converges, the series converges by the Integral Test.

30. Determine whether the series converges or diverges: $\displaystyle \sum_{k = 1}^{\infty} \dfrac{2}{3 k + 5}$ .

Let $f(x) = \dfrac{2}{3 x + 5}$ . Then f is positive and continuous for $x \ge 1$ . The derivative is

$$f'(x) = \dfrac{-6}{(3 x + 5)^2}.$$

$f'(x) < 0$ for $x \ge 1$ , so f decreases for $x \ge 1$ . The hypotheses of the Integral Test are satisfied. Compute the integral:

$$\int_1^{\infty} \dfrac{2}{3 x + 5}\,dx = \lim_{p \to \infty} \left[\dfrac{2}{3} \ln |3 x + 5|\right]_1^p = \dfrac{2}{3} \lim_{p \to \infty} \left(\ln |3 p + 5| - \ln 8\right) = +\infty.$$

The limit diverges, so the integral diverges. Therefore, the series diverges, by the Integral Test.

31. Determine whether the series converges or diverges: $\displaystyle \sum_{k = 1}^{\infty} \dfrac{e^x}{e^{2 x} + 1}$ .

The terms are positive, and $f(x) = \dfrac{e^x}{e^{2 x} + 1}$ is continuous for all x.

$$f'(x) = \dfrac{(e^{2 x} + 1)(e^x) - (e^x)(2 e^{2 x})}{(e^{2 x} + 1)^2} = \dfrac{e^x - e^{3 x}}{(e^{2 x} + 1)^2} = \dfrac{e^x(1 - e^{2 x})}{(e^{2 x} + 1)^2} < 0 \quad\hbox{for}\quad x \ge 1.$$

Hence, the terms decrease.

$$\int_1^\infty \dfrac{e^x}{e^{2 x} + 1}\,dx = \lim_{b \to \infty} \int_1^b \dfrac{e^x}{e^{2 x} + 1}\,dx = \lim_{b \to \infty} \int_e^{e^b} \dfrac{1}{u^2 + 1}\,du =$$

$$\left[u = e^x, \quad du = e^x\,dx, \quad dx = \dfrac{du}{e^x}; \quad x = 1, \quad u = e; \quad x = b, \quad u = e^b\right]$$

$$\lim_{b \to \infty} \left[\tan^{-1} u\right]_e^{e^b} = \lim_{b \to \infty} \left(\tan^{-1} e^b - \tan^{-1} e\right) = \dfrac{\pi}{2} - \tan^{-1} e.$$

The integral converges, so the series converges by the Integral Test.

He who has overcome his fears will truly be free. - Aristotle

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga