Review Problems for Test 3

Math 211

These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the absence of a topic does not imply that it won't appear on the test.

1. In each case, determine whether the series converges or diverges. You should cite the test you're using by name (to avoid ambiguity); be sure you verify that the hypotheses of the test apply. Any limits should be computed exactly and completely.

(a) $\displaystyle \sum_{k = 2}^{\infty} \dfrac{2}{k^2 - 1}$ .

(b) $\displaystyle \sum_{k = 1}^{\infty} \left(\dfrac{k + 1}{k^2 + 2}\right)^2$ .

(d) $\displaystyle \sum_{k = 1}^{\infty} \dfrac{2^k}{3^k + 2}$ .

(e) $\displaystyle \sum_{i=1}^{\infty} \dfrac{3^i}{i^3}$ .

(f) $\displaystyle \sum_{k = 1}^{\infty} \left(\dfrac{2 k + 2}{2 k - 1}\right)^{k^2}$ .

(g) $\displaystyle \sum_{k = 1}^{\infty} \dfrac{(k!)^2}{(2 k + 1)!}$ .

(h) $\displaystyle \sum_{n = 2}^\infty \left(1 - \dfrac{5}{n}\right)^{2 n^2}$ .

(i) $\displaystyle \sum_{n = 3}^\infty \dfrac{5 + 3 \sin n}{\sqrt{n - 1}}$ .

(j) $\displaystyle \sum_{n = 2}^\infty \dfrac{n! (2 n + 1)!}{(3 n)!}$ .

2. Show that the Ratio Test always fails for a p-series

$\sum_{k = 1}^{\infty} \dfrac{1}{k^p}, \quad\hbox{where}\quad p > 0.$

3. (a) Use the Alternating Series Test to show that the series $\displaystyle \sum_{k = 2}^{\infty} (-1)^k \dfrac{1}{\ln k}$ converges.

(b) Estimate the error incurred in using $\displaystyle \sum_{k = 2}^{100} (-1)^k \dfrac{1}{\ln k}$ to approximate the sum of the series.

4. What is the smallest number of terms of the series $\displaystyle \sum_{n = 1}^\infty \dfrac{(-1)^{n+1}}{4 \sqrt{n} + 5}$ needed to estimate the sum with an error of no more than $10^{-4}$ ?

5. What is the smallest value of n for which $\displaystyle \sum_{k = 2}^n \dfrac{(-1)^k 3^k}{k!}$ approximates the actual sum $\displaystyle \sum_{k = 2}^\infty \dfrac{(-1)^k 3^k}{k!}$ with an error of no more than $10^{-3}$ ?

6. Determine whether the series $\displaystyle \sum_{k = 1}^{\infty} (-1)^{k+1} \dfrac{k^3}{3^k}$ converges absolutely, converges conditionally, or diverges.

7. Determine whether the series $\displaystyle \sum_{k = 1}^{\infty} \dfrac{1}{1 - e^{-k}}$ converges absolutely, converges conditionally, or diverges.

8. Determine whether the series $\displaystyle \sum_{k = 2}^{\infty} (-1)^k \dfrac{1}{\root 3 \of k(\root 3 \of {k - 1})}$ converges absolutely, converges conditionally, or diverges.

9. Does the following series converge or diverge?

$\sum_{k = 1}^{\infty} \dfrac{\sin k \cos k}{k^2 + 1}$

10. Does the following series converge or diverge?

$\sum_{k = 1}^{\infty} \dfrac{\cos 3^k}{k^{3/2}}$

11. Determine the interval of convergence for the power series $\displaystyle \sum_{n = 1}^{\infty} \dfrac{2^n}{n!} (x + 5)^n$ .

12. Determine the interval of convergence for the power series $\displaystyle \sum_{n = 0}^{\infty} (-1)^n \dfrac{x^{2 n}}{(n!)^2 2^{2 n}}$ .

13. Determine the interval of convergence for the power series $\displaystyle \sum_{n = 1}^{\infty} (nx)^n$ .

14. Determine the interval of convergence for the power series $\displaystyle \sum_{n = 1}^{\infty} (-1)^{n+1} \dfrac{x^n}{\sqrt{n} 2^n}$ .

15. Determine the interval of convergence for the power series $\displaystyle \sum_{n = 0}^\infty \dfrac{n^2 (x - 3)^n}{5^n}$ .

16. Find the Taylor series at for $f(x) = \dfrac{3}{7 - 2 x}$ , and find its interval of convergence.

17. Find the Taylor series at for $f(x) = \dfrac{1}{8 + 3 x}$ , and find its interval of convergence.

18. Find the Taylor series at for $f(x) = e^{-3 x}$ , and find its interval of convergence.

19. The angle addition formula for cosine is

$\cos (a + b) = \cos a \cos b - \sin a \sin b.$

Use this formula to find the Taylor series for $\cos x$ expanded at .

20. (a) Find the Taylor series at for $\dfrac{1}{10 - x}$ .

(b) Find the Taylor series at for $f(x) = \dfrac{1}{(10 - x)^2}$ by differentiating the series in (a).

21. (a) Find the Taylor series at for $\dfrac{1}{1 + x^4}$ .

(b) Find the Taylor series at for $f(x) = \dfrac{x^3}{(1 + x^4)^2}$ by differentiating the series in (a).

22. Suppose that

$f(1) = 5, \quad f'(1) = 2, \quad f''(1) = -2, \quad f^{(3)}(1) = 3.$

Use the $3^{\rm rd}$ degree Taylor polynomial to approximate .

23. Find the Taylor series at for $f(x) = \dfrac{e^x}{e^x + 1}$ up to the term of degree 2.

24. The first four terms of the Taylor series at for $f(t) = \sec t \tan t$ are

$\sec t \tan t = t + \dfrac{5}{6} t^3 + \dfrac{61}{120} t^5 + \dfrac{277}{1008} t^7 + \cdots.$

Find the first five terms of the Taylor series for $\sec x$ at .

25. If $f(x) = \sin x^3$ , what is $f^{(600)}(0)$ ?

26. Estimate the error made in using the $3^{\rm rd}$ degree Taylor polynomial to approximate if $0 \le x \le 0.5$ .

27. How large an interval about $\dfrac{\pi}{3}$ may be taken if the values of $\cos x$ are to be approximated using the first three terms of the Taylor series at $a = \dfrac{\pi}{3}$ and if the error is to be no greater than 0.0001 ?

28. Suppose $0 \le x \le 0.2$ . What is the smallest value of n for which the $n^{\rm th}$ degree Taylor polynomial of $f(x) = e^{-3 x}$ at approximates to an accuracy of at least $10^{-6}$ ?

29. (a) Find the Taylor series for $\dfrac{\ln (1 + x^2)}{x}$ at .

(b) Express the series using summation notation.

(c) Calvin Butterball is bothered by parts (a) and (b). "How can you define the Taylor series for $f(x) = \dfrac{\ln (1 + x^2)}{x}$ when $\dfrac{\ln (1 + x^2)}{x}$ isn't defined at ?", he whines.

Actually, he has a valid point. Use the series of part (a) to compute

$\lim_{x \to 0} \dfrac{\ln (1 + x^2)}{x}.$

Then use the result to redefine f so that it's at least continuous at .

(d) Find $f^{(91)}(0)$ .

(e) Use the series of part (a) to approximate the following integral to within 0.01:

$\int_0^1 \dfrac{\ln (1 + x^2)}{x}\,dx$

Justify the accuracy of your approximation using the error estimate for alternating series.

30. Find parametric equations for the curve .

31. Find parametric equations for the curve .

32. Find parametric equations for the segment from to . Find a parameter range for which the segment is traced out exactly once.

33. Find parametric equations for the circle with center and radius 2.

34. Find an x-y equation for the curve whose parametric equations are

$x = t + 2, \quad y = t^2 + 5.$

35. Find an x-y equation for the curve whose parametric equations are

$x = 2 \cos t + 6, \quad y = 3 \sin t + 5.$

36. and $y = e^{2 t} + 1$ is a parametrization of part of the curve , but it does not represent the whole curve. Why not?

37. Find the value(s) of t for which the following curve has horizontal tangents, and the value(s) for which it has vertical tangents:

$x = (t + 1)^2, \quad y = t^3 - 6 t^2 - 36 t + 5.$

38. Find the points at which the following parametric curves intersect:

$\left\{\matrix{x = s \cr y = s^2 + s + 1 \cr}\right. \quad\hbox{and}\quad \left\{\matrix{x = t + 1 \cr y = 2 t + 5 \cr}\right.$

39. Consider the parametric curve

$x = t^2 + t + 1, \quad y = t^3 - 5 t + 2.$

(a) Find the equation of the tangent line at .

(b) Find $\dfrac{d^2 y}{dx^2}$ at .

40. Find $\dfrac{d^2 y}{dx^2}$ at for the parametric curve

$x = t^2 + 2 t + 2, \quad y = t^3 + 1.$

Solutions to the Review Problems for Test 3

(a) $\displaystyle \sum_{k = 2}^{\infty} \dfrac{2}{k^2 - 1}$ .

(b) $\displaystyle \sum_{k = 1}^{\infty} \left(\dfrac{k + 1}{k^2 + 2}\right)^2$ .

(d) $\displaystyle \sum_{k = 1}^{\infty} \dfrac{2^k}{3^k + 2}$ .

(e) $\displaystyle \sum_{i=1}^{\infty} \dfrac{3^i}{i^3}$ .

(f) $\displaystyle \sum_{k = 1}^{\infty} \left(\dfrac{2 k + 2}{2 k - 1}\right)^{k^2}$ .

(g) $\displaystyle \sum_{k = 1}^{\infty} \dfrac{(k!)^2}{(2 k + 1)!}$ .

(h) $\displaystyle \sum_{n = 2}^\infty \left(1 - \dfrac{5}{n}\right)^{2 n^2}$ .

(i) $\displaystyle \sum_{n = 3}^\infty \dfrac{5 + 3 \sin n}{\sqrt{n - 1}}$ .

(j) $\displaystyle \sum_{n = 2}^\infty \dfrac{n! (2 n + 1)!}{(3 n)!}$ .

(a)

$\lim_{k \to \infty} \dfrac{\dfrac{2}{k^2 - 1}}{\dfrac{1}{k^2}} = \lim_{k \to \infty} \dfrac{2 k^2}{k^2 - 1} = 2.$

The limit is a finite positive number. $\displaystyle \sum_{k = 2}^{\infty} \dfrac{1}{k^2}$ converges, because it's a p-series with . Therefore, $\displaystyle \sum_{k = 2}^{\infty} \dfrac{2}{k^2 - 1}$ converges by Limit Comparison.

(b) Rewrite the series as

$\sum_{k = 1}^{\infty} \dfrac{(k + 1)^2}{(k^2 + 2)^2}.$

For large k,

$\dfrac{(k + 1)^2}{(k^2 + 2)^2} \approx \dfrac{k^2}{k^4} = \dfrac{1}{k^2}.$

Use Limit Comparison with the series $\displaystyle \sum_{k = 1}^{\infty} \dfrac{1}{k^2}$ . The limiting ratio is

$\lim_{k \to \infty} \dfrac{\dfrac{(k + 1)^2}{(k^2 + 2)^2}}{\dfrac{1}{k^2}} = \lim_{k \to \infty} \dfrac{k^2 (k + 1)^2}{(k^2 + 2)^2} = 1.$

The limit is finite and positive. Since $\displaystyle \sum_{k = 1}^{\infty} \dfrac{1}{k^2}$ is a convergent p-series ( ), the series converges by Limit Comparison.

(c) I'll use Limit Comparison with $\displaystyle \sum_{k = 1}^{\infty} \dfrac{1}{k^2}$ . Rationale: For $\theta \approx 0$ , $\sin \theta \approx \theta$ , so $\left(\sin \dfrac{1}{k}\right)^2 \approx \dfrac{1}{k^2}$ .

$\lim_{k \to \infty} \dfrac{\left(\sin \dfrac{1}{k}\right)^2} {\dfrac{1}{k^2}} = \left(\lim_{k \to \infty} \dfrac{\sin \dfrac{1}{k}} {\dfrac{1}{k}}\right)^2 = \left(\lim_{m \to 0} \dfrac{\sin m}{m}\right)^2 = 1.$

(I set $m = \dfrac{1}{k}$ . As $k \to \infty$ , $m \to 0$ .)

The limit is a finite, positive number, and the series $\displaystyle \sum_{k = 1}^{\infty} \dfrac{1}{k^2}$ is a convergent p-series ( ). Therefore, the series converges, by Limit Comparison.

(d) Since making the bottom of a fraction smaller makes the fraction larger,

$\dfrac{2^k}{3^k + 2} < \dfrac{2^k}{3^k}.$

The series $\displaystyle \sum_{k = 1}^{\infty} \dfrac{2^k}{3^k}$ is geometric with ratio $r = \dfrac{2}{3}$ , so it converges. Therefore, the series $\displaystyle \sum_{k = 1}^{\infty} \dfrac{2^k}{3^k + 2}$ converges by direct comparison.

(e) Apply the Ratio Test:

$\lim_{i \to \infty} \dfrac{a_{i+1}}{a_i} = \lim_{i \to \infty} \dfrac{\dfrac{3^{i+1}}{(i+1)^3}} {\dfrac{3^i}{i^3}} = \lim_{i \to \infty} \dfrac{3^{i+1}}{3^i} \cdot \dfrac{i^3}{(i+1)^3} = \lim_{i \to \infty} 3 \cdot \left(\dfrac{i}{i+1}\right)^3 = 3.$

Since the limit is larger than 1, the series diverges by the Ratio Test.

(f) The $k^{\rm th}$ root of the $k^{\rm th}$ term is

$a_k^{1/k} = \left(\dfrac{2 k + 2}{2 k - 1}\right)^k.$

To compute the limit as $k \to \infty$ , let $y = \left(\dfrac{2 k + 2}{2 k - 1}\right)^k$ . Then

$\ln y = \ln \left(\dfrac{2 k + 2}{2 k - 1}\right)^k = k \ln \dfrac{2 k + 2}{2 k - 1}.$

Therefore,

$\lim_{k \to \infty} \ln y = \lim_{k \to \infty} k \ln \dfrac{2 k + 2}{2 k - 1} = \lim_{k \to \infty} \dfrac{\ln \dfrac{2 k + 2}{2 k - 1}}{\dfrac{1}{k}} = \lim_{k \to \infty} \dfrac{\dfrac{2 k - 1}{2 k + 2}\cdot \dfrac{-6}{(2 k - 1)^2}} {\dfrac{-1}{k^2}} =$

$6 \lim_{k \to \infty} \dfrac{(2 k - 1)(k^2)}{(2 k + 2)(2 k - 1)^2} = \dfrac{6}{4} = \dfrac{3}{2}.$

Therefore, $\displaystyle \lim_{k \to \infty} y = e^{3/2}$ .

Since $e^{3/2} > 1$ , the series diverges by the Root Test.

(g) Apply the Ratio Test:

$\lim_{k \to \infty} \dfrac{a_{k+1}}{a_k} = \lim_{k \to \infty} \dfrac{\dfrac{((k+1)!)^2}{(2 k + 3)!}} {\dfrac{(k!)^2}{(2 k + 1)!}} = \lim_{k \to \infty} \left(\dfrac{(k+1)!}{k!}\right)^2\cdot \dfrac{(2 k + 1)!}{(2 k + 3)!} = \lim_{k \to \infty} \dfrac{(k + 1)^2}{(2 k + 2)(2 k + 3)} = \dfrac{1}{4}.$

Since the limit is less than 1, the series converges by the Ratio Test.

(h) Apply the Root Test and compute the limit:

$\lim_{n \to \infty} \left[\left(1 - \dfrac{5}{n}\right)^{2 n^2}\right]^{1/n} = \lim_{n \to \infty} \left(1 - \dfrac{5}{n}\right)^{2 n}.$

Then

$\eqalign{ y & = \left(1 - \dfrac{5}{n}\right)^{2 n} \cr \ln y & = 2 n \ln \left(1 - \dfrac{5}{n}\right) \cr}$

$\lim_{n \to \infty} 2 n \ln \left(1 - \dfrac{5}{n}\right) = 2 \lim_{n \to \infty} \dfrac{\ln \left(1 - \dfrac{5}{n}\right)} {\dfrac{1}{n}} = 2 \lim_{n \to \infty} \dfrac{\left(\dfrac{1}{1 - \dfrac{5}{n}}\right) \left(\dfrac{5}{n^2}\right)} {\left(-\dfrac{1}{n^2}\right)} = -10 \lim_{n \to \infty} \dfrac{1}{1 - \dfrac{5}{n}} = -10.$

Hence,

$\lim_{n \to \infty} \left(1 - \dfrac{5}{n}\right)^{2 n} = e^{-10} < 1.$

The series converges by the Root Test.

(i) I have

$\eqalign{ -1 \le\ & \sin n \le 1 \cr -3 \le\ & 3 \sin n \le 3 \cr 5 + (-3) \le\ & 5 + 3 \sin n \le 5 + 3 \cr 2 \le\ & 5 + 3 \sin n \le 8 \cr}$

Then taking the first " $\le$ " and dividing by $\sqrt{n - 1}$ , I have

$\dfrac{2}{\sqrt{n - 1}} \le \dfrac{5 + 3 \sin n}{\sqrt{n - 1}}.$

If I replace the " " in the bottom on the left with "n", I'm adding 1, which makes the bottom bigger. This makes the fraction smaller. So

$\dfrac{2}{\sqrt{n}} < \dfrac{2}{\sqrt{n - 1}} \le \dfrac{5 + 3 \sin n}{\sqrt{n - 1}}.$

$\displaystyle \sum_{n = 3}^\infty \dfrac{2}{\sqrt{n}}$ is 2 times a p-series with $p = \dfrac{1}{2} < 1$ , so it diverges. Therefore, the original series diverges by direct comparison.

Question: How would this problem change if the original series had been $\displaystyle \sum_{n = 3}^\infty \dfrac{5 + 3 \sin n}{n^{3/2}}$ ? Work it out for yourself.

(j) Use the Ratio Test:

$\lim_{n \to \infty} \dfrac{\dfrac{(n + 1)! (2 n + 3)!}{(3 n + 3)!}} {\dfrac{n! (2 n + 1)!}{(3 n)!}} = \lim_{n \to \infty} \dfrac{(n + 1)!}{n!} \cdot \dfrac{(2 n + 3)!}{(2 n + 1)!} \cdot \dfrac{(3 n)!}{(3 n + 3)!} = \lim_{n \to \infty} \dfrac{(n + 1)(2 n + 2)(2 n + 3)}{(3 n + 1)(3 n + 2)(3 n + 3)} = \dfrac{4}{27} < 1.$

The series converges by the Ratio Test.

Here's how I simplified the factorial expressions:

$\dfrac{(n + 1)!}{n!} = \dfrac{1 \cdot 2 \cdot 3 \cdots n(n + 1)}{1 \cdot 2 \cdot 3 \cdots n} = n + 1.$

$\dfrac{(2 n + 3)!}{(2 n + 1)!} = \dfrac{1 \cdot 2 \cdot 3 \cdots (2 n + 1)(2 n + 2)(2 n + 3)} {1 \cdot 2 \cdot 3 \cdots (2 n + 1)} = (2 n + 2)(2 n + 3).$

$\dfrac{(3 n)!}{(3 n + 3)!} = \dfrac{1 \cdot 2 \cdot 3 \cdots (3 n)} {1 \cdot 2 \cdot 3 \cdots (3 n)(3 n + 1)(3 n + 2)(3 n + 3)} = \dfrac{1}{(3 n + 1)(3 n + 2)(3 n + 3)}.\quad\halmos$

2. Show that the Ratio Test always fails for a p-series

$\sum_{k = 1}^{\infty} \dfrac{1}{k^p}, \quad\hbox{where}\quad p > 0.$

The ratio of successive terms is

$\lim_{k \to \infty} \dfrac{a_{k+1}}{a_k} = \lim_{k \to \infty} \dfrac{\dfrac{1}{(k+1)^p}}{\dfrac{1}{k^p}} = \lim_{k \to \infty} \left(\dfrac{k}{k + 1}\right)^p = 1.$

Since the limit is 1, the Ratio Test fails.

Remark. This problem also shows that it's useless to apply the Ratio Test to series where the k-th term is a rational function of k.

For example, it's useless to apply the Ratio Test to

$\sum_{k = 1}^{\infty} \dfrac{k^2 + 5}{k^4 + 3}.$

For large k, $\dfrac{k^2 + 5}{k^4 + 3} \approx \dfrac{1}{k^2}$ , and the series is essentially a p-series.

3. (a) Use the Alternating Series Test to show that the series $\displaystyle \sum_{k = 2}^{\infty} (-1)^k \dfrac{1}{\ln k}$ converges.

(b) Estimate the error incurred in using $\displaystyle \sum_{k = 2}^{100} (-1)^k \dfrac{1}{\ln k}$ to approximate the sum of the series.

(a) The series clearly alternates, and

$\lim_{k \to\infty} \dfrac{1}{\ln k} = 0.$

Let $f(k) = \dfrac{1}{\ln k}$ . Then $f'(k) = -\dfrac{1}{k (\ln k)^2}$ , so for $k \ge 2$ . Hence, the terms of the series decrease in absolute value. By the Alternating Series Test, the series converges.

(b) If you use $\displaystyle \sum_{k = 2}^{100} (-1)^k \dfrac{1}{\ln k}$ to approximate the sum of the series, the error is no greater than (the absolute value of) the next term:

$\hbox{error} < \dfrac{1}{\ln 101} \approx 0.216679.\quad\halmos$

(c)

$\sum_{k = 2}^{6} (-1)^k \dfrac{1}{\ln k} \approx 1.19058 \quad\hbox{and}\quad \sum_{k = 2}^{7} (-1)^k \dfrac{1}{\ln k} \approx 0.67668.$

The actual sum s is caught between the consecutive partial sums: .

4. What is the smallest number of terms of the series $\displaystyle \sum_{n = 1}^\infty \dfrac{(-1)^{n+1}}{4 \sqrt{n} + 5}$ needed to estimate the sum with an error of no more than $10^{-4}$ ?

You can check that the series converges by the Alternating Series Test.

Hence, the error in using $\displaystyle \sum_{n = 1}^k \dfrac{(-1)^{n+1}}{4 \sqrt{n} + 5}$ to estimate the sum is less than the absolute value of the $(k + 1)^{rm st}$ term. So I want

$\eqalign{ \dfrac{1}{4 \sqrt{k + 1} + 5} & < 0.0001 \cr \noalign{\vskip2 pt} 1 & < 0.0001(4 \sqrt{k + 1} + 5) \cr \noalign{\vskip2 pt} \dfrac{1}{0.0001} & < 4 \sqrt{k + 1} + 5 \cr \noalign{\vskip2 pt} 10000 & < 4 \sqrt{k + 1} + 5 \cr 9995 & < 4 \sqrt{k + 1} \cr \noalign{\vskip2 pt} \dfrac{9995}{4} & < \sqrt{k + 1} \cr \noalign{\vskip2 pt} \left(\dfrac{9995}{4}\right)^2 & < k + 1 \cr \noalign{\vskip2 pt} 6243750.5625 < & k \cr}$

Thus, k is the next largest integer, and .

I have

$\left|\sum_{k = 2}^n \dfrac{(-1)^k 3^k}{k!} - (\hbox{actual sum})\right| < \dfrac{3^{n + 1}}{(n + 1)!}.$

Hence, I want the smallest n for which

$\dfrac{3^{n + 1}}{(n + 1)!} < 10^{-3}.$

I can't solve this inequality algebraically, so I have to use trial and error.

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & n & & $\dfrac{3^{n + 1}}{(n + 1)!}$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1 & & 4.5 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 2 & & 4.5 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 3 & & 3.375 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 4 & & 2.025 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 5 & & 1.0125 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 6 & & $0.43392 \ldots$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 7 & & $0.16272 \ldots$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 8 & & $0.05424 \ldots$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 9 & & $0.01627 \ldots$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 10 & & $0.00443 \ldots$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 11 & & $0.00110 \ldots$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 12 & & $2.56033 \ldots \cdot 10^{-4}$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }}$

The first n for which the inequality holds is .

6. Determine whether the series $\displaystyle \sum_{k = 1}^{\infty} (-1)^{k+1} \dfrac{k^3}{3^k}$ converges absolutely, converges conditionally, or diverges.

Consider the the absolute value series $\displaystyle \sum_{k = 1}^{\infty} \dfrac{k^3}{3^k}$ . Apply the Ratio Test:

$\lim_{k \to \infty} \dfrac{a_{k+1}}{a_k} = \lim_{k \to \infty} \dfrac{\dfrac{(k+1)^3}{3^{k+1}}} {\dfrac{k^3}{3^k}} = \lim_{k \to \infty} \left(\dfrac{k+1}{k}\right)^3\cdot \dfrac{3^k}{3^{k+1}} = \lim_{k \to \infty} \dfrac{1}{3} \left(\dfrac{k+1}{k}\right)^3 = \dfrac{1}{3} < 1.$

The series converges by the Ratio Test. Therefore, the original series converges absolutely.

7. Determine whether the series $\displaystyle \sum_{k = 1}^{\infty} \dfrac{1}{1 - e^{-k}}$ converges absolutely, converges conditionally, or diverges.

$\lim_{k \to \infty} \dfrac{1}{1 - e^{-k}} = 1 \ne 0.$

Hence, the series diverges, by the Zero Limit Test.

8. Determine whether the series $\displaystyle \sum_{k = 2}^{\infty} (-1)^k \dfrac{1}{\root 3 \of k(\root 3 \of {k - 1})}$ converges absolutely, converges conditionally, or diverges.

Consider the absolute value series $\displaystyle \sum_{k = 2}^{\infty} \dfrac{1}{\root 3 \of k(\root 3 \of {k - 1})}$ . Then

$\dfrac{1}{\root 3 \of k(\root 3 \of {k - 1})} > \dfrac{1}{(\root 3 \of k)(\root 3 \of k)} = \dfrac{1}{k^{2/3}}.$

The series $\displaystyle \sum_{k = 2}^{\infty} \dfrac{1}{k^{2/3}}$ is a divergent p-series ( $p = \dfrac{2}{3} < 1$ ). Therefore, the series $\sum_{k = 2}^{\infty} \dfrac{1}{\root 3 \of k(\root 3 \of {k - 1})}$ diverges by comparison, and the original series does not converge absolutely.

Go back to the original series $\displaystyle \sum_{k = 2}^{\infty} (-1)^k \dfrac{1}{(\root 3 \of k)(\root 3 \of {k - 1})}$ . The series clearly alternates, and

$\lim_{k \to \infty} \dfrac{1}{(\root 3 \of k)(\root 3 \of {k - 1})} = 0.$

Let $f(k) = \dfrac{1}{(\root 3 \of k)(\root 3 \of {k - 1})}$ . Then

$f'(k) = \dfrac{1}{3 k^{4/3} (k^{1/3} - 1)} - \dfrac{1}{3 k (k^{1/3} - 1)^2}.$

Since for $k \ge 2$ , the terms decrease in absolute value. Therefore, the series converges, by the Alternating Series Rule. Since the series did not converge absolutely, it converges conditionally.

9. Does the following series converge or diverge?

$\sum_{k = 1}^{\infty} \dfrac{\sin k \cos k}{k^2 + 1}$

Consider the absolute value series $\displaystyle \sum_{k = 1}^{\infty} \left| \dfrac{\sin k \cos k}{k^2 + 1} \right|$ . Since $\sin k \cos k = \dfrac{1}{2} \sin 2 k$ ,

$\left| \dfrac{\sin k \cos k}{k^2 + 1} \right| = \dfrac{1}{2} \left| \dfrac{\sin 2 k}{k^2 + 1} \right| \le \dfrac{1}{2} \dfrac{|\sin 2 k|}{k^2 + 1} \le \dfrac{1}{2} \dfrac{1}{k^2 + 1} < \dfrac{1}{2} \dfrac{1}{k^2}.$

The series $\displaystyle \sum_{k = 1}^{\infty} \dfrac{1}{2} \dfrac{1}{k^2}$ is a convergent p-series ( ). Therefore, the absolute value series converges by comparison. Hence, the original series converges absolutely. Therefore, the original series converges.

10. Does the following series converge or diverge?

$\sum_{k = 1}^{\infty} \dfrac{\cos 3^k}{k^{3/2}}$

You might think of applying the Alternating Series Rule, which allows us to handle series with negative terms. Unfortunately, the terms of this series do not alternate in sign; the signs of the first few terms are -, -, -, +, -, +, +, +, -, ... and no pattern ever emerges.

Instead, consider the absolute value series $\displaystyle \sum_{k = 1}^{\infty} \dfrac{|\cos 3^k|}{k^{3/2}}$ . Since $|\cos 3^k| \le 1$ ,

$\left|\dfrac{\cos 3^k}{k^{3/2}}\right| \le \dfrac{1}{k^{3/2}}.$

The series $\displaystyle \sum_{k = 1}^{\infty} \dfrac{1}{k^{3/2}}$ is a convergent p-series ( $p = \dfrac{3}{2}$ ). Therefore, the absolute value series $\displaystyle \sum_{k = 1}^{\infty} \left|\dfrac{\cos 3^k}{k^{3/2}}\right|$ converges by comparison. (The comparison test applies, because the absolute value series has positive terms!) Hence, the original series $\displaystyle \sum_{k = 1}^{\infty} \dfrac{\cos 3^k}{k^{3/2}}$ converges absolutely. Since absolute convergence implies convergence, the series converges.

11. Determine the interval of convergence for the power series $\displaystyle \sum_{n = 1}^{\infty} \dfrac{2^n}{n!} (x + 5)^n$ .

Apply the Ratio Test to the absolute value series:

$\lim_{n \to \infty} \dfrac{|a_{n+1}|}{|a_n|} = \lim_{n \to \infty} \dfrac{\dfrac{2^{n+1}}{(n + 1)!} |x + 5|^{n+1}} {\dfrac{2^n}{n!} |x + 5|^n} = \lim_{n \to \infty} \dfrac{2^{n+1}}{2^n} \dfrac{n!}{(n + 1)!} \dfrac{|x + 5|^{n+1}}{|x + 5|^n} = \lim_{n \to \infty} \dfrac{2}{n + 1} |x + 5| = 0.$

Since the limit is less than 1 independent of x, the series converges for all x.

12. Determine the interval of convergence for the power series $\displaystyle \sum_{n = 0}^{\infty} (-1)^n \dfrac{x^{2 n}}{(n!)^2 2^{2 n}}$ .

Apply the Ratio Test to the absolute value series:

$\lim_{n \to \infty} \dfrac{|a_{n+1}|}{|a_n|} = \lim_{n \to \infty} \dfrac{\dfrac{|x|^{2 n+2}}{((n+1)!)^2 2^{2 n+2}}} {\dfrac{|x|^{2 n}}{(n!)^2 2^{2 n}}} = \lim_{n \to \infty} \dfrac{2^{2 n}}{2^{2 n+2}}\cdot \left(\dfrac{n!}{(n + 1)!}\right)^2\cdot \dfrac{|x|^{2 n+2}}{|x|^{2 n}} = \lim_{n \to \infty} \dfrac{1}{4} \dfrac{1}{(n + 1)^2} |x|^2 = 0.$

Since the limit is less than 1 independent of x, the series converges (absolutely) for all values of x.

13. Determine the interval of convergence for the power series $\displaystyle \sum_{n = 1}^{\infty} (nx)^n$ .

Apply the Ratio Test to the absolute value series:

$\lim_{n \to \infty} \dfrac{|a_{n+1}|}{|a_n|} = \lim_{n \to \infty} \dfrac{(n + 1)^{n+1} |x|^{n+1}} {n^n |x|^n} = \lim_{n \to \infty} (n + 1)\cdot \left(\dfrac{n + 1}{n}\right)^n|x| = \lim_{n \to \infty} (n + 1)\cdot \left(1 + \dfrac{1}{n}\right)^n |x| = +\infty,$

(since $\displaystyle \lim_{n \to \infty} \left(1 + \dfrac{1}{n}\right)^n = e$ ).

Since the limit is greater than 1 independent of x, the series diverges for all x except . (A power series always converges at its point of expansion.)

14. Determine the interval of convergence for the power series $\displaystyle \sum_{n = 1}^{\infty} (-1)^{n+1} \dfrac{x^n}{\sqrt{n} 2^n}$ .

Apply the Ratio Test to the absolute value series:

$\lim_{n \to \infty} \dfrac{|a_{n+1}|}{|a_n|} = \lim_{n \to \infty} \dfrac{\dfrac{x^{n+1}}{\sqrt{n+1} 2^{n+1}}} {\dfrac{x^n}{\sqrt{n} 2^n}} = \lim_{n \to \infty} \dfrac{2^n}{2^{n+1}} \sqrt{\dfrac{n}{n + 1}} \dfrac{|x|^{n+1}}{|x|^n} = \lim_{n \to \infty} \dfrac{1}{2}\sqrt{\dfrac{n}{n + 1}} |x| = \dfrac{1}{2}|x|.$

The series converges absolutely for $\dfrac{1}{2} |x| < 1$ , i.e. for . It diverges for and for .

I'll check the endpoints separately.

For , the series is

$\sum_{n = 1}^{\infty} (-1)^{n+1} \dfrac{(-2)^n}{\sqrt{n} 2^n} = -\sum_{n = 1}^{\infty} \dfrac{1}{\sqrt{n}}.$

(Since $(-1)^{2 n+1}$ is an odd power of -1, it equals -1 for all n.) The series is (-1 times) a p-series with $p = \dfrac{1}{2}$ , so it diverges.

For , the series is $\displaystyle \sum_{n = 1}^{\infty} (-1)^{n+1} \dfrac{1}{\sqrt{n}}$ . The terms alternate, and

$\lim_{n \to \infty} \dfrac{1}{\sqrt{n}} = 0.$

If $f(n) = \dfrac{1}{\sqrt{n}}$ , then $f'(n) = -\dfrac{1}{2} n^{-3/2} < 0$ for $n \ge 1$ . Therefore, the terms decrease in absolute value. Hence, the series converges, by the Alternating Series Test.

To summarize, the series converges absolutely for , diverges for $x \le 2$ and , and converges conditionally for . The interval of convergence is $-2 < x \le 2$ .

15. Determine the interval of convergence for the power series $\displaystyle \sum_{n = 0}^\infty \dfrac{n^2 (x - 3)^n}{5^n}$ .

Apply the Ratio Test to the absolute value series:

$\lim_{n \to \infty}\dfrac{|a_{n+1}|}{|a_n|} = \lim_{n \to \infty}\dfrac{\dfrac{(n + 1)^2 |x - 3|^{n+1}}{5^{n+1}}} {\dfrac{n^2 |x - 3|^n}{5^n}} = \lim_{n \to \infty}\dfrac{5^n}{5^{n+1}}\cdot \left(\dfrac{n + 1}{n}\right)^2\cdot |x - 3| =$

$\lim_{n \to \infty}\dfrac{1}{5}\cdot \left(\dfrac{n + 1}{n}\right)^2\cdot |x - 3| = \dfrac{1}{5}|x - 3|.$

The series converges absolutely for $\dfrac{1}{5}|x - 3| < 1$ , i.e. for . It diverges for and for .

I'll check the endpoints separately.

At , the series becomes $\displaystyle \sum_{n = 0}^\infty (-1)^n n^2$ . Since $\displaystyle \lim_{n \to \infty} (-1)^n n^2 = \pm \infty$ , the series diverges by the Zero Limit Test.

At , the series becomes $\displaystyle \sum_{n = 0}^\infty n^2$ . Since $\displaystyle \lim_{n \to \infty} n^2 = +\infty$ , the series diverges by the Zero Limit Test.

Thus, the series converges absolutely for , and it diverges for $x \le -2$ and for $x \ge 8$ . The interval of convergence is .

16. Find the Taylor series at for $f(x) = \dfrac{3}{7 - 2 x}$ , and find its interval of convergence.

Since , I want powers of .

$\dfrac{3}{7 - 2 x} = \dfrac{3}{3 - 2(x - 2)} = 3\cdot \dfrac{1}{3 - 2(x - 2)} = \dfrac{1}{1 - \left(\dfrac{2}{3}(x - 2)\right)} =$

$\sum_{n = 0}^\infty \dfrac{2^n}{3^n} (x - 2)^n = 1 + \dfrac{2}{3}(x - 2) + \left(\dfrac{2}{3}(x - 2)\right)^2 + \left(\dfrac{2}{3}(x - 2)\right)^3 + \cdots .$

For the last step, I plugged $u = \dfrac{2}{3}(x - 2)$ into the series

$\dfrac{1}{1 - u} = \sum_{n = 0}^\infty u^n = 1 + u + u^2 + u^3 + \cdots .$

The $\dfrac{1}{1 - u}$ series converges for , so

$\eqalign{ -1 & < u < 1 \cr \noalign{\vskip2 pt} -1 & < \dfrac{2}{3}(x - 2) < 1 \cr \noalign{\vskip2 pt} -\dfrac{3}{2} & < x - 2 < \dfrac{3}{2} \cr \noalign{\vskip2 pt} \dfrac{1}{2} & < x < \dfrac{7}{2} \quad\halmos \cr}$

17. Find the Taylor series at for $f(x) = \dfrac{1}{8 + 3 x}$ , and find its interval of convergence.

Since , I want powers of .

$\dfrac{1}{8 + 3 x} = \dfrac{1}{5 + 3(x + 1)} = \dfrac{1}{5} \dfrac{1}{1 + \dfrac{3}{5} (x + 1)} = \dfrac{1}{5} \dfrac{1}{1 - \left(-\dfrac{3}{5} (x + 1)\right)} =$

$\dfrac{1}{5} \sum_{n = 0}^\infty (-1)^n \dfrac{3^n}{5^n} (x + 1)^n = \dfrac{1}{5} \left(1 - \dfrac{3}{5} (x + 1) + \dfrac{9}{25} (x + 1)^2 - \dfrac{27}{125} (x + 1)^3 + \cdots\right).$

For the last step, I plugged $u = -\dfrac{3}{5} (x + 1)$ into the series

$\dfrac{1}{1 - u} = \sum_{n = 0}^\infty u^n = 1 + u + u^2 + u^3 + \cdots.$

The $\dfrac{1}{1 - u}$ series converges for , so

$\eqalign{ -1 & < u < 1 \cr \noalign{\vskip2 pt} -1 & < -\dfrac{3}{5}(x + 1) < 1 \cr \noalign{\vskip2 pt} -\dfrac{5}{3} & < x + 1 < \dfrac{5}{3} \cr \noalign{\vskip2 pt} -\dfrac{8}{3} & < x < \dfrac{2}{3} \quad\halmos \cr}$

18. Find the Taylor series at for $f(x) = e^{-3 x}$ , and find its interval of convergence.

Use

$e^u = 1 + u + \dfrac{u^2}{2!} + \dfrac{u^3}{3!} + \cdots + \dfrac{u^n}{n!} + \cdots, \quad -\infty < u < \infty.$

Write

$e^{-3 x} = e^{-3(x-1)-3} = e^{-3}e^{-3(x-1)}.$

Setting , I get

$e^{-3 x} = e^{-3} \sum_{n = 0}^\infty \dfrac{(-3)^n (x - 1)^n}{n!} =$

$e^{-3}\left(1 - 3(x - 1) + \dfrac{3^2(x - 1)^2}{2!} - \dfrac{3^3(x - 1)^3}{3!} + \cdots + (-1)^n\dfrac{3^n(x - 1)^n}{n!} + \cdots\right).$

$-\infty < -3(x - 1) < \infty$ gives $-\infty < x < \infty$ . The interval of convergence is $-\infty < x < \infty$ .

19. The angle addition formula for cosine is

$\cos (a + b) = \cos a \cos b - \sin a \sin b.$

Use this formula to find the Taylor series for $\cos x$ expanded at .

$\cos x = \cos [(x - 2) + 2] = [\cos (x - 2)](\cos 2) - [\sin (x - 2)](\sin 2) =$

$(\cos 2) \sum_{n = 0}^\infty (-1)^n \dfrac{(x - 2)^{2 n}}{(2 n)!} - (\sin 2) \sum_{n = 0}^\infty (-1)^n \dfrac{(x - 2)^{2 n + 1}}{(2 n + 1)!}.$

The interval of convergence is $-\infty < x < \infty$ .

20. (a) Find the Taylor series at for $\dfrac{1}{10 - x}$ .

(b) Find the Taylor series at for $f(x) = \dfrac{1}{(10 - x)^2}$ by differentiating the series in (a).

(a) I have

$\dfrac{1}{1 - u} = \sum_{n = 0}^\infty u^n = 1 + u + u^2 + u^3 + u^4 + \cdots.$

Set $u = \dfrac{x}{10}$ :

$\dfrac{1}{10 - x} = \dfrac{1}{10} \dfrac{1}{1 - \dfrac{x}{10}} = \dfrac{1}{10} \sum_{n = 0}^\infty \dfrac{x^n}{10^n} = \dfrac{1}{10} \left(1 + \dfrac{x}{10} + \dfrac{x^2}{100} + \dfrac{x^3}{1000} + \dfrac{x^4}{10000} + \cdots\right).$

(b) Differentiating the series in (a) gives the series for $\dfrac{1}{(10 - x)^2}$ :

$\dfrac{1}{(10 - x)^2} = \der {} x \left(\dfrac{1}{10 - x}\right) = \dfrac{1}{10} \sum_{n = 1}^\infty \dfrac{n x^{n - 1}}{10^n}.$

Here are the first few terms:

$\dfrac{1}{(10 - x)^2} = \dfrac{1}{10} \left(\dfrac{1}{10} + \dfrac{x}{50} + \dfrac{3 x^2}{1000} + \dfrac{x^3}{2500} + \cdots\right).\quad\halmos$

21. (a) Find the Taylor series at for $\dfrac{1}{1 + x^4}$ .

(b) Find the Taylor series at for $f(x) = \dfrac{x^3}{(1 + x^4)^2}$ by differentiating the series in (a).

(a) I'll find the series for $\dfrac{1}{1 + x^4}$ by setting in the series for $\dfrac{1}{1 - u}$ :

$\dfrac{1}{1 + x^4} = \dfrac{1}{1 - (-x^4)} = 1 - x^4 + x^8 - x^{12} + x^{16} - cdots + (-1)^nx^{4 n} + \cdots.$

(b) Note that

$\der {} x \dfrac{1}{1 + x^4} = \dfrac{-4 x^3}{(1 + x^4)^2}, \quad\hbox{so}\quad \dfrac{x^3}{(1 + x^4)^2} = -\dfrac{1}{4} \der {} x \dfrac{1}{1 + x^4}.$

Hence,

$\dfrac{x^3}{(1 + x^4)^2} = -\dfrac{1}{4} \der {} x \dfrac{1}{1 + x^4} = -\dfrac{1}{4} \der {} x \left(1 - x^4 + x^8 - x^{12} + x^{16} - \cdots + (-1)^nx^{4 n} + \cdots\right) =$

$-\dfrac{1}{4}\left(-4 x^3 + 8 x^7 - 12 x^{11} + 16 x^{15} - \cdots + (-1)^n4 nx^{4 n-1} + \cdots\right) =$

$x^3 - 2 x^7 + 3 x^{11} - 4 x^{15} + \cdots + (-1)^{n-1}nx^{4 n-1} + \cdots.\quad\halmos$

22. Suppose that

$f(1) = 5, \quad f'(1) = 2, \quad f''(1) = -2, \quad f^{(3)}(1) = 3.$

Use the $3^{\rm rd}$ degree Taylor polynomial to approximate .

$\eqalign{ p_3(x; 1) & = 5 + 2(x - 1) - \dfrac{2}{2!} (x - 1)^2 + \dfrac{3}{3!} (x - 1)^3 \cr \noalign{\vskip2 pt} p_3(x; 1) & = 5 + 2(x - 1) - (x - 1)^2 + \dfrac{1}{2} (x - 1)^3 \cr}$

$f(1.2) \approx p_3(x; 1) = 5.364.\quad\halmos$

23. Find the Taylor series at for $f(x) = \dfrac{e^x}{e^x + 1}$ up to the term of degree 2.

$f'(x) = \dfrac{(e^x + 1)(e^x) - (e^x)(e^x)}{(e^x + 1)^2} = \dfrac{e^x}{(e^x + 1)^2},$

$f''(x) = \dfrac{(e^x + 1)^2(e^x) - (e^x)(2)(e^x + 1)(e^x)}{(e^x + 1)^4} = \dfrac{(e^x + 1)(e^x) - 2(e^x)(e^x)}{(e^x + 1)^3} = \dfrac{e^x - e^{2 x}}{(e^x + 1)^3}.$

Then

$f(0) = \dfrac{1}{2}, \quad f'(0) = \dfrac{1}{4}, \quad f''(0) = 0.$

$f(x) = \dfrac{1}{2} + \dfrac{1}{4} x + 0 \cdot x^2 + \cdots .\quad\halmos$

Note: "Degree 2" means up to the -term. If the problem had asked for "the first 3 nonzero terms", you would have had to go up to the next term, which turns out to be $-\dfrac{1}{48} x^3$ .

24. The first four terms of the Taylor series at for $f(t) = \sec t \tan t$ are

$\sec t \tan t = t + \dfrac{5}{6} t^3 + \dfrac{61}{120} t^5 + \dfrac{277}{1008} t^7 + \cdots.$

Find the first five terms of the Taylor series for $\sec x$ at .

$\int_0^x \sec t \tan t\,dt = [\sec t]_0^x = \sec x - 1.$

Hence,

$\sec x = 1 + \int_0^x \sec t \tan t\,dt = 1 + \int_0^x \left(t + \dfrac{5}{6} t^3 + \dfrac{61}{120} t^5 + \dfrac{277}{1008} t^7 + \cdots\right)\,dt =$

$1 + \dfrac{1}{2} x^2 + \dfrac{5}{24} x^4 + \dfrac{61}{720} x^6 + \dfrac{277}{8064} x^8 + \cdots.\quad\halmos$

25. If $f(x) = \sin x^3$ , what is $f^{(600)}(0)$ ?

The Taylor series for $\sin x^3$ is

$\sin x^3 = \sum_{n = 0}^{\infty} \dfrac{x^{6 n+3}}{(2 n + 1)!}.$

(Substitute in the series for $\sin u$ .)

The $x^{600}$ term appears when , or $n = \dfrac{597}{6}$ . This is not an integer, so there is no $x^{600}$ term. That is, the coefficient of $x^{600}$ in the Taylor expansion for $\sin x^3$ is 0. On the other hand, the Taylor series formula says that the $x^{600}$ term is $\dfrac{1}{600!} f^{(600)}(0) x^{600}$ . Hence, $\dfrac{1}{600!} f^{(600)}(0) = 0$ , or $f^{(600)}(0) = 0$ .

26. Estimate the error made in using the $3^{\rm rd}$ degree Taylor polynomial to approximate if $0 \le x \le 0.5$ .

$f'(x) = x e^x + e^x, \quad f''(x) = x e^x + 2 e^x, \quad f^{(3)}(x) = x e^x + 3 e^x, \quad f^{(4)}(x) = x e^x + 4 e^x.$

Hence,

$R_4(x; 0) = \dfrac{z e^z + 4 e^z}{4!} x^4.$

Since $0 \le x \le 0.5$ , I have $x^4 \le 0.5^4$ . Also, is an increasing function of z. Since $0 \le z \le x \le 0.5$ , it follows that

$z e^z + 4 e^z \le 0.5 e^{0.5} + 4 e^{0.5} = \dfrac{9}{2} e^{0.5}.$

Thus, the error is approximately

$|R_4(x; 0)| \le \dfrac{\dfrac{9}{2} e^{0.5}}{4!} \cdot 0.5^4 \approx 0.01932.\quad\halmos$

First, I'll compute the first few derivatives of $\cos x$ :

$f'(x) = -\sin x, \quad f''(x) = -\cos x, \quad f'''(x) = \sin x.$

Then

$f'\left(\dfrac{\pi}{3}\right) = -\dfrac{\sqrt{3}}{2}, \quad f''\left(\dfrac{\pi}{3}\right) = -\dfrac{1}{2}.$

The first three terms of the Taylor series for $\cos x$ at $a = \dfrac{\pi}{3}$ are

$\cos x = \dfrac{1}{2} - \dfrac{\sqrt{3}}{2}\left(x - \dfrac{\pi}{3}\right) - \dfrac{1}{4}\left(x - \dfrac{\pi}{3}\right)^2 + \cdots.$

The third term is the term, so . Thus, the remainder term is

$R_2\left(x;\dfrac{\pi}{3}\right) = \dfrac{f'''(z)}{3!} \left(x - \dfrac{\pi}{3}\right)^3.$

$f'''(z) = \sin z$ , and $|\sin z| \le 1$ , so

$|R_2\left(x;\dfrac{\pi}{3}\right)| \le \dfrac{1}{6}\left|x - \dfrac{\pi}{3}\right|^3.$

The error will be less than 0.0001 if the right side is less than 0.0001:

$\dfrac{1}{6} \left|x - \dfrac{\pi}{3}\right|^3 \le 0.0001, \quad \left|x - \dfrac{\pi}{3}\right|^3 \le 0.0006, \quad \left|x - \dfrac{\pi}{3}\right| \le 0.08434.$

That is, the error will be less than 0.0001 within an interval of radius approximately 0.08434 about $\dfrac{\pi}{3}$ .

28. Suppose $0 \le x \le 0.2$ . What is the smallest value of n for which the $n^{\rm th}$ degree Taylor polynomial of $f(x) = e^{-3 x}$ at approximates to an accuracy of at least $10^{-6}$ ?

The Remainder Term is

$R_n(x; 0) = \dfrac{f^{(n+1)}(z)}{(n + 1)!} x^{n+1}.$

I need to find $f^{(n+1)}(z)$ . Compute a few derivatives to find the pattern:

$f'(x) = -3 e^{-3 x}, \quad f''(x) = (-3)^2 e^{-3 x}, \quad f'''(x) = (-3)^3 e^{-3 x}.$

I can see that

$f^{(n+1)}(x) = (-3)^{n+1} e^{-3 x}, \quad\hbox{so}\quad f^{(n+1)}(z) = (-3)^{n+1} e^{-3 z}.$

Therefore,

$R_n(x; 0) = \dfrac{(-3)^{n+1}e^{-3 z}}{(n + 1)!}0.2^{n+1}.$

Since $0 \le x \le 0.2$ , I have $x^{n+1} \le 0.2^{n+1}$ .

Next, $0 \le z \le x \le 0.2$ , so

$0 \ge -3 z \ge -0.6, \quad\hbox{and}\quad e^0 \ge e^{-3 z} \ge e^{-0.6}.$

(Notice that the inequality "flipped" when I multiplied by -3.) Since , I have $e^{-3 z} \le 1$ .

Therefore,

$|R_n(x; 0)| = \dfrac{3^{n+1}e^{-3 z}}{(n + 1)!} x^{n+1} \le \dfrac{3^{n+1}(1)}{(n + 1)!} 0.2^{n+1} = \dfrac{3^{n+1}}{(n + 1)!} 0.2^{n+1} = \dfrac{0.6^{n+1}}{(n + 1)!}.$

I took absolute values because I only care about the size of the error. Doing this changed $(-3)^{n+1}$ to $3^{n+1}$ .

Since $|R_n(x; 0)| \le \dfrac{0.6^{n+1}}{(n + 1)!}$ , if I can make $\dfrac{0.6^{n+1}}{(n + 1)!} < 10^{-6}$ , then putting the two inequalities together gives $|R_n(x; 0)| < 10^{-6}$ , which is what I want.

Thus, I want to find the smallest n for which $\dfrac{0.6^{n+1}}{(n + 1)!} \le 10^{-6}$ . This inequality is too complicated to solve algebraically, so I'll do it by trial-and-error: I plug values of n into the left side until it's less than $10^{-6}$ .

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & n & & $\dfrac{0.6^{n+1}}{(n + 1)!}$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1 & & 0.18000000000000005 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 2 & & 0.03600000000000001 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 3 & & 0.005400000000000001 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 4 & & 0.0006480000000000001 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 5 & & 0.00006480000000000003 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 6 & & $5.554285714285717 \times 10^{-6}$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 7 & & $4.165714285714288 \times 10^{-7}$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }}$

The smallest value of n is . Since the first term is the $0^{\rm th}$ term, this means I need the first 8 terms of the Taylor series (or the $7^{\rm th}$ degree Taylor polynomial) to approximate to within $10^{-6}$ on the interval $0 \le x \le 0.2$ .

29. (a) Find the Taylor series for $\dfrac{\ln (1 + x^2)}{x}$ at .

(b) Express the series using summation notation.

(c) Calvin Butterball is bothered by parts (a) and (b). "How can you define the Taylor series for $f(x) = \dfrac{\ln (1 + x^2)}{x}$ when $\dfrac{\ln (1 + x^2)}{x}$ isn't defined at ?", he whines.

Actually, he has a valid point. Use the series of part (a) to compute

$\lim_{x \to 0} \dfrac{\ln (1 + x^2)}{x}.$

Then use the result to redefine f so that it's at least continuous at .

(d) Find $f^{(91)}(0)$ .

(e) Use the series of part (a) to approximate the following integral to within 0.01:

$\int_0^1 \dfrac{\ln (1 + x^2)}{x}\,dx.$

Justify the accuracy of your approximation using the error estimate for alternating series.

(a) Set in the series for $\ln (1 + u)$ :

$\ln (1 + x^2) = x^2 - \dfrac{x^4}{2} + \dfrac{x^6}{3} - \dfrac{x^8}{4} + \cdots.$

Divide both sides by x:

$\dfrac{\ln (1 + x^2)}{x} = x - \dfrac{x^3}{2} + \dfrac{x^5}{3} - \dfrac{x^7}{4} + \cdots.\quad\halmos$

(b)

$\dfrac{\ln (1 + x^2)}{x} = \sum_{n = 0}^{\infty} (-1)^n \dfrac{x^{2 n+1}}{n + 1}.\quad\halmos$

(c)

$\lim_{x \to 0} \dfrac{\ln (1 + x^2)}{x} = \lim_{x \to 0} \sum_{n = 0}^{\infty} (-1)^n \dfrac{x^{2 n+1}}{n + 1} = 0.$

Hence, define

$f(x) = \cases{ \dfrac{\ln (1 + x^2)}{x} & if $x \ne 0$\cr 0 & if $x = 0$\cr}$

This is the function whose Taylor series I'm finding. Note that all I know is that f is continuous at 0; to construct the Taylor series, I should also show that f is infinitely differentiable at 0. (I'll just take that for granted.)

(d) The term of order 91 in the Taylor series should be $\dfrac{1}{91!} f^{(91)}(0) x^{91}$ .

On the other hand, I know what the series is, and I know that the term of order 91 is $\dfrac{1}{46} x^{91}$ .

Setting the coefficients equal, I get $\dfrac{1}{91!} f^{(91)}(0) = \dfrac{1}{46}$ , or $f^{(91)}(0) = \dfrac{91!}{46}$ .

(e) Integrate the series for $\dfrac{\ln (1 + x^2)}{x}$ term-by-term:

$\int_0^1 \dfrac{\ln (1 + x^2)}{x}\,dx = \int_0^1 \left(x - \dfrac{x^3}{2} + \dfrac{x^5}{3} - \dfrac{x^7}{4} + \cdots \right)\,dx =$

$\left[\dfrac{x^2}{2} - \dfrac{x^4}{4\cdot 2} + \dfrac{x^6}{6\cdot 3} - \dfrac{x^8}{8\cdot 4} + \cdots\right]_0^1 = \dfrac{1}{2} - \dfrac{1}{4\cdot 2} + \dfrac{1}{6\cdot 3} - \dfrac{1}{8\cdot 4} + \cdots.$

By examination, the first term of the series which is less than 0.01 is $\dfrac{1}{16 \cdot 8}$ . Therefore, the sum of the preceding terms approximates the integral to within 0.01, by the error estimate for alternating series. This sum is

$\dfrac{1}{2} - \dfrac{1}{4\cdot 2} + \dfrac{1}{6\cdot 3} - \dfrac{1}{8\cdot 4} + \dfrac{1}{10\cdot 5} - \dfrac{1}{12\cdot 6} + \dfrac{1}{14\cdot 7} \approx 0.42.\quad\halmos$

30. Find parametric equations for the curve .

$x = t, \quad y = t^3 + t + 1.\quad\halmos$

31. Find parametric equations for the curve .

$x = 9 - 8 t - t^2, \quad y = t.\quad\halmos$

32. Find parametric equations for the segment from to . Find a parameter range for which the segment is traced out exactly once.

$\eqalign{ (x, y) & = (1 - t)(8, -5) + t(3, 11) \cr (x, y) & = (8(1 - t), -5(1 - t)) + (3 t, 11 t) \cr (x, y) & = (8 - 8 t, -5 + 5 t) + (3 t, 11 t) \cr (x, y) & = (8 - 8 t + 3 t, -5 + 5 t + 11 t) \cr (x, y) & = (8 - 5 t, -5 + 16 t) \cr}$

The segment is

$x = 8 - 5 t, \quad y = -5 + 16 t, \quad 0 \le t \le 1.\quad\halmos$

33. Find parametric equations for the circle with center and radius 2.

The equation of the circle is

$(x - 5)^2 + (y + 4)^2 = 4, \quad\hbox{or}\quad \dfrac{(x - 5)^2}{4} + \dfrac{(y + 4)^2}{4} = 1.$

Match this up against the identity $(\cos t)^2 + (\sin t)^2 = 1$ .

$\eqalign{ \dfrac{(x - 5)^2}{4} & = (\cos t)^2 \cr \noalign{\vskip2 pt} (x - 5)^2 & = 4 (\cos t)^2 \cr x - 5 & = 2 \cos t \cr x & = 5 + 2 \cos t \cr}$

$\eqalign{ \dfrac{(y + 4)^2}{4} & = (\sin t)^2 \cr \noalign{\vskip2 pt} (y + 4)^2 & = 4 (\sin t)^2 \cr y + 4 & = 2 \sin t \cr y & = -4 + 2 \sin t \cr}$

The parametric equations are

$x = 5 + 2 \cos t, \quad y = -4 + 2 \sin t, \quad 0 \le t \le 2 \pi.$

Notes: (a) The range $0 \le t \le 2 \pi$ traces out the circle once counterclockwise, except that and $t = 2 \pi$ give the same point.

(b) If you match the x-term against $(\sin t)^2$ and the y-term against $(\cos t)^2$ and follow the procedure above, you'll get a valid parametrization. However, the circle will be traced out clockwise as t goes from 0 to $2 \pi$ . Since counterclockwise is the direction of increasing angle, it is usually chosen by convention to be the "positive" direction. This may be an issue if you ever use this kind of parametrization to do line integrals. For that reason, I think the approach above is better.

34. Find an x-y equation for the curve whose parametric equations are

$x = t + 2, \quad y = t^2 + 5.$

Solve the x-equation for t to get .

Plug into the y-equation to get

$y = (x - 2)^2 + 5 = x^2 - 4 x + 9.\quad\halmos$

35. Find an x-y equation for the curve whose parametric equations are

$x = 2 \cos t + 6, \quad y = 3 \sin t + 5.$

Solve the x-equation for $\cos t$ :

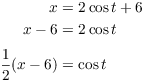
$\eqalign{ x & = 2 \cos t + 6 \cr x - 6 & = 2 \cos t \cr \noalign{\vskip2 pt} \dfrac{1}{2} (x - 6) & = \cos t \cr}$

Solve the y-equation for $\sin t$ :

$\eqalign{ y & = 3 \sin t + 5 \cr y - 5 & = 3 \sin t \cr \noalign{\vskip2 pt} \dfrac{1}{3} (y - 5) & = \sin t \cr}$

Plug $\cos t = \dfrac{1}{2} (x - 6)$ and $\sin t = -\dfrac{1}{3} (y - 5)$ into the identity $(\cos t)^2 + (\sin t)^2 = 1$ :

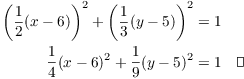
$\eqalign{ \left(\dfrac{1}{2} (x - 6)\right)^2 + \left(\dfrac{1}{3} (y - 5)\right)^2 & = 1 \cr \dfrac{1}{4} (x - 6)^2 + \dfrac{1}{9} (y - 5)^2 & = 1 \quad\halmos \cr}$

36. and $y = e^{2 t} + 1$ is a parametrization of part of the curve , but it does not represent the whole curve. Why not?

Since for all t, the parametrization can only represent the part of the parabola to the right of the y-axis.

If you want a parametrization that could give the whole parabola, you could use (for instance) and .

37. Find the value(s) of t for which the following curve has horizontal tangents, and the value(s) for which it has vertical tangents:

$x = (t + 1)^2, \quad y = t^3 - 6 t^2 - 36 t + 5.$

$\der y x = \dfrac{\der y t}{\der x t} = \dfrac{3 t^2 - 12 t - 36}{2(t + 1)} = \dfrac{3(t - 6)(t + 2)}{2(t + 1)}.$

The curve has horizontal tangents when $\der y x = 0$ . This occurs if or .

The curve has vertical tangents when $\der y x$ is undefined. This occurs if .

38. Find the points at which the following parametric curves intersect:

$\left\{\matrix{x = s \cr y = s^2 + s + 1 \cr}\right. \quad\hbox{and}\quad \left\{\matrix{x = t + 1 \cr y = 2 t + 5 \cr}\right.$

Equating the two x-expressions gives

Plug into :

But , so

$\eqalign{ t^2 + 3 t + 3 & = 2 t + 5 \cr t^2 + t - 2 & = 0 \cr (t + 2)(t - 1) & = 0 \cr}$

This gives and .

Plugging into and gives the point .

The curves intersect at and at .

39. Consider the parametric curve

$x = t^2 + t + 1, \quad y = t^3 - 5 t + 2.$

(a) Find the equation of the tangent line at .

(b) Find $\dfrac{d^2 y}{dx^2}$ at .

(a)

$\der y x= \dfrac{\der y t}{\der x t} = \dfrac{3 t^2 - 5}{2 t + 1}.$

When , I have and , and $\der y x = -\dfrac{2}{3}$ . The equation of the tangent line is

$y + 2 = -\dfrac{2}{3}(x - 3).\quad\halmos$

(b)

$\dfrac{d^2 y}{dx^2} = \dfrac{\der {} t \left(\der y x\right)}{\der x t} = \dfrac{\der {} t \left(\dfrac{3 t^2 - 5}{2 t + 1}\right)}{2 t + 1} = \dfrac{\dfrac{(2 t + 1)(6 t) - (3 t^2 - 5)(2)}{(2 t + 1)^2}} {2 t + 1} = \dfrac{6 t^2 + 6 t + 10}{(2 t + 1)^3}.$

When , $\dfrac{d^2 y}{dx^2} = \dfrac{22}{27}$ .

40. Find $\dfrac{d^2 y}{dx^2}$ at for the parametric curve

$x = t^2 + 2 t + 2, \quad y = t^3 + 1.$

$\der y x = \dfrac{3 t^2}{2 t + 2}.$

Then

$\dfrac{d^2 y}{dx^2} = \dfrac{\der {} t \der y x}{\der x t} = \dfrac{\der {} t \dfrac{3 t^2}{2 t + 2}}{2 t + 2} = \dfrac{\dfrac{(2 t + 2)(6 t) - (3 t^2)(2)}{(2 t + 2)^2}}{2 t + 2} = \dfrac{(2 t + 2)(6 t) - (3 t^2)(2)}{(2 t + 2)^3}.$

When ,

$\dfrac{d^2 y}{dx^2} = \dfrac{(6)(12) - (12)(2)}{6^3} = \dfrac{2}{9}.\quad\halmos$

It breeds great perfection, if the practice be harder than the use. - Francis Bacon

Contact information

Bruce Ikenaga's Home Page