Review Sheet for Test 1

Math 311

These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the absence of a topic does not imply that it won't appear on the test.

1. Compute:

(a) $(2, -1, 3) + 5 \cdot (4, 1, 2)$ .

(b) $\|(7, -2, 1)\|$ .

2. Compute:

(a) $\displaystyle -3 \cdot \left[\matrix{-3 & 1 \cr 5 & 5 \cr 5 & -6 \cr}\right] + \left[\matrix{1 & 2 \cr 2 & 0 \cr 3 & -1 \cr}\right]$

(b) $\displaystyle \left[\matrix{2 & 0 \cr 4 & 1 \cr}\right] \left[\matrix{2 & -2 & 3 \cr -2 & -3 & 5 \cr}\right]$

(c) $\displaystyle \left[\matrix{-1 & 4 \cr -2 & 1 \cr 4 & -1 \cr}\right] \left[\matrix{5 & 5 & 2 & -2 \cr 3 & 5 & 4 & -1 \cr}\right]$

3. Find the inverse of $\displaystyle \left[\matrix{4 & 5 \cr -3 & 2 \cr}\right]$ .

4. Compute the determinant: $\displaystyle \det \left[\matrix{2 & 1 & 8 \cr 0 & 4 & 3 \cr 1 & 1 & 2 \cr}\right]$ .

5. Suppose that

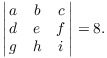
$$\left|\matrix{ a & b & c \cr d & e & f \cr g & h & i \cr}\right| = 8.$$

Find:

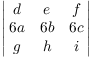(a) $\displaystyle \left|\matrix{d & e & f \cr 6 a & 6 b & 6 c \cr g & h & i \cr}\right|$ .

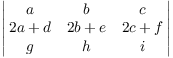(b) $\displaystyle \left|\matrix{a & b & c \cr 2 a + d & 2 b + e & 2 c + f \cr g & h & i \cr}\right|$ .

6. (a) Find the vector from $P(2, 3, 0)$ to $Q(5, 5, -4)$ .

(b) Find two unit vectors perpendicular to the vector $(-12, 5)$ .

(c) Find the vector of length 7 that has the same direction as $(1, 2, -2)$ .

(d) Find a vector which points in the opposite direction to $(1, -1, 3)$ and has 7 times the length.

(e) Find the scalar component of $\vec v = (1, 2, -4)$ in the direction of $\vec w = (2, 1, 3)$ .

(f) Find the vector projection of $\vec v = (1, 1, -4)$ in the direction of $\vec w = (2, 0, 5)$ .

(g) Find the angle in radians between the vectors $\vec{v} = (1, 1, -2)$ and $\vec{w} = (5, -3, 0)$ .

7. (a) Find the area of the parallelogram $ABCD$ for the points $A(1, 1, 2)$ , $B(4, 0, 2)$ , $C(3, 0, 3)$ , and $D(0, 1, 3)$ .

(b) Find the area of the triangle with vertices $A(2, 5, 4)$ , $B(-1, 3, 4)$ , and $C(1, 1, -1)$ .

(c) Find the volume of the rectangular parallelepiped determined by the vectors $(1, 2, -4)$ , $(1, 1, 1)$ , and $( 0, 3, 1)$ .

8. Find the distance from the point $P(1, 0, -3)$ to the line

$$x = 1 + 2 t, \quad y = -t, \quad z = 2 + 2 t.$$

9. (a) Find the equation of the line which passes through the points $(2, -1, 3)$ and $(4, 2, 1)$ .

(b) Where does the line in part (a) intersect the y-z plane?

10. (a) Find the equation of the line which goes through the point $(5, 1, 4)$ and is parallel to the vector $(1, 2, -2 )$ .

(b) Find the point on the line in part (a) which is closest to the origin.

11. Find the line which passes through the point $(2, -3, 1)$ and is parallel to the line containing the points $(3, 9, 5)$ and $(4, 7, 2)$ .

12. Determine whether the following lines are parallel, skew, or intersect. If they intersect, find the point of intersection.

(a)

$$x = 1 + 2 t, \quad y = 1 - 4 t, \quad z = 5 - t,$$

$$x = 4 - v, \quad y = -1 + 6 v, \quad z = 4 + v.$$

(b)

$$x = 3 + t, \quad y = 2 - 4 t, \quad z = t,$$

$$x = 4 - s, \quad y = 3 + s, \quad z = -2 + 3 s.$$

(c)

$$x = 1 + 2 t, \quad y = -6 t, \quad z = 11 + 4 t,$$

$$x = 7 - 5 s, \quad y = 2 + 15 s, \quad z = -10 s.$$

13. Find the equation of the plane:

(a) Which is perpendicular to the vector $(2, 1, 3)$ and passes through the point $(1, 1, 7)$ .

(b) Which contains the point $(4, -5, -1)$ and is perpendicular to the line

$$x = 3 - t, \quad y = 4 + 4 t, \quad z = 9.$$

(c) Which contains the parallel lines

$$x = s, \quad y = 3 + 2 s, \quad z = 1 - 2 s,$$

$$x = 3 t, \quad y = 1 + 6 t, \quad z = 5 - 6 t.$$

14. Find the point on the plane $2 x + y + 3 z = 6$ closest to the origin.

15. Find the equation of the plane which goes through the point $(1, 3, -1)$ and is parallel to the plane $3 x - 2 y + 6 z = 9$ .

16. Find the equation of the line of intersection of the planes

$$2 x - 3 y + z = 0 \quad\hbox{and}\quad x + y + z = 4.$$

17. Find the distance from the point $(-6, 2, 3)$ to the plane $4 x - 5 y + 8 z = 7$ .

18. (a) Show that the following lines intersect:

$$x = 2 + 3 t, \quad y = -4 - 2 t, \quad z = -1 + 4 t,$$

$$x = 6 + 4 s, \quad y = -2 + 2 s, \quad z = -3 - 2 s.$$

(b) Find the equation of the plane containing the two lines in part (a).

19. Find the distance between the skew lines

$$x = 3 + t, \quad y = 2 - 4 t, \quad z = t,$$

$$x = 4 - s, \quad y = 3 + s, \quad z = -2 + 3 s.$$

20. (a) Parametrize the segment from $P(2, -3, 5)$ to $Q(-10, 0, 6)$ .

(b) Parametrize the curve of intersection of the paraboloid $z = x^2 + y^2$ and the plane $2 x - 4 y + z = 4$ .

(c) Parametrize the curve of intersection of the cylinder $x^2 + 4 y^2 = 25$ with the plane $x - 3 y + z = 7$ .

21. (a) Parametrize the surface $x^2 + y^2 + 4 z^2 = 9$ .

(b) Parametrize the surface $x^2 + y^2 = 7$ .

(c) Parametrize the surface generated by revolving the curve $y = \sin x$ about the x-axis.

(d) Parametrize the surface $y = x^3 + 3 x z - z^2$ .

(e) Parametrize the parallelogram having $P(5, -4, 7)$ as a vertex, where $\vec{v} = (3, 3, 0)$ and $\vec{w} = (8, -1, 3)$ are the sides of the parallelogram which emanate from P.

(f) Parametrize the part of the surface $y = x^2$ lying between the x-y-plane and $z = x + 2 y + 3$ .

22. Let

$$g(t) = (7 t^2 + 13 t + 4, 110, 6 t - e^{2 t}).$$

Compute $g'(t)$ and $g'(1)$ .

23. The position of a cheesesteak stromboli at time t is

$$\vec{f}(t) = (e^{t^2}, \ln (t^2 + 1), \tan t).$$

(a) Find the velocity and acceleration of the stromboli at $t = 1$ .

(b) Find the speed of the stromboli at $t = 1$ .

24. The acceleration of a cheeseburger at time t is

$$\vec{a}(t) = (6 t, 4, 4 e^{2 t}).$$

Find the position $\vec{f}(t)$ if $\vec{v}(1) = (5, 6, 2 e^2 - 3)$ and $\vec{f}(0) = (1, 3, 2)$ .

25. Compute $\displaystyle \int \left(t^2\cos 2 t, t^2 e^{t^3}, \dfrac{1}{\sqrt{t}}\right)\,dt$ .

26. Find the length of the curve

$$x = \dfrac{1}{2}t^2 + 1, \quad y = \dfrac{8}{3}t^{3/2} + 1, \quad z = 8 t - 2, \quad 0 \le t \le 1.$$

27. Find the unit tangent vector to:

(a) $\vec{f}(t) = \left(t^2 + t + 1, \dfrac{1}{t}, \sqrt{6} t\right)$ at $t = 1$ .

(b) $\vec{f}(t) = (\cos 5 t, \sin 5 t, 3 t)$ .

28. Find the curvature of:

(a) $y = \tan x$ at $x = \dfrac{\pi}{4}$ .

(b) $\vec{f}(t) = (t^2 + 1, 5 t + 1, 1 - t^3)$ at $t = 1$ .

29. Find the unit tangent and unit normal for the curve $y = \dfrac{1}{3}x^3 + x^2 + 3 x + \dfrac{2}{3}$ at the point $(1, 5)$ .

30. Find the unit tangent, the unit normal, the binormal, and the osculating circle at $t = 1$ for the curve

$$\vec{f}(t) = \left(\dfrac{1}{3}t^3 + 1, t^2 + 1, 2 t + 5\right).$$

Solutions to the Review Sheet for Test 1

1. Compute:

(a) $(2, -1, 3) + 5 \cdot (4, 1, 2)$ .

(b) $\|(7, -2, 1)\|$ .

(a)

$$(2, -1, 3) + 5 \cdot (4, 1, 2) = (2, -1, 3) + (20, 5, 10) = (22, 4, 13).\quad\halmos$$

(b)

$$\|(7, -2, 1)\| = \sqrt{49 + 4 + 1} = \sqrt{54}.\quad\halmos$$

2. Compute:

(a) $\displaystyle -3 \cdot \left[\matrix{-3 & 1 \cr 5 & 5 \cr 5 & -6 \cr}\right] + \left[\matrix{1 & 2 \cr 2 & 0 \cr 3 & -1 \cr}\right]$

(b) $\displaystyle \left[\matrix{2 & 0 \cr 4 & 1 \cr}\right] \left[\matrix{2 & -2 & 3 \cr -2 & -3 & 5 \cr}\right]$

(c) $\displaystyle \left[\matrix{-1 & 4 \cr -2 & 1 \cr 4 & -1 \cr}\right] \left[\matrix{5 & 5 & 2 & -2 \cr 3 & 5 & 4 & -1 \cr}\right]$

(a)

$$-3 \cdot \left[\matrix{ -3 & 1 \cr 5 & 5 \cr 5 & -6 \cr}\right] + \left[\matrix{ 1 & 2 \cr 2 & 0 \cr 3 & -1 \cr}\right] = \left[\matrix{ 10 & -1 \cr -13 & -15 \cr -12 & 17 \cr}\right].\quad\halmos$$

(b)

$$\left[\matrix{ 2 & 0 \cr 4 & 1 \cr}\right] \left[\matrix{ 2 & -2 & 3 \cr -2 & -3 & 5 \cr}\right] = \left[\matrix{ 4 & -4 & 6 \cr 6 & -11 & 17 \cr}\right].\quad\halmos$$

(c)

$$\left[\matrix{ -1 & 4 \cr -2 & 1 \cr 4 & -1 \cr}\right] \left[\matrix{ 5 & 5 & 2 & -2 \cr 3 & 5 & 4 & -1 \cr}\right] = \left[\matrix{ 7 & 15 & 14 & -2 \cr -7 & -5 & 0 & 3 \cr 17 & 15 & 4 & -7 \cr}\right].\quad\halmos$$

3. Find the inverse of $\displaystyle \left[\matrix{4 & 5 \cr -3 & 2 \cr}\right]$ .

$$\left[\matrix{4 & 5 \cr -3 & 2 \cr}\right]^{-1} = \dfrac{1}{(4)(2) - (5)(-3)} \left[\matrix{2 & -5 \cr 3 & 4 \cr}\right] = \dfrac{1}{23} \left[\matrix{2 & -5 \cr 3 & 4 \cr}\right].\quad\halmos$$

4. Compute the determinant: $\displaystyle \det \left[\matrix{2 & 1 & 8 \cr 0 & 4 & 3 \cr 1 & 1 & 2 \cr}\right]$ .

I'll use cofactors of the first column, since it contains a 0:

$$\det \left[\matrix{2 & 1 & 8 \cr 0 & 4 & 3 \cr 1 & 1 & 2 \cr}\right] = 2 \cdot \det \left[\matrix{4 & 3 \cr 1 & 2 \cr}\right] - 0 \cdot \det \left[\matrix{1 & 8 \cr 1 & 2 \cr}\right] + 1 \cdot \det \left[\matrix{1 & 8 \cr 4 & 3 \cr}\right] =$$

$$2 \cdot 5 - 0 \cdot (-6) + 1 \cdot (-29) = -19.\quad\halmos$$

5. Suppose that

$$\left|\matrix{ a & b & c \cr d & e & f \cr g & h & i \cr}\right| = 8.$$

Find:

(a) $\displaystyle \left|\matrix{d & e & f \cr 6 a & 6 b & 6 c \cr g & h & i \cr}\right|$ .

(b) $\displaystyle \left|\matrix{a & b & c \cr 2 a + d & 2 b + e & 2 c + f \cr g & h & i \cr}\right|$ .

(a)

$$\left|\matrix{ d & e & f \cr 6 a & 6 b & 6 c \cr g & h & i \cr}\right| = 6 \cdot \left|\matrix{ d & e & f \cr a & b & c \cr g & h & i \cr}\right| = -6 \cdot \left|\matrix{ a & b & c \cr d & e & f \cr g & h & i \cr}\right| = (-6) \cdot 8 = -48.\quad\halmos$$

(b)

$$\left|\matrix{ a & b & c \cr 2 a + d & 2 b + e & 2 c + f \cr g & h & i \cr}\right| = \left|\matrix{ a & b & c \cr 2 a & 2 b & 2 c \cr g & h & i \cr}\right| + \left|\matrix{ a & b & c \cr d & e & f \cr g & h & i \cr}\right| =$$

$$2 \cdot \left|\matrix{ a & b & c \cr a & b & c \cr g & h & i \cr}\right| + \left|\matrix{ a & b & c \cr d & e & f \cr g & h & i \cr}\right| = 2 \cdot 0 + 8 = 8.\quad\halmos$$

6. (a) Find the vector from $P(2, 3, 0)$ to $Q(5, 5, -4)$ .

(b) Find two unit vectors perpendicular to the vector $(-12, 5)$ .

(c) Find the vector of length 7 that has the same direction as $(1, 2, -2)$ .

(d) Find a vector which points in the opposite direction to $(1, -1, 3)$ and has 7 times the length.

(e) Find the scalar component of $\vec v = (1, 2, -4)$ in the direction of $\vec w = (2, 1, 3)$ .

(f) Find the vector projection of $\vec v = (1, 1, -4)$ in the direction of $\vec w = (2, 0, 5)$ .

(g) Find the angle in radians between the vectors $\vec{v} = (1, 1, -2)$ and $\vec{w} = (5, -3, 0)$ .

(a)

$$\bvec{P Q} = (3, 2, -4).\quad\halmos$$

(b) $(a, b)$ is perpendicular to $(-12, 5)$ if and only if their dot product is 0:

$$(-12, 5)\cdot (a, b) = 0, \quad -12 a + 5 b = 0.$$

There are infinitely many pairs of numbers $(a, b)$ which satisfy this equation. For example, $a = 5$ and $b = 12$ works. Thus, $(5, 12)$ is perpendicular to $(-12, 5)$ .

I can get a unit vector by dividing $(5, 12)$ by its length:

$$\dfrac{(5, 12)}{\|(5, 12)\|} = \dfrac{1}{13} (5, 12).$$

I can get a second unit vector by taking the negative of the first: $-\dfrac{1}{13} (5, 12)$ .

Thus, $\pm \dfrac{1}{13} (5, 12)$ are two unit vectors perpendicular to $(-12, 5)$ .

(c)

$$\|(1, 2, -2)\| = \sqrt{1^2 + 2^2 + (-2)^2} = 3.$$

Hence, the vector $\dfrac{1}{3} (1, 2, -2)$ is a unit vector --- i.e. a vector with length 1 having the same direction as $(1, 2, -2)$ .

Multiplying this vector by 7, I find that $\dfrac{7}{3} (1, 2, -2)$ is a vector of length 7 that has the same direction as $(1, 2, -2)$ .

(d) Multiplying by -1 gives a vector pointing in the opposite direction; multiplying by 7 gives a vector with 7 times the length. Hence, multiplying by -7 gives a vector which points in the opposite direction and has 7 times the length.

The vector I want is $-7(1, -1, 3) = (-7, 7, -21)$ .

(e)

$$\comp_{\vec w} \vec v = \dfrac{\vec v\cdot \vec w}{\|\vec w\|} = \dfrac{(1, 2, -4)\cdot (2, 1, 3)} {\|(2, 1, 3)\|} = \dfrac{2 + 2 - 12}{\sqrt{4 + 1 + 9}} = -\dfrac{8}{\sqrt{14}}.\quad\halmos$$

(f)

$$\proj_{\vec w} \vec v = \dfrac{\vec v\cdot \vec w}{\|\vec w\|^2}\vec w = \dfrac{(1, 1, -4)\cdot (2, 0, 5)} {\|(2, 0, 5)\|^2} (2, 0, 5) = \dfrac{2 + 0 - 20}{4 + 0 + 25} (2, 0, 5) = -\dfrac{18}{29} (2, 0, 5).\quad\halmos$$

(g)

$$\cos \theta = \dfrac{\vec{v}\cdot \vec{w}}{\|\vec{v}\|\|\vec{w}\|} = \dfrac{(1, 1, -2)\cdot (5, -3, 0)} {\|(1, 1, -2)\|\|(5, -3, 0)\|} = \dfrac{5 - 3 + 0}{\sqrt{6}\sqrt{34}} = \dfrac{2}{\sqrt{204}}, \quad\hbox{so}\quad \theta = \cos^{-1} \dfrac{2}{\sqrt{204}} \approx 1.43031.\quad\halmos$$

7. (a) Find the area of the parallelogram $ABCD$ for the points $A(1, 1, 2)$ , $B(4, 0, 2)$ , $C(3, 0, 3)$ , and $D(0, 1, 3)$ .

(b) Find the area of the triangle with vertices $A(2, 5, 4)$ , $B(-1, 3, 4)$ , and $C(1, 1, -1)$ .

(c) Find the volume of the rectangular parallelepiped determined by the vectors $(1, 2, -4)$ , $(1, 1, 1)$ , and $( 0, 3, 1)$ .

(a) Since A, B, C, and D (in that order) are the vertices going around the parallelogram, the vertices adjacent to A are B and D. I have

$$\bvec{A B} = (3, -1, 0) \quad\hbox{and}\quad \bvec{A D} = (-1, 0, 1).$$

The cross product is

$$\bvec{A B} \times\bvec{A D} = \left|\matrix{ \ihat & \jhat & \khat \cr 3 & -1 & 0 \cr -1 & 0 & 1 \cr}\right| = (-1, -3, -1).$$

The area of the parallelogram is the length of the cross product:

$$\|(-1, -3, -1)\| = \sqrt{11}.\quad\halmos$$

(b) I have

$$\bvec{A B} = (-3, -2, 0) \quad\hbox{and}\quad \bvec{A C} = (-1, -4, -5).$$

The cross product is

$$\bvec{A B} \times\bvec{A C} = \left|\matrix{\ihat & \jhat & \khat \cr -3 & -2 & 0 \cr -1 & -4 & -5 \cr}\right| = (10, -15, 10).$$

Since a triangle is half of a parallelogram, the area of the triangle is half the length of the cross product:

$$\dfrac{1}{2}\|(10, -15, 10)\| = \dfrac{1}{2}\sqrt{425} = \dfrac{5}{2}\sqrt{17}.\quad\halmos$$

(c) Use the vectors as the rows of a $3 \times 3$ matrix and take the determinant:

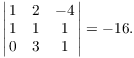
$$\left|\matrix{1 & 2 & -4 \cr 1 & 1 & 1 \cr 0 & 3 & 1 \cr}\right| = -16.$$

Therefore, the volume is 16.

8. Find the distance from the point $P(1, 0, -3)$ to the line

$$x = 1 + 2 t, \quad y = -t, \quad z = 2 + 2 t.$$

Setting $t = 0$ gives $x = 1$ , $y = 0$ , and $z = 2$ , so the point $Q(1, 0, 2)$ is on the line. Therefore, $\vec {PQ} = (0, 0, 5)$ .

The vector $\vec v = (2, -1, 2 )$ is parallel to the line.

Therefore,

$$\comp_{\vec v} \bvec{PQ} = \dfrac{(0, 0, 5) \cdot (2, -1, 2)} {\|(2, -1, 2 )\|} = \dfrac{10}{3}.$$

The distance from P to the line is the leg of a right triangle, and I've found the hypotenuse ($|\vec {PQ}|$ ) and the other leg ($\comp_{\vec v} \bvec {PQ}$ ).

$$\hbox{\epsfysize=1.75 in \epsffile{rev1-1.eps}}$$

By Pythagoras' theorem,

$$\hbox{distance} = \sqrt{|\vec {PQ}|^2 - \left(\comp_{\vec v} \bvec {PQ}\right)^2} = \sqrt{25 - \dfrac{100}{9}} = \dfrac{5\sqrt{5}}{3} \approx 3.72678.\quad\halmos$$

9. (a) Find the equation of the line which passes through the points $(2, -1, 3)$ and $(4, 2, 1)$ .

(b) Where does the line in part (a) intersect the y-z plane?

(a) The vector from the first point to the second is $(2, 3, -2)$ , and this vector is parallel to the line. $(2, -1, 3)$ is a point on the line. Therefore, the line is

$$x - 2 = 2 t, \quad y + 1 = 3 t, \quad z - 3 = -2 t.\quad\halmos$$

(b) The x-z plane is $x = 0$ . Setting $x = 0$ in $x - 2 = 2 t$ gives $-2 = 2 t$ , or $t = -1$ . Plugging this into the y and z equations yields $y = -4$ and $z = 5$ . Therefore, the line intersects the y-z plane at $(0, -4, 5)$ .

10. (a) Find the equation of the line which goes through the point $(5, 1, 4)$ and is parallel to the vector $(1, 2, -2 )$ .

(b) Find the point on the line in part (a) which is closest to the origin.

(a)

$$x - 5 = t, \quad y - 1 = 2 t, \quad z - 4 = -2 t.\quad\halmos$$

(b) The distance from the origin $(0, 0, 0)$ to the point $(x, y, z)$ is

$$\sqrt{(x - 0)^2 + (y - 0)^2 + (z - 0)^2} = \sqrt{x^2 + y^2 + z^2}.$$

Since the distance is smallest when its square is smallest, I'll minimize the square of the distance, which is

$$S = x^2 + y^2 + z^2.$$

(This makes the derivatives easier, since there is no square root.) Since $(x, y, z)$ is on the line, I can substitute $x - 5 = t$ , $y - 1 = 2 t$ , and $z - 4 = -2 t$ to obtain

$$S = (5 + t)^2 + (1 + 2 t)^2 + (4 - 2 t)^2.$$

Hence,

$$\der S t = 2(5 + t) + 4(1 + 2 t) - 4(4 - 2 t) = -2 + 18 t \quad\hbox{and}\quad \dfrac{d^2 S}{dt^2} = 18.$$

Set $\der S t = 0$ . I get $-2 + 18 t = 0$ , or $t = \dfrac{1}{9}$ . $\dfrac{d^2 S}{dt^2} = 18 > 0$ , so the critical point is a local min; since it's the only critical point, it's an absolute min.

Plugging $t = \dfrac{1}{9}$ into the x-y-z equations gives $x = \dfrac{46}{9}$ , $y = \dfrac{11}{9}$ , and $z = \dfrac{34}{9}$ . Thus, the closest point is $\left(\dfrac{46}{9},\dfrac{11}{9},\dfrac{34}{9}\right)$ .

11. Find the line which passes through the point $(2, -3, 1)$ and is parallel to the line containing the points $(3, 9, 5)$ and $(4, 7, 2)$ .

The vector from $(3, 9, 5)$ to $(4, 7, 2)$ is $(1, -2, -3)$ ; it is parallel to the line containing $(3, 9, 5)$ and $(4, 7, 2)$ . The line I want to construct is parallel to this line, so it is also parallel to the vector $(1, -2, -3)$ .

Since the point $(2, -3, 1)$ is on the line I want to construct, the line is

$$x - 2 = t, \quad y + 3 = -2 t, \quad z - 1 = -3 t.\quad\halmos$$

12. Determine whether the following lines are parallel, skew, or intersect. If they intersect, find the point of intersection.

(a)

$$x = 1 + 2 t, \quad y = 1 - 4 t, \quad z = 5 - t,$$

$$x = 4 - v, \quad y = -1 + 6 v, \quad z = 4 + v.$$

(b)

$$x = 3 + t, \quad y = 2 - 4 t, \quad z = t,$$

$$x = 4 - s, \quad y = 3 + s, \quad z = -2 + 3 s.$$

(c)

$$x = 1 + 2 t, \quad y = -6 t, \quad z = 11 + 4 t,$$

$$x = 7 - 5 s, \quad y = 2 + 15 s, \quad z = -10 s.$$

(a) The vector $(2, -4, -1)$ is parallel to the first line. The vector $(-1, 6, 1)$ is parallel to the second line. The vectors aren't multiples of one another, so the vectors aren't parallel. Therefore, the lines aren't parallel.

Next, I'll check whether the lines intersect.

Solve the x-equations simultaneously:

$$1 + 2 t = 4 - v, \quad v = 3 - 2 t.$$

Set the y-expressions equal, then plug in $v = 3 - 2 t$ and solve for t:

$$1 - 4 t = -1 + 6 v, \quad 1 - 4 t = -1 + 6(3 - 2 t), \quad 1 - 4 t = 17 - 12 t, \quad t = 2.$$

Therefore, $v = 3 - 2 t = -1$ .

Check the values for consistency by plugging them into the z-equations:

$$z = 5 - t = 5 - 2 = 3, \quad z = 4 + v = 4 + (-1) = 3.$$

The equations are consistent, so the lines intersect. If I plug $t = 2$ into the x-y-z equations, I obtain $x = 5$ , $y = -7$ , and $z = 3$ . The lines intersect at $(5, -7, 3)$ .

(b) The vector $(1, -4, 1)$ is parallel to the first line. The vector $(-1, 1, 3)$ is parallel to the second line. The vectors aren't multiples of one another, so the vectors aren't parallel. Therefore, the lines aren't parallel.

Next, I'll check whether the lines intersect.

Solve the x-equations simultaneously:

$$3 + t = 4 - s, \quad t = 1 - s.$$

Set the y-expressions equal, then plug in $t = 1 - s$ and solve for s:

$$2 - 4 t = 3 + s, \quad 2 - 4(1 - s) = 3 + s, \quad -2 + 4 s = 3 + s, \quad s = \dfrac{5}{3}.$$

Therefore, $t = 1 - s = -\dfrac{2}{3}$ .

Check the values for consistency by plugging them into the z-equations:

$$z = t = -\dfrac{2}{3}, \quad z = -2 + 3 s = 3.$$

The equations are inconsistent, so the lines do not intersect.

Since the lines aren't parallel and don't intersect, they must be skew.

(c) The vector $(2, -6, 4)$ is parallel to the first line. The vector $(-5, 15, -10)$ is parallel to the second line. Note that

$$-\dfrac{5}{2} \cdot (2, -6, 4) = (-5, 15, -10).$$

Since the vectors are multiples, they are parallel. Therefore, the lines are parallel.

It is possible for parallel lines to intersect, if they are the same line. I can tell whether this is the case by taking a point on one line and seeing if it is on the other. Set $t = 0$ in the first line; I get the point $P(1, 0, 11)$ .

If I set $x = 1$ in $x = 7 - 5 s$ , I get

$$7 - 5 s = 1, \quad\hbox{so}\quad s = \dfrac{5}{6}.$$

But if I set $y = 0$ in $y = 2 + 15 s$ , I get

$$2 + 15 s = 0, \quad\hbox{so}\quad s = -\dfrac{2}{15}.$$

Sine the values of s don't agree, $P(1, 0, 11)$ is on the first line, but not on the second. Hence, the lines are parallel, and not the same.

13. Find the equation of the plane:

(a) Which is perpendicular to the vector $(2, 1, 3)$ and passes through the point $(1, 1, 7)$ .

(b) Which contains the point $(4, -5, -1)$ and is perpendicular to the line

$$x = 3 - t, \quad y = 4 + 4 t, \quad z = 9.$$

(c) Which contains the parallel lines

$$x = s, \quad y = 3 + 2 s, \quad z = 1 - 2 s,$$

$$x = 3 t, \quad y = 1 + 6 t, \quad z = 5 - 6 t.$$

(a)

$$2(x - 1) + (y - 1) + 3(z - 7) = 0, \quad\hbox{or}\quad 2 x + y + 3 z = 24.\quad\halmos$$

(b) The vector $(-1, 4, 0)$ is parallel to the line. The line is perpendicular to the plane. Hence, the vector $(-1, 4, 0)$ is perpendicular to the plane.

$$\hbox{\epsfysize=1.75 in \epsffile{rev1-2.eps}}$$

The point $(4, -5, -1)$ is on the plane.

Therefore, the plane is

$$-(x - 4) + 4(y + 5) + (0)(z + 1) = 0, \quad\hbox{or}\quad -x + 4 y + 24 = 0.\quad\halmos$$

(c) Which contains the parallel lines

$$x = s, \quad y = 3 + 2 s, \quad z = 1 - 2 s,$$

$$x = 3 t, \quad y = 1 + 6 t, \quad z = 5 - 6 t.$$

First, I need a point on the plane. Since it contains both lines, a point on either line will do. Take $s = 0$ in the first line to obtain the point $P(0, 3, 1)$ .

Next, I need a vector perpendicular to the plane. The vector $(1, 2, -2)$ is parallel to the first line. For a second vector, I can't use a vector parallel to the second line, because the second line is parallel to the first. Instead, set $t = 0$ in the second line to obtain a point $Q(0, 1, 5)$ .

The vector $\bvec{P Q} = (0, -2, 4)$ goes from the first line to the second line, so it can't be parallel to either. Now I can take the cross product of the first line's vector $(1, 2, -2)$ with $\bvec{P Q} = (0, -2, 4)$ to get a vector perpendicular to the plane:

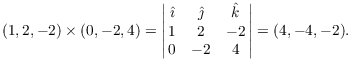
$$(1, 2, -2) \times (0, -2, 4) = \left|\matrix{ \ihat & \jhat & \khat \cr 1 & 2 & -2 \cr 0 & -2 & 4 \cr}\right| = (4, -4, -2).$$

Using the perpendicular vector $(4, -4, -2)$ together with the point $P(0, 3, 1)$ , I obtain the plane

$$4(x - 0) - 4(y - 3) - 2(z - 1) = 0, \quad\hbox{or}\quad 2 x - 2 y - z = -7.\quad\halmos$$

14. Find the point on the plane $2 x + y + 3 z = 6$ closest to the origin.

I'll do this by constructing a line which is perpendicular to the plane and passes through the origin. The desired point is the point where the line intersects the plane.

$$\hbox{\epsfysize=1.75 in \epsffile{rev1-3.eps}}$$

The vector $(2, 1, 3)$ is perpendicular to the plane. Hence, the following line passes through the origin and is perpendicular to the plane:

$$x = 2 t, \quad y = t, \quad z = 3 t.$$

Find the point where the line intersects the plane by substituting these expressions into the plane equation and solving for t:

$$2 \cdot 2 t + t + 3 \cdot 3 t = 6, \quad 14 t = 6, \quad t = \dfrac{3}{7}.$$

Finally, plugging this back into the x-y-z equations yields $x = \dfrac{6}{7}$ , $y = \dfrac{3}{7}$ , and $z = \dfrac{9}{7}$ . Hence, the point on the plane closest to the origin is $\left(\dfrac{6}{7},\dfrac{3}{7},\dfrac{9}{7} \right)$ .

15. Find the equation of the plane which goes through the point $(1, 3, -1)$ and is parallel to the plane $3 x - 2 y + 6 z = 9$ .

The vector $(3, -2, 6 )$ is perpendicular to $3 x - 2 y + 6 z = 9$ .

Since the plane I want to construct is parallel to the given plane, the vector $(3, -2, 6 )$ is perpendicular to the plane I want to construct.

$$\hbox{\epsfysize=1.75 in \epsffile{rev1-4.eps}}$$

The plane I want to construct contains the point $(1, 3, -1)$ .

Hence, the plane is

$$3(x - 1) - 2(y - 3) + 6(z + 1) = 0, \quad\hbox{or}\quad 3 x - 2 y + 6 z = -6.\quad\halmos$$

16. Find the equation of the line of intersection of the planes

$$2 x - 3 y + z = 0 \quad\hbox{and}\quad x + y + z = 4.$$

Set $z = t$ , then multiply the second equation by 3:

$$\matrix{ 2 x - 3 y + t = 0 & \rightarrow & 2 x - 3 y + t = 0 \cr x + y + t = 4 & \rightarrow & 3 x + 3 y + 3 t = 12 \cr}$$

Add the equations and solve for x:

$$5 x + 4 t = 12, \quad x = \dfrac{12}{5} - \dfrac{4}{5} t.$$

Plug this back tino $x + y + t = 4$ and solve for y:

$$\left(\dfrac{12}{5} - \dfrac{4}{5}t\right) + y + t = 4, \quad y = \dfrac{8}{5} - \dfrac{1}{5}t.$$

Therefore, the line of intersection is

$$x = \dfrac{12}{5} - \dfrac{4}{5}t, \quad y = \dfrac{8}{5} - \dfrac{1}{5}t, \quad z = t.$$

Note: You can also do this by taking vectors perpendicular to the two planes and computing their cross product. This gives a vector parallel to the line of intersection. Find a point on the line of intersection by setting $z = 0$ (say) and solving the plane equations simultaneously. Then plug the point and the cross product vector into the parametric equations for the line.

17. Find the distance from the point $(-6, 2, 3)$ to the plane $4 x - 5 y + 8 z = 7$ .

The vector $\vec v = (4, -5, 8)$ is perpendicular to the plane.

To find a point on the plane, set y and z equal to numbers (chosen at random) and solve for x. For example, set $y = 1$ and $z = 1$ . Then

$$4 x - 5 + 8 = 7, \quad\hbox{so}\quad 4 x = 4, \quad\hbox{or}\quad x = 1.$$

Thus, the point $Q(1, 1, 1)$ is on the plane. The vector from $P(-6, 2, 3)$ to Q is $(7, -1, -2)$ .

$$\hbox{\epsfysize=1.75 in \epsffile{rev1-5.eps}}$$

The distance is the absolute value of the component of $\bvec{PQ}$ in the direction of $\vec v$ :

$$\comp_{\vec v} \bvec{PQ} = \dfrac{(7, -1, -2) \cdot(4, -5, 8)} {\|(4, -5, 8)\|} = \dfrac{17}{\sqrt{105}} \approx 1.65703.\quad\halmos$$

18. (a) Show that the following lines intersect:

$$x = 2 + 3 t, \quad y = -4 - 2 t, \quad z = -1 + 4 t,$$

$$x = 6 + 4 s, \quad y = -2 + 2 s, \quad z = -3 - 2 s.$$

(b) Find the equation of the plane containing the two lines in part (a).

(a) Solve the x-equations simultaneously:

$$2 + 3 t = 6 + 4 s, \quad t = \dfrac{4}{3} + \dfrac{4}{3}s.$$

Set the y-expressions equal, then plug in $t = \dfrac{4}{3} + \dfrac{4}{3}s$ and solve for s:

$$-4 - 2 t = -2 + 2 s, \quad -4 - 2\left(\dfrac{4}{3} + \dfrac{4}{3}s\right) = -2 + 2 s, \quad -\dfrac{20}{3} - \dfrac{8}{3}s = -2 + 2 s, \quad s = -1.$$

Therefore, $t = \dfrac{4}{3} + \dfrac{4}{3}s = 0$ .

Check the values for consistency by plugging them into the z-equations:

$$z = -1 + 4 t = -1, \quad z = -3 - 2 s = -1.$$

The equations are consistent, so the lines intersect. If I plug $t = 0$ into the x-y-z equations, I obtain $x = 2$ , $y = -4$ , and $z = -1$ . The lines intersect at $(2, -4, -1)$ .

(b) The vector $(3, -2, 4)$ is parallel to the first line, and the vector $(4, 2, -2)$ is parallel to the second line. The cross product of the vectors is perpendicular to the plane containing the lines.

$$\hbox{\epsfysize=1.5 in \epsffile{rev1-6.eps}}$$

The cross product is

$$(3, -2, 4) \times(4, 2, -2) = \left|\matrix{\ihat & \jhat & \khat \cr 3 & -2 & 4 \cr 4 & 2 & -2 \cr}\right| = (-4, 22, 14).$$

From part (a), the point $(2, -4, -1)$ is on both lines, so it is surely in the plane. Therefore, the plane is

$$-4(x - 2) + 22(y + 4) + 14(z + 1) = 0, \quad\hbox{or}\quad -4 x + 22 y + 14 z = -110, \quad\hbox{or}\quad 2 x - 11 y - 7 z = 55.\quad\halmos$$

19. Find the distance between the skew lines

$$x = 3 + t, \quad y = 2 - 4 t, \quad z = t,$$

$$x = 4 - s, \quad y = 3 + s, \quad z = -2 + 3 s.$$

I'll find vectors $\vec{a}$ and $\vec{b}$ parallel to the lines and take their cross product. This gives a vector perpendicular to both lines. (If you think of the skew lines as lying in the ceiling and the floor of a room, the cross product vector $\vec{a}\times \vec{b}$ will be perpendicular to both the ceiling and the floor.)

Next, I'll find a point P on the first line and a point Q on the second line.

Finally, the distance between the lines --- in my analogy, the distance between the ceiling and the floor --- will be $|\comp_{\vec{a} \times \vec{b}} \bvec{P Q}|$ .

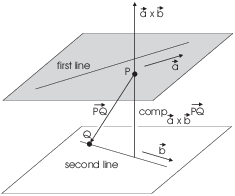
$$\hbox{\epsfysize=1.75 in \epsffile{rev1-7.eps}}$$

The vector $\vec{a} = (1, -4, 1)$ is parallel to the first line, and the vector $\vec{b} = (-1, 1, 3)$ is parallel to the second line. Hence, their cross product is

$$(1, -4, 1 ) \times (-1, 1, 3 ) = \left|\matrix{\ihat & \jhat & \khat \cr 1 & -4 & 1 \cr -1 & 1 & 3 \cr}\right| = (-13, -4, -3).$$

Setting $t = 0$ in the first line gives $x = 3$ , $y = 2$ , and $z = 0$ . Hence, the point $P(3, 2, 0)$ lies in the first line. Setting $s = 0$ in the second line gives $x = 4$ , $y = 3$ , and $z = -2$ , Hence, the point $Q(4, 3, -2)$ lies in the second line. The vector from one point to the other is $\bvec{PQ} = (1, 1, -2)$ .

Next,

$$\comp_{\vec{a} \times \vec{b}} \bvec{P Q} = \dfrac{(1, 1, -2) \cdot(-13, -4, -3)} {\|(-13, -4, -3)\|} = -\dfrac{11}{\sqrt{194}}.$$

Therefore, the distance is

$$\hbox{distance} = \dfrac{11}{\sqrt{194}} = 0.78975 \ldots.\quad\halmos$$

20. (a) Parametrize the segment from $P(2, -3, 5)$ to $Q(-10, 0, 6)$ .

(b) Parametrize the curve of intersection of the paraboloid $z = x^2 + y^2$ and the plane $2 x - 4 y + z = 4$ .

(c) Parametrize the curve of intersection of the cylinder $x^2 + 4 y^2 = 25$ with the plane $x - 3 y + z = 7$ .

(a)

$$(x, y, z) = (1 - t)(2, -3, 5) + t(-10, 0, 6) = (2 - 12 t, -3 + 3 t, 5 + t),$$

$$x = 2 - 12 t, \quad y = -3 + 3 t, \quad z = 5 + t \quad\hbox{for}\quad 0 \le t \le 1.\quad\halmos$$

(b) Solving the plane equation for z gives $z = 4 - 2 x + 4 y$ . Equate the two expressions for z, then complete the square in x and y:

$$x^2 + y^2 = 4 - 2 x + 4 y, \quad x^2 + 2 x + y^2 - 4 y = 4, \quad x^2 + 2 x + 1 + y^2 - 4 y + 4 = 9, \quad (x + 1)^2 + (y - 2)^2 = 9.$$

This equation represents the projection of the curve of intersection into the x-y plane. It's a circle with center $(-1, 2)$ and radius 3. It may be parametrized by

$$x = 3(\cos t - 1), \quad y = 3(\sin t + 2).$$

Plug this back into either z-equation to find z. I'll use the plane equation:

$$z = 4 - 2\left(3(\cos t - 1)\right) + 4\left(3(\sin t + 2)\right) = 34 - 6\cos t + 12\sin t.$$

The curve of intersection is

$$x = 3(\cos t - 1), \quad y = 3(\sin t + 2), \quad z = 34 - 6\cos t + 12 \sin t.\quad\halmos$$

(c) The curve $x^2 + 4 y^2 = 25$ may be parametrized by

$$x = 5 \cos t, \quad y = \dfrac{5}{2} \sin t.$$

Solving the plane equation for z yields $z = 7 - x + 3 y$ . Plug in the expressions for x and y:

$$z = 7 - 5 \cos t + \dfrac{15}{2} \sin t.$$

The curve of intersection is

$$x = 5 \cos t, \quad y = \dfrac{5}{2} \sin t, \quad z = 7 - 5 \cos t + \dfrac{15}{2} \sin t.\quad\halmos$$

21. (a) Parametrize the surface $x^2 + y^2 + 4 z^2 = 9$ .

(b) Parametrize the surface $x^2 + y^2 = 7$ .

(c) Parametrize the surface generated by revolving the curve $y = \sin x$ about the x-axis.

(d) Parametrize the surface $y = x^3 + 3 x z - z^2$ .

(e) Parametrize the parallelogram having $P(5, -4, 7)$ as a vertex, where $\vec{v} = (3, 3, 0)$ and $\vec{w} = (8, -1, 3)$ are the sides of the parallelogram which emanate from P.

(f) Parametrize the part of the surface $y = x^2$ lying between the x-y-plane and $z = x + 2 y + 3$ .

(a) Without the "4", this would be $x^2 + y^2 + z^2 = 9$ , a sphere of radius 3 centered at the origin. The standard parametrization for $x^2 + y^2 + z^2 = 9$ is

$$x = 3 \cos u \cos v, \quad y = 3 \sin u \cos v, \quad z = 3 \sin v.$$

The account for the "4", I multiply the z-term by $\dfrac{1}{2}$ , since $\left(\dfrac{1}{2}\right)^2 = \dfrac{1}{4}$ and this cancels the "4":

$$x = 3 \cos u \cos v, \quad y = 3 \sin u \cos v, \quad z = \dfrac{3}{2}\sin v.\quad\halmos$$

(b) I can use a circle parametrization for $x^2 + y^2 = 7$ and a separate parameter for z:

$$x = \sqrt{7} \cos u, \quad y = \sqrt{7} \sin u, \quad z = v.\quad\halmos$$

(c) The curve $y = \sin x$ may be parametrized by

$$x = u, \quad y = \sin u.$$

Therefore, the surface generated by revolving the curve $y = \sin x$ about the x-axis may be parametrized by

$$x = u, \quad y = \sin u \cos v, \quad z = \sin u \sin v.\quad\halmos$$

(d) Simply set the independent variables x and z equal to parameters u and v, then plug into the given equation to find y:

$$x = u, \quad y = u^3 + 3 u v - v^2, \quad z = v.\quad\halmos$$

(e) Use the given vectors as columns of the coefficient matrix, then add the basepoint:

$$\left[\matrix{x \cr y \cr z \cr}\right] = \left[\matrix{3 & 8 \cr 3 & -1 \cr 0 & 3 \cr}\right] \left[\matrix{u \cr v \cr}\right] + \left[\matrix{5 \cr -4 \cr 7 \cr}\right], \quad\hbox{or}\quad x = 3 u + 8 v + 5, \quad y = 3 u - v - 4, \quad z = 3 v + 7.$$

The parameter ranges are $0 \le u \le 1$ and $0 \le v \le 1$ .

(f) I'll use a segment parametrization. The curve $y = x^2$ may be parametrized by

$$x = u, \quad y = u^2.$$

Thus, a typical point on the intersection of the surface $y = x^2$ with the x-y-plane has coordinates $(u, u^2, 0)$ , since the x-y-plane is $z = 0$ .

Plugging $x = u$ and $y = u^2$ into $z = x + 2 y + 3$ yields $z = u + 2 u^2 + 3$ . Therefore, the point on the plane $z = x + 2 y + 3$ which lies directly above $(u, u^2, 0)$ is $(u, u^2, u + 2 u^2 + 3)$ .

The segment joining $(u, u^2, 0)$ to $(u, u^2, u + 2 u^2 + 3)$ is

$$(x, y, z) = (1 - v)(u, u^2, 0) + v(u, u^2, u + 2 u^2 + 3) = (u, u^2, 3 v + u v + 2 u^2 v).$$

Therefore, the surface may be parametrized by

$$x = u, \quad y = u^2, \quad z = 3 v + u v + 3 u^2 v, \quad\hbox{where}\quad 0 \le v \le 1.\quad\halmos$$

22. Let

$$g(t) = (7 t^2 + 13 t + 4, 110, 6 t - e^{2 t}).$$

Compute $g'(t)$ and $g'(1)$ .

$$g'(t) = (14 t + 13, 0, 6 - 2 e^{2 t}) \quad\hbox{and}\quad g'(0) = (13, 0, 4).\quad\halmos$$

23. The position of a cheesesteak stromboli at time t is

$$\vec{f}(t) = (e^{t^2}, \ln (t^2 + 1), \tan t).$$

(a) Find the velocity and acceleration of the stromboli at $t = 1$ .

(b) Find the speed of the stromboli at $t = 1$ .

(a)

$$\vec{v}(t) = \vec{f}\,'(t) = \left(2 te^{t^2}, \dfrac{2 t}{t^2 + 1}, (\sec t)^2\right),$$

$$\vec{a}(t) = \vec{v}\,'(t) = \left(4 t^2 e^{t^2} + 2 e^{t^2}, \dfrac{(t^2 + 1)(2) - (2 t)(2 t)}{(t^2 + 1)^2}, 2(\sec t)^2\tan t\right).$$

Hence,

$$\vec{v}(1) = (2 e, 1, (\sec 1)^2) \quad\hbox{and}\quad \vec{a}(1) = \left(6 e, 0, 2(\sec 1)^2\tan 1\right).\quad\halmos$$

(b)

$$\|\vec{v}(1)\| = \sqrt{(2 e)^2 + 1^2 + ((\sec 1)^2)^2} = \sqrt{4 e^2 + 1 + (\sec 1)^4}.\quad\halmos$$

24. The acceleration of a cheeseburger at time t is

$$\vec{a}(t) = (6 t, 4, 4 e^{2 t}).$$

Find the position $\vec{f}(t)$ if $\vec{v}(1) = (5, 6, 2 e^2 - 3)$ and $\vec{f}(0) = (1, 3, 2)$ .

Since the acceleration function is the derivative of the velocity function, the velocity function is the integral of the acceleration function:

$$\vec{v}(t) = \int (6 t, 4, 4 e^{2 t})\,dt = \left(3 t^2, 4 t, 2 e^{2 t}\right) + (c_1, c_2, c_3).$$

In order to find the arbitrary constant vector $(c_1, c_2, c_3)$ , I'll plug the initial condition $\vec{v}(1) = (5, 6, 2 e^2 - 3)$ into the equation for $\vec{v}(t)$ :

$$(5, 6, 2 e^2 - 3) = \vec{v}(1) = (3, 4, 2 e^2) + (c_1, c_2, c_3), \quad (2, 2, -3) = (c_1, c_2, c_3).$$

Therefore,

$$\vec{v}(t) = \left(3 t^2, 4 t, 2 e^{2 t}\right) + (2, 2, -3) = \left(3 t^2 + 2, 4 t + 2, 2 e^{2 t} - 3\right).$$

Since the velocity function is the derivative of the position function, the position function is the integral of the velocity function:

$$\vec{f}(t) = \int \left(3 t^2 + 2, 4 t + 2, 2 e^{2 t} - 3\right)\,dt = \left(t^3 + 2 t, 2 t^2 + 2 t, e^{2 t} - 3 t\right) + (d_1, d_2, d_3).$$

In order to find the arbitrary constant vector $(d_1, d_2, d_3)$ , I'll plug the initial condition $\vec{f}(0) = (1, 3, 2)$ into the equation for $\vec{f}(t)$ :

$$(1, 3, 2) = \vec{f}(0) = (0, 0, 1) + (d_1, d_2, d_3), \quad (1, 3, 1) = (d_1, d_2, d_3).$$

Therefore,

$$\vec{f}(t) = \left(t^3 + 2 t, 2 t^2 + 2 t, e^{2 t} - 3 t\right) + (1, 3, 1) = \left(t^3 + 2 t + 1, 2 t^2 + 2 t + 3, e^{2 t} - 3 t + 1\right).\quad\halmos$$

25. Compute $\displaystyle \int \left(t^2\cos 2 t, t^2 e^{t^3}, \dfrac{1}{\sqrt{t}}\right)\,dt$ .

I'll compute the integral of each component separately.

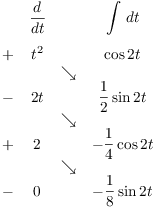
$$\matrix{& \der {} t & & \displaystyle \int\,dt \cr & & & \cr + & t^2 & & \cos 2 t \cr & & \searrow & \cr - & 2 t & & \dfrac{1}{2}\sin 2 t \cr & & \searrow & \cr + & 2 & & -\dfrac{1}{4}\cos 2 t \cr & & \searrow & \cr - & 0 & & -\dfrac{1}{8}\sin 2 t \cr}$$

$$\int t^2\cos 2 t\,dt = \dfrac{1}{2}t^2\sin 2 t + \dfrac{1}{2}t\cos 2 t - \dfrac{1}{4}\sin 2 t + C.$$

$$\int t^2 e^{t^3}\,dt = \int t^2 e^u\cdot \dfrac{du}{3 t^2} = \dfrac{1}{3} \int e^u\,du = \dfrac{1}{3}e^u + C = \dfrac{1}{3}e^{t^3} + C.$$

$$\left[u = t^3, \quad du = 3 t^2\,dt, \quad dt = \dfrac{du}{3 t^2}\right]$$

$$\int \dfrac{1}{\sqrt{t}}\,dt = 2\sqrt{t} + C.$$

Therefore,

$$\int \left(t^2\cos 2 t, t^2 e^{t^3}, \dfrac{1}{\sqrt{t}}\right)\,dt = \left(\dfrac{1}{2}t^2\sin 2 t + \dfrac{1}{2}t\cos 2 t - \dfrac{1}{4}\sin 2 t, \dfrac{1}{3}e^{t^3}, 2\sqrt{t}\right) + \vec{c}.\quad\halmos$$

26. Find the length of the curve

$$x = \dfrac{1}{2}t^2 + 1, \quad y = \dfrac{8}{3}t^{3/2} + 1, \quad z = 8 t - 2, \quad 0 \le t \le 1.$$

$$\der x t = t, \quad \der y t = 4 t^{1/2}, \quad \der z t = 8,$$

$$\left(\der x t\right)^2 = t^2, \quad \left(\der y t\right)^2 = 16 t, \quad \left(\der z t\right)^2 = 64,$$

$$\sqrt{\left(\der x t\right)^2 + \left(\der y t\right)^2 + \left(\der z t\right)^2} = \sqrt{t^2 + 16 t + 64} = \sqrt{(t + 8)^2} = t + 8.$$

The length of the curve is

$$L = \int_0^1 (t + 8)\,dt = \left[\dfrac{1}{2}t^2 + 8 t\right]_0^1 = \dfrac{17}{2}.\quad\halmos$$

27. Find the unit tangent vector to:

(a) $\vec{f}(t) = \left(t^2 + t + 1, \dfrac{1}{t}, \sqrt{6} t\right)$ at $t = 1$ .

(b) $\vec{f}(t) = (\cos 5 t, \sin 5 t, 3 t)$ .

(a)

$$\vec{f}\,'(t) = \left(2 t + 1, -\dfrac{1}{t^2}, \sqrt{6}\right), \quad\hbox{so}\quad \vec{f}\,'(1) = (3, -1, \sqrt{6}).$$

Since $\|\vec{f}\,'(1)\| = \sqrt{9 + 1 + 6} = 4$ , the unit tangent vector is

$$\vec{T}(1) = \dfrac{\vec{f}\,'(1)}{\|\vec{f}\,'(1)\|} = \dfrac{1}{4}(3, -1,\sqrt{6}).\quad\halmos$$

(b)

$$\vec{f}\,'(t) = (-5\sin 5 t, 5\cos 5 t, 3),$$

$$\|\vec{f}\,'(t)\| = \sqrt{(-5\sin 5 t)^2 + (5\cos 5 t)^2 + 3^2} = \sqrt{25(\sin 5 t)^2 + 25(\cos 5 t)^2 + 9} = \sqrt{25 + 9} = \sqrt{34}.$$

Hence, the unit tangent vector is

$$\vec{T}(t) = \dfrac{\vec{f}\,'(t)}{\|\vec{f}\,'(t)\|} = \dfrac{1}{\sqrt{34}}(-5\sin 5 t, 5\cos 5 t, 3).\quad\halmos$$

28. Find the curvature of:

(a) $y = \tan x$ at $x = \dfrac{\pi}{4}$ .

(b) $\vec{f}(t) = (t^2 + 1, 5 t + 1, 1 - t^3)$ at $t = 1$ .

(a) Since $y = \tan x$ is a curve in the x-y-plane, I'll use the formula

$$\kappa = \dfrac{|f''(x)|}{(1 + f'(x)^2)^{3/2}}.$$

First,

$$f'(x) = (\sec x)^2 \quad\hbox{and}\quad f''(x) = 2(\sec x)^2\tan x.$$

Plug in $x = \dfrac{\pi}{4}$ :

$$f'\left(\dfrac{\pi}{4}\right) = (\sqrt{2})^2 = 2, \quad f''\left(\dfrac{\pi}{4}\right) = 2(\sqrt{2})^2(1) = 4.$$

The curvature is

$$\kappa = \dfrac{|4|}{(1 + 2^2)^{3/2}} = \dfrac{4}{5\sqrt{5}}.\quad\halmos$$

(b) In this case, I'll use the formula

$$\kappa = \dfrac{\|\vec{f}\,'(t) \times \vec{f}\,''(t)\|}{\|\vec{f}\,'(t)\|^3}.$$

First,

$$\vec{f}\,'(t) = (2 t, 5, 3 t^2) \quad\hbox{and}\quad \vec{f}\,''(t) = (2, 0, 6 t).$$

Hence,

$$\vec{f}\,'(1) = (2, 5, 3) \quad\hbox{and}\quad \vec{f}\,''(1) = (2, 0, 6).$$

Next,

$$\vec{f}\,'(1) \times \vec{f}\,''(1) = \left|\matrix{\ihat & \jhat & \khat \cr 2 & 5 & 3 \cr 2 & 0 & 6 \cr}\right| = (30, -6, -10).$$

The curvature is

$$\kappa = \dfrac{\|(30, -6, -10)\|} {\|(2, 5, 3)\|^3} = \dfrac{\sqrt{900 + 36 + 100}}{(\sqrt{4 + 25 + 9})^3} = \dfrac{\sqrt{1036}}{38 \sqrt{38}}.\quad\halmos$$

29. Find the unit tangent and unit normal for the curve $y = \dfrac{1}{3}x^3 + x^2 + 3 x + \dfrac{2}{3}$ at the point $(1, 5)$ .

The curve may be parametrized by

$$\vec{f}(t) = \left(t, \dfrac{1}{3}t^3 + t^2 + 3 t + \dfrac{2}{3}\right).$$

Thus,

$$\vec{f}\,'(t) = (1, t^2 + 2 t + 3), \quad \vec{f}\,'(1) = (1, 6), \quad \|\vec{f}\,'(1)\| = \sqrt{37}.$$

The unit tangent is

$$\vec{T}(1) = \dfrac{1}{\sqrt{37}}(1, 6).$$

For a plane curve, I can use geometry to find the unit normal. By swapping components and negating one of them, I can see that the following unit vectors are perpendicular to $\vec{T}(1)$ :

$$\dfrac{1}{\sqrt{37}}(-6, 1), \quad \dfrac{1}{\sqrt{37}}(6, -1).$$

Graph the curve near $x = 1$ :

$$\hbox{\epsfysize=1.75 in \epsffile{rev1-8.eps}}$$

From the graph, I can see that the unit normal at $x = 1$ must point up and to the left. This means that the x-component must be negative and the y-component must be positive. Hence,

$$\vec{N}(1) = \dfrac{1}{\sqrt{37}}(-6, 1).$$

Note that you can't use this trick in 3 dimensions, since there are infinitely many vectors perpendicular to the unit tangent.

30. Find the unit tangent, the unit normal, the binormal, and the osculating circle at $t = 1$ for the curve

$$\vec{f}(t) = \left(\dfrac{1}{3}t^3 + 1, t^2 + 1, 2 t + 5\right).$$

$$\vec{f}\,'(t) = (t^2, 2 t, 2), \quad \vec{f}\,'(1) = (1, 2, 2), \quad \|\vec{f}\,'(1)\| = 3.$$

The unit tangent at $t = 1$ is

$$\vec{T}(1) = \dfrac{1}{3}(1, 2, 2).$$

Now

$$\|\vec{f}\,'(t)\| = \sqrt{t^4 + 4 t^2 + 4} = \sqrt{(t^2 + 2)^2} = t^2 + 2,$$

so

$$\vec{T}(t) = \left(\dfrac{t^2}{t^2 + 2}, \dfrac{2 t}{t^2 + 2}, \dfrac{2}{t^2 + 2}\right).$$

Hence,

$$\vec{T}\,'(t) = \left(\dfrac{4 t}{(t^2 + 2)^2}, \dfrac{4 - 2 t^2}{(t^2 + 2)^2}, -\dfrac{4 t}{(t^2 + 2)^2}\right),$$

$$\vec{T}\,'(1) = \left(\dfrac{4}{9}, \dfrac{2}{9}, -\dfrac{4}{9}\right) = \dfrac{2}{9}(2, 1, -2),$$

$$\|\vec{T}\,'(1)\| = \dfrac{2}{9}\sqrt{2^2 + 1^2 + (-2)^2} = \dfrac{2}{3}.$$

The unit normal at $t = 1$ is

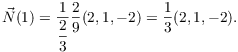
$$\vec{N}(1) = \dfrac{1}{\dfrac{2}{3}}\dfrac{2}{9} (2, 1, -2) = \dfrac{1}{3}(2, 1, -2).$$

The binormal at $t = 1$ is

$$\vec{B}(1) = \vec{T}(1) \times \vec{N}(1) = \dfrac{1}{9}\left|\matrix{ \ihat & \jhat & \khat \cr 1 & 2 & 2 \cr 2 & 1 & -2 \cr}\right| = \dfrac{1}{9} (-6, 6, -3) = \dfrac{1}{3} (-2, 2, -1).$$

Next, I'll compute the curvature.

$$\vec{f}\,'(t) = (t^2, 2 t, 2), \quad\hbox{so}\quad \vec{f}\,''(t) = (2 t, 2, 0), \quad\hbox{and}\quad \vec{f}\,''(1) = (2, 2, 0).$$

So

$$\vec{f}\,'(1)\times \vec{f}\,''(1) = \left|\matrix{\ihat & \jhat & \khat \cr 1 & 2 & 2 \cr 2 & 2 & 0 \cr}\right| = (-4, 4, -2) \quad\hbox{and}\quad \|\vec{f}\,'(1)\times \vec{f}\,''(1)\| = \sqrt{16 + 16 + 4} = 6.$$

The curvature is

$$\kappa = \dfrac{\|\vec{f}\,'(1)\times \vec{f}\,''(1)\|} {\|\vec{f}\,'(1)\|^3} = \dfrac{6}{3^3} = \dfrac{2}{9}.$$

The point on the curve is $\vec{f}(1) = \left(\dfrac{4}{3}, 2, 7\right)$ . Therefore the equation of the osculating circle is

$$(x, y, z) = \left(\dfrac{4}{3}, 2, 7\right) + \dfrac{9}{2}\cdot \dfrac{1}{3}(2, 1, -2) + \dfrac{9}{2}\cdot \dfrac{1}{3}(1, 2, 2)\cos t + \dfrac{9}{2}\cdot \dfrac{1}{3}(2, 1, -2)\sin t =$$

$$\left(\dfrac{13}{3} + \dfrac{3}{2}\cos t + 3\sin t, \dfrac{7}{2} + 3\cos t + \dfrac{3}{2}\sin t, 4 + 3\cos t - 3\sin t\right).\quad\halmos$$

Tell me what you think you are and I will tell you what you are not. - Henri Frédéric Amiel

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga