Review Problems for Test 3

Math 311

These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the absence of a topic does not imply that it won't appear on the test.

1. Compute the exact value of $\displaystyle \int_0^2 \int_0^{1 + \sqrt{2 x - x^2}}\,dy\,dx$ .

2. Compute the exact value of $\displaystyle \int_{-4}^4 \int_{-\sqrt{16 - x^2}}^{\sqrt{16 - x^2}} \int_{\sqrt{x^2 + y^2}}^4 \,dz\,dy\,dx$ .

3. Find the volume of the solid lying below the paraboloid $z = x^2 + y^2$ and above the region in the x-y plane bounded by $y = x^2$ and $y = x + 2$ .

4. Compute $\displaystyle \int_0^1 \int_{\sqrt{y}}^1 \dfrac{1}{\sqrt{x^3 + 4}}\,dx\,dy$ .

5. Compute

$$\int_0^2 \int_{y/2}^1 3 y^2 \cos (x^4)\,dx\,dy + \int_{-2}^0 \int_{-y/2}^1 3 y^2 \cos (x^4)\,dx\,dy.$$

6. Compute $\displaystyle \int_0^2 \int_{-\sqrt{2 x - x^2}}^{\sqrt{2 x - x^2}} \sqrt{x^2 + y^2}\,dy\,dx$ .

7. Find the volume of the region which lies above the cone $z = \dfrac{1}{\sqrt{3}}\sqrt{x^2 + y^2}$ and below the hemisphere $z = \sqrt{1 - x^2 - y^2}$ .

8. Compute $\displaystyle \int_0^1 \int_0^{\sqrt{1 - x^2}} \int_0^{x + y} \sqrt{x^2 + y^2}\,dz\,dy\,dx$ .

9. Find the area of the part of the surface $z = 9 - x^2 - y^2$ which lies inside the cylinder $x^2 + y^2 = 1$ .

10. Find the area of the surface

$$x = 2 u \cos v, \quad y = u^2, \quad z = 2 u \sin v, \quad 0 \le u \le 1, \quad 0 \le v \le 2 \pi.$$

11. A lamina occupies the region in the x-y-plane bounded above by $y = 1$ and below by $y = x^2$ . The density is $\delta(x, y) = y + 1$ . Find the coordinates of the center of mass.

12. Let R be the region between $z = 2 x^2 + 2 y^2$ and $z = x^2 + y^2 + 4$ . Find the centroid of R.

13. Compute $\displaystyle \dint_R (x - 2 y)\,dx\,dy$ , where R is the parallelogram with vertices $A(0, 1)$ , $B(2, 0)$ , $C(4, 2)$ , $D(2, 3)$ (counterclockwise).

14. (a) Let R be the region in the first quadrant bounded above by $y = 2 - x^2$ and bounded below by $y = 1 - x^2$ , from $x = 0$ to $x = 1$ . Find a transformation which carries the square

$$\left\{\matrix{ 0 \le u \le 1 \cr 0 \le v \le 1 \cr}\right\} \quad\hbox{onto}\quad R.$$

(b) Use a change of variables to evaluate

$$\dint_R (4 x^2 + y)\,dx\,dy.$$

15. Let $f(x, y, z) = 3 x + y$ , and let

$$\vec{\sigma}(t) = \left(\dfrac{1}{3} t^3 + 1, 8 t - 3, 2 t^2\right), \quad 0 \le t \le 1.$$

Compute $\displaystyle \int_{\vec{\sigma}} f\,ds$ .

16. Compute $\displaystyle \int_{\vec{\sigma}} (x + y)\,dx - (x - y)\,dy$ , where $\sigma$ is the path consisting of the segment from $(0, 1)$ to $(-1, 0)$ , the segment from $(-1, 0)$ to $(0, -1)$ , the segment from $(0, -1)$ to $(1, 0)$ , and the segment from $(1, 0)$ to $(0, 1)$ .

17. Compute $\displaystyle \int_{\vec{\sigma}} \vec{F} \cdot \bvec{ds}$ , where $\vec{\sigma}$ is the curve of intersection of $x^2 + y^2 = 1$ and the plane $z = 2 + 2 x + 3 y$ , traversed counterclockwise as viewed from above, and $\vec{F} = (-2 y, 2 x, 2)$ .

18. Let $\vec{F}(x, y, z) = (x^2 y + z, x z, x + 3 y z)$ . Compute $\curl \vec{F}$ and $\diverg \vec{F}$ .

19. Let $\vec{\sigma}(t)$ be the path which consists of the curve $\left(\dfrac{3 t}{2 t + 1}, t e^{2 (t - 1)}, \dfrac{1}{8} t^2 (t^2 + 1)^3\right)$ for $ 0 \le t \le 1$ , followed by the segment from $(1, 1, 1)$ to $(1, 2, -1)$ .

Compute

$$\int_{\vec{\sigma}} (y^2 + z^3)\,dx + (2 x y - 2 y)\,dy + (3 x z^2 + 4)\,dz,$$

20. Let $\vec{\sigma}$ be the boundary of the square $0 \le x \le 1$ , $0 \le y \le 1$ , traversed in the counterclockwise direction.

Compute

$$\int_{\vec{\sigma}} (x^2 y - x y^2)\,dx + \left(2 x^2 y + \dfrac{1}{3} x^3\right)\,dy.$$

21. Let $\vec{\sigma}$ be the boundary of the region bounded below by $y = x^2$ and above by $y = 4$ , traversed counterclockwise. Compute

$$\int_{\vec{\sigma}} (4 x y - 2 y^2)\,dx + (2 x^2 + y^4)\,dy.$$

22. Find the area of the region enclosed by the ellipse

$$\dfrac{x^2}{4} + \dfrac{y^2}{9} = 1.$$

Solutions to the Review Problems for Test 3

1. Compute the exact value of $\displaystyle \int_0^2 \int_0^{1 + \sqrt{2 x - x^2}}\,dy\,dx$ .

Rewrite $y = 1 + \sqrt{2 x - x^2}$ :

$$\eqalign{ y - 1 & = \sqrt{2 x - x^2} \cr (y - 1)^2 & = 2 x - x^2 \cr x^2 - 2 x + (y - 1)^2 & = 0 \cr x^2 - 2 x + 1 + (y - 1)^2 & = 1 \cr (x - 1)^2 + (y - 1)^2 & = 1 \cr}$$

Thus, $y = 1 + \sqrt{2 x - x^2}$ is the top half of the circle of radius 1 centered at $(1, 1)$ . The region is bounded above by this semicircle, below by the x-axis, and on the sides by $x = 0$ and $x = 2$ :

$$\hbox{\epsfysize=1.75 in \epsffile{rev3-1.eps}}$$

Since the integrand is 1, the integral represents the area of the region. The area is the sum of the area of the semicircle (which has radius 1) and the rectangle below it (which is 2 by 1). Thus,

$$\int_0^2 \int_0^{1 + \sqrt{2 x - x^2}}\,dy\,dx = \dfrac{1}{2} \pi \cdot 1^2 + 2 \cdot 1 = 2 + \dfrac{\pi}{2}.\quad\halmos$$

2. Compute the exact value of $\displaystyle \int_{-4}^4 \int_{-\sqrt{16 - x^2}}^{\sqrt{16 - x^2}} \int_{\sqrt{x^2 + y^2}}^4 \,dz\,dy\,dx$ .

The projection of the region into the x-y plane is

$$\left\{\matrix{ -4 \le x \le 4 \cr -\sqrt{16 - x^2} \le y \le \sqrt{16 - x^2} \cr}\right\}$$

This is the circle of radius 4 centered at the origin.

The bottom of the region is the cone $z = \sqrt{x^2 + y^2}$ and the top is the plane $z = 4$ .

$$\hbox{\epsfysize=1.75 in \epsffile{rev3-2.eps}}$$

Thus, the region is a cone with height $h = 4$ and radius $r = 4$ .

Since the integrand is 1, the integral represent the volume of the region. A cone of height h and radius r has volume $\dfrac{1}{3}\pi r^2 h$ . Therefore,

$$\int_{-4}^4 \int_{-\sqrt{16 - x^2}}^{\sqrt{16 - x^2}} \int_{\sqrt{x^2 + y^2}}^4\,dz\,dy\,dx = \dfrac{1}{3} \pi \cdot 4^2 \cdot 4 = \dfrac{64 \pi}{3}.\quad\halmos$$

3. Find the volume of the solid lying below the paraboloid $z = x^2 + y^2$ and above the region in the x-y plane bounded by $y = x^2$ and $y = x + 2$ .

The projection into the x-y plane is:

$$\hbox{\epsfysize=1.75 in \epsffile{rev3-3.eps}}$$

Since $x^2$ and $x + 2$ intersect at $x = -1$ and at $x = 2$ , the region is described by the following inequalities:

$$\left\{\matrix{ -1 \le x \le 2 \cr x^2 \le y \le x + 2 \cr}\right\}$$

The top of the solid is $z = x^2 + y^2$ . The bottom is the x-y plane $z = 0$ . The picture below shows the top and the bottom; the solid is the region between them.

$$\hbox{\epsfysize=1.75 in \epsffile{rev3-4.eps}}$$

The volume is

$$\int_{-1}^2 \int_{x^2}^{x+2} (x^2 + y^2)\,dy\,dx = \int_{-1}^2 \left[x^2 y + \dfrac{1}{3} y^3\right]_{x^2}^{x + 2}\,dx = \int_{-1}^2 \left(x^3 + 2 x^2 + \dfrac{1}{3} (x + 2)^3 - x^4 - \dfrac{1}{3}x^6\right)\,dx =$$

$$\left[\dfrac{1}{4} x^4 + \dfrac{2}{3} x^3 + \dfrac{1}{12} (x + 2)^4 - \dfrac{1}{5} x^5 - \dfrac{1}{21} x^7\right]_{-1}^2 = \dfrac{639}{35} = 18.25714 \ldots.\quad\halmos$$

4. Compute $\displaystyle \int_0^1 \int_{\sqrt{y}}^1 \dfrac{1}{\sqrt{x^3 + 4}}\,dx\,dy$ .

Interchange the order of integration:

$$\raise0.8 in \hbox{$\left\{\matrix{0 \le y \le 1 \cr \sqrt{y} \le x \le 1 \cr}\right\} \quad\to\quad $} \hbox{\epsfysize=1.75 in \epsffile{rev3-5.eps}} \raise0.8 in \hbox{$\quad\to\quad \left\{\matrix{0 \le x \le 1 \cr 0 \le y \le x^2 \cr}\right\}$}$$

Thus,

$$\int_0^1 \int_{\sqrt{y}}^1 \dfrac{1}{\sqrt{x^3 + 4}}\,dx\,dy = \int_0^1 \int_0^{x^2} \dfrac{1}{\sqrt{x^3 + 4}}\,dy\,dx = \int_0^1 \dfrac{1}{\sqrt{x^3 + 4}} \left[y\right]_0^{x^2}\,dx = \int_0^1 \dfrac{x^2}{\sqrt{x^3 + 4}}\,dx =$$

$$\left[\dfrac{2}{3}(x^3 + 4)^{1/2}\right]_0^1 = \dfrac{2}{3}(\sqrt{5} - 2) = 0.15737 \ldots.$$

Here's the work for the integral:

$$\int \dfrac{x^2}{\sqrt{x^3 + 4}}\,dx = \int \dfrac{x^2}{\sqrt{u}}\cdot \dfrac{du}{3 x^2} = \dfrac{1}{3} \int \dfrac{du}{\sqrt{u}} = \dfrac{2}{3}\sqrt{u} + c = \dfrac{2}{3}\sqrt{x^3 + 4} + c.$$

$$\left[u = x^3 + 4, \quad du = 3 x^2\,dx, \quad dx = \dfrac{du}{3 x^2}\right]\quad\halmos$$

5. Compute

$$\int_0^2 \int_{y/2}^1 3 y^2 \cos (x^4)\,dx\,dy + \int_{-2}^0 \int_{-y/2}^1 3 y^2 \cos (x^4)\,dx\,dy.$$

Interchange the order of integration:

$$\left\{\matrix{ 0 \le y \le 2 \cr \dfrac{y}{2} \le x \le 1 \cr}\right\} \hskip0.5in \left\{\matrix{ -2 \le y \le 0 \cr -\dfrac{y}{2} \le x \le 1 \cr}\right\}$$

$$\hbox{\epsfysize=1.75 in \epsffile{rev3-6.eps}}$$

$$\left\{\matrix{ 0 \le x \le 1 \cr -2 x \le y \le 2 x \cr}\right\}$$

Thus,

$$\int_0^2 \int_{y/2}^1 3 y^2 \cos (x^4)\,dx\,dy + \int_{-2}^0 \int_{-y/2}^1 3 y^2 \cos (x^4)\,dx\,dy = \int_0^1 \int_{-2 x}^{2 x} 3 y^2 \cos (x^4)\,dy\,dx =$$

$$\int_0^1 \cos (x^4) \left[y^3\right]_{-2 x}^{2 x}\,dx = 16 \int_0^1 x^3 \cos (x^4)\,dx = 4 \left[\sin (x^4)\right]_0^1 = 4 \sin 1 = 3.36588 \ldots.$$

Here's the work for the integral:

$$\int x^3 \cos (x^4)\,dx = \int x^3 \cos u \cdot \dfrac{du}{4 x^3} = \dfrac{1}{4} \int \cos u\,du = \dfrac{1}{4} \sin u + c = \dfrac{1}{4} \sin (x^4) + c.$$

$$\left[u = x^4, \quad du = 4 x^3\,dx, \quad dx = \dfrac{du}{4 x^3}\right]\quad\halmos$$

6. Compute $\displaystyle \int_0^2 \int_{-\sqrt{2 x - x^2}}^{\sqrt{2 x - x^2}} \sqrt{x^2 + y^2}\,dy\,dx$ .

Note that $y = \pm \sqrt{2 x - x^2}$ may be rewritten as follows:

$$\eqalign{ y^2 & = 2 x - x^2 \cr x^2 - 2 x + y^2 & = 0 \cr x^2 - 2 x + 1 + y^2 & = 1 \cr (x - 1)^2 + y^2 & = 1 \cr}$$

This is a circle of radius 1 centered at $(1, 0)$ .

I'll convert to polar:

$$\left\{\matrix{ 0 \le x \le 2 \cr -\sqrt{2 x - x^2} \le y \le \sqrt{2 x - x^2} \cr}\right\}$$

$$\hbox{\epsfysize=1.75 in \epsffile{rev3-7.eps}}$$

$$\left\{\matrix{ -\dfrac{\pi}{2} \le \theta \le \dfrac{\pi}{2} \cr 0 \le r \le 2\cos \theta \cr}\right\}$$

To get the polar equation for the circle, start with $x^2 - 2 x + y^2 = 0$ . Then

$$\eqalign{ x^2 + y^2 & = 2 x \cr r^2 & = 2 r \cos \theta \cr r & = 2 \cos \theta \cr}$$

Note that the whole circle is traced out once as $\theta$ goes from $-\dfrac{\pi}{2}$ to $\dfrac{\pi}{2}$ (not, for example, from 0 to $2 \pi$ ).

The integrand is $\sqrt{x^2 + y^2} = \sqrt{r^2} = r$ . So

$$\int_0^2 \int_{-\sqrt{2 x - x^2}}^{\sqrt{2 x - x^2}} \sqrt{x^2 + y^2}\,dy\,dx = \int_{-\pi/2}^{\pi/2} \int_0^{2 \cos \theta} r^2\,dr\,d\theta = \int_{-\pi/2}^{\pi/2} \left[\dfrac{1}{3} r^3\right]_0^{2 \cos \theta}\,d\theta =$$

$$\dfrac{8}{3} \int_{-\pi/2}^{\pi/2} (\cos \theta)^3\,d\theta = \dfrac{8}{3} \left[\sin \theta - \dfrac{1}{3} (\sin \theta)^3\right]_{-\pi/2}^{\pi/2} = \dfrac{32}{9}.$$

Here's the work for the integral:

$$\int (\cos \theta)^3\,d\theta = \int (\cos \theta)^2 (\cos \theta)\,d\theta = \int \left(1 - (\sin \theta)^2\right) (\cos \theta)\,d\theta = \int (1 - u^2) \cos \theta \cdot \dfrac{du}{\cos \theta} = \int (1 - u^2)\,du =$$

$$\left[u = \sin \theta, \quad du = \cos \theta\,d\theta, \quad d\theta = \dfrac{du}{\cos \theta}\right]$$

$$u - \dfrac{1}{3} u^3 + c = \sin \theta - \dfrac{1}{3} (\sin \theta)^3 + c.\quad\halmos$$

7. Find the volume of the region which lies above the cone $z = \dfrac{1}{\sqrt{3}}\sqrt{x^2 + y^2}$ and below the hemisphere $z = \sqrt{1 - x^2 - y^2}$ .

$$\hbox{\epsfysize=1.75 in \epsffile{rev3-8.eps}}$$

I'll do the integral in spherical coordinates. It's pretty clear that the ranges for $\theta$ and $\rho$ are $0 \le \theta \le 2 \pi$ and $0 \le \rho \le 1$ . What is the range for $\phi$ ? I need to figure out the angle between the side of the cone and the z-axis.

To do this, take a random point on the cone: For instance, if $x = 1$ and $y = 0$ , then $z = \dfrac{1}{\sqrt{3}}$ . Here's the picture:

$$\hbox{\epsfysize=0.75 in \epsffile{rev3-9.eps}}$$

I drew a triangle with horizontal side 1 (since $r = \sqrt{x^2 + y^2} = \sqrt{1^2 + 0^2} = 1$ ) and vertical side $\dfrac{1}{\sqrt{3}}$ (the value of z). I found the hypotenuse using Pythagoras. Then I scaled the triangle up by multiplying all the sides by $\sqrt{3}$ so I could see the ratios better. In the second triangle, I can clearly see that the cone angle is $\dfrac{\pi}{3}$ .

Therefore, the range on $\phi$ is $0 \le \phi \le \dfrac{\pi}{3}$ .

The volume is

$$\tint_R\,dx\,dy\,dz = \int_0^{2 \pi} \int_0^{\pi/3} \int_0^1 \rho^2 \sin \phi\,d\rho\,d\phi\,d\theta = 2 \pi \int_0^{\pi/3} \sin \phi \left[\dfrac{1}{3} \rho^3\right]_0^1\,d\phi = \dfrac{2 \pi}{3} \int_0^{\pi/3} \sin \phi\,d\phi =$$

$$\dfrac{2 \pi}{3} \left[-\cos \phi\right]_0^{\pi/3} = \dfrac{\pi}{3} = 1.04719 \ldots.\quad\halmos$$

8. Compute $\displaystyle \int_0^1 \int_0^{\sqrt{1 - x^2}} \int_0^{x + y} \sqrt{x^2 + y^2}\,dz\,dy\,dx$ .

I'll convert to cylindrical coordinates. The ranges $0 \le x \le 1$ and $0 \le y \le \sqrt{1 - x^2}$ describe the interior of the circle of radius 1 centered at the origin which lies in the first quadrant:

$$\hbox{\epsfysize=1.75 in \epsffile{rev3-10.eps}}$$

In polar coordinates, it is

$$\left\{\matrix{ 0 \le \theta \le \dfrac{\pi}{2} \cr 0 \le r \le 1 \cr}\right\}$$

Note that

$$x + y = r \cos \theta + r \sin \theta.$$

Hence, the limits on z become $0 \le z \le r \cos \theta + r \sin \theta$ .

The integrand is $\sqrt{x^2 + y^2} = \sqrt{r^2} = r$ .

Therefore,

$$\int_0^1 \int_0^{\sqrt{1 - x^2}} \int_0^{x + y} \sqrt{x^2 + y^2}\,dz\,dy\,dx = \int_0^{\pi/2} \int_0^1 \int_0^{r \cos \theta + r \sin \theta} r^2\,dz\,dr\,d\theta =$$

$$\int_0^{\pi/2} \int_0^1 r^2 \left[z\right]_0^{r \cos \theta + r \sin \theta}\,dr\,d\theta = \int_0^{\pi/2} (\cos \theta + \sin \theta) \int_0^1 r^3\,dr\,d\theta = \int_0^{\pi/2} (\cos \theta + \sin \theta) \left[\dfrac{1}{4}r^4\right]_0^1\,d\theta =$$

$$\dfrac{1}{4} \int_0^{\pi/2} (\cos \theta + \sin \theta)\,d\theta = \dfrac{1}{4} \left[\sin \theta - \cos \theta\right]_0^{\pi/2} = \dfrac{1}{2}.\quad\halmos$$

9. Find the area of the part of the surface $z = 9 - x^2 - y^2$ which lies inside the cylinder $x^2 + y^2 = 1$ .

Since I'll be integrating over the region inside $x^2 + y^2 = 1$ , I'll do the double integral in polar. The region of integration is

$$\left\{\matrix{ 0 \le \theta \le 2 \pi \cr 0 \le r \le 1 \cr}\right\}.$$

The normal vector is

$$\vec{N} = \left(-\pder z x, -\pder z y, 1\right) = (2 x, 2 y, 1).$$

Hence,

$$\|vec{N}\| = \sqrt{4 x^2 + 4 y^2 + 1} = \sqrt{4 r^2 + 1}.$$

The area is

$$\int_0^{2 \pi} \int_0^1 \sqrt{4 r^2 + 1} \cdot r\,dr\,d\theta = 2 \pi \int_0^1 r \sqrt{4 r^2 + 1}\,dr = 2 \pi \int_1^5 r \sqrt{u} \cdot \dfrac{du}{8 r} = \dfrac{\pi}{4} \int_1^5 \sqrt{u}\,du =$$

$$\left[u = 4 r^2 + 1, \quad du = 8 r\,dr, \quad dr = \dfrac{du}{8 r}; \quad r = 0, u = 1; r = 1, u = 5\right]$$

$$\dfrac{\pi}{4} \left[\dfrac{2}{3} u^{3/2}\right]_1^5 = \dfrac{\pi}{6} (5^{3/2} - 1) = 5.33041 \ldots.\quad\halmos$$

10. Find the area of the surface

$$x = 2 u \cos v, \quad y = u^2, \quad z = 2 u \sin v, \quad 0 \le u \le 1, \quad 0 \le v \le 2 \pi.$$

$$\vec{T}_u = (2 \cos v, 2 u, 2 \sin v), \quad \vec{T}_v = (-2 u \sin v, 0, 2 u \cos v),$$

$$\vec{T}_u \times \vec{T}_v = \left|\matrix{ \ihat & \jhat & \khat \cr 2 \cos v & 2 u & 2 \sin v \cr -2 u \sin v & 0 & 2 u \cos v \cr}\right| = (4 u^2 \cos v, -4 u (\sin v)^2 - 4 u (\cos v)^2, 4 u^2 \sin v) =$$

$$(4 u^2 \cos v, -4 u, 4 u^2 \sin v),$$

$$\|\vec{T}_u \times \vec{T}_v\| = \sqrt{16 u^4 (\cos v)^2 + 16 u^2 + 16 u^4 (\sin v)^2} = \sqrt{16 u^4 + 16 u^2} = 4 u \sqrt{u^2 + 1}.$$

The area is

$$\int_0^{2 \pi} \int_0^1 4 u \sqrt{u^2 + 1}\,du\,dv = 8 \pi \int_0^1 u \sqrt{u^2 + 1}\,du = 8 \pi \left[\dfrac{1}{3} (u^2 + 1)^{3/2}\right]_0^1 = \dfrac{8 \pi}{3} (2^{3/2} - 1) = 15.31779 \ldots.$$

Here's the work for the integral:

$$\int u \sqrt{u^2 + 1}\,du = \int u \sqrt{w} \cdot \dfrac{dw}{2 u} = \dfrac{1}{2} \int \sqrt{w}\,dw = \dfrac{1}{3} w^{3/2} + c = \dfrac{1}{3} (u^2 + 1)^{3/2} + c.$$

$$\left[w = u^2 + 1, \quad dw = 2 u\,du, \quad du = \dfrac{dw}{2 u}\right]\quad\halmos$$

11. A lamina occupies the region in the x-y-plane bounded above by $y = 1$ and below by $y = x^2$ . The density is $\delta(x, y) = y + 1$ . Find the coordinates of the center of mass.

$$\hbox{\epsfysize=1.5 in \epsffile{rev3-12.eps}}$$

The region is given by

$$\left\{\matrix{ -1 \le x \le 1 \cr x^2 \le y \le 1 \cr}\right\}.$$

The mass is

$$\int_{-1}^1 \int_{x^2}^1 (y + 1)\,dy\,dx = \dfrac{32}{15}.$$

Note that the region is symmetric about the y-axis, and that the density is symmetric about the y-axis (since $\delta(x, y) = y + 1$ does not involve x). By symmetry, it follows that the center of mass must lie on the y-axis, i.e. that $\overline{x} = 0$ . Therefore, I only need to find $\overline{y}$ .

The moment in the y-direction is

$$m_y = \int_{-1}^1 \int_{x^2}^1 y(y + 1)\,dy\,dx = \dfrac{48}{35}.$$

Hence,

$$\overline{y} = \dfrac{\dfrac{48}{35}}{\dfrac{32}{15}} = \dfrac{9}{14}.\quad\halmos$$

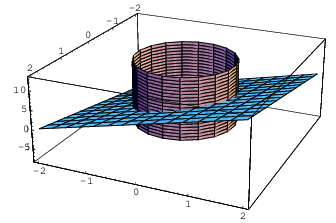
12. Let R be the region between $z = 2 x^2 + 2 y^2$ and $z = x^2 + y^2 + 4$ . Find the centroid of R.

R is the region between two paraboloids, both opening upward. (Think of the space between two bowls, one stacked on top of the other.) In the picture below, I've cut a chunk out of the surfaces so you can see the inner one inside the outer one.

$$\hbox{\epsfysize=1.75in \epsffile{rev3-15.eps}}$$

The region is symmetric about the z-axis, so $\overline{x} = \overline{y} = 0$ . Thus, I just need to find $\overline{z}$ .

I'll convert to cylindrical coordinates. Note that

$$z = 2 x^2 + 2 y^2 = 2 r^2 \quad\hbox{and}\quad z = x^2 + y^2 + 4 = r^2 + 4.$$

To find where the surfaces intersect, I solve the equations simultaneously:

$$\eqalign{ 2 r^2 & = r^2 + 4 \cr r^2 & = 4 \cr r & = 2 \cr}$$

So the region projects onto the interior of the circle of radius 2 centered at the origin in the x-y-plane.

$z = 2 r^2$ is the bottom of the region and $z = r^2 + 4$ is the top. The region is

$$\left\{\matrix{ 0 \le \theta \le 2 \pi \cr 0 \le r \le 2 \cr 2 r^2 \le z \le r^2 + 4 \cr}\right\}$$

The volume is

$$\int_0^{2 \pi} \int_0^2 (r^2 + 4 - 2 r^2) r\,dr\,d\theta = 2 \pi \int_0^2 (4 r - r^3)\,dr = 2 \pi \left[2 r^2 - \dfrac{1}{4} r^4\right]_0^2 = 8 \pi.$$

The z-moment is

$$\int_0^{2 \pi} \int_0^2 \int_{2 r^2}^{r^2 + 4} z \cdot r\,dz\,dr\,d\theta = 2 \pi \int_0^2 r \left[\dfrac{1}{2} z^2\right]_{2 r^2}^{r^2 + 4}\,dr = \pi \int_0^2 r [(r^2 + 4)^2 - (2 r^2)^2]\,dr =$$

$$\pi \int_0^2 (-3 r^5 + 8 r^3 + 16 r)\,dr \pi \left[-\dfrac{1}{6} r^6 + 2 r^4 + 8 r^2\right]_0^2 = 32 \pi.$$

Hence,

$$\overline{z} = \dfrac{32 \pi}{8 \pi} = 4.$$

The centroid is $(0, 0, 4)$ .

13. Compute $\displaystyle \dint_R (x - 2 y)\,dx\,dy$ , where R is the parallelogram with vertices $A(0, 1)$ , $B(2, 0)$ , $C(4, 2)$ , $D(2, 3)$ (counterclockwise).

$$\hbox{\epsfysize=2 in \epsffile{rev3-13.eps}}$$

I'll find a transformation which carries the unit square

$$\left\{\matrix{ 0 \le u \le 1 \cr 0 \le v \le 1 \cr}\right\} \quad\hbox{onto}\quad R.$$

$\bvec{A B} = (2, -1)$ and $\bvec{A D} = (2, 2)$ . The transformation is

$$\left[\matrix{x \cr y \cr}\right] = \left[\matrix{2 & 2 \cr -1 & 2 \cr}\right] \left[\matrix{u \cr v \cr}\right] + \left[\matrix{0 \cr 1 \cr}\right].$$

If I multiply out and combine terms on the right, then equate corresponding components, I get

$$x = 2 u + 2 v, \quad y = -u + 2 v + 1.$$

The Jacobian is

$$\det \left[\matrix{2 & -1 \cr 2 & 2 \cr}\right] = 6.$$

The integrand is

$$x - 2 y = (2 u + 2 v) - 2 (-u + 2 v + 1) = 4 u - 2 v - 2.$$

Hence,

$$\dint_R (x - 2 y)\,dx\,dy = \int_0^1 \int_0^1 (4 u - 2 v - 2)(6)\,du\,dv = 6 \int_0^1 \left[2 u^2 - 2 u v - 2 u\right]_0^1\,dv = 6 \int_0^1 (-2 v)\,dv =$$

$$-12 \left[\dfrac{1}{2} v^2\right]_0^1 = -6.\quad\halmos$$

14. (a) Let R be the region in the first quadrant bounded above by $y = 2 - x^2$ and bounded below by $y = 1 - x^2$ , from $x = 0$ to $x = 1$ . Find a transformation which carries the square

$$\left\{\matrix{ 0 \le u \le 1 \cr 0 \le v \le 1 \cr}\right\} \quad\hbox{onto}\quad R.$$

(b) Use a change of variables to evaluate

$$\dint_R (4 x^2 + y)\,dx\,dy.$$

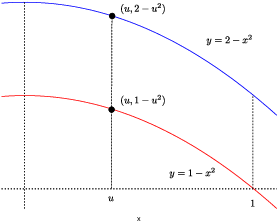
$$\hbox{\epsfysize=2in \epsffile{rev3-18.eps}}$$

(a) I'll parametrize the region by vertical segments. Consider the segment with x-coordinate u. The corresponding points are $(u, 1 - u^2)$ on $y = 1 - x^2$ and $(u, 2 - u^2)$ on $y = 2 - x^2$ . The segment from the first point to the second is

$$(x, y) = (1 - v) \cdot (u, 1 - u^2) + v \cdot (u, 2 - u^2) = (u, 1 - u^2 + v).$$

So

$$x = u, \quad y = 1 - u^2 + v.\quad\halmos$$

(b) The Jacobian is

$$\det \left[\matrix{1 & 0 \cr -2 u & 1 \cr}\right] = 1.$$

The function is

$$4 x^2 + y = 4 u^2 + 1 - u^2 + v = 3 u^2 + v + 1.$$

Hence,

$$\dint_R (4 x^2 + y)\,dx\,dy = \int_0^1 \int_0^1 (3 u^2 + v + 1)\,du\,dv = \int_0^1 \left[u^3 + u v + u\right]_0^1\,dv =$$

$$\int_0^1 (v + 2)\,dv = \left[\dfrac{1}{2} v^2 + 2 v\right]_0^1 = \dfrac{5}{2}.\quad\halmos$$

15. Let $f(x, y, z) = 3 x + y$ , and let

$$\vec{\sigma}(t) = \left(\dfrac{1}{3} t^3 + 1, 8 t - 3, 2 t^2\right), \quad 0 \le t \le 1.$$

Compute $\displaystyle \int_{\vec{\sigma}} f\,ds$ .

To compute the path integral, I need the length of the velocity vector:

$$\vec{\sigma}\,'(t) = \left(t^2, 8, 4 t\right).$$

$$\|\vec{\sigma}\,'(t)\| = \sqrt{(t^2)^2 + 8^2 + (4 t)^2} = \sqrt{t^4 + 16 t^2 + 64} = \sqrt{(t^2 + 8)^2} = t^2 + 8.$$

Next,

$$f(t) = 3 \left(\dfrac{1}{3} t^3 + 1\right) + (8 t - 3) = t^3 + 8 t.$$

The integral is

$$\int_{\vec{\sigma}} f\,ds = \int_0^1 (t^3 + 8 t)(t^2 + 8)\,dt = \int_0^1 \left(t^5 + 16 t^3 + 64 t\right)\,dt =$$

$$\left[\dfrac{1}{6} t^6 + 4 t^4 + 32 t^2\right]_0^1 = \dfrac{217}{6} = 36.16666 \ldots.\quad\halmos$$

16. Compute $\displaystyle \int_{\vec{\sigma}} (x + y)\,dx - (x - y)\,dy$ , where $\sigma$ is the path consisting of the segment from $(0, 1)$ to $(-1, 0)$ , the segment from $(-1, 0)$ to $(0, -1)$ , the segment from $(0, -1)$ to $(1, 0)$ , and the segment from $(1, 0)$ to $(0, 1)$ .

$$\hbox{\epsfysize=2 in \epsffile{rev3-11.eps}}$$

I'll break the integral up into four segments, as shown in the picture.

Segment A is $y = x + 1$ . For this segment, x goes from 0 to -1,

$$x + y = 2 x + 1, \quad x - y = -1, \quad dy = dx.$$

The integral is

$$\int_0^{-1} \left((2 x + 1)\,dx - (-1)\,dx\right) = \int_0^{-1} (2 x + 2)\,dx = \left[x^2 + 2 x\right]_0^{-1} = -1.$$

Segment B is $y = -x - 1$ . For this segment, x goes from -1 to 0,

$$x + y = -1, \quad x - y = 2 x + 1, \quad dy = -dx.$$

The integral is

$$\int_{-1}^0 \left(-dx - (2 x + 1)\,dx\right) = \int_{-1}^0 (-2 x - 2)\,dx = \left[-x^2 - 2 x\right]_{-1}^0 = -1.$$

Segment C is $y = x - 1$ . For this segment, x goes from 0 to 1,

$$x + y = 2 x - 1, \quad x - y = 1, \quad dy = dx.$$

The integral is

$$\int_0^1 \left((2 x - 1)\,dx - dx\right) = \int_0^1 (2 x - 2)\,dx = \left[x^2 - 2 x\right]_0^1 = -1.$$

Segment D is $y = 1 - x$ . For this segment, x goes from 1 to 0,

$$x + y = 1, \quad x - y = 2 x - 1, \quad dy = -dx.$$

The integral is

$$\int_1^0 \left(dx - (2 x - 1)dx\right) = \int_1^0 (2 - 2 x)\,dx = \left[2 x - x^2 \right]_1^0 = -1.$$

Therefore,

$$\int_{\vec{\sigma}} (x + y)\,dx - (x - y)\,dy = -1 + (-1) + (-1) + (-1) = -4.\quad\halmos$$

17. Compute $\displaystyle \int_{\vec{\sigma}} \vec{F} \cdot \bvec{ds}$ , where $\vec{\sigma}$ is the curve of intersection of $x^2 + y^2 = 1$ and the plane $z = 2 + 2 x + 3 y$ , traversed counterclockwise as viewed from above, and $\vec{F} = (-2 y, 2 x, 2)$ .

$$\hbox{\epsfysize=2 in \epsffile{rev3-14.eps}}$$

The projection of the curve into the x-y plane is the circle $x^2 + y^2 = 1$ , which may be parametrized by $x = \cos t$ , $y = \sin t$ for $0 \le t \le 2 \pi$ . Note that this parameter range traverses the circle counterclockwise as viewed from above.

Plugging these expressions into $z = 2 + 2 x + 3 y$ , I get $z = 2 + 2 \cos t + 3 \sin t$ . Hence, the curve of intersection is

$$\vec{\sigma}(t) = (\cos t, \sin t, 2 + 2 \cos t + 3 \sin t).$$

Therefore,

$$\vec{\sigma}\,'(t) = (-\sin t, \cos t, -2 \sin t + 3\cos t).$$

The integrand is

$$\vec{F}(\vec{\sigma}(t)) \cdot \vec{\sigma}\,'(t) = (-2 \sin t, 2 \cos t, 2) \cdot (-\sin t, \cos t, -2 \sin t + 3\cos t) =$$

$$2 (\sin t)^2 + 2 (\cos t)^2 - 4 \sin t + 6\cos t = 2 - 4 \sin t + 6 \cos t.$$

The integral is

$$\int_{\vec{\sigma}} \vec{F} \cdot \bvec{ds} = \int_0^{2 \pi} \left(2 - 4 \sin t + 6 \cos t\right)\,dt = \left[2 t + 4 \cos t + 6 \sin t\right]_0^{2 \pi} = 4 \pi = 12.56637 \ldots.\quad\halmos$$

18. Let $\vec{F}(x, y, z) = (x^2 y + z, x z, x + 3 y z)$ . Compute $\curl \vec{F}$ and $\diverg \vec{F}$ .

$$\curl \vec{F} = \left|\matrix{ \ihat & \jhat & \khat \cr \pder {} x & \pder {} y & \der {} z \cr x^2 y + z & x z & x + 3 y z \cr}\right| = (3 z - x, 1 - 1, z - x^2) = (3 z - x, 0, z - x^2).$$

$$\diverg \vec{F} = 2 x y + 0 + 3 y = 2 x y + 3 y.\quad\halmos$$

19. Let $\vec{\sigma}(t)$ be the path which consists of the curve $\left(\dfrac{3 t}{2 t + 1}, t e^{2 (t - 1)}, \dfrac{1}{8} t^2 (t^2 + 1)^3\right)$ for $ 0 \le t \le 1$ , followed by the segment from $(1, 1, 1)$ to $(1, 2, -1)$ .

Compute

$$\int_{\vec{\sigma}} (y^2 + z^3)\,dx + (2 x y - 2 y)\,dy + (3 x z^2 + 4)\,dz,$$

It would be very tedious to compute the line integral directly, and it should lead you to ask yourself whether there might not be an easier way. Well,

$$\curl (y^2 + z^3, 2 x y - 2 y, 3 x z^2 + 4) = \left|\matrix{ \ihat & \jhat & \khat \cr \pder {} x & \pder {} y & \pder {} z \cr y^2 + z^3 & 2 x y - 2 y & 3 x z^2 + 4 \cr}\right| = (0, 3 z^2 - 3 z^2, 2 y - 2 y) = (0, 0, 0).$$

The field is conservative. I'll find a potential function f. I want

$$\pder f x = y^2 + z^3, \quad \pder f y = 2 x y - 2 y, \quad \pder f z = 3 x z^2 + 4.$$

Integrate the first equation with respect to x:

$$f(x, y, z) = \int (y^2 + z^3)\,dx = x y^2 + x z^3 + C(y, z).$$

$C(y, z)$ is an arbitrary constant depending on y and z. Differentiate with respect to y and set the result equal to $\pder f y = 2 x y - 2 y$ :

$$2 x y + \pder C y = \pder f y = 2 x y - 2 y.$$

Cancelling $2 x y$ 's, I get $\pder C y = -2 y$ , so

$$C = \int -2 y\,dy = -y^2 + D(z).$$

$D(z)$ is an arbitrary constant depending on z. Then

$$f(x, y, z) = x y^2 + x z^3 - y^2 + D(z).$$

Differentiate with respect to z and set the result equal to $\pder f z = 3 x z^2 + 4$ :

$$3 x z^2 + D'(z) = \pder f z = 3 x z^2 + 4.$$

Cancelling $3 x z^2$ 's, I get $D'(z) = 4$ , so $D(z) = 4 z + E$ . Now E is a numerical arbitrary constant, and since I need some potential function, I can take $E = 0$ . Then

$$f(x, y, z) = x y^2 + x z^3 - y^2 + 4 z.$$

Now $\vec{\sigma}$ starts at $(0, 0, 0)$ (as you see by plugging $t = 0$ into $\left(\dfrac{3 t}{2 t + 1}, t e^{2 (t - 1)}, \dfrac{1}{8} t^2 (t^2 + 1)^3\right)$ ), and it ends at $(1, 2, -1)$ . By path independence,

$$\int_{\vec{\sigma}} (y^2 + z^3)\,dx + (2 x y - 2 y)\,dy + (3 x z^2 + 4)\,dz = f(1, 2, -1) - f(0, 0, 0) = -5.\quad\halmos$$

20. Let $\vec{\sigma}$ be the boundary of the square $0 \le x \le 1$ , $0 \le y \le 1$ , traversed in the counterclockwise direction.

Compute

$$\int_{\vec{\sigma}} (x^2 y - x y^2)\,dx + \left(2 x^2 y + \dfrac{1}{3} x^3\right)\,dy.$$

$$\hbox{\epsfysize=1.75in \epsffile{rev3-17.eps}}$$

I'll use Green's Theorem.

The region is

$$\left\{\matrix{ 0 \le x \le 1 \cr 0 \le y \le 1 \cr}\right\}$$

$$\pder Q x - \pder P y = (4 x y + x^2) - (x^2 - 2 x y) = 6 x y.$$

Hence,

$$\int_{\vec{\sigma}} (x^2 y - x y^2)\,dx + \left(2 x^2 y + \dfrac{1}{3} x^3\right)\,dy = \int_0^1 \int_0^1 6 x y\,dx\,dy = \int_0^1 \left[3 x^2 y\right]_0^1\,dy =$$

$$\int_0^1 3 y\,dy = \left[\dfrac{3}{2} y^2 \right]_0^1 = \dfrac{3}{2}.\quad\halmos$$

21. Let $\vec{\sigma}$ be the boundary of the region bounded below by $y = x^2$ and above by $y = 4$ , traversed counterclockwise. Compute

$$\int_{\vec{\sigma}} (4 x y - 2 y^2)\,dx + (2 x^2 + y^4)\,dy.$$

$$\hbox{\epsfysize=1.75in \epsffile{rev3-16.eps}}$$

I'll use Green's theorem. The region is

$$\left\{\matrix{ -2 \le x \le 2 \cr x^2 \le y \le 4 \cr}\right\}$$

$$\pder Q x - \pder P y = 4 x - (4 x - 4 y) = 4 y.$$

Hence,

$$\int_{\vec{\sigma}} (4 x y - 2 y^2)\,dx + (2 x^2 + y^4)\,dy = \int_{-2}^2 \int_{x^2}^4 4 y\,dy\,dx = \int_{-2}^2 \left[2 y^2\right]_{x^2}^4\,dx = 2 \int_{-2}^2 \left(16 - x^4\right)\,dx =$$

$$2 \left[16 x - \dfrac{1}{5} x^5\right]_{-2}^2 = \dfrac{512}{5} = 102.4.\quad\halmos$$

22. Find the area of the region enclosed by the ellipse

$$\dfrac{x^2}{4} + \dfrac{y^2}{9} = 1.$$

Parametrize the ellipse by

$$\vec{\sigma}(t) = (2 \cos t, 3 \sin t), \quad 0 \le t \le 2 \pi.$$

This curve traverses the ellipse counterclockwise. By Green's Theorem, the area is

$$\int_{\vec{\sigma}} x\,dy = \int_0^{2 \pi} x \cdot \der y t\,dt = \int_0^{2 \pi} (2 \cos t)(3 \cos t)\,dy = 6 \int_0^{2 \pi} (\cos t)^2 \,dt = 3 \int_0^{2 \pi} (1 + \cos 2 t)\,dt =$$

$$3 \left[t + \dfrac{1}{2} \sin 2 t\right]_0^{2 \pi} = 6 \pi.\quad\halmos$$

There's a difference between forgetting and not recalling. - Alessandro Morandotti

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga