Review Sheet for Test 2

Math 310

These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the absence of a topic does not imply that it won't appear on the test.

1. Premises: $\left\{\matrix{(\lnot P \lor Q) \ifthen (R \land \lnot S) \cr \lnot S \ifthen \lnot R \cr}\right.$

Prove: P.

2. Premises: $\left\{\matrix{(\lnot C \lor \lnot D) \ifthen B \cr B \ifthen A \cr \lnot A \lor C \cr}\right.$

Prove: C.

3. Premises: $\left\{\matrix{(\lnot P \lor S) \ifthen R \cr Q \ifthen \lnot P \cr Q \lor R \cr}\right.$

Prove: R.

4. Let x and y be positive real numbers. Prove that if $\dfrac{1}{x} + \dfrac{1}{y} = 2$ , then either $x \ge 1$ or $y \ge 1$ .

5. Prove that the following inequality has no real solutions:

$$x^2 y^2 + 6 + x^2 - 4 xy + y^2 < 0.$$

6. Rolle's theorem says that if f is a continuous function on the interval $a \le x \le b$ , f is differentiable on the interval $a < x < b$ , and $f(a) = f(b)$ , then $f'(c) = 0$ for some number c such that $a < c < b$ .

Use Rolle's theorem to prove that if $k > 0$ , then $f(x) = x^5 + x^3 + kx + 1$ does not have more than one root.

7. Prove that if an integer is squared and divided by 3, the remainder can't be 2. [Hint: Take cases. If the given integer is divided by 3, it leaves a remainder of 0, 1, or 2.]

8. Prove that if n is an integer, then $n^2 + 2 n + 2$ is not divisible by 3.

9. Prove that if $x \in \real$ , then

$$-4 \le |x - 2| - |x - 6| \le 4.$$

10. Prove that for all $x \in \real$ , $|x + 1| + |2 x - 6| \ge 4$ .

11. Prove that if $n \in \integer$ and $n \ge 1$ , then $x^n - y^n$ is divisible by $x - y$ . Note: This means that there's a polynomial $p(x, y)$ in x and y with integer coefficients such that $(x - y) \cdot p(x, y) = x^n - y^n$ .

12. Prove that $\displaystyle \sum_{k=1}^n (-1)^{k+1} k^2 = (-1)^{n+1} \dfrac{n(n + 1)}{2}$ for all $n \ge 1$ .

13. Prove that if $n \in \natural$ , then

$$\sum_{k=1}^n (k^2 + k + 1)k! = (n + 1)(n + 1)! - 1.$$

14. A sequence of integers is defined by

$$x_0 = 7, \quad x_1 = -10,$$

$$x_n = -4 x_{n-1} + 12 x_{n-2} \quad\hbox{for}\quad n \ge 2.$$

Prove that for all $n \ge 0$ ,

$$x_n = 3 \cdot (-6)^n + 4 \cdot 2^n.$$

15. Prove that if $n \ge 2$ , then

$$5^n > 2^n + 3^n.$$

16. (a) What would be a counterexample to the statement "Every dog likes cheese"?

(b) Give a counterexample to the following statement: "For all integers a, b, and c, if a divides $b c$ , then a divides b or a divides c."

17. Give a specific counterexample which shows that the following equations are not algebraic identities.

(a) "$2(x y) = (2 x)(2 y)$ ".

(b) "$\sin (x + y) = \sin x + \sin y$ ".

18. Give counterexamples to the following statements:

(a) "If $x, y \in \real$ and $x \le y$ , then $\sin x \le \sin y$ ."

(b) "If $a, b, c, d \in \real$ and $a \le b$ and $c \le d$ , then $a c \le b d$ ."

19. Give a counterexample to the following statement: "If $x^2 - 4 x + 3 = 0$ , then $x = 1$ ."

20. Suppose the universe is $U = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}$ , and:

$A = \{1, 2, 3, 4, 5\}$ ,

$B = \{2, 4, 6, 8, 10\}$ ,

$C = \{1, 3, 5, 7, 9\}$ .

(a) List the elements of $\complement{A}$ .

(b) List the elements of $A \cap C$ .

(c) List the elements of $A \cup B$ .

(d) List the elements of $(A \cup C) - B$ .

21. Construct Venn diagrams for the following sets:

(a) $A - (B - C)$

(b) $A \cap (B \cup C)$

22. What sets are represented by the shaded regions in the following Venn diagrams?

$$\matrix{\hbox{\epsfysize=1.75in \epsffile{rev2-8a.eps}} & \hbox{\epsfysize=1.75in \epsffile{rev2-8b.eps}} \cr {\rm (a)} & {\rm (b)} \cr}$$

23. (a) List the elements of the set $\{a, \{b,c\}\}$ .

(b) List the elements of the set $\{\{d\}\}$ .

(c) Is $\{a,b\}$ a subset of $\{a, \{b,c\}\}$ ? Why or why not?

24. (a) Suppose $A = \{1, a, \emptyset\}$ . List the elements of $\powerset(A)$ .

(b) How many subsets does the set $\{n \in \natural \mid 2 \le n \le 10\}$ have?

25. (a) Suppose $X = \{a, b\}$ and $Y = \{1, 2, 42\}$ . List the elements of $X \times Y$ .

(b) Are the sets $\{1, 2\}$ and $\{2, 1\}$ equal? Are the ordered pairs $(1, 2)$ and $(2, 1)$ equal?

(c) Suppose $|X| = 5$ and $|Y| = 4$ . Find $|X \times Y|$ and $|\powerset(X \times Y)|$ .

26. Let A, B, and C be sets. Prove that

$$A \cap B \subset (A \cup C) \cap (B \cup C).$$

27. Let A, B, and C be sets. Prove that

$$(C - A) \cup B = (A \cap B) \cup \left[(C \cup B) - A\right].$$

28. Let A and B be sets. Prove that

$$(A - B) \cap (B - A) = \emptyset.$$

29. Let A and B be sets.

(a) Prove that $A \subset A \cup B$ and $B \subset A \cup B$ .

(b) Prove that $A \cup B = B$ if and only if $A \subset B$ .

30. Recall that

$$(a, b) = \{x \in \real \mid x > a \land x < b\}.$$

Prove that $(1, 3) \cap (2, 4) = (2, 3)$ .

31. Recall that

$$[a, b] = \{x \in \real \mid x \ge a \land x \le b\}.$$

Prove that $[-2, 3] \cup [1, 5] = [-2, 5]$ .

32. Suppose $S = \{1, 2\}$ and $T = \{a, b\}$ . List the elements of $S \times T$ and $T \times S$ .

33. Give a specific example of two sets A and B for which $A \times B \ne B \times A$ .

34. Prove using the limit definition that

$$\lim_{n \to \infty} \dfrac{3 n + 5}{n + 1} = 3.$$

35. Prove using the limit definition that

$$\lim_{n \to \infty} \dfrac{10 n}{2 n + 1} = 5.$$

Solutions to the Review Sheet for Test 2

1. Premises: $\left\{\matrix{(\lnot P \lor Q) \ifthen (R \land \lnot S) \cr \lnot S \ifthen \lnot R \cr}\right.$

Prove: P.

$$\matrix{ 1. \hfill & \lnot P \lor Q) \ifthen (R \land \lnot S) \hfill & \hbox{Premise} \hfill \cr 2. \hfill & \lnot S \ifthen \lnot R \hfill & \hbox{Premise} \hfill \cr 3. \hfill & \lnot P \hfill & \hbox{Premise for proof by contradiction} \hfill \cr 4. \hfill & \lnot P \lor Q \hfill & \hbox{Constructing a disjunction (3)} \hfill \cr 5. \hfill & R \land \lnot S \hfill & \hbox{Modus ponens (1,4)} \hfill \cr 6. \hfill & R \hfill & \hbox{Decomposing a conjunction (5)} \hfill \cr 7. \hfill & \lnot S \hfill & \hbox{Decomposing a conjunction (5)} \hfill \cr 8. \hfill & S \hfill & \hbox{Modus tollens (2,6)} \hfill \cr 9. \hfill & S \land \lnot S \hfill & \hbox{Constructing a conjunction (7,8)} \hfill \cr 10. \hfill & P \hfill & \hbox{Proof by contradiction (3,9)} \quad\halmos \hfill \cr}$$

2. Premises: $\left\{\matrix{(\lnot C \lor \lnot D) \ifthen B \cr B \ifthen A \cr \lnot A \lor C \cr}\right.$

Prove: C.

$$\matrix{ 1. \hfill & B \ifthen A \hfill & \hbox{Premise} \hfill \cr 2. \hfill & \lnot A \lor C \hfill & \hbox{Premise} \hfill \cr 3. \hfill & (\lnot C \lor \lnot D) \ifthen B \hfill & \hbox{Premise} \hfill \cr 4. \hfill & B \hfill & \hbox{Premise for proof by cases} \hfill \cr 5. \hfill & A \hfill & \hbox{Modus ponens (1, 4)} \hfill \cr 6. \hfill & C \hfill & \hbox{Disjunctive syllogism (2, 5)} \hfill \cr 7. \hfill & \lnot B \hfill & \hbox{Premise for proof by cases} \hfill \cr 8. \hfill & \lnot(\lnot C \lor \lnot D) \hfill & \hbox{Modus tollens (3, 7)} \hfill \cr 9. \hfill & C \land D \hfill & \hbox{DeMorgan's law (8)} \hfill \cr 10. \hfill & C \hfill & \hbox{Decomposing a conjunction (9)} \hfill \cr 11. \hfill & C \hfill & \hbox{Proof by cases (4, 6, 7, 10)} \quad\halmos \hfill \cr}$$

3. Premises: 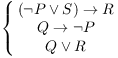$\left\{\matrix{(\lnot P \lor S) \ifthen R \cr Q \ifthen \lnot P \cr Q \lor R \cr}\right.$

Prove: R.

$$\matrix{ 1. \hfill & (\lnot P \lor S) \ifthen R \hfill & \hbox{Premise} \hfill \cr 2. \hfill & Q \ifthen \lnot P \hfill & \hbox{Premise} \hfill \cr 3. \hfill & Q \lor R \hfill & \hbox{Premise} \hfill \cr 4. \hfill & P \hfill & \hbox{Premise for proof by cases} \hfill \cr 5. \hfill & \lnot Q \hfill & \hbox{Modus tollens (2, 4)} \hfill \cr 6. \hfill & R \hfill & \hbox{Disjunctive syllogism (3, 5)} \hfill \cr 7. \hfill & \lnot P \hfill & \hbox{Premise for proof by cases} \hfill \cr 8. \hfill & \lnot P \lor S \hfill & \hbox{Constructing a disjunction (7)} \hfill \cr 9. \hfill & R \hfill & \hbox{Modus ponens (1, 8)} \hfill \cr 10. \hfill & R \hfill & \hbox{Proof by cases (4, 6, 7, 9)} \quad\halmos \hfill \cr}$$

4. Let x and y be positive real numbers. Prove that if $\dfrac{1}{x} + \dfrac{1}{y} = 2$ , then either $x \ge 1$ or $y \ge 1$ .

Suppose that x and y are positive real numbers, and $\dfrac{1}{x} + \dfrac{1}{y} = 2$ . I want to prove that either $x \ge 1$ or $y \ge 1$ .

I will give a proof by contradiction. The negation of "Either $x \ge 1$ or $y \ge 1$ " is "$x < 1$ and $y < 1$ ". So suppose on the contrary that $x < 1$ and $y < 1$ .

Since $x < 1$ and x is positive, $\dfrac{1}{x} > 1$ . Since $y < 1$ and y is positive, $\dfrac{1}{y} > 1$ . Therefore,

$$\dfrac{1}{x} + \dfrac{1}{y} > 1 + 1 = 2.$$

This contradicts my assumption that $\dfrac{1}{x} + \dfrac{1}{y} = 2$ . Therefore, either $x \ge 1$ or $y \ge 1$ .

5. Prove that the following inequality has no real solutions:

$$x^2 y^2 + 6 + x^2 - 4 xy + y^2 < 0.$$

I'll use proof by contradiction. Suppose that $(x,y)$ is a solution to the inequality. I'll rewrite the inequality using basic algebra, the idea being to try to complete the squares:

$$\eqalign{x^2 y^2 + 6 + x^2 - 4 xy + y^2 &< 0 \cr x^2 y^2 - 2 xy + 6 + x^2 - 2 xy + y^2 &< 0 \cr x^2 y^2 - 2 xy + 6 + (x - y)^2 &< 0 \cr x^2 y^2 - 2 xy + 1 + (x - y)^2 + 5 &< 0 \cr (xy - 1)^2 + (x - y)^2 + 5 &< 0 \cr}$$

The last inequality gives a contradiction: The two square terms must be greater than or equal to 0, so adding 5 makes the left side strictly positive. However, the inequality says that the left side is negative.

This contradiction shows that the original inequality has no solutions.

6. Rolle's theorem says that if f is a continuous function on the interval $a \le x \le b$ , f is differentiable on the interval $a < x < b$ , and $f(a) = f(b)$ , then $f'(c) = 0$ for some number c such that $a < c < b$ .

Use Rolle's theorem to prove that if $k > 0$ , then $f(x) = x^5 + x^3 + k x + 1$ does not have more than one root.

Suppose on the contrary that f has more than one root. Then f must have at least two different roots, say a and b. Thus, $f(a) = 0$ and $f(b) = 0$ . I'll assume that $a < b$ ; if it's the other way around, just switch their names.

Now f is a polynomial, so it's differentiable and continuous everywhere. In addition, $f(a) = 0 = f(b)$ . Therefore, Rolle's theorem applies, and I know that $f'(c) = 0$ for some c such that $a < c < b$ .

On the other hand,

$$f'(x) = 5 x^4 + 3 x^2 + k > 0 \quad\hbox{for all}\quad x.$$

Reason: The first two term are positive numbers multiplied by even powers of x, so they're both greater than or equal to 0. The last term k was given to be greater than 0.

Therefore, $f'(x)$ can't be equal to 0, which contradicts the existence of a number c where $f'(c) = 0$ .

Therefore, f does not have more than one root.

7. Prove that if an integer is squared and divided by 3, the remainder can't be 2.

Let n be an integer. I want to show that $n^2$ does not leave a remainder of 2 when it's divided by 3.

When n is divided by 3, it can leave a remainder of 0, 1, or 2. I consider cases.

If n leaves a remainder of 0 when it's divided by 3, then $n = 3k$ for some integer k. Hence,

$$n^2 = (3k)^2 = 9k^2 = 3(3k^2).$$

Therefore, $n^2$ leaves a remainder of 0 when it's divided by 3.

If n leaves a remainder of 1 when it's divided by 3, then $n = 3k + 1$ for some integer k. Hence,

$$n^2 = (3k + 1)^2 = 9k^2 + 6k + 1 = 3(3k^2 + 2k) + 1.$$

Therefore, $n^2$ leaves a remainder of 1 when it's divided by 3.

Finally, if n leaves a remainder of 2 when it's divided by 3, then $n = 3k + 2$ for some integer k. Hence,

$$n^2 = (3k + 2)^2 = 9k^2 + 12k + 4 = 9k^2 + 12k + 3 + 1 = 3(3k^2 + 4k + 1) + 1.$$

Therefore, $n^2$ leaves a remainder of 1 when it's divided by 3.

I've exhausted all the cases. Hence, if n is an integer, then $n^2$ does not leave a remainder of 2 when it's divided by 3.

Note: This kind of problem is much easier to do using modular arithmetic.

8. Prove that if n is an integer, then $n^2 + 2 n + 2$ is not divisible by 3.

Every integer n can be written in one of the forms $3q$ , $3q + 1$ , or $3q + 2$ , where q is an integer.

Case 1. If $n = 3q$ , then

$$n^2 + 2 n + 2 = 9q^2 + 6q + 2 = 3(3q^2 + 2q) + 2.$$

In this case, $n^2 + 2 n + 2$ leaves a remainder of 2 when it's divided by 3.

Case 2. If $n = 3q + 1$ , then

$$n^2 + 2 n + 2 = 9q^2 + 12q + 5 = 3(3q^2 + 4q + 1) + 2.$$

In this case, $n^2 + 2 n + 2$ leaves a remainder of 2 when it's divided by 3.

Case 3. If $n = 3q + 2$ , then

$$n^2 + 2 n + 2 = 9q^2 + 18q + 10 = 3(3q^2 + 6q + 3) + 1.$$

In this case, $n^2 + 2 n + 2$ leaves a remainder of 1 when it's divided by 3.

Therefore, if n is an integer, $n^2 + 2 n + 2$ is not divisible by 3.

9. Prove that if $x \in \real$ , then

$$-4 \le |x - 2| - |x - 6| \le 4.$$

Case 1. $x < 2$ .

In this case

$$|x - 2| = -(x - 2) = -x + 2 \quad\hbox{and}\quad |x - 6| = -(x - 6) = -x + 6.$$

So

$$|x - 2| - |x - 6| = (-x + 2) - (-x + 6) = -4.$$

Therefore, $-4 \le |x - 2| - |x - 6| \le 4$ .

Case 2. $2 \le x \le 6$ .

In this case

$$|x - 2| = x - 2 \quad\hbox{and}\quad |x - 6| = -(x - 6) = -x + 6.$$

So

$$|x - 2| - |x - 6| = (x - 2) - (-x + 6) = 2 x - 8.$$

Now

$$\eqalign{ 2 & \le x \le 6 \cr 4 & \le 2 x \le 12 \cr -4 & \le 2 x - 8 \le 4 \cr}$$

Therefore, $-4 \le |x - 2| - |x - 6| \le 4$ .

Case 3. $x > 6$ .

In this case

$$|x - 2| = x - 2 \quad\hbox{and}\quad |x - 6| = x - 6.$$

So

$$|x - 2| - |x - 6| = (x - 2) - (x - 6) = 4.$$

Therefore, $-4 \le |x - 2| - |x - 6| \le 4$ .

Since the result holds in all three cases, and the cases cover all $x \in \real$ , it follows that $-4 \le |x - 2| - |x - 6| \le 4$ for all $x \in \real$ .

10. Prove that for all $x \in \real$ , $|x + 1| + |2 x - 6| \ge 4$ .

(It is not a proof to draw the graph!)

I'll take cases to get rid of the absolute values.

$$|x + 1| = \cases{x + 1 & if $x \ge -1$ \cr -(x + 1) & if $x < -1$ \cr} \quad\hbox{and}\quad |2 x - 6| = \cases{2 x - 6 & if $x \ge 3$ \cr -(2 x - 6) & if $x < 3$ \cr}.$$

My cases will be $x < -1$ , $-1 \le x < 3$ , and $x \ge 3$ . This accounts for all $x \in \real$ .

Suppose that $x < -1$ . Then $|x + 1| = -(x + 1)$ , and since $x < -1 < 3$ , $|2 x - 6| = -(2 x - 6)$ . Therefore,

$$|x + 1| + |2 x - 6| = -(x + 1) - (2 x - 6) = 5 - 3 x.$$

Now

$$\eqalign{ x & < -1 \cr -3 x & > 3 \cr 5 - 3 x & > 8 > 4 \cr 5 - 3 x & \ge 4 \cr |x + 1| + |2 x - 6| & \ge 4 \cr}$$

Hence, the result is true for $x < -1$ .

Suppose that $-1 \le x < 3$ . Since $x \ge -1$ , $|x + 1| = x + 1$ . Since $x < 3$ , $|2 x - 6| = -(2 x - 6)$ . Therefore,

$$|x + 1| + |2 x - 6| = (x + 1) - (2 x - 6) = 7 - x.$$

Now

$$\eqalign{ -1 \le x & < 3 \cr 1 \ge -x & > -3 \cr 8 \ge 7 - x & > 4 \cr 7 - x & \ge 4 \cr |x + 1| + |2 x - 6| & \ge 4 \cr}$$

Hence, the result is true for $-1 \le x < 3$ .

Finally, suppose that $x \ge 3$ . This implies that $|2 x - 6| = 2 x - 6$ . Moreover, since $x \ge 3 > -1$ , $|x + 1| = x + 1$ . Therefore,

$$|x + 1| + |2 x - 6| = (x + 1) + (2 x - 6) = 3 x - 5.$$

Now

$$\eqalign{ x & \ge 3 \cr 3 x & \ge 9 \cr 3 x - 5 & \ge 4 \cr |x + 1| + |2 x - 6| & \ge 4 \cr}$$

Hence, the result is true for $x \ge 3$ .

Since in all three cases I have $|x + 1| + |2 x - 6| \ge 4$ , this is true for all $x \in \real$ .

11. Prove that if $n \in \integer$ and $n \ge 1$ , then $x^n - y^n$ is divisible by $x - y$ .

I'll use induction on n.

For $n = 1$ , $x^n - y^n = x - y$ , which is obviously divisible by $x - y$ . For $n = 2$ ,

$$x^n - y^n = x^ - y^2 = (x - y)(x + y).$$

This is also divisible by $x - y$ .

Let $n > 2$ , and assume the result is true for all powers less than n. In particular, assume that $x^{n-2} - y^{n-2}$ and $x^{n-1} - y^{n-1}$ are divisible by $x - y$ . I want to prove that $x^n - y^n$ is divisible by $x - y$ .

Since $x^{n-2} - y^{n-2}$ and $x^{n-1} - y^{n-1}$ are divisible by $x - y$ , there are polynomials $p(x, y)$ and $q(x, y)$ in the variables x and y such that

$$x^{n-2} - y^{n-2} = p(x, y)(x - y),$$

$$x^{n-1} - y^{n-1} = q(x, y)(x - y) \eqno{(*)}.$$

I'll use (*) to build the expression $x^n - y^n$ that I'm interested in. I'll make an $x^n$ first: Multiply (*) by x:

$$x^n - x y^{n-1} = x q(x, y)(x - y), \quad x^n = x y^{n-1} + x q(x, y)(x - y).$$

Next, make the $y^n$ : Multiply (*) by y:

$$x^{n-1} y - y^n = y q(x, y)(x - y), \quad -y^n = -x^{n-1} y + y q(x,y)(x - y).$$

Now add the expressions for $x^n$ and $-y^n$ and do some algebra, substituting eventually for $x^{n-2} - y^{n-2}$ :

$$x^n - y^n = x y^{n-1} - x^{n-1} y + x q(x, y)(x - y) + y q(x, y)(x - y) = x y(y^{n-2} - x^{n-2}) + (x + y)q(x, y)(x - y) =$$

$$-x y p(x, y)(x - y) + (x + y)q(x, y)(x - y).$$

Both terms on the right side are divisible by $x - y$ , so $x^n - y^n$ is divisible by $x - y$ . By induction, $x^n - y^n$ is divisible by $x - y$ for all $n \ge 1$ .

12. Prove that $\displaystyle \sum_{k=1}^n (-1)^{k+1} k^2 = (-1)^{n+1} \dfrac{n(n + 1)}{2}$ for all $n \ge 1$ .

I'll use induction on n. For $n = 1$ ,

$$\sum_{k=1}^n (-1)^{k+1} k^2 = (-1)^2 1^2 = 1, \quad\hbox{while}\quad \dfrac{n(n + 1)}{2} = \dfrac{1\cdot 2}{2} = 2.$$

Let $n > 1$ , and suppose the result is true for $n - 1$ . Thus, assume that

$$\sum_{k=1}^{n-1} (-1)^{k+1} k^2 = (-1)^{n} \dfrac{(n - 1)n}{2}.$$

I want to prove that result for n. Start with the summation for n, "peel off" the $n^{\rm th}$ term, and use the induction hypothesis:

$$\sum_{k=1}^n (-1)^{k+1} k^2 = \sum_{k=1}^{n-1} (-1)^{k+1} k^2 + (-1)^{n+1} n^2 = (-1)^{n} \dfrac{(n - 1)n}{2} + (-1)^{n+1} n^2 = (-1)^n\cdot n\cdot \left(\dfrac{n - 1}{2} - n\right) =$$

$$(-1)^n\cdot n\cdot \left(-\dfrac{1}{2} - \dfrac{n}{2}\right) = (-1)^n\cdot n\cdot \left(-\dfrac{n + 1}{2}\right) = (-1)^{n+1}\dfrac{n(n + 1)}{2}.$$

This proves the result for n, so the result is true for all $n \ge 1$ , by induction.

13. Prove that if $n \in \natural$ , then

$$\sum_{k=1}^n (k^2 + k + 1)k! = (n + 1)(n + 1)! - 1.$$

For $n = 1$ , I have

$$\sum_{k=1}^1 (k^2 + k + 1)k! = 3 \cdot 1! = 3 \quad\hbox{and}\quad (1 + 1)(1 + 1)! - 1 = 4 - 1 = 3.$$

Hence, the result is true for $n = 1$ .

Assume the result for n:

$$\sum_{k=1}^n (k^2 + k + 1)k! = (n + 1)(n + 1)! - 1.$$

I need to prove the result for $n + 1$ :

$$\sum_{k=1}^{n+1} (k^2 + k + 1)k! = (n + 2)(n + 2)! - 1.$$

I have

$$\eqalign{ \sum_{k=1}^{n+1} (k^2 + k + 1)k! & = \sum_{k=1}^n (k^2 + k + 1)k! + [(n + 1)^2 + (n + 1) + 1](n + 1)! \cr & = [(n + 1)(n + 1)! - 1] + [(n + 1)^2 + (n + 1) + 1](n + 1)! \cr & = [(n + 1)^2 + (n + 1) + 1 + (n + 1)](n + 1)! - 1 \cr & = [(n^2 + 2 n + 1) + (n + 1) + 1 + (n + 1)](n + 1)! - 1 \cr & = (n^2 + 4 n + 4)(n + 1)! - 1 \cr & = (n + 2)(n + 2)(n + 1)! - 1 \cr & = (n + 2)(n + 2)! - 1 \cr}$$

This proves the result for $n + 1$ , so the result is true for all $n \in \natural$ , by induction.

14. A sequence of integers is defined by

$$x_0 = 7, \quad x_1 = -10,$$

$$x_n = -4 x_{n-1} + 12 x_{n-2} \quad\hbox{for}\quad n \ge 2.$$

Prove that for all $n \ge 0$ ,

$$x_n = 3 \cdot (-6)^n + 4 \cdot 2^n.$$

For $n = 0$ , the formula gives

$$x_0 = 3 \cdot (-6)^0 + 4 \cdot 2^0 = 3 + 4 = 7.$$

For $n = 1$ , the formula gives

$$x_1 = 3 \cdot (-6)^1 + 4 \cdot 2^1 = -10.$$

Therefore, the result is true for $n = 0$ and $n = 1$ .

Assume $n \ge 2$ , and suppose the result holds for $k < n$ . Then

$$x_n = -4 x_{n-1} + 12 x_{n-2} = -4 \left(3 \cdot (-6)^{n - 1} + 4 \cdot 2^{n - 1}\right) + 12 \cdot \left(3 \cdot (-6)^{n - 2} + 4 \cdot 2^{n - 2}\right) =$$

$$\left(-12 \cdot (-6)^{n - 1} + 36 \cdot (-6)^{n - 2}\right) + \left((-16) \cdot 2^{n - 1} + 48 \cdot 2^{n - 2}\right) =$$

$$3 \cdot (-6)^{n - 2} \left(-4 \cdot (-6) + 12\right) + 4 \cdot 2^{n - 2} \left(-4 \cdot 2 + 12\right) =$$

$$3 \cdot (-6)^{n - 2} \cdot 36 + 4 \cdot 2^{n - 2} \cdot 4 = 3 \cdot (-6)^{n - 2} \cdot (-6)^2 + 4 \cdot 2^{n - 2} \cdot 2^2 = 3 \cdot (-6)^n + 4 \cdot 2^n.$$

This proves the result for n, so the result holds for all $n \ge 0$ by induction.

15. Prove that if $n \ge 2$ , then

$$5^n > 2^n + 3^n.$$

For $n = 2$ ,

$$5^n = 5^2 = 25,$$

$$2^n + 3^n = 2^2 + 3^2 = 13.$$

Thus, $5^2 > 2^2 + 3^2$ , and the result is true for $n = 2$ .

Assume that the result is true for n:

$$5^n > 2^n + 3^n.$$

I'll prove the result for $n + 1$ :

$$\eqalign{ 5^{n + 1} & = 5 \cdot 5^n \cr & > 5(2^n + 3^n) \cr & = 5 \cdot 2^n + 5 \cdot 3^n \cr & > 2 \cdot 2^n + 3 \cdot 3^n \cr & = 2^{n+1} + 3^{n+1} \cr}$$

This proves the result for $n + 1$ , so the result is true for all $n \ge 2$ by induction.

16. (a) What would be a counterexample to the statement "Every dog likes cheese"?

(b) Give a counterexample to the following statement: "For all integers a, b, and c, if a divides $b c$ , then a divides b or a divides c."

(a) A counterexample would be a dog who does not like cheese.

(b) Let $a = 12$ , $b = 6$ , and $c = 4$ . Then 12 divides $6\cdot 4 = 24$ , but 12 does not divide 6 and 12 does not divide 4.

17. Give a specific counterexample which shows that the following equations are not algebraic identities.

(a) "$2(x y) = (2 x)(2 y)$ ".

(b) "$\sin (x + y) = \sin x + \sin y$ ".

(a) If $x = 1$ and $y = 3$ , then

$$2(x y) = 2(1 \cdot 3) = 2 \cdot 3 = 6, \quad\hbox{but}\quad (2 x)(2 y) = (2 \cdot 1)(2 \cdot 3) = (2)(6) = 12.\quad\halmos$$

(b) If $x = \dfrac{\pi}{2}$ and $y = \dfrac{\pi}{2}$ , then

$$\sin (x + y) = \sin \left(\dfrac{\pi}{2} + \dfrac{\pi}{2}\right) = \sin \pi = 0, \quad\hbox{but}\quad \sin x + \sin y = \sin \dfrac{\pi}{2} + \sin \dfrac{\pi}{2} = 1 + 1 = 2.\quad\halmos$$

18. Give counterexamples to the following statements:

(a) "If $x, y \in \real$ and $x \le y$ , then $\sin x \le \sin y$ ."

(b) "If $a, b, c, d \in \real$ and $a \le b$ and $c \le d$ , then $ac \le bd$ ."

(a) $\dfrac{\pi}{2} < \pi$ (so $\dfrac{\pi}{2} \le \pi$ ), but $\sin \dfrac{\pi}{2} = 1$ and $\sin \pi = 0$ . Therefore, $\sin \dfrac{\pi}{2} \not\le \sin \pi$ .

(b) $-1 < 0$ (so $-1 \le 0$ ) and $-2 < -1$ (so $-2 \le -1$ ), but $(-1)(-2) = 2$ , while $(0)(-1) = 0$ . Therefore, $(-1)(-2) \not\le (0)(-1)$ .

19. Give a counterexample to the following statement: "If $x^2 - 4 x + 3 = 0$ , then $x = 1$ ."

A counterexample must make the "if-then" statement false. An "if-then" statement is false exactly when the "if" part is true and the "then" part is false.

If $x = 3$ , then $x^2 - 4 x + 3 = 9 - 12 + 3 = 0$ . Thus, the "if" part is true. But since $x = 3 \ne 1$ , the "then" part is false. Therefore, $x = 3$ is a counterexample to the original statement.

20. Suppose the universe is $U = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}$ , and:

$A = \{1, 2, 3, 4, 5\}$ ,

$B = \{2, 4, 6, 8, 10\}$ ,

$C = \{1, 3, 5, 7, 9\}$ .

(a) List the elements of $\complement{A}$ .

(b) List the elements of $A \cap C$ .

(c) List the elements of $A \cup B$ .

(d) List the elements of $(A \cup C) - B$ .

(a)

$$\complement{A} = \{6, 7, 8, 9, 10\}.\quad\halmos$$

(b)

$$A \cap C = \{1, 3, 5\}.\quad\halmos$$

(c)

$$A \cup B = \{1, 2, 3, 4, 5, 6, 8, 10\}.\quad\halmos$$

(d)

$$(A \cup C) - B = \{1, 3, 5, 7, 9\}.\quad\halmos$$

21. Construct Venn diagrams for the following sets:

(a) $A - (B - C)$

(b) $A \cap (B \cup C)$

(a)

$$\hbox{\epsfysize=1.75in \epsffile{rev2-7a.eps}}\quad\halmos$$

(b)

$$\hbox{\epsfysize=1.75in \epsffile{rev2-7b.eps}}\quad\halmos$$

22. What sets are represented by the shaded regions in the following Venn diagrams?

$$\matrix{\hbox{\epsfysize=1.75in \epsffile{rev2-8a.eps}} & \hbox{\epsfysize=1.75in \epsffile{rev2-8b.eps}} \cr {\rm (a)} & {\rm (b)} \cr}$$

There are many possible answers; here are two.

(a) $(A \cap B) \cup (A \cap C) \cup (B \cap C)$

(b) $[(A \cap C) \cup (B \cap C)] - (A \cap B \cap C)$

23. (a) List the elements of the set $\{a, \{b,c\}\}$ .

(b) List the elements of the set $\{\{d\}\}$ .

(c) Is $\{a,b\}$ a subset of $\{a, \{b,c\}\}$ ? Why or why not?

(a) The elements are a and $\{b,c\}$ .

(b) The only element of $\{\{d\}\}$ is $\{d\}$ .

(c) $\{a,b\}$ is not a subset of $\{a, \{b,c\}\}$ : b is an element of $\{a,b\}$ , but it is not an element of $\{a, \{b,c\}\}$ .

24. (a) Suppose $A = \{1, a, \emptyset\}$ . List the elements of $\powerset(A)$ .

(b) How many subsets does the set $\{n \in \natural \mid 2 \le n \le 10\}$ have?

(a)

$$\powerset(A) = \{\emptyset, \{1\}, \{a\}, \{\emptyset\}, \{1, a\}, \{1, \emptyset\}, \{a, \emptyset\}, \{1, a, \emptyset\}\}.\quad\halmos$$

(b) The set has 9 elements (not 8!), so it has $2^9 = 512$ subsets.

25. (a) Suppose $X = \{a, b\}$ and $Y = \{1, 2, 42\}$ . List the elements of $X \times Y$ .

(b) Are the sets $\{1, 2\}$ and $\{2, 1\}$ equal? Are the ordered pairs$(1, 2)$ and $(2, 1)$ equal?

(c) Suppose $|X| = 5$ and $|Y| = 4$ . Find $|X \times Y|$ and $|\powerset(X \times Y)|$ .

(a)

$$X \times Y = \{(a, 1), (a, 2), (a, 42), (b, 1), (b, 2), (b, 42)\}. \quad\halmos$$

(b) $\{1, 2\} = \{2, 1\}$ , because the sets have the same elements. The order in which the elements are listed doesn't matter.

$(1, 2) \ne (2, 1)$ because ordered pairs are equal if and only if their first components are equal and their second components are equal. These two pairs have different first components ($1 \ne 2$ ) and different second components ($2 \ne 1$ ).

(c) First,

$$|X \times Y| = |X| \cdot |Y| = 5 \cdot 4 = 20.$$

Next,

$$|\powerset(X \times Y)| = 2^{|X \times Y|} = 2^{20} = 1048576. \quad\halmos$$

26. Let A, B, and C be sets. Prove that

$$A \cap B \subset (A \cup C) \cap (B \cup C).$$

Let $x \in A \cap B$ . I must show that $x \in (A \cup C) \cap (B \cup C)$ .

$$\matrix{ x \in A \cap B & \ifthen & x \in A \land x \in B & \hbox{(Definition of intersection)} \cr & \ifthen & (x \in A \lor x \in C) \land (x \in B \lor x \in C) & \hbox{(Constructing disjunctions)} \cr & \ifthen & (x \in A \cup C) \land (x \in B \cup C) & \hbox{(Definition of union)} \cr & \ifthen & x \in (A \cup C) \cap (B \cup C) & \hbox{(Definition of intersection)} \cr}$$

This proves that $A \cap B \subset (A \cup C) \cap (B \cup C)$ .

27. Let A, B, and C be sets. Prove that

$$(C - A) \cup B = (A \cap B) \cup \left[(C \cup B) - A\right].$$

I'll show each set is contained in the other.

First, I'll show $(C - A) \cup B \subset (A \cap B) \cup \left[(C \cup B) - A\right]$ .

Let $x \in (C - A) \cup B$ . Then $x \in C - A$ or $x \in B$ .

Suppose $x \in C - A$ . Then $x \in C$ , so $x \in C \cup B$ and $x \notin A$ , so $x \in (C \cup B) - A$ . Hence, $x \in (A \cap B) \cup \left[(C \cup B) - A\right]$ .

Suppose $x \in B$ . If $x \in A$ , then $x \in A \cap B$ , so $x \in (A \cap B) \cup \left[(C \cup B) - A\right]$ .

Otherwise, $x \notin A$ . Now $x \in B$ , so $x \in C \cup B$ . Hence, $x \in (C \cup B) - A$ . Therefore, $x \in (A \cap B) \cup \left[(C \cup B) - A\right]$ .

Thus, $x \in (A \cap B) \cup \left[(C \cup B) - A\right]$ in every case, so $(C - A) \cup B \subset (A \cap B) \cup \left[(C \cup B) - A\right]$ .

Conversely, suppose $x \in (A \cap B) \cup \left[(C \cup B) - A\right]$ . Then $x \in (A \cap B)$ or $x \in (C \cup B) - A$ .

Suppose $x \in (A \cap B)$ . Then $x \in B$ , so $x \in (C - A) \cup B$ .

Alternatively, suppose $x \in (C \cup B) - A$ . Then $x \in (C \cup B)$ and $x \notin A$ . Now $x \in (C \cup B)$ means $x \in C$ or $x \in B$ .

In the first case, $x \in C$ and $x \notin A$ give $x \in C - A$ , so $x \in (C - A) \cup B$ .

In the second case, $x \in B$ gives $x \in (C - A) \cup B$ .

In every case, $x \in (C - A) \cup B$ , so $(A \cap B) \cup \left[(C \cup B) - A\right] \subset (C - A) \cup B$ .

Therefore, $(C - A) \cup B = (A \cap B) \cup \left[(C \cup B) - A\right]$ .

Here is a more formal layout of the proof, with the logical connectives written explicitly.

$$\matrix{x \in \left((A \cap B) \cup \left[(C \cup B) - A\right]\right) & \iff & x \in (A \cap B) \lor x \in \left[(C \cup B) - A\right] \hfill \cr & & \hskip0.5in \hbox{Definition of $\cup$} \hfill \cr & \iff & (x \in A \land x \in B) \lor \left[x \in (C \cup B) \land x \notin A\right] \hfill \cr & & \hskip0.5in \hbox{Definitions of $\cap$, complement} \hfill \cr & \iff & (x \in A \land x \in B) \lor \left[(x \in C \cup x \in B) \land x \notin A\right] \hfill \cr & & \hskip0.5in \hbox{Definition of $\cup$} \hfill \cr & \iff & (x \in A \land x \in B) \lor \left[(x \in C \land x \notin A) \lor (x \in B \land x \notin A)\right] \hfill \cr & & \hskip0.5in \hbox{Distributivity} \hfill \cr & \iff & (x \in C \land x \notin A) \lor (x \notin A \land x \in B) \lor (x \in A \land x \in B) \hfill \cr & & \hskip0.5in \hbox{Commutativity} \hfill \cr & \iff & (x \in C \land x \notin A) \lor \left[(x \notin A \lor x \in A) \land x \in B\right] \hfill \cr & & \hskip0.5in \hbox{Distributivity} \hfill \cr & \iff & (x \in C \land x \notin A) \lor x \in B \hfill \cr & & \hskip0.5in \hbox{$(x \notin A \lor x \in A)$ is tautologous} \hfill \cr & \iff & x \in (C - A) \lor x \in B \hfill \cr & & \hskip0.5in \hbox{Definition of complement} \hfill \cr & \iff & x \in [(C - A) \cup B] \hfill \cr & & \hskip0.5in \hbox{Definition of $\cup$} \hfill \cr}$$

This proves that $(C - A) \cup B = (A \cap B) \cup \left[(C \cup B) - A\right]$ .

28. Let A and B be sets. Prove that

$$(A - B) \cap (B - A) = \emptyset.$$

Since the empty set is a subset of every set, I know that $\emptyset \subset (A - B) \cap (B - A)$ .

Next, I'll show that $(A - B) \cap (B - A) \subset \emptyset$ . Taking elements, I have to show that if $x \in (A - B) \cap (B - A)$ , then $x \in \emptyset$ . (Actually, I'll show that this conditional statement is vacuously true by showing that the "if" part is false.)

$$\matrix{ x \in (A - B) \cap (B - A) & \ifthen & x \in (A - B) \land x \in (B - A) & \hbox{(Definition of intersection)} \cr & \ifthen & x \in A \land \lnot x \in B \land x \in B \land \lnot x \in A & \hbox{(Definition of complement)} \cr & \ifthen & (x \in A \land \lnot x \in A) \land (x \in B \land \lnot x \in B) & \hbox{(Commutativity)} \cr & \ifthen & \hbox{(False)} \land \hbox{(False)} & \hbox{(Contradiction)} \cr & \ifthen & \hbox{(False)} & \hbox{(Truth table for $\land$)} \cr}$$

By proof by contradiction, the statement $x \in (A - B) \cap (B - A)$ is false. This makes the conditional statement "if $x \in (A - B) \cap (B - A)$ , then $x \in \emptyset$ " true! Hence, $(A - B) \cap (B - A) \subset \emptyset$ .

Since $(A - B) \cap (B - A) \subset \emptyset$ and $\emptyset \subset (A - B) \cap (B - A)$ , it follows that $(A - B) \cap (B - A) = \emptyset$ .

29. Let A and B be sets.

(a) Prove that $A \subset A \cup B$ and $B \subset A \cup B$ .

(b) Prove that $A \cup B = B$ if and only if $A \subset B$ .

(a) Let $x \in A$ . Then $x \in A$ or $x \in B$ (the logical rule is "constructing a disjunction"), so $x \in A \cup B$ . Therefore, $A \subset A \cup B$ .

Let $x \in B$ . Then $x \in A$ or $x \in B$ (the logical rule is "constructing a disjunction"), so $x \in A \cup B$ . Therefore, $B \subset A \cup B$ .

(b) Suppose $A \cup B = B$ . I want to show $A \subset B$ .

Let $x \in A$ . Then by (a), $x \in A \subset A \cup B = B$ . Hence, $A \subset B$ .

Suppose $A \subset B$ . I want to show $A \cup B = B$ .

I will show each of the sets $A \cup B$ and B is contained in the other.

First, by (a) $B \subset A \cup B$ .

On the other hand, let $x \in A \cup B$ . This means that either $x \in A$ or $x \in B$ . In the first case, $x \in A \subset B$ . In the second case, $x \in B$ . So in either case, $x \in B$ . This proves $A \cup B \subset B$ .

This proves that $A \cup B = B$ .

30. Recall that

$$(a, b) = \{x \in \real \mid x > a \land x < b\}.$$

Prove that $(1, 3) \cap (2, 4) = (2, 3)$ .

I'll show that $(1, 3) \cap (2, 4) \subset (2, 3)$ and $(2, 3) \subset (1, 3) \cap (2, 4)$ .

Suppose $x \in (1, 3) \cap (2, 4)$ . Then by the definition of intersection, $x \in (1, 3)$ and $x \in (2, 4)$ . By the interval definition, this means that $1 < x$ and $x < 3$ and $2 < x$ and $x < 4$ .

In particular, $x < 3$ and $2 < x$ , so by the interval definition $x \in (2, 3)$ .

This proves that $(1, 3) \cap (2, 4) \subset (2, 3)$ .

Conversely, suppose $x \in (2, 3)$ , so by the interval definition $2 < x$ and $x < 3$ .

First, $x < 3 < 4$ . Together with $2 < x$ , this means by the interval definition that $x \in (2, 4)$ .

Second, $1 < 2 < x$ . Together with $x < 3$ , this means by the interval definition that $x \in (1, 3)$ .

By the definition of intersection, $x \in (1, 3) \cap (2, 4)$ .

This proves that $(2, 3) \subset (1, 3) \cap (2, 4)$ .

Therefore, $(1, 3) \cap (2, 4) = (2, 3)$ .

31. Recall that

$$[a, b] = \{x \in \real \mid x \ge a \land x \le b\}.$$

Prove that $[-2, 3] \cup [1, 5] = [-2, 5]$ .

Suppose $x \in [-2, 3] \cup [1, 5]$ . Then by the definition of union, $x \in [-2, 3]$ or $x \in [1, 5]$ .

If $x \in [-2, 3]$ , then by the interval definition $x \ge -2$ and $x \le 3$ . Now $3 < 5$ , so $x \le 5$ . Since $x \ge -2$ and $x \le 5$ , by the interval definition $x \in [-2, 5]$ .

If $x \in [1, 5]$ , then by the interval definition $x \ge 1$ and $x \le 5$ . Now $-2 < 1$ , so $x \ge -2$ . Since $x \ge -2$ and $x \le 5$ , by the interval definition $x \in [-2, 5]$ .

This proves that $[-2, 3] \cup [1, 5] \subset [-2, 5]$ .

For the opposite inclusion, suppose $x \in [-2, 5]$ . By the interval definition, $x \ge -2$ and $x \le 5$ . Consider two cases.

First, suppose $x \le 2$ . Since $2 < 3$ , it follows that $x \le 3$ . Since $x \ge -2$ and $x \le 3$ , by the interval definition $x \in [-2, 3]$ . By the definition of union, $x \in [-2, 3] \cup [1, 5]$ .

Second, suppose $x > 2$ . Now $2 > 1$ , so $x \ge 1$ . Since $x \ge 1$ and $x \le 5$ , by the interval definition $x \in [1, 5]$ . By the definition of union, $x \in [-2, 3] \cup [1, 5]$ .

This proves that $[-2, 5] \subset [-2, 3] \cup [1, 5]$ .

Hence, $[-2, 3] \cup [1, 5] = [-2, 5]$ .

32. Suppose $S = \{1, 2\}$ and $T = \{a, b\}$ . List the elements of $S \times T$ and $T \times S$ .

$$S \times T = \{(1,a), (1,b), (2,a), (2,b)\} \quad\hbox{while}\quad T \times S = \{(a,1), (a,2), (b,1), (b,2)\}.\quad\halmos$$

33. Give a specific example of two sets A and B for which $A \times B \ne B \times A$ .

For example, let $A = \{a, b\}$ and $B = \{3, 4\}$ . Then

$$A \times B = \{(a, 3), (a, 4), (b, 3), (b, 4)\} \quad\hbox{and}\quad B \times A = \{(3, a), (3, b) (4, a), (4, b)\}.$$

The two sets are not the same.

34. Prove using the limit definition that

$$\lim_{n \to \infty} \dfrac{3 n + 5}{n + 1} = 3.$$

Let $\epsilon > 0$ . Set $M = \max \left(0, \dfrac{2}{\epsilon} - 1\right)$ . If $n > M$ , then I have

$$n > 0 \quad\hbox{and}\quad n > \dfrac{2}{\epsilon} - 1.$$

Hence,

$$\eqalign{ n & > \dfrac{2}{\epsilon} - 1 \cr \noalign{\vskip2pt} n + 1 & > \dfrac{2}{\epsilon} \cr \noalign{\vskip2pt} \epsilon(n + 1) & > 2 \cr}$$

Since $n > 0$ , I have $n + 1 > 0$ , so I may divide both sides by $n + 1$ , then insert absolute values signs:

$$\eqalign{ \epsilon & > \dfrac{2}{n + 1} \cr \noalign{\vskip2pt} \epsilon & > \left|\dfrac{2}{n + 1}\right| \cr \noalign{\vskip2pt} \epsilon & > \left|\dfrac{(3 n + 5) - 3(n + 1)}{n + 1}\right| \cr \noalign{\vskip2pt} \epsilon & > \left|\dfrac{3 n + 5}{n + 1} - 3\right| \cr}$$

This proves that $\displaystyle \lim_{n \to \infty} \dfrac{3 n + 5}{n + 1} = 3$ .

35. Prove using the limit definition that

$$\lim_{n \to \infty} \dfrac{10 n}{2 n + 1} = 5.$$

Let $\epsilon > 0$ . Set $M = \max \left(0, \dfrac{5}{2\epsilon} - \dfrac{1}{2}\right)$ . If $n > M$ , then I have

$$n > 0 \quad\hbox{and}\quad n > \dfrac{5}{2\epsilon} - \dfrac{1}{2}.$$

Hence,

$$\eqalign{ n & > \dfrac{5}{2\epsilon} - \dfrac{1}{2} \cr 2 n & > \dfrac{5}{\epsilon} - 1 \cr 2 n + 1 & > \dfrac{5}{\epsilon} \cr}$$

Sine $n > 0$ , I have $2 n + 1 > 0$ , so I may multiply both sides by $\dfrac{\epsilon}{2 n + 1}$ to get

$$\epsilon > \dfrac{5}{2 n + 1}.$$

Again, since $2 n + 1 > 0$ , I may insert absolute value signs on the right and obtain

$$\eqalign{ \epsilon & > \left|\dfrac{5}{2 n + 1}\right| \cr \epsilon & > \left|\dfrac{-5}{2 n + 1}\right| \cr \epsilon & > \left|\dfrac{10 n - 5(2 n + 1)}{2 n + 1}\right| \cr \epsilon & > \left|\dfrac{10 n}{2 n + 1} - 5\right| \cr}$$

This proves that

$$\lim_{n \to \infty} \dfrac{10 n}{2 n + 1} = 5.\quad\halmos$$

He who has overcome his fears will truly be free. - Aristotle

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga