Review Problems for the Final

Math 393

These problems are intended to help you study. The fact that a problem occurs here does not mean that there will be a similar problem on the test. And the absence of a problem from this review sheet does not mean that there won't be a problem of that kind on the test.

1. Find the coefficient of $x^{16}y^{15}$ in the expansion of $(2 x^2 + y^3)^{13}$ .

2. Find the number of elements of $\{1, 2, \ldots 2000\}$ which are divisible by either 8 or by 22.

3. Prove that if $n \in \integer^+$ , then $12 \mid n^4 - n^2$ .

4. Define

$$x_1 = 1, \quad x_k = 1 + x_1 x_2 \cdots x_{k-1} \quad\hbox{for}\quad k > 1.$$

Prove that for $n \ge 1$ ,

$$\sum_{k=1}^n \dfrac{1}{x_k} = 2 - \dfrac{1}{x_1 x_2 \cdots x_n}.$$

5. Let $f_n$ denote the $n^{\rm th}$ Fibonacci number. Simplify $f_{3 n + 10} - f_{3 n + 7} - f_{3 n + 8}$ to a single Fibonacci number, assuming that $n \ge 0$ .

6. Find all integers $n \in \integer^+$ such that $n + 1 \mid n^2 + 1$ .

7. Find $(387, 927)$ and express it as an integer linear combination of 387 and 927.

8. Find all pairs of positive integers $(m, n)$ such that

$$[m, n] - (m, n) = 65.$$

9. (a) Explain why the Diophantine equation $6 x + 14 y = 7$ has no solutions.

(b) Solve the Diophantine equation $6 x + 25 y = 7$ .

10. Solve the Diophantine equation $x^2 + 2 y^2 = 3 x y + 2$ .

11. Find all integer solutions (positive or negative) to the Diophantine equation $x^2 + 4 y^2 = 17$ .

12. Use Fermat factorization to factor 43621.

13. Solve the system of congruences

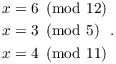
$$\eqalign{ x & = 6 \mod{12} \cr x & = 3 \mod{5} \cr x & = 4 \mod{11} \cr}.$$

14. Solve $3 x + 4 y = 7 \mod{8}$ . Include ranges for the parameters which give all the distinct solutions mod 8, without duplication.

15. If n is an integer, can $n^4 + n^2 + 1$ be divisible by 5?

16. Prove that if $x = a \mod{b}$ , $x = a \mod{c}$ , and $(b, c) = 1$ , then $x = a \mod{b c}$ .

17. (a) List the numbers in $\{0, 1, 2, 3, 4, 5, 6, 7, 8\}$ which are invertible mod 9.

(b) A number $u \in \{0, 1, \ldots, n - 1\}$ which is invertible mod n is a primitive root mod n if the powers u, $u^2$ , $u^3$ , ... of u give all the numbers which are invertible mod n. Show that 2 is a primitive root mod 9.

(c) Show by computation that there is no primitive root mod 8.

18. 2063 and 3041 are primes. Prove without computation that

$$2063^{3040} + 3041^{2062} = 1 \mod{2063 \cdot 3041}.$$

19. Reduce $\dfrac{5062!}{5002!}$ mod 61 to a number in the range $\{0, 1, \ldots, 60\}$ .

20. Solve the system of congruences

$$\matrix{ 2 x & + & 3 y & = & 4 \mod{5} \cr x & + & 2 y & = & 3 \mod{5} \cr}.$$

21. Compute $\phi(864)$ , $\sigma(864)$ , and $\tau(864)$ .

22. Calvin Butterball says: "If $n > 1$ , the factors of n come in pairs $\{a, b\}$ , where $n = a b$ . Hence, $\tau(n)$ must be even." Is he right?

23. For what positive integers n does $\phi(5 n) = 5\phi(n)$ ?

24. Let $n \ge 2$ . Consider the set S of integers in $\{1, 2, \ldots, n - 1\}$ which are relatively prime to n. Prove that the sum of the elements of S is $\dfrac{n \cdot \phi(n)}{2}$ .

25. Find the last three digits of $7^{8403}$ .

26. Show that if $\sigma(n) = 36$ , then $n = 22$ .

27. Prove that if n is an integer and $3 \notdiv n$ , then $n^{37} - n$ is divisible by 54.

28. Show that $2^{31} - 1$ has no prime factors less than 500.

29. Find the decoding transformation for the block cipher

$$\left[\matrix{c_1 \cr c_2 \cr}\right] = \left[\matrix{ 17 & 3 \cr 5 & 2 \cr}\right] \left[\matrix{p_1 \cr p_2 \cr}\right] \mod{26}.$$

30. Consider the exponential cipher which uses the prime $p = 3121$ and the exponent $e = 11$ .

(a) Encipher the word FOOD.

(b) Find the deciphering transformation.

31. For an RSA cipher, it is known that the modulus is $n = 240181$ , and $\phi(240181) = 239200$ . Find the primes p and q such that $n = p q$ .

32. Find all solutions to the congruence

$$x^2 = 74 \mod{203}.$$

Note: $203 = 7 \cdot 29$ .

33. Find a solution to $x^2 = 208 \mod{289}$ by lifting a solution to the congruence mod 17.

34. Suppose that p is an odd prime and $p = 19 \mod{20}$ . Compute $\legendre{-5}{p}$ .

35. Compute $\legendre{180}{211}$ .

36. Compute $\legendre{375}{461}$ .

37. Convert $(5573)_6$ to base 10.

38. Convert 2781 to base 5.

39. Express 0.26 in base 5.

40. Find a decimal fraction in lowest terms equal to $(0.2\overline{56})_7$ .

41. Express $(.1\overline{25})_6$ as a decimal fraction in lowest terms.

42. If b is an integer and $b > 1$ , find a decimal fraction equal to $(0.\overline{1})_b$ .

43. Find the finite continued fraction expansion for $\dfrac{271}{43}$ .

44. (a) Find the first 5 convergents of $[7; \overline{5, 10}]$ .

(b) Find the exact value of $x = [7; \overline{5, 10}]$ .

45. Find the first 10 terms of the continued fraction expansion of $\root 3 \of {114}$ .

46. (a) Find the continued fraction expansion of $\sqrt{7}$ . Find the convergents $c_0$ , ..., $c_8$ .

(b) Use the convergents of the continued fraction expansion of $\sqrt{7}$ to find a solution to the Fermat-Pell equation $x^2 - 7 y^2 = 1$ .

47. Find the convergents of the finite continued fraction $[1;1, 4, 1, 4, 1, 4]$ .

48. Find the exact value of the periodic continued fraction $[1;\overline{2, 5}]$ .

49. Find the rational number $\dfrac{p}{q}$ in lowest terms with $q \le 50$ which best approximates $\dfrac{\pi}{e}$ .

Solutions to the Review Problems for the Final

1. Find the coefficient of $x^{16}y^{15}$ in the expansion of $(2 x^2 + y^3)^{13}$ .

I'll get a $x^{16}y^{15}$ term by taking $(2 x^2)^8$ and $(y^3)^5$ . Thus, the coefficient is ${{13} \choose 8}\cdot 2^8 = 329472$ .

2. Find the number of elements of $\{1, 2, \ldots 2000\}$ which are divisible by either 8 or by 22.

The number of elements of $\{1, 2, \ldots 2000\}$ which are divisible by 8 is

$$\left[\dfrac{2000}{8}\right] = 250.$$

The number of elements of $\{1, 2, \ldots 2000\}$ which are divisible by 22 is

$$\left[\dfrac{2000}{22}\right] = [90.90909 \ldots] = 90.$$

The number of elements of $\{1, 2, \ldots 2000\}$ which are divisible by both 8 and 22 is the number divisible by their least common multiple, and $[8, 22] = 88$ . The number of elements of $\{1, 2, \ldots 2000\}$ which are divisible by 88 is

$$\left[\matrix{2000}{88}\right] = [22.72727 \ldots] = 22.$$

The number divisible by both is counted in both the number divisible by 8 and the number divisible by 22. So it must be subtracted off once to get the number divisible by either 8 or 22:

$$250 + 90 - 22 = 318.\quad\halmos$$

3. Prove that if $n \in \integer^+$ , then $12 \mid n^4 - n^2$ .

For $n = 1$ , I have $n^4 - n^2 = 1^4 - 1^2 = 0$ , and $12 \mid 0$ .

Suppose $12 \mid n^4 - n^2$ . I want to show that $12 \mid (n + 1)^4 - (n + 1)^2$ . Now

$$\eqalign{ (n + 1)^4 - (n + 1)^2 & = (n^4 + 4 n^3 + 6 n^2 + 4 n + 1) - (n^2 + 2 n + 1) \cr & = (n^4 - n^2) + (4 n^3 + 6 n^2 + 2 n) \cr & = (n^4 - n^2) + 2 n(2 n^2 + 3 n + 1) \cr & = (n^4 - n^2) + 2 n(n + 1)(2 n + 1) \cr}$$

I know that $12 \mid n^4 - n^2$ by induction.

To show that $12 \mid 2 n(n + 1)(2 n + 1)$ , you can take several approaches. One approach is to consider $n = 0, 1, \ldots, 11$ mod 12 and show that you always get 0. A sneakier approach is to note that

$$\eqalign{ 1^2 + 2^2 + 3^2 + \cdots + n^2 & = \dfrac{n(n + 1)(2 n + 1)}{6} \cr 12(1^2 + 2^2 + 3^2 + \cdots + n^2) & = 2 n(n + 1)(2 n + 1) \cr}$$

In any event, since $12 \mid n^4 - n^2$ and $12 \mid 2 n(n + 1)(2 n + 1)$ , I have $12 \mid (n + 1)^4 - (n + 1)^2$ . This completes the induction step and the proof.

4. Define

$$x_1 = 1, \quad x_k = 1 + x_1 x_2 \cdots x_{k-1} \quad\hbox{for}\quad k > 1.$$

Prove that for $n \ge 1$ ,

$$\sum_{k=1}^n \dfrac{1}{x_k} = 2 - \dfrac{1}{x_1 x_2 \cdots x_n}.$$

For $n = 1$ ,

$$\sum_{k=1}^1 \dfrac{1}{x_k} = \dfrac{1}{x_1} = \dfrac{1}{1} = 1,$$

$$2 - \dfrac{1}{x_1} = 2 - \dfrac{1}{1} = 1.$$

The result is true for $n = 1$ .

Let $n > 1$ , and assume that the result holds for $n - 1$ :

$$\sum_{k=1}^{n-1} \dfrac{1}{x_k} = 2 - \dfrac{1}{x_1 x_2 \cdots x_{n-1}}.$$

Then

$$\sum_{k=1}^n \dfrac{1}{x_k} = \sum_{k=1}^{n-1} \dfrac{1}{x_k} + \dfrac{1}{x_n} = 2 - \dfrac{1}{x_1 x_2 \cdots x_{n-1}} + \dfrac{1}{x_n} =$$

$$2 - \dfrac{x_n - x_1 x_2 \cdots x_{n-1}}{x_1 x_2 \cdots x_{n-1} x_n} = 2 - \dfrac{1}{x_1 x_2 \cdots x_{n-1} x_n}.$$

(The second equality used the induction hypothesis, the third equality came from combining fractions over a common denominator, and the fourth equality came from the definition of the x's.)

Therefore, the result holds for n, so it's true for all $n \ge 1$ , by induction.

5. Let $f_n$ denote the $n^{\rm th}$ Fibonacci number. Simplify $f_{3 n + 10} - f_{3 n + 7} - f_{3 n + 8}$ to a single Fibonacci number, assuming that $n \ge 0$ .

$$f_{3 n + 10} - f_{3 n + 7} - f_{3 n + 8} = f_{3 n + 10} - (f_{3 n + 7} + f_{3 n + 8}) = f_{3 n + 10} - f_{3 n + 9} = f_{3 n + 8}.\quad\halmos$$

6. Find all integers $n \in \integer^+$ such that $n + 1 \mid n^2 + 1$ .

Suppose $n + 1 \mid n^2 + 1$ . Then

$$n + 1 \mid n^2 + 1 = (n^2 + 2 n + 1) - 2 n = (n + 1)^2 - 2 n.$$

But $n + 1 \mid (n + 1)^2$ , so $n + 1 \mid 2 n$ .

Say $k(n + 1) = 2 n$ , where $k \in \integer^+$ . If $k \ge 2$ , then

$$\eqalign{ k(n + 1) & \ge 2(n + 1) \cr 2 n & \ge 2(n + 1) \cr 2 n & \ge 2(n + 1) > 2 n \cr}$$

This is a contradiction. Hence, $k = 1$ . This means that $1(n + 1) = 2 n$ , so $n = 1$ .

7. Find $(387, 927)$ and express it as an integer linear combination of 387 and 927.

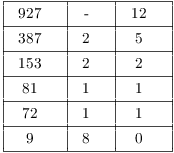
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 927 & & - & & 12 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 387 & & 2 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 153 & & 2 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 81 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 72 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 9 & & 8 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$(-5)(927) + (12)(387) = 9 = (387, 927).\quad\halmos$$

8. Find all pairs of positive integers $(m, n)$ such that

$$[m, n] - (m, n) = 65.$$

Note that $(m, n) \mid m \mid [m, n]$ . Hence,

$$(m, n) \mid [m, n] - (m, n) = 65.$$

Now 65 has 4 positive divisors: 1, 5, 13, and 65. I consider each of these cases.

Case 1. $(m, n) = 1$ .

Using $[m, n] = \dfrac{m n}{(m, n)}$ , I get $[m, n] = m n$ . So

$$\eqalign{ [m, n] - (m, n) & = 65 \cr m n - 1 & = 65 \cr m n & = 66 \cr}$$

m and n are relatively prime ($(m, n) = 1$ ) positive integers whose product is 66. This gives me the following pairs (ignoring order):

$$(m, n) = (1, 66), \quad (2, 33), \quad (3, 22), \quad (6, 11).$$

Case 2. $(m, n) = 5$ .

$(m, n) \mid m$ , so $m = (m, n) a = 5 a$ . Likewise, $(m, n) \mid n$ , so $n = (m, n) b = 5 b$ . Since I've divided m and n by their greatest common divisor, I must have $(a, b) = 1$ .

Moreover,

$$[m, n] = \dfrac{m n}{(m, n)} = \dfrac{(5 a)(5 b)}{5} = 5 a b.$$

So

$$\eqalign{ [m, n] - (m, n) & = 65 \cr 5 a b - 5 & = 65 \cr 5 a b & = 70 \cr a b & = 14 \cr}$$

a and b are relatively prime positive integers whose product is 14. This gives me the following pairs (ignoring order):

$$(a, b) = (1, 14), \quad (2, 7).$$

If $(a, b) = (1, 14)$ , then multiplying by 5 gives $(m, n) = (5, 70)$ .

If $(a, b) = (2, 7)$ , then multiplying by 5 gives $(m, n) = (10, 35)$ .

Case 3. $(m, n) = 13$ .

$(m, n) \mid m$ , so $m = (m, n) a = 13 a$ . Likewise, $(m, n) \mid n$ , so $n = (m, n) b = 13 b$ . Since I've divided m and n by their greatest common divisor, I must have $(a, b) = 1$ .

Moreover,

$$[m, n] = \dfrac{m n}{(m, n)} = \dfrac{(13 a)(13 b)}{13} = 13 a b.$$

So

$$\eqalign{ [m, n] - (m, n) & = 65 \cr 13 a b - 13 & = 65 \cr 13 a b & = 78 \cr a b & = 6 \cr}$$

a and b are relatively prime positive integers whose product is 6. This gives me the following pairs (ignoring order):

$$(a, b) = (1, 6), \quad (2, 3).$$

If $(a, b) = (1, 6)$ , then multiplying by 13 gives $(m, n) = (13, 78)$ .

If $(a, b) = (2, 3)$ , then multiplying by 13 gives $(m, n) = (26, 39)$ .

Case 4. $(m, n) = 65$ .

$(m, n) \mid m$ , so $m = (m, n) a = 65 a$ . Likewise, $(m, n) \mid n$ , so $n = (m, n) b = 65 b$ . Since I've divided m and n by their greatest common divisor, I must have $(a, b) = 1$ .

Moreover,

$$[m, n] = \dfrac{m n}{(m, n)} = \dfrac{(65 a)(65 b)}{65} = 65 a b.$$

So

$$\eqalign{ [m, n] - (m, n) & = 65 \cr 65 a b - 65 & = 65 \cr 65 a b & = 130 \cr a b & = 2 \cr}$$

a and b are relatively prime positive integers whose product is 2. The only solution (ignoring order) is $(a, b) = (1, 2)$ .

If $(a, b) = (1, 2)$ , then multiplying by 65 gives $(m, n) = (65, 130)$ .

All together, the solutions are:

$$(m, n) = (1, 66), \quad (2, 33), \quad (3, 22), \quad (6, 11), \quad (5, 70), \quad (10, 35), \quad (13, 78), \quad (26, 39), \quad (65, 130).\quad\halmos$$

9. (a) Explain why the Diophantine equation $6 x + 14 y = 7$ has no solutions.

(b) Solve the Diophantine equation $6 x + 25 y = 7$ .

(a) If $(x, y)$ is a solution, then $2 \mid 6 x + 14 y$ , but $2 \notdiv 7$ , contradicting the fact that $6 x + 14 y = 7$ .

(b) $(6, 25) = 1 \mid 7$ , so there are solutions.

I could find a particular solution by inspection; instead, I'll do it systematically using the Extended Euclidean algorithm.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 25 & & - & & 4 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 6 & & 4 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 6 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus,

$$(6)(-4) + (25)(1) = 1.$$

Multiply by 7:

$$(6)(-28) + (25)(7) = 7.$$

Thus, $x_0 = -28$ , $y_0 = 7$ is a particular solution. The general solution is

$$x = -28 + 25 s, \quad y = 7 - 6 s.\quad\halmos$$

10. Solve the Diophantine equation $x^2 + 2 y^2 = 3 x y + 2$ .

Rewrite the equation as

$$x^2 - 3 x y + 2 y^2 = 3, \quad\hbox{or}\quad (x - y)(x - 2 y) = 2.$$

There are 4 possibilities, corresponding to the four ways of factoring 2 into a product of 2 integers.

Case 1: $x - y = 1$ and $x - 2 y = 2$ .

Adding the equations gives $y = -1$ , and so $x = 0$ .

Case 2: $x - y = 2$ and $x - 2 y = 1$ .

Adding the equations gives $y = 1$ , and so $x = 3$ .

Case 3: $x - y = -1$ and $x - 2 y = -2$ .

Adding the equations gives $y = 1$ , and so $x = 0$ .

Case 4: $x - y = -2$ and $x - 2 y = -1$ .

Adding the equations gives $y = -1$ , and so $x = -1$ .

The solutions are $(0, -1)$ , $(3, 1)$ , $(0, 1)$ , and $(-1, -1)$ .

11. Find all integer solutions (positive or negative) to the Diophantine equation $x^2 + 4 y^2 = 17$ .

Note that $|x| < \sqrt{17}$ and $|y| < \dfrac{\sqrt{17}}{2}$ , so I can simply check cases. Note also that $4 y^2$ is even and 17 is odd, so $x^2$ must be odd, and hence x must be odd. Finally, if x works, so does $-x$ , and likewise for y and $-y$ . Therefore, I only need to check positive numbers.

Putting all these constraints together, I find that I only need to try $x = 1$ and $x = 3$ .

If $x = 1$ , then $4 y^2 = 17 - x^2 = 16$ , so $y = \pm 2$ . This gives the four solutions $(1, 2)$ , $(1, -2)$ , $(-1, 2)$ , $(-1, -2)$ .

If $x = 3$ , then $4 y^2 = 17 - 9 = 8$ . This has no integer solutions.

The only solutions are $(1, 2)$ , $(1, -2)$ , $(-1, 2)$ , $(-1, -2)$ .

12. Use Fermat factorization to factor 43621.

Since $\sqrt{43621} \approx 208.85641$ , I'll start at $n = 209$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & n & & $n^2 - 43621$ & & $\sqrt{n^2 - 43621}$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 209 & & 60 & & $7.74596 \ldots$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 210 & & 479 & & $21.88606 \ldots$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 211 & & 900 & & 30 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

I have

$$\eqalign{ 30^2 & = 211^2 - 43621 \cr 43621 & = 211^2 - 30^2 \cr 43621 & = (211 + 30)(211 - 30) \cr 43621 & = 241 \cdot 181 \cr}$$

You can check that 241 and 181 are prime.

13. Solve the system of congruences

$$\eqalign{ x & = 6 \mod{12} \cr x & = 3 \mod{5} \cr x & = 4 \mod{11} \cr}.$$

The moduli are relatively prime. The Chinese Remainder Theorem implies that there is a unique solution mod $12 \cdot 5 \cdot 11 = 660$ .

$x = 6 \mod{12}$ implies that $x = 6 + 12 s$ . So

$$\eqalign{ 6 + 12 s & = 3 \mod{5} \cr 1 + 2 s & = 3 \mod{5} \cr 2 s & = 2 \mod{5} \cr s & = 1 \mod{5} \cr}$$

This means that $s = 1 + 5 t$ , so

$$x = 6 + 12(1 + 5 t) = 18 + 60 t.$$

Then

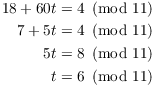
$$\eqalign{ 18 + 60 t & = 4 \mod{11} \cr 7 + 5 t & = 4 \mod{11} \cr 5 t & = 8 \mod{11} \cr t & = 6 \mod{11} \cr}$$

This means that $t = 6 + 11 u$ , so

$$x = 18 + 60(6 + 11 u) = 378 + 660 u.$$

Therefore, $x = 378 \mod{660}$ .

14. Solve $3 x + 4 y = 7 \mod{8}$ . Include ranges for the parameters which give all the distinct solutions mod 8, without duplication.

Since $(3, 4, 8) = 1 \mid 7$ , there are $1 \cdot 8 = 8$ distinct solutions mod 8.

Write the congruence as the Diophantine equation

$$3 x + 4 y + 8 z = 7.$$

Let $w = 3 x + 4 y$ . Then

$$w + 8 z = 7.$$

By inspection, $w_0 = -1$ , $z_0 = 1$ is a particular solution. The general solution is

$$w = -1 + 8 s, \quad z = 1 - s.$$

Therefore,

$$-1 + 8 s = 3 x + 4 y.$$

By inspection, $x_0 = 1$ , $y_0 = -1 + 2 s$ is a particular solution. The general solution is

$$x = 1 + 4 t, \quad y = -1 + 2 s - 3 t.$$

Reducing mod 8,

$$x = 1 + 4 t \mod{8}, \quad y = 7 + 2 s + 5 t \mod{8}.$$

The parameter ranges $t = 0, 1$ , $s = 0, 1, 2, 3$ give the 8 distinct solutions:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & t & & s & & x & & y & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 1 & & 7 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 1 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 2 & & 1 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 3 & & 1 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & 5 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 5 & & 6 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 5 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 3 & & 5 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

15. If n is an integer, can $n^4 + n^2 + 1$ be divisible by 5?

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $n \mod{5}$ & & 0 & & 1 & & 2 & & $3 $ & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $n^4 + n^2 + 1 \mod{5}$ & & 1 & & 3 & & 1 & & 1 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The table shows that for all n, $n^4 + n^2 + 1 \ne 0 \mod{5}$ . Therefore, $n^4 + n^2 + 1$ is never divisible by 5.

16. Prove that if $x = a \mod{b}$ , $x = a \mod{c}$ , and $(b, c) = 1$ , then $x = a \mod{b c}$ .

$x = a \mod{b}$ means that $b \mid x - a$ and $x = a \mod{c}$ means that $c \mid x - a$ . Also, $(b, c) = 1$ implies that

$$b m + c n = 1 \quad\hbox{for some}\quad m, n.$$

Multiply by $x - a$ :

$$bm(x - a) + c n(x - a) = x - a.$$

$b \mid b$ and $c \mid x - a$ imply that $b c \mid b m(x - a)$ . Also, $c \mid c$ and $b \mid x - a$ imply that $b c \mid c n(x - a)$ .

Thus,

$$b c \mid b m(x - a) + c n(x - a) = x - a.$$

Hence, $x = a \mod{b c}$ .

17. (a) List the numbers in $\{0, 1, 2, 3, 4, 5, 6, 7, 8\}$ which are invertible mod 9.

(b) A number $u \in \{0, 1, \ldots, n - 1\}$ which is invertible mod n is a primitive root mod n if the powers u, $u^2$ , $u^3$ , ... of u give all the numbers which are invertible mod n. Show that 2 is a primitive root mod 9.

(c) Show by computation that there is no primitive root mod 8.

(a) The numbers which are invertible mod 9 are those which are relatively prime to 9:

$$1, \quad 2, \quad 4, \quad 5, \quad 7, \quad 8.\quad\halmos$$

(b)

$$2^1 = 2, \quad 2^2 = 4, \quad 2^3 = 8, \quad 2^4 = 7, \quad 2^5 = 5, \quad 2^6 = 1.$$

I've gotten all of the numbers in $\{1, 2, 4, 5, 7, 8\}$ by taking powers of 2, so 2 is a primitive root mod 9.

(c) The numbers in $\{0, 1, 2, 3, 4, 5, 6, 7\}$ which are invertible mod 8 are 1, 3, 5, and 7. However,

$$1^2 = 1 \mod{8}, \quad 3^2 = 1 \mod{8}, \quad 5^2 = 1 \mod{8}, \quad 7^2 = 1 \mod{8}.$$

Therefore, you can't get all four of 1, 3, 5, and 7 by taking powers of any of these elements. Hence, there is no primitive root mod 8.

Note: If $n \in \integer^+$ , then n has a primitive root if and only if $n = 1, 2, 4, p^k, 2 p^k$ , where p is an odd prime.

18. 2063 and 3041 are primes. Prove without computation that

$$2063^{3040} + 3041^{2062} = 1 \mod{2063 \cdot 3041}.$$

By Fermat's theorem with the prime 3041,

$$2063^{3040} = 1 \mod{3041}, \quad\hbox{so}\quad 2063^{3040} + 3041^{2062} = 1 \mod{3041}.$$

By Fermat's theorem with the prime 2063,

$$3041^{2062} = 1 \mod{2063}, \quad\hbox{so}\quad 2063^{3040} + 3041^{2062} = 1 \mod{2063}.$$

Since 2063 and 3041 are distinct primes, they're relatively prime. Hence,

$$2063^{3040} + 3041^{2062} = 1 \mod{2063 \cdot 3041}.$$

Remark: This result is true with any two distinct primes in place of 2063 and 3041.

19. Reduce $\dfrac{5062!}{5002!}$ mod 61 to a number in the range $\{0, 1, \ldots, 60\}$ .

$$\dfrac{5062!}{5002!} = 5003 \cdot 5004 \cdots 5062.$$

Since $82 \cdot 61 = 5002$ and $83 \cdot 61 = 5063$ , the numbers 5003, 5004, ..., 5062 must reduce mod 61 to 1, 2, ..., 60. By Wilson's theorem,

$$\dfrac{5062!}{5002!} = 5003 \cdot 5004 \cdots 5062 = 1 \cdot 2 \cdots 60 = 60! = -1 = 60 \mod{61}.\quad\halmos$$

20. Solve the system of congruences

$$\matrix{ 2 x & + & 3 y & = & 4 \mod{5} \cr x & + & 2 y & = & 3 \mod{5} \cr}.$$

Write the system in matrix form:

$$\left[\matrix{2 & 3 \cr 1 & 2 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{4 \cr 3 \cr}\right] \mod{5}.$$

Solve the system by inverting the coefficient matrix:

$$\left[\matrix{x \cr y \cr}\right] = \left[\matrix{2 & 3 \cr 1 & 2 \cr}\right]^{-1} \left[\matrix{4 \cr 3 \cr}\right] = \dfrac{1}{1}\cdot \left[\matrix{2 & 2 \cr 4 & 2 \cr}\right] \left[\matrix{4 \cr 3 \cr}\right] = \left[\matrix{4 \cr 2 \cr}\right] \mod{5}.\quad\halmos$$

Note: You can also solve using Cramer's rule or row reduction. Or you can solve the second equation to get $x = 3 y + 3 \mod{5}$ , and plug this into the first equation and solve for y.

21. Compute $\phi(864)$ , $\sigma(864)$ , and $\tau(864)$

$864 = 2^5 \cdot 3^3$ , so

$$\phi(864) = 864\left(1 - \dfrac{1}{2}\right) \left(1 - \dfrac{1}{3}\right) = 288,$$

$$\sigma(864) = \left(\dfrac{2^6 - 1}{2 - 1}\right) \left(\dfrac{3^4 - 1}{3 - 1}\right) = (63)(40) = 2520,$$

$$\tau(864) = (5 + 1)(3 + 1) = 24.\quad\halmos$$

22. Calvin Butterball says: "If $n > 1$ , the factors of n come in pairs $\{a, b\}$ , where $n = a b$ . Hence, $\tau(n)$ must be even." Is he right?

Calvin is forgetting that a and b could be equal. In fact, $\tau(n)$ is even provided that n is not a perfect square; otherwise, $\tau(n)$ is odd. (Try writing a careful proof of this.) For example $\tau(4) = 3$ .

23. For what positive integers n does $\phi(5 n) = 5\phi(n)$ ?

If $5\notdiv n$ , then $(n, 5) = 1$ , so

$$\phi(5 n) = \phi(5)\phi(n) = 4 \phi(n) \ne 5 \phi(n).$$

On the other hand, suppose $5 \mid n$ . I can write $n = 5^k m$ , where $k \ge 1$ and $(m, 5) = 1$ . Then

$$5 \phi(n) = 5 \phi(5^k m) = 5 \phi(5^k) \phi(m) = 5(5^k - 5^{k-1}) \phi(m) = (5^{k+1} - 5^k) \phi(m),$$

$$\phi(5 n) = \phi(5^{k+1} m) = \phi(5^{k+1}) \phi(m) = (5^{k+1} - 5^k) \phi(m).$$

Therefore, $5 \phi(n) = \phi(5 n)$ .

Hence, $\phi(5 n) = 5 \phi(n)$ if and only if $5 \mid n$ .

24. Let $n \ge 2$ . Consider the set S of integers in $\{1, 2, \ldots, n - 1\}$ which are relatively prime to n. Prove that the sum of the elements of S is $\dfrac{n \cdot \phi(n)}{2}$ .

The case $n = 2$ can be proved directly: The only positive integer in $\{1\}$ relatively prime to 2 is 1, and $\dfrac{2 \cdot \phi(2)}{2} = 1$ .

So assume $n > 2$ .

First, note that if $m \in S$ , then $n - m \in S$ . For

$$(m, n) = (m, n - m) = (m + (n - m), n - m) = (n, n - m).$$

Thus, $(m, n) = 1$ if and only if $(n - m, n) = 1$ .

This means that the integers in S occur in pairs $\{m, n - m\}$ .

I claim that that the elements of such a pair are distinct. Suppose on the contrary that $m = n - m$ , so $m = \dfrac{n}{2}$ .

If n is odd, then $\dfrac{n}{2}$ is not an integer, but m is, and I have a contradiction.

If n is even, then $\dfrac{n}{2}$ is an integer that divides n (since $2 \cdot \dfrac{n}{2} = n$ ). Moreover, since $n > 2$ , I have $\dfrac{n}{2} > 1$ . This means that $\left(\dfrac{n}{2}, n\right) = \dfrac{n}{2} \ne 1$ , so $m = \dfrac{n}{2} \notin S$ , another contradiction.

Thus, S can be broken down into pairs $(m, n - m)$ . The sum of the two elements in each pair is $m + (n - m) = n$ . Since $|S| = \phi(n)$ , there must be $\dfrac{\phi(n)}{2}$ pairs. Therefore, the sum of the elements of S is $n \cdot \dfrac{\phi(n)}{2}$ , as I wanted to show.

25. Find the last three digits of $7^{8403}$ .

$\phi(1000) = 400$ , so by Euler's theorem,

$$7^{8403} = (7^{400})^21 \cdot 7^3 = 1^{21}\cdot 343 = 343 \mod{1000}.$$

The last three digits of $7^{8403}$ are 343.

26. Show that if $\sigma(n) = 36$ , then $n = 22$ .

Write the prime factorization of n:

$$n = p_1^{r_1} p_2^{r_2} \cdots p_k^{r_k}.$$

Then

$$\sigma(n) = (1 + p_1 + \cdots + p_1^{r_1}) (1 + p_2 + \cdots + p_2^{r_2}) \cdots (1 + p_k + \cdots + p_k^{r_k}).$$

Here is a table of values of $1 + p + \cdots + p^n$ for various primes p:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & $n=1$ & & $n=2$ & & $n=3$ & & $n=4$ & & $n=5$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $p=2$ & & 3 & & 7 & & 15 & & 31 & & 63 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $p=3$ & & 4 & & 13 & & 40 & & 121 & & 364 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $p=5$ & & 6 & & 31 & & 156 & & 781 & & 3906 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $p=7$ & & 8 & & 57 & & 400 & & 2801 & & 19608 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $p=11$ & & 12 & & 133 & & 1464 & & 16105 & & 177156 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $p=13$ & & 14 & & 183 & & 2380 & & 30941 & & 402234 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $p=17$ & & 18 & & 307 & & 5220 & & 88741 & & 1508598 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $p=19$ & & 20 & & 381 & & 7240 & & 137561 & & 2613660 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Note that 36 does not occur in the first column, since $36 - 1 = 35$ is not prime. Clearly, the numbers in each row and column increase. Thus, any factors of 36 that could occur must be in the table.

The divisors of 36 that occur in the table are 3, 4, 6, 12, and 18.

18 can't be part of the factorization of $\sigma(n) = 36$ , since I don't have any way of getting a factor of 2.

6 can't be part of the factorization, since I can only get the remaining factor of 6 as 6 or as $2 \cdot 3$ . I can't use 6 a second time, and I can't get a factor of 2.

4 can't be part of the factorization, since I can only get the remaining factor of 9 as 9 or as $3 \cdot 3$ . There is no 9 in the table, and I can't use 3 twice.

The only possibility is that $\sigma(n) = 3 \cdot 12$ ; consulting the table, this means that $n = 2 \cdot 11 = 22$ .

27. Prove that if n is an integer and $3 \notdiv n$ , then $n^{37} - n$ is divisible by 54.

To say that $n^{37} - n$ is divisible by 54 is the same as saying that $n^{37} = n \mod{54}$ . Since $54 = 2 \cdot 27$ and $(2, 27) = 1$ , it suffices to prove that $n^{37} = n \mod{2}$ and $n^{37} = n \mod{27}$ .

Since 2 is prime, $n^2 = n \mod{2}$ by a corollary to Fermat's theorem.

$(n, 27) \mid 27$ , so $(n, 27) = 1, 3, 9, 27$ . If $(n, 27) \ne 1$ , then $3 \mid (n, 27) \mid n$ , which contradicts the assumption that $3 \notdiv n$ . Therefore, $(n, 27) = 1$ .

Hence, I may apply Euler's theorem: $\phi(27) = 18$ , so $n^{18} = 1 \mod{27}$ . Then

$$n^{36} = 1 \mod{27}, \quad\hbox{and}\quad n^{37} = n \mod{27}.$$

Since $n^2 = n \mod{2}$ and $n^{37} = n \mod{27}$ , it follows that $n^{37} = n \mod{54}$ .

Note that the result may not hold if $3 \mid n$ . For example, $9^{37} - 9 = 18 \mod{54}$ .

28. Convert $(5573)_6$ to base 10.

$$\hbox{\epsfysize=1in \epsffile{final-review-1.eps}}$$

Hence, $(5573)_6 = 1305$ .

29. Show that $2^{31} - 1$ has no prime factors less than 500.

Since 31 is prime, divisors of $2^{31} - 1$ have the form $2 \cdot 31 k + 1 = 62 k + 1$ . I check numbers of this form less than 500:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & n & & $62 n + 1$ & & Result & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 63 & & 63 isn't prime & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 125 & & 125 isn't prime & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 3 & & 187 & & 187 isn't prime & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 4 & & 249 & & 249 isn't prime & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 5 & & 311 & & $311 \notdiv 2^{31} - 1$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 6 & & 373 & & $373 \notdiv 2^{31} - 1$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 7 & & 435 & & 435 isn't prime & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 8 & & 497 & & 497 isn't prime & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus, $2^{31} - 1$ has no prime factors less than 500. In fact, $2^{31} - 1$ is prime.

30. Find the decoding transformation for the block cipher

$$\left[\matrix{c_1 \cr c_2 \cr}\right] = \left[\matrix{ 17 & 3 \cr 5 & 2 \cr}\right] \left[\matrix{p_1 \cr p_2 \cr}\right] \mod{26}.$$

The determinant of the coefficient matrix is $17 \cdot 2 - 3 \cdot 5 = 19$ , and $(19, 26) = 1$ . Hence, the matrix is invertible.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 26 & & - & & 11 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 19 & & 1 & & 8 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 7 & & 2 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 5 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\eqalign{ (-8) \cdot 26 + 11 \cdot 19 & = 1 \cr 11 \cdot 19 & = 1 \mod{26} \cr}$$

Hence, $19^{-1} = 11 \mod{26}$ .

Therefore,

$$\left[\matrix{ 17 & 3 \cr 5 & 2 \cr}\right]^{-1} = 11 \cdot \left[\matrix{ 2 & -33 \cr -5 & 17 \cr}\right] = \left[\matrix{ 22 & -343 \cr -55 & 187 \cr}\right] = \left[\matrix{ 22 & 21 \cr 23 & 5 \cr}\right].$$

The decoding transformation is

$$\left[\matrix{p_1 \cr p_2 \cr}\right] = \left[\matrix{ 22 & 21 \cr 23 & 5 \cr}\right] \left[\matrix{c_1 \cr c_2 \cr}\right] \mod{26}.\quad\halmos$$

31. Consider the exponential cipher which uses the prime $p = 3121$ and the exponent $e = 11$ .

(a) Encipher the word FOOD.

(b) Find the deciphering transformation.

(a) Since $2525 < 3121 < 252525$ , I use blocks of two letters. FOOD becomes 0514 1403.

I'll do the first block by way of example. I'll do the computation the way you would do it on a calculator which can't accomodate very big numbers.

$$514^{11} = (514^3)^3(514^2) = (2034)^3(2032) = (2034^2)(2034 \cdot 2032) = (1831)(884) = 1926 \mod{3121}$$.

Similarly,

$$1403^{11} = 592 \mod{3121}.$$

The ciphertext is 1926\ 0592.

(b) I need d such that $de = 1 \mod{3120}$ , i.e. such that $11 d = 1 \mod{3120}$ . Use the Extended Euclidean algorithm:

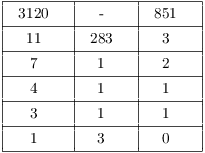
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 3120 & & - & & 851 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 11 & & 283 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 7 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 4 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 3 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 3 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus,

$$(-3)(3120) + (851)(11) = 1 \mod{3120}, \quad\hbox{or}\quad (851)(11) = 1 \mod{3120}.$$

Thus, $d = 851$ , and the decoding transformation is

$$P = C^{851} \mod{3121}.\quad\halmos$$

32. For an RSA cipher, it is known that the modulus is $n = 240181$ , and $\phi(240181) = 239200$ . Find the primes p and q such that $n = p q$ .

Note that

$$\phi(n) = \phi(p q) = (p - 1)(q - 1) = p q - p - q + 1 = n - (p + q) + 1.$$

Thus,

$$p + q = n - \phi(n) + 1 = 240181 - 239200 + 1 = 982.$$

Next,

$$(p - q)^2 = p^2 - 2 p q + q^2 = (p^2 + 2 p q + q^2) - 4 p q = (p + q)^2 - 4 n.$$

Hence,

$$p - q = \sqrt{(p + q)^2 - 4 n} =\sqrt{982^2 - 4 \cdot 240181} = 60.$$

Then

$$p = \dfrac{1}{2}\left((p + q) + (p - q)\right) = \dfrac{1}{2}\left(982 + 60\right) = 521,$$

$$q = \dfrac{1}{2}\left((p + q) - (p - q)\right) = \dfrac{1}{2}\left(982 - 60\right) = 461.\quad\halmos$$

33. Find all solutions to the congruence

$$x^2 = 74 \mod{203}.$$

Note: $203 = 7 \cdot 29$ .

I'll begin by solving the congruence mod 7 and mod 29.

$$x^2 = 74 = 4 \mod{7}.$$

The solutions are obviously $x = 2 \mod{7}$ and $x = -2 = 5 \mod{7}$ .

$$x^2 = 74 = 16 \mod{29}.$$

The solutions are obviously $x = 4 \mod{29}$ and $x = -4 = 25 \mod{29}$ .

(In cases where you couldn't find solutions to these by inspection, you'd probably need to make a table of squares.)

Next, I combine solutions mod 7 with solutions mod 29 using the Chinese Remainder theorem.

First,

$$\eqalign{ x & = 2 \mod{7} \cr x & = 4 \mod{29} \cr}$$

$$\matrix{ m & 7 & 29 \cr p & 29 & 7 \cr s & 1^{-1} = 1 \mod{7} & 7^{-1} = 25 \mod{29} \cr a & 2 & 4 \cr}$$

$$x = 29 \cdot 1 \cdot 2 + 7 \cdot 25 \cdot 4 = 758 = 149 \mod{203}.$$

Hence, $x = -149 = 54 \mod{203}$ is another solution.

Next,

$$\eqalign{ x & = 2 \mod{7} \cr x & = 25 \mod{29} \cr}$$

Note that I don't use $x = 5 \mod{7}$ and $x = 25 \mod{29}$ , because these are are negatives of the solutions I used first, so I'll just get 149 and 54 again.

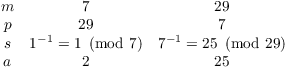
$$\matrix{ m & 7 & 29 \cr p & 29 & 7 \cr s & 1^{-1} = 1 \mod{7} & 7^{-1} = 25 \mod{29} \cr a & 2 & 25 \cr}$$

$$x = 29 \cdot 1 \cdot 2 + 7 \cdot 25 \cdot 25 = 4433 = 170 \mod{203}.$$

Hence, $x = -170 = 33 \mod{203}$ is another solution.

All together, the solutions are $x = 33, 54, 149, 170 \mod{203}$ .

34. Find a solution to $x^2 = 208 \mod{289}$ by lifting a solution to the congruence mod 17.

Consider

$$x^2 = 208 = 4 \mod{17}.$$

Obviously, $x = 2 \mod{17}$ is a solution.

Method 1. Try to find a solution of the form $y = 2 + 17 k$ to the original congruence:

$$\eqalign{ y^2 & = 208 \mod{289} \cr (2 + 17 k)^2 & = 208 \mod{289} \cr 4 + 68 k + 289 k^2 & = 208 \mod{289} \cr 68 k & = 204 \mod{289} \cr 68 k & = 68 \cdot 3 \mod{289} \cr}$$

I cancel the factor of 68, dividing the modulus by $(289, 68) = 17$ . This gives

$$k = 3 \mod{17}.$$

So one solution is obtained by taking $k = 3$ , which gives

$$y = 2 + 17 \cdot 3 = 53 \mod{289}.$$

Method 2. Use the algorithm given by the proof of the theorem on lifting solutions to polynomial congruences.

Let $f'(x) = x^2 - 208$ , so $f'(x) = 2 x$ .

$$f'(2) = 4, \quad f(2) = -204.$$

Note that $17 \notdiv 4$ .

Solve:

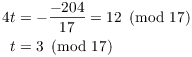
$$\eqalign{ 4 t & = -\dfrac{-204}{17} = 12 \mod{17} \cr t & = 3 \mod{17} \cr}$$

A solution to the original congruence is given by

$$x = 2 + 17 \cdot 3 = 53 \mod{289}.$$

The other solution is $-53 = 236 \mod{289}$ .

35. Suppose that p is an odd prime and $p = 19 \mod{20}$ . Compute $\legendre{-5}{p}$ .

First, $\legendre{-5}{p} = \legendre{-1}{p}\legendre{5}{p}$ .

Since $p = 19 \mod{20}$ , I may write $p = 19 + 20 s$ . Then $p = 3 \mod{4}$ , so $\legendre{-1}{p} = -1$ .

Similarly, $\legendre{5}{p} = \legendre{p}{5}$ . But $p = 19 + 20 s$ shows that $p = 4 \mod{5}$ , so

$$\legendre{p}{5} = \legendre{4}{5} = 1.$$

Therefore, $\legendre{-5}{p} = (-1)(1) = -1$ .

36. Compute $\legendre{180}{211}$ .

$$\legendre{180}{211} = \legendre{5 \cdot 36}{211} = \legendre{5}{211}\legendre{36}{211} = \legendre{5}{211}\cdot 1 = \legendre{5}{211}.$$

Since $5 = 4 \cdot 1 + 1$ ,

$$\legendre{5}{211} = \legendre{211}{5} = \legendre{1}{5} = 1.$$

Therefore, $\legendre{180}{211} = 1$ .

37. Compute $\legendre{375}{461}$ .

I'll use Jacobi symbols to simplify the computation:

$$\legendre{375}{461} = \legendre{25 \cdot 15}{461} = \legendre{15}{461} = \legendre{461}{15} = \legendre{11}{15} =$$

$$\legendre{11}{3} \legendre{11}{5} = \legendre{2}{3} \legendre{1}{5} = (-1)(1) = -1.\quad\halmos$$

38. Convert 2781 to base 5.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 5 & & 2781 & & - & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 5 & & 556 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 5 & & 111 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 5 & & 22 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 5 & & 4 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 5 & & 0 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus, $2781 = (42111)_5$ .

39. Express 0.26 in base 5.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & a & & x & & $b x$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & - & & 0.26 & & 1.3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 0.3 & & 1.5 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 0.5 & & 2.5 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 0.5 & & 2.5 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 0.5 & & 2.5 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus, $0.26 = (0.11222 \ldots)_5 = (0.11\overline{2})_5$ .

40. Find a decimal fraction in lowest terms equal to $(0.2\overline{56})_7$ .

Let $x = (0.2\overline{56})_7$ . Then $49 x = (25.6\overline{56})_7$ , so

$$\eqalign{49 x & = (25.6\overline{56})_7 \cr x & = (0.2\overline{56})_7 \cr \noalign{\vskip2 pt\hrule\vskip2 pt} 48 x & = (25.4)_7 \cr 48 x & = 2 \cdot 7 + 5 + 4 \cdot \dfrac{1}{7} \cr 48 x & = \dfrac{137}{7} \cr x & = \dfrac{137}{336} \quad\halmos \cr}$$

41. Express $(.1\overline{25})_6$ as a decimal fraction in lowest terms.

Let $x = (.1\overline{25})_6$ . Then $36 x = (12.5\overline{25})_6$ , so

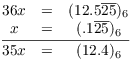
$$\matrix{ 36 x & = & (12.5\overline{25})_6 \cr x & = & (.1\overline{25})_6 \cr \noalign{\vskip2 pt\hrule\vskip2 pt} 35 x & = & (12.4)_6 \cr}$$

Now

$$(12.4)_6 = 1 \cdot 6^1 + 2 \cdot 6^0 + 4 \cdot \dfrac{1}{6} = 8 + \dfrac{2}{3} = \dfrac{26}{3}.$$

Hence,

$$35 x = \dfrac{26}{3}, \quad x = \dfrac{26}{105}.\quad\halmos$$

42. If b is an integer and $b > 1$ , find a decimal fraction equal to $(0.\overline{1})_b$ .

$$(0.\overline{1})_b = \dfrac{1}{b} + \dfrac{1}{b^2} + \dfrac{1}{b^3} + \cdots = \dfrac{1}{b}\cdot \sum_{n=0}^\infty \left(\dfrac{1}{b}\right)^n = \dfrac{1}{b}\cdot \dfrac{1}{1 - \dfrac{1}{b}} = \dfrac{1}{b - 1}.\quad\halmos$$

43. Find the finite continued fraction expansion for $\dfrac{271}{43}$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & a & & q & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 271 & & - & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 43 & & 6 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 13 & & 3 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 4 & & 3 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1 & & 4 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\dfrac{271}{43} = [6; 3, 3, 4] = 6 + \dfrac{1}{3 + \dfrac{1}{3 + \dfrac{1}{4}}}.\quad\halmos$$

44. (a) Find the first 5 convergents of $[7; \overline{5, 10}]$ .

(b) Find the exact value of $x = [7; \overline{5, 10}]$ .

(a)

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & $a_k$ & & $p_k$ & & $q_k$ & & $c_k$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 7 & & 7 & & 1 & & 7 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 5 & & 36 & & 5 & & $\dfrac{36}{5}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 10 & & 367 & & 51 & & $\dfrac{367}{51}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 5 & & 1871 & & 260 & & $\dfrac{1871}{260}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 10 & & 19077 & & 2651 & & $\dfrac{19077}{2651}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

(b)

$$x = 7 + \dfrac{1}{5 + \dfrac{1}{10 + \dfrac{1}{5 + \ddots}}}.$$

Therefore,

$$x - 7 = \dfrac{1}{5 + \dfrac{1}{10 + \dfrac{1}{5 + \ddots}}} = \dfrac{1}{5 + \dfrac{1}{10 + (x - 7)}} = \dfrac{1}{5 + \dfrac{1}{x + 3}} = \dfrac{x + 3}{5 x + 16}.$$

Thus,

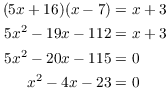
$$\eqalign{(5 x + 16)(x - 7) & = x + 3 \cr 5 x^2 - 19 x - 112 & = x + 3 \cr 5 x^2 - 20 x - 115 & = 0 \cr x^2 - 4 x - 23 & = 0 \cr}$$

This gives the roots

$$x = \dfrac{4 \pm \sqrt{16 + 92}}{2} = 2 \pm 3 \sqrt{3}.$$

Since x is obviously positive, it follows that $x = 2 + 3 \sqrt{3}$ .

45. Find the first 10 terms of the continued fraction expansion of $\root 3 \of {114}$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $x_k$ & & $a_k$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 4.84881 & & 4 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.17812 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 5.61409 & & 5 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.62843 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.59127 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.69128 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.44659 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 2.23921 & & 2 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 4.18051 & & 4 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 5.53997 & & 5 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1.85197 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

46. (a) Find the continued fraction expansion of $\sqrt{7}$ . Find the convergents $c_0$ , ..., $c_8$ .

(b) Use the convergents of the continued fraction expansion of $\sqrt{7}$ to find a solution to the Fermat-Pell equation $x^2 - 7 y^2 = 1$ .

(a) I'll use the recursion formula

$$x_0 = x, \quad a_0 = [x_0],$$

$$x_k = \dfrac{1}{x_{k-1} - a_{k-1}}, \quad a_k = [x_k], \quad k \ge 1.$$

Note that since $\sqrt{7}$ is a quadratic irrational, I can stop once I see that the expansion has repeated.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & x & & a & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\sqrt{7}$ & & 2 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\dfrac{1}{\sqrt{7} - 2} \approx 1.54858$ & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\approx 1.82288$ & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\approx 1.21525$ & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\approx 4.64575$ & & 4 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\approx 1.54858$ & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\approx 1.82288$ & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus, $\sqrt{7} = [2;\overline{1, 1, 1, 4}]$ . The convergents are

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & $a_k$ & & $p_k$ & & $q_k$ & & $c_k$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 3 & & 1 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 5 & & 2 & & $\dfrac{5}{2}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 8 & & 3 & & $\dfrac{8}{3}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 4 & & 37 & & 14 & & $\dfrac{37}{14}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 45 & & 17 & & $\dfrac{45}{17}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 82 & & 31 & & $\dfrac{82}{31}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 127 & & 48 & & $\dfrac{127}{48}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 4 & & 590 & & 223 & & $\dfrac{590}{223}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Note that $\sqrt{7} \approx 2.64575$ , while $\dfrac{590}{223} \approx 2.64574$ .

(b) Since the period is 4, which is even, the numerator $p_3$ and denominator $q_3$ give a solution:

$$8^2 - 7 \cdot 3^2 = 1.\quad\halmos$$

47. Find the convergents of the finite continued fraction $[1; 1, 4, 1, 4, 1, 4]$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & $a_k$ & & $p_k$ & & $q_k$ & & $c_k$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 4 & & 9 & & 5 & & $\dfrac{9}{5}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 11 & & 6 & & $\dfrac{11}{6}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 4 & & 53 & & 29 & & $\dfrac{53}{29}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 64 & & 35 & & $\dfrac{64}{35}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 4 & & 309 & & 169 & & $\dfrac{309}{169}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

48. Find the exact value of the periodic continued fraction $[1; \overline{2, 5}]$ .

Write $x = [1;\overline{2, 5}]$ , so

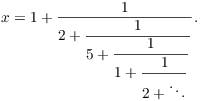
$$x = 1 + \dfrac{1}{2 + \dfrac{1}{5 + \dfrac{1}{1 + \dfrac{1}{2 + \ddots}}}}.$$

Let $y = [\overline{2, 5}]$ , so $x = 1 + \dfrac{1}{y}$ . Then

$$y = 2 + \dfrac{1}{5 + \dfrac{1}{2 + \dfrac{1}{5 + \ddots}}} = 2 + \dfrac{1}{5 + \dfrac{1}{y}} = 2 + \dfrac{1}{\dfrac{5 y + 1}{y}} = 2 + \dfrac{y}{5 y + 1} = \dfrac{2(5 y + 1) + y}{5 y + 1} = \dfrac{11 y + 2}{5 y + 1}.$$

Clear the fraction to obtain a quadratic:

$$5 y^2 + y = 11 y + 2, \quad 5 y^2 - 10 y - 2 = 0.$$

The solutions are

$$y = \dfrac{10 \pm \sqrt{140}}{10}.$$

y must be positive, so

$$y = \dfrac{10 + \sqrt{140}}{10} = \dfrac{10 + 2\sqrt{35}}{10} = \dfrac{5 + \sqrt{35}}{5}.$$

Hence,

$$x = 1 + \dfrac{1}{\dfrac{5 + \sqrt{35}}{5}} = 1 + \dfrac{5}{5 + \sqrt{35}} = \dfrac{10 + \sqrt{35}}{5 + \sqrt{35}} = \dfrac{-3 + \sqrt{35}}{2}.\quad\halmos$$

49. Find the rational number $\dfrac{p}{q}$ in lowest terms with $q \le 50$ which best approximates $\dfrac{\pi}{e}$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & a & & p & & q & & c & & error & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1.15573 & & 1 & & 1 & & 1 & & 1 & & 0.015573 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 6.42148 & & 6 & & 7 & & 6 & & $\dfrac{7}{6}$ & & 0.01094 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2.37259 & & 2 & & 15 & & 13 & & $\dfrac{15}{13}$ & & 0.00188 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2.68389 & & 2 & & 37 & & 32 & & $\dfrac{37}{32}$ & & 0.00052 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1.46223 & & 1 & & 52 & & 45 & & $\dfrac{52}{45}$ & & 0.00017 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2.16342 & & 2 & & 141 & & 122 & & $\dfrac{141}{122}$ & & 0.00001 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

I computed the first six convergents for the continued fraction expansion for $\dfrac{\pi}{e}$ . I conjecture that $\dfrac{52}{45}$ is the best rational approximation with denominator less than or equal to 50.

Suppose that $\dfrac{p}{q}$ is a better approximation, and $q \le 50$ . Then

$$\left|\dfrac{\pi}{e} - \dfrac{p}{q}\right| < \left|\dfrac{\pi}{e} - \dfrac{52}{45}\right| \approx 0.00017.$$

Now $q \le 50$ , so

$$\dfrac{1}{2 q^2} \ge \dfrac{1}{5000} = 0.0002.$$

Hence,

$$\dfrac{1}{2 q^2} > \left|\dfrac{\pi}{e} - \dfrac{p}{q}\right|.$$

Therefore, $\dfrac{p}{q}$ must be a convergent. However, the table shows that no convergent with denominator less than or equal to 50 approximates $\dfrac{\pi}{e}$ better than $\dfrac{52}{45}$ . Hence, there is no such $\dfrac{p}{q}$ , and $\dfrac{52}{45}$ is the best rational approximation with denominator less than or equal to 50.

The best thing for being sad is to learn something. - Merlyn, in T.H. White's The Once and Future King

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga