Review Problems for Test 1

Math 393

These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the absence of a topic does not imply that it won't appear on the test.

1. Consider the set of integers

$$S = \left\{n \mid 10 n \ge n^2 + 21\right\}.$$

When the Well-Ordering Axiom is applied to S, it asserts the existence of a certain element of S. What is the element?

2. (a) Let S be the set of real numbers x such that $x > 3$ , with the usual ordering. Is S well-ordered?

(b) Let S be the set of integers x such that $x > 3$ , with the usual ordering. Is S well-ordered?

3. Compute $[3.2]$ , $[-5.53]$ , and $\left[\dfrac{100}{7}\right]$ .

4. Compute the exact value of $\displaystyle \sum_{n = 1}^{50} \ln \dfrac{n + 1}{n}$ .

5. Compute the exact value of $\displaystyle \prod_{n = 1}^{50} \left(1 + \dfrac{3}{n} + \dfrac{3}{n^2} + \dfrac{1}{n^3}\right)$ .

6. Simplify $\displaystyle {{31} \choose {17}} + {{31} \choose {18}}$ to a single binomial coefficient.

7. The Gamma function is defined by

$$\Gamma(x) = \int_0^\infty e^{-t} t^{x - 1}\,dt.$$

Prove that if $x > 0$ , then

$$\Gamma(x + 1) = x \Gamma(x).$$

Thus, the Gamma function satisfies the same kind of recursion relation as the factorial function.

8. Prove that if $n \ge 0$ and $0 \le k \le n$ , then

$$n {n \choose k} = (k + 1) {n \choose {k + 1}} + k {n \choose k}.$$

9. Find the coefficient of $x^{11}y^{15}$ in the expansion of $(2 x - y^3)^{16}$ .

10. Find $(3914, 2442)$ and express it as a linear combination of 3914 and 2442.

11. Calvin Butterball has two egg timers that he bought after watching an ad on TV. One timer rings exactly 8 minutes after it is started; the other rings exactly 15 minutes after it is started. While each timer is running, no information about the time it is keeping is available. How can Calvin use the timers to time a 4-minute egg?

12. Find the greatest common divisor and least common multiple of $2^3 \cdot 3^{10} \cdot 5^6 \cdot 13^4$ and $2 \cdot 3^8 \cdot 5^3 \cdot 7^3 \cdot 11 \cdot 13^2$ .

13. The sum of two numbers is 2736. Their least common multiple is 77592. Find the numbers.

Note: This is a difficult problem; try it last, and if you get stuck, at least try to follow the solution.

14. (a) If x is an integer, can $(x + 5)(x + 4)$ be prime?

(b) If x is a positive integer, can $(x + 5)(x + 4)$ be prime?

(c) If x is an integer, can $x^2 + 2$ be prime?

15. Prove that if n is an integer and $n \ge 1$ , then $15^n + 5^n + 3^n + 1$ is not prime.

16. Prove that if $n \in \integer$ leaves a remainder of 4 when it's divided by 5, then $n^2 + n + 3$ leaves a remainder of 3 when it's divided by 5.

17. Prove that the square of an integer does not leave a remainder of 2 when it's divided by 3.

18. Give three integers a, b, and c such that a does not divide either b or c, but a divides $b + c$ .

19. Let c, x, and y be integers, where $c \ne 0$ . Prove that $x \mid y$ if and only if $c x \mid c y$ .

20. Calvin Butterball reasons that if $a, b \in \integer$ , then $\dfrac{a}{(a, b)}$ and b must be relatively prime, because you've divided out of a all the factors that a and b had in common.

If he's right, prove it. If he's wrong, give a specific counterexample.

21. Suppose $n \in \integer$ . What are the possible values of $(n + 4, (n + 2)^2)$ ?

22. Let n be a positive integer, and let x be an integer. Suppose that $n \mid 3 x + 1$ and $n \mid 6 x^2 + 2 x + 1$ . Prove that $n = 1$ .

23. Prove that if $n \in \integer^+$ and $n + 1 \mid n^2 + 1$ , then $n = 1$ .

24. How many integers in the set $\{1, 2, 3, \ldots, 5000\}$ are by either 3 or 7, but not by both?

25. How many integers in the set $\{1, 2, 3, \ldots, 5000\}$ are divisible by 3 but not 7?

26. Prove that if $a, b, n \in \integer$ and n divides both $3 a + 2 b$ and $4 a + 3 b$ , then $n \mid a$ .

27. Suppose that m and n are integers, and you know that

$$a m + b n = 35 \quad\hbox{for some}\quad a, b \in \integer.$$

What are the possible values of $(m, n)$ ? Why?

28. Prove that if n is a positive integer of the form $4 k + 3$ , then n must have a prime factor of that form.

29. Prove that if $n \ge 1$ , then

$$1 \cdot 2^1 + 2 \cdot 2^2 + 3 \cdot 2^3 + \cdots + n \cdot 2^n = 2 + (n - 1) 2^{n + 1}.$$

30. Prove that if $f_n$ denotes the $n^{\rm th}$ Fibonacci number (where $f_0 = 1$ and $f_1 = 1$ ), then

$$f_{n - 1} + 2 f_n + f_{n + 1} = f_{n + 3} \quad\hbox{for}\quad n \ge 1.$$

31. Let $f_n$ denote the $n^{\rm th}$ Fibonacci number (where $f_0 = 1$ and $f_1 = 1$ ).

Prove that if $n \ge 1$ , then

$$\left[\matrix{1 & 1 \cr 1 & 0 \cr}\right]^{n + 1} = \left[\matrix{f_{n + 1} & f_n \cr f_n & f_{n - 1} \cr}\right].$$

32. A sequence of integers is defined by

$$x_0 = 5, \quad x_1 = 7,$$

$$x_n = x_{n - 1} + 20 x_{n-2} \quad\hbox{for}\quad n \ge 2.$$

Prove that

$$x_n = 3 \cdot 5^n + 2 \cdot (-4)^n \quad\hbox{for}\quad n \ge 0.$$

33. Use induction to prove that $n! > 3^n$ for $n \ge 7$ .

34. Let $n \in \integer^+$ . Prove that

$$9 \mid 10^n + 3 \cdot 4^{n + 2} + 5.$$

35. Let $f(x)$ be a polynomial with integer coefficients, and let $f'(x)$ be the derivative. Prove that

$$f(x + 3) = f(x) + 3 f'(x) \mod{9}.$$

Hint: Use induction on the degree of f. For the induction step, write

$$f(x) = a_0 + a_1 x + \cdots + a^n x^n + a_{n + 1} x^{n + 1} = a_0 + x (a_1 + \cdots + a^n x^{n - 1} + a_{n + 1} x^n).$$

Let $g(x) = a_1 + \cdots + a^n x^{n - 1} + a_{n + 1} x^n$ and apply the induction hypothesis to $g(x)$ .

36. Let x, y, and z be positive integers, and suppose the products $xy$ , $yz$ , and $xz$ are all perfect cubes. Prove that x, y, and z must be perfect cubes.

37. Suppose that p, q, and r are distinct prime numbers,

$$x = p q^2 r^4, \quad y = p^a q^b, \quad\hbox{and}\quad y \mid x.$$

What are the possible values of y?

38. Suppose that the prime factorization of an integer n is

$$n = p_1^3 \cdot p_2^6 \cdot p_3^5.$$

($p_1$ , $p_2$ , and $p_3$ are distinct primes.)

Write n as a product of integers $n = a b$ , where a is a perfect square and b is square-free --- that is, b is not divisible by the square of any positive integer except 1.

39. Find the prime factorization of 15400 by trial division.

40. Use Fermat factorization to factor 25877 into primes. (You should use Fermat factorization rather than some other method, and you should show the trial values.)

41. Find the general solution to the Diophantine equation

$$6 x + 4 y = 10.$$

42. Find the general solution to the Diophantine equation

$$7 x + 23 y = 18.$$

43. Find the general solution to the Diophantine equation

$$6 x - 9 y + 15 z = 21.$$

44. Bonzo buys some books that cost $7 each and some books that cost $15 each. The books cost a total of $349. What is the largest total number of books Bonzo could have bought?

45. I. M. Snarky buys 43 apples and oranges. The apples cost 10 cents more than the oranges, and he spends a total of $30.68. Find the number of each fruit that he bought and their prices.

46. Solve the following Diophantine equation by factoring:

$$x^2 = 7 + 4 y^2.$$

47. Is $4 \cdot 3^{1000} + 7^{1000}$ prime?

48. Find $52^{-1} \mod{77}$ .

49. Suppose that $(m, n) = 1$ . Prove that if $a = b \mod{m}$ and $a = b \mod{n}$ , then $a = b \mod{m n}$ .

50. Prove that if $n \in \integer$ , then $n^3 + 4 n + 2$ is not divisible by 5.

51. (a) Construct a table for multiplication mod 8.

(b) What is the multiplicative inverse of 5 mod 8?

52. Prove by contradiction that 15 does not have a multiplicative inverse mod 42.

53. Prove that if n is a positive integer, then

$$7^n = 6 n + 1 \mod{36}.$$

54. By constructing a table, show that $x^2 + 3 x + 2 = 0 \mod{6}$ has 4 solutions mod 6. (Note that quadratics "usually" have at most two roots!)

55. (a) Prove that the sum of the cubes of two integers does not leave a remainder of 4 when the sum is divided by 7.

(b) Prove that the Diophantine equation $x^3 + y^3 = 4$ has no solutions.

Solutions to the Review Problems for Test 1

1. Consider the set of integers

$$S = \left\{n \mid 10 n \ge n^2 + 21\right\}.$$

When the Well-Ordering Axiom is applied to S, it asserts the existence of a certain element of S. What is the element?

First

$$\eqalign{ 10 n & \ge n^2 + 21 \cr 0 & \ge n^2 - 10 n + 21 \cr 0 & \ge (n - 3)(n - 7) \cr}$$

The integers which satisfy this inequality are 3, 4, 5, 6, and 7.

Well-Ordering says that a nonempty subset of the positive integers has a smallest element. The smallest element of S is 3.

2. (a) Let S be the set of real numbers x such that $x > 3$ , with the usual ordering. Is S well-ordered?

(b) Let S be the set of integers x such that $x > 3$ , with the usual ordering. Is S well-ordered?

(a) S is not well-ordered, because S has subsets which do not have smallest elements. For example, S itself does not have a smallest element (note that $3 \notin S$ ).

(b) S is well-ordered. In fact, it is just $\{4, 5, 6, \ldots \}$ , which is the set of positive integers translated 3 units to the right. Since the set of positive integers is well-ordered, S is as well.

3. Compute $[3.2]$ , $[-5.53]$ , and $\left[\dfrac{100}{7}\right]$ .

$$[3.2] = 3, \quad [-5.53] = -6, \quad \left[\dfrac{100}{7}\right] = 14.\quad\halmos$$

4. Compute the exact value of $\displaystyle \sum_{n = 1}^{50} \ln \dfrac{n + 1}{n}$ .

Note that

$$\ln \dfrac{n + 1}{n} = \ln (n + 1) - \ln n.$$

So

$$\sum_{n = 1}^{50} \ln \dfrac{n + 1}{n} = \sum_{n = 1}^{50} \left(\ln (n + 1) - \ln n\right).$$

Write out some terms of the sum:

$$\eqalign{ \left(\ln 2 - \ln 1\right) + \cr \left(\ln 3 - \ln 2\right) + \cr \left(\ln 4 - \ln 3\right) + \cr \vdots \cr \left(\ln 50 - \ln 49\right) + \cr \left(\ln 51 - \ln 50\right) \cr}$$

Almost all the terms cancel in pairs, with a negative term cancelling with the positive term in the following expression. The remaining terms give the value of he sum:

$$\sum_{n = 1}^{50} \ln \dfrac{n + 1}{n} = \ln 51 - \ln 1 = \ln 51.\quad\halmos$$

5. Compute the exact value of $\displaystyle \prod_{n = 1}^{50} \left(1 + \dfrac{3}{n} + \dfrac{3}{n^2} + \dfrac{1}{n^3}\right)$ .

Note that

$$1 + \dfrac{3}{n} + \dfrac{3}{n^2} + \dfrac{1}{n^3} = \dfrac{n^3 + 3 n^2 + 3 n + 1}{n^3} = \dfrac{(n + 1)^3}{n^3}.$$

So

$$\prod_{n = 1}^{50} \left(1 + \dfrac{3}{n} + \dfrac{3}{n^2} + \dfrac{1}{n^3}\right) = \prod_{n = 1}^{50} \dfrac{(n + 1)^3}{n^3}.$$

Write out some terms of the product:

$$\dfrac{2^3}{1^3} \cdot \dfrac{3^3}{2^3} \cdot \dfrac{4^3}{3^3} \cdot \cdots \cdot \dfrac{50^3}{49^3} \cdot \dfrac{51^3}{50^3}.$$

Most of the terms in the numerators cancel with terms in the denominators. The remaining terms give the value of the product:

$$\prod_{n = 1}^{50} \left(1 + \dfrac{3}{n} + \dfrac{3}{n^2} + \dfrac{1}{n^3}\right) = \dfrac{51^3}{1^3} = 132651.\quad\halmos$$

6. Simplify $\displaystyle {{31} \choose {17}} + {{31} \choose {18}}$ to a single binomial coefficient.

Use the formula

$${n \choose k} + {n \choose {k + 1}} = {{n + 1} \choose {k + 1}}.$$

Put $n = 31$ and $k = 17$ . Thus,

$${{31} \choose {17}} + {{31} \choose {18}} = {{32} \choose {18}}.\quad\halmos$$

7. The Gamma function is defined by

$$\Gamma(x) = \int_0^\infty e^{-t} t^{x - 1}\,dt.$$

Prove that if $x > 0$ , then

$$\Gamma(x + 1) = x \Gamma(x).$$

Thus, the Gamma function satisfies the same kind of recursion relation as the factorial function.

$$\Gamma(x + 1) = \int_0^\infty e^{-t} t^x\,dt.$$

Integrate $\Gamma(x + 1)$ by parts:

$$\matrix{ & \displaystyle \der {} t & \displaystyle \int\,dt \cr \noalign{\vskip2 pt} + & t^x & e^{-t} \cr \noalign{\vskip2 pt} - & x t^{x - 1} & -e^{-t} \cr}$$

Then

$$\Gamma(x + 1) = \left[-t^x e^{-t} + \int x e^{-t} t^{x - 1}\,dt\right]_0^\infty.$$

The first term $-t^x e^{-t}$ is 0 when $t = 0$ and approaches 0 as $t \to \infty$ . Therefore, the last equation becomes

$$\Gamma(x + 1) = \int_0^\infty x e^{-t} t^{x - 1}\,dt = x \Gamma(x).\quad\halmos$$

8. Prove that if $n \ge 0$ and $0 \le k \le n$ , then

$$n {n \choose k} = (k + 1) {n \choose {k + 1}} + k {n \choose k}.$$

I'll expand the right side as factorials and combine the fractions over a common denominator:

$$(k + 1) {n \choose {k + 1}} + k {n \choose k} = (k + 1) \dfrac{n!}{(k + 1)!\, (n - k - 1)!} + k \dfrac{n!}{k!\, (n - k)!} = \dfrac{n!}{k!\, (n - k - 1)!} + \dfrac{k \cdot n!}{k!\, (n - k)!} =$$

$$\dfrac{n!}{k!\, (n - k - 1)!} \cdot \dfrac{n - k}{n - k} + \dfrac{k \cdot n!}{k!\, (n - k)!} = \dfrac{(n - k) n! + k n!}{k!\, (n - k)!} = \dfrac{(n - k + k) n!}{k!\, (n - k)!} = \dfrac{n n!}{k!\, (n - k)!} = n {n \choose k}.\quad\halmos$$

9. Find the coefficient of $x^{11}y^{15}$ in the expansion of $(2 x - y^3)^{16}$ .

$x^{11}y^{15}$ occurs in the term $(2 x)^{11}(-y^3)^5$ . The full term is

$${{16} \choose {11}}(2 x)^{11}(-y^3)^5 = -{{16} \choose {11}}\cdot 2^{11}x^{11}y^{15}.$$

The coefficient is $-{{16} \choose {11}}\cdot 2^{11} = -8945664$ .

10. Find $(3914, 2442)$ and express it as a linear combination of 3914 and 2442.

Use the Extended Euclidean Algorithm:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 3914 & & - & & 460 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2442 & & 1 & & 287 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1472 & & 1 & & 173 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 970 & & 1 & & 114 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 502 & & 1 & & 59 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 468 & & 1 & & 55 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 34 & & 13 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 26 & & 1 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 8 & & 3 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 4 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Therefore,

$$(3914, 2442) = 2 = (-287)(3914) + (460)(2442).\quad\halmos$$

11. Calvin Butterball has two egg timers that he bought after watching an ad on TV. One timer rings exactly 8 minutes after it is started; the other rings exactly 15 minutes after it is started. While each timer is running, no information about the time it is keeping is available. How can Calvin use the timers to time a 4-minute egg?

$(8, 15) = 1$ , and in fact,

$$1 = 2 \cdot 8 + (-1) \cdot 15.$$

Multiply by 4:

$$4 = 8 \cdot 8 + (-4) \cdot 15.$$

According to this equation, Calvin can do the following. Start both timers, restarting each timer when it rings. After the 15-minute timer has cycled 4 times, start cooking the egg. Stop cooking the egg when the 8-minute timer has cycled 8 times.

In the same way, Calvin can use the two timers to time any integral number of minutes.

12. Find the greatest common divisor and least common multiple of $2^3 \cdot 3^{10} \cdot 5^6 \cdot 13^4$ and $2 \cdot 3^8 \cdot 5^3 \cdot 7^3 \cdot 11 \cdot 13^2$ .

For the greatest common divisor, take the smallest power of each prime power the numbers have in common:

$$(2^3 \cdot 3^{10}\cdot 5^6 \cdot 13^4, 2 \cdot 3^8 \cdot 5^3 \cdot 7^3 \cdot 11 \cdot 13^2) = 2 \cdot 3^8 \cdot 5^3 \cdot 13^2.$$

For the least common multiple, take the largest power of each prime power contained in either number:

$$[2^3 \cdot 3^{10}\cdot 5^6 \cdot 13^4, 2 \cdot 3^8 \cdot 5^3 \cdot 7^3 \cdot 11 \cdot 13^2] = 2^3 \cdot 3^{10}\cdot 5^6 \cdot 7^3 \cdot 11 \cdot 13^4.\quad\halmos$$

13. The sum of two numbers is 2736. Their least common multiple is 77592. Find the numbers.

Suppose m and n are the numbers, so

$$m + n = 2736 \quad\hbox{and}\quad [m, n] = 77592.$$

Let p be a prime number that goes into both 2736 and 77592. Since 77592 is a multiple of m and of n, p must divide at least one of m and n.

If $p \mid m$ , then since $p \mid m + n = 2736$ , I have $p \mid (m + n) - m = n$ .

Similarly, if $p \mid n$ , then since $p \mid m + n = 2736$ , I have $p \mid (m + m) - n = m$ .

In other words, any prime factor of both 2736 and 77592 must be a prime factor of both m and n.

It also goes the other way: If a prime p divides both m and n, then p clearly divides their least common multiple, as well as $m + n$ by a divisibility property.

Hence, the greatest common divisor of 2736 and 77592 is the same as the greatest common divisor of m and n.

By the Euclidean algorithm, $(2736, 77592) = 24$ . So I have

$$\eqalign{ m + n & = 2736 \cr \dfrac{m}{24} + \dfrac{n}{24} & = 114 \cr}$$

Note that, since 24 divides both m and n, the two fractions in the last equation are actually integers.

If I divide 24 out of both m and n, then 24 is divided out of their least common multiple. So

$$\left[\dfrac{m}{24}, \dfrac{n}{24}\right] = \dfrac{77592}{24} = 3233.$$

Since 24 was the greatest common divisor of m and n, the numbers $\dfrac{m}{24}$ and $\dfrac{n}{24}$ are relatively prime. Hence, their least common multiple is their product:

$$\eqalign{ \left[\dfrac{m}{24}, \dfrac{n}{24}\right] & = 3233 \cr \dfrac{m}{24} \cdot \dfrac{n}{24} & = 3233 \cr m n & = 1862208 \cr}$$

Then $m = \dfrac{1862208}{n}$ , so

$$\eqalign{ m + n & = 2736 \cr \dfrac{1862208}{n} + n & = 2736 \cr 1862208 + n^2 & = 2736 n \cr n^2 - 2736 n + 1862208 & = 0 \cr}$$

You can solve this ugly quadratic using the Quadratic Formula; the roots are 1272 and 1464. Either root gives the pair of numbers $\{1272, 1464\}$ , and they are the solution to the problem.

14. (a) If x is an integer, can $(x + 5)(x + 4)$ be prime?

(b) If x is a positive integer, can $(x + 5)(x + 4)$ be prime?

(c) If x is an integer, can $x^2 + 2$ be prime?

(a) Yes. If $x = -3$ , then $(x + 5)(x + 4) = 2 \cdot 1 = 2$ , which is prime.

(b) No. If $x > 0$ , then $x + 5 > 5$ and $x + 4 > 4$ , so $(x + 5)(x + 4)$ is a proper factorization (neither factor is equal to 1). Therefore, $(x + 5)(x + 4)$ cannot be prime.

(c) Yes. If $x = 3$ , then $x^2 + 2 = 11$ , which is prime.

(Don't make the mistake of thinking that since $x^2 + 2$ "doesn't factor" as a polynomial over $\real$ , that its values must always be composite.

15. Prove that if n is an integer and $n \ge 1$ , then $15^n + 5^n + 3^n + 1$ is not prime.

Note that

$$15^n + 5^n + 3^n + 1 = (5^n + 1)(3^n + 1).$$

Since $n \ge 1$ , both factors $5^n + 1$ and $3^n + 1$ are greater than 1. Hence, this is a proper factorization, and $15^n + 5^n + 3^n + 1$ is not prime.

16. Prove that if $n \in \integer$ leaves a remainder of 4 when it's divided by 5, then $n^2 + n + 3$ leaves a remainder of 3 when it's divided by 5.

Suppose that $n \in \integer$ leaves a remainder of 4 when it's divided by 5. Then $n = 5 k + 4$ for $k \in \integer$ . So

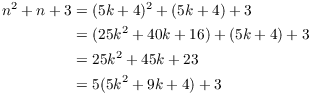
$$\eqalign{ n^2 + n + 3 & = (5 k + 4)^2 + (5 k + 4) + 3 \cr & = (25 k^2 + 40 k + 16) + (5 k + 4) + 3 \cr & = 25 k^2 + 45 k + 23 \cr & = 5(5 k^2 + 9 k + 4) + 3 \cr}$$

This shows that $n^2 + n + 3$ leaves a remainder of 3 when it's divided by 5.

Note: You can do this with less effort using modular arithmetic.

17. Prove that the square of an integer does not leave a remainder of 2 when it's divided by 3.

Let $n \in \integer$ . By the Division Algorithm, if n is divided by 3, there are 3 possibilities:

$$n = 3 q + 0, \quad n = 3 q + 1, \quad\hbox{and}\quad n = 3 q + 2.$$

I'll consider the cases.

(a) $n = 3 q$ .

$$\eqalign{ n^2 & = (3 q)^2 \cr & = 9 q^2 \cr & = 3(3 q^2) \cr}$$

In this case, $n^2$ leaves a remainder of 0 when it's divided by 3.

(b) $n = 3 q + 1$ .

$$\eqalign{ n^2 & = (3 q + 1)^2 \cr & = 9 q^2 + 6 q + 1\cr & = 3(3 q^2 + 2 q) + 1 \cr}$$

In this case, $n^2$ leaves a remainder of 1 when it's divided by 3.

(b) $n = 3 q + 2$ .

$$\eqalign{ n^2 & = (3 q + 2)^2 \cr & = 9 q^2 + 12 q + 4\cr & = 3(3 q^2 + 4 q + 1) + 1 \cr}$$

In this case, $n^2$ leaves a remainder of 1 when it's divided by 3.

Therefore, the square of an integer never leaves a remainder of 2 when it's divided by 3.

Note: You can do this with less effort using modular arithmetic. Just construct a tables of squares mod 3:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & n & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & $n^2 \mod{3}$ & & 0 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

18. Give three integers a, b, and c such that a does not divide either b or c, but a divides $b + c$ .

For instance, $3 \notdiv 5$ and $3 \notdiv 7$ , but $3 \mid 5 + 7 = 12$ .

It is true that if a divides b and a divides c, then a divides $b + c$ .

19. Let c, x, and y be integers, where $c \ne 0$ . Prove that $x \mid y$ if and only if $c x \mid c y$ .

Suppose $x \mid y$ . Then $k x = y$ for some k. Hence, $k c x = c y$ . Therefore, $c x \mid c y$ .

Conversely, suppose $c x \mid c y$ . Then $k c x = c y$ for some k. Since $c \ne 0$ , the Zero Divisor Axiom for the integers allows me to cancel c from both sides: $k x = y$ . This implies that $x \mid y$ , which completes the proof.

20. Calvin Butterball reasons that if $a, b \in \integer$ , then $\dfrac{a}{(a, b)}$ and b must be relatively prime, because you've divided out of a all the factors that a and b had in common.

If he's right, prove it. If he's wrong, give a specific counterexample.

Take $a = 8$ and $b = 12$ . Then $(a, b) = 4$ , so

$$\dfrac{a}{(a, b)} = \dfrac{8}{4} = 2.$$

But $\dfrac{a}{(a, b)} = 2$ and $b = 12$ aren't relatively prime. Hence, Calvin is mistaken.

21. Suppose $n \in \integer$ . What are the possible values of $(n + 4, (n + 2)^2)$ ?

I have

$$(n + 4, (n + 2)^2) = (n + 4, n^2 + 4 n + 4) = (n + 4, (n^2 + 4 n + 4) - n(n + 4)) = (n + 4, 4) \mid 4.$$

The positive divisors of 4 are 1, 2, and 4, so the only possibilities are 1, 2, and 4.

If $n = 1$ , then $(n + 4, (n + 2)^2) = (5, 9) = 1$ .

If $n = 2$ , then $(n + 4, (n + 2)^2) = (6, 16) = 2$ .

If $n = 4$ , then $(n + 4, (n + 2)^2) = (8, 36) = 4$ .

Thus, all three possibilities do occur.

22. Let n be a positive integer, and let x be an integer. Suppose that $n \mid 3 x + 1$ and $n \mid 6 x^2 + 2 x + 1$ . Prove that $n = 1$ .

I have

$$n \mid (6 x^2 + 2 x + 1) - (2 x)(3 x + 1) = (6 x^2 + 2 x + 1) - (6 x^2 + 2 x) = 1.$$

Since n is a positive integer, I must have $n = 1$ .

23. Prove that if $n \in \integer^+$ and $n + 1 \mid n^2 + 1$ , then $n = 1$ .

I have

$$n + 1 \mid n^2 + 1 = n^2 + 2 n + 1 - 2 n = (n + 1)^2 - 2 n = (n + 1)^2 - 2(n + 1) + 2.$$

Since $n + 1 \mid (n + 1)^2 - 2(n + 1)$ , I must have $n + 1 \mid 2$ . Thus, $n + 1 = 1$ (and $n = 0$ ) or $n + 1 = 2$ (and $n = 1$ ). Since $n > 0$ , the first case is ruled out, so $n = 1$ .

24. How many integers in the set $\{1, 2, 3, \ldots, 5000\}$ are divisible by either 3 or 7, but not by both?

$$\hbox{\epsfysize=1.5in \epsffile{rev1-1.eps}}$$

There are $\left[\dfrac{5000}{3}\right] = 1666$ integers in $\{1, 2, 3, \ldots, 5000\}$ which are divisible by 3.

There are $\left[\dfrac{5000}{7}\right] = 714$ integers in $\{1, 2, 3, \ldots, 5000\}$ which are divisible by 7.

The integers divisible by both 3 and 7 are the integers divisible by $3 \cdot 7 = 21$ . There are $\left[\dfrac{5000}{21}\right] = 238$ of those. These are counted twice: Among the integers divisible by 3, and among the integers divisible by 7.

Therefore, the number of integers in $\{1, 2, 3, \ldots, 5000\}$ which are divisible by either 3 or 7, but not by both is

$$1666 + 714 - 2 \cdot 238 = 1904.\quad\halmos$$

25. How many integers in the set $\{1, 2, 3, \ldots, 5000\}$ are divisible by 3 but not 7?

$$\hbox{\epsfysize=1.5in \epsffile{rev1-2.eps}}$$

There are $\left[\dfrac{5000}{3}\right] = 1666$ integers in $\{1, 2, 3, \ldots, 5000\}$ which are divisible by 3.

The integers divisible by both 3 and 7 are the integers divisible by $3 \cdot 7 = 21$ . There are $\left[\dfrac{5000}{21}\right] = 238$ of those.

Therefore, the number of integers in $\{1, 2, 3, \ldots, 5000\}$ which are divisible by 3 but not by 7 is

$$1666 - 238 = 1428.\quad\halmos$$

26. Prove that if $a, b, n \in \integer$ and n divides both $3 a + 2 b$ and $4 a + 3 b$ , then $n \mid a$ .

Since $n \mid 3 a + 2 b$ and $n \mid 4 a + 3 b$ , I have

$$n \mid 3(3 a + 2 b) - 2(4 a + 3 b) = a.\quad\halmos$$

27. Suppose that m and n are integers, and you know that

$$a m + b n = 35 \quad\hbox{for some}\quad a, b \in \integer.$$

What are the possible values of $(m, n)$ ? Why?

The greatest common divisor of two numbers divides each of the numbers. Therefore, $(m, n) \mid m$ and $(m, n ) \mid n$ . By divisibility properties, $(m, n)$ divides any linear combination of m and n. Hence,

$$(m, n) \mid a m + b n = 35.$$

Thus, $(m, n)$ is a positive integer that divides 35. The only positive integers that divide 35 are 1, 5, 7, and 35. Thus, $(m, n)$ must be one of these --- but are all of these possible?

I can show that all of these values are possible by finding, for each case, specific values of a, b, m, and n for which $a m + b n = 35$ , and for which $(m, n)$ is the desired number. I'll do this by choosing m and n to give the desired number first, then choosing a and b to get the linear combination to equal 35.

Take $m = 1$ and $n = 1$ , so $(m, n) = 1$ . Then taking $a = 35$ and $b = 0$ , I also have $a m + b n = 34 + 1 = 35$ .

Take $m = 5$ and $n = 5$ , so $(m, n) = 5$ . Then taking $a = 7$ and $b = 0$ , I also have $a m + b n = 35 + 0 = 35$ .

Take $m = 7$ and $n = 7$ , so $(m, n) = 7$ . Then taking $a = 5$ and $b = 0$ , I also have $a m + b n = 35 + 0 = 35$ .

Take $m = 35$ and $n = 35$ , so $(m, n) = 35$ . Then taking $a = 1$ and $b = 0$ , I also have $a m + b n = 35 + 0 = 35$ .

Thus, if $a m + b n = 35$ , then $(m, n)$ is 1, 5, 7, or 35, and all four of these values are possible.

28. Prove that if n is a positive integer of the form $4 k + 3$ , then n must have a prime factor of that form.

By the Division Algorithm, every integer may be divided by 4 leaving a remainder of 0, 1, 2, or 3. Therefore, every integer is equal to $4 k$ , $4 k + 1$ , $4 k + 2$ , or $4 k + 3$ for some k.

Note also that an odd prime number can't have the form $4 k$ or $4 k + 2$ : Numbers of these forms are divisible by 2.

Consider $n = 4 k + 3$ . Factor n into a product of primes. $4 k + 3$ is odd, since it's an even number ($4 k$ ) plus an odd number (3). So n must be a product of odd primes.

These odd primes are either of the form $4 k + 1$ or the form $4 k + 3$ . Could all of them have the form $4 k + 1$ ?

Notice that the product of two numbers of the form $4 k + 1$ is a number of the form $4 k + 1$ :

$$(4 a + 1)(4 b + 1) = 16 ab + 4 a + 4 b + 1 = 4(4 ab + a + b) + 1.$$

If all the prime factors of n have the form $4 k + 1$ , then by induction n has the form $4 k + 1$ as well. This contradicts the fact that $n = 4 k + 3$ .

Therefore, at least one prime factor of n has the form $4 k + 3$ , which is what I wanted to prove.

29. Prove that if $n \ge 1$ , then

$$1 \cdot 2^1 + 2 \cdot 2^2 + 3 \cdot 2^3 + \cdots + n \cdot 2^n = 2 + (n - 1)2^{n + 1}.$$

For $n = 1$ , I have

$$1 \cdot 2^1 = 1 \quad\hbox{and}\quad 2 + (1 - 1)2^{1+1} = 2.$$

The result holds for $n = 1$ .

Suppose that the result is true for n:

$$1 \cdot 2^1 + 2 \cdot 2^2 + 3 \cdot 2^3 + \cdots + n \cdot 2^n = 2 + (n - 1)2^{n + 1}.$$

I must prove the result for $n + 1$ :

$$1 \cdot 2^1 + 2 \cdot 2^2 + 3 \cdot 2^3 + \cdots + n \cdot 2^n + (n + 1) \cdot 2^{n + 1} = 2 + [(n + 1) - 1]2^{(n+1)+1} = 2 + n \cdot 2^{n + 2}.$$

I have

$$1 \cdot 2^1 + 2 \cdot 2^2 + 3 \cdot 2^3 + \cdots + n \cdot 2^n + (n + 1) \cdot 2^{n + 1} = 2 + (n - 1) 2^{n + 1} + (n + 1) \cdot 2^{n + 1} = 2 + [(n - 1) + (n + 1)] 2^{n + 1} =$$

$$2 + 2 n \cdot 2^{n + 1} = 2 + n \cdot 2^{n + 2}.$$

Therefore, the result is true for all $n \ge 1$ by induction.

30. Prove that if $f_n$ denotes the $n^{\rm th}$ Fibonacci number (where $f_0 = 1$ and $f_1 = 1$ ), then

$$f_{n - 1} + 2 f_n + f_{n + 1} = f_{n + 3} \quad\hbox{for}\quad n \ge 1.$$

$$\eqalign{ f_{n - 1} + 2 f_n + f_{n + 1} & = f_{n - 1} + f_n + f_n + f_{n + 1} \cr & = f_{n + 1} + f_{n + 2} \cr & = f_{n + 3} \quad\halmos \cr}$$

31. Let $f_n$ denote the $n^{\rm th}$ Fibonacci number (where $f_0 = 1$ and $f_1 = 1$ ).

Prove that if $n \ge 1$ , then

$$\left[\matrix{1 & 1 \cr 1 & 0 \cr}\right]^{n + 1} = \left[\matrix{f_{n + 1} & f_n \cr f_n & f_{n - 1} \cr}\right].$$

For $n = 1$ , I have

$$\left[\matrix{1 & 1 \cr 1 & 0 \cr}\right]^2 = \left[\matrix{2 & 1 \cr 1 & 1 \cr}\right] \quad\hbox{and}\quad \left[\matrix{f_{1+1} & f_1 \cr f_1 & f_{1-1} \cr}\right] = \left[\matrix{2 & 1 \cr 1 & 1 \cr}\right].$$

Thus, the result is true for $n = 1$ .

Assume that the result is true for n:

$$\left[\matrix{1 & 1 \cr 1 & 0 \cr}\right]^{n + 1} = \left[\matrix{f_{n + 1} & f_n \cr f_n & f_{n - 1} \cr}\right].$$

I must prove the result for $n + 1$ :

$$\left[\matrix{1 & 1 \cr 1 & 0 \cr}\right]^{n + 2} = \left[\matrix{f_{n + 2} & f_{n + 1} \cr f_{n + 1} & f_n \cr}\right].$$

I have

$$\left[\matrix{1 & 1 \cr 1 & 0 \cr}\right]^{n + 2} = \left[\matrix{1 & 1 \cr 1 & 0 \cr}\right] \left[\matrix{1 & 1 \cr 1 & 0 \cr}\right]^{n + 1} = \left[\matrix{1 & 1 \cr 1 & 0 \cr}\right] \left[\matrix{f_{n + 1} & f_n \cr f_n & f_{n - 1} \cr}\right] =$$

$$\left[\matrix{f_{n + 1} + f_n & f_n + f_{n - 1} \cr f_{n + 1} & f_n \cr}\right] = \left[\matrix{f_{n + 2} & f_{n + 1} \cr f_{n + 1} & f_n \cr}\right].$$

To get the last equality, I used the Fibonacci formulas

$$f_n + f_{n + 1} = f_{n + 2} \quad\hbox{and}\quad f_{n - 1} + f_n = f_{n + 1}.$$

Hence, the result is true for all $n \ge 1$ by induction.

32. A sequence of integers is defined by

$$x_0 = 5, \quad x_1 = 7,$$

$$x_n = x_{n - 1} + 20 x_{n-2} \quad\hbox{for}\quad n \ge 2.$$

Prove that

$$x_n = 3 \cdot 5^n + 2 \cdot (-4)^n \quad\hbox{for}\quad n \ge 0.$$

First,

$$3 \cdot 5^0 + 2 \cdot (-4)^0 = 3 + 2 = 5 = x_0.$$

$$3 \cdot 5^1 + 2 \cdot (-4)^1 = 3 \cdot 5 + 2 \cdot (-4) = 7 = x_1.$$

This establishes the result for $n = 0$ and $n = 1$ .

Assume the result is true for all $k < n$ :

$$x_k = 3 \cdot 5^k + 2 \cdot (-4)^k \quad\hbox{for}\quad k < n.$$

I will prove the result for n. I have

$$\eqalign{ x_n & = x_{n - 1} + 20 x_{n-2} \cr & = (3 \cdot 5^{n - 1} + 2 \cdot (-4)^{n - 1}) + 20(3 \cdot 5^{n-2} + 2 \cdot (-4)^{n-2}) \cr & = (3 \cdot 5^{n - 1} + 60 \cdot 5^{n-2}) + (2 \cdot (-4)^{n - 1} + 40 \cdot (-4)^{n-2}) \cr & = 3 \cdot 5^{n-2}(5 + 20) + 2 \cdot (-4)^{n-2}((-4) + 20) \cr & = 3 \cdot 5^{n-2} \cdot 5^2 + 2 \cdot (-4)^{n-2} \cdot (-4)^2 \cr & = 3 \cdot 5^n + 2 \cdot (-4)^n \cr}$$

This proves the result for n, so the result is true for all $n \ge 0$ by induction.

33. Use induction to prove that $n! > 3^n$ for $n \ge 7$ .

For $n = 7$ , $n! = 7! = 5040$ , while $3^7 = 2187$ . The result is true for $n = 7$ .

Let $n > 7$ , and suppose the result is true for n:

$$n! > 3^n.$$

Multiply both sides by $n + 1$ :

$$\eqalign{ (n + 1)! & = (n + 1) \cdot n! \cr & > (n + 1) \cdot 3^n \cr & > 3 \cdot 3^n \cr & = 3^{n + 1} \cr}$$

For the second inequality, I used the fact that $n > 7$ implies $n + 1 > 8 > 3$ .

This proves the result for $n + 1$ , so by induction the result is true for all $n \ge 7$ .

34. Let $n \in \integer^+$ . Prove that

$$9 \mid 10^n + 3 \cdot 4^{n + 2} + 5.$$

For $n = 1$ ,

$$10^n + 3 \cdot 4^{n + 2} + 5 = 10 + 192 + 5 = 207.$$

Since $9 \mid 207$ , the result holds for $n = 1$ .

Assume that the result holds for n:

$$9 \mid 10^n + 3 \cdot 4^{n + 2} + 5.$$

Write this divisibility statement as an equation:

$$10^n + 3 \cdot 4^{n + 2} + 5 = 9 k, \quad\hbox{for}\quad k \in \integer.$$

Then

$$10^n = 9 k - 3 \cdot 4^{n + 2} - 5.$$

The idea will be to substitute this into the $(n + 1)$ -expression, and simplify to get stuff divisible by 9.

I have

$$10^{n + 1} + 3 \cdot 4^{n+3} + 5 = 10 \cdot 10^n + 3 \cdot 4^{n+3} + 5 = 10(9 k - 3 \cdot 4^{n + 2} - 5) + 3 \cdot 4^{n+3} + 5 =$$

$$90 k - 30 \cdot 4^{n + 2} - 50 + 3 \cdot 4^{n+3} + 5 = (90 k - 45) + 3 \cdot 4^{n+3} - 30 \cdot 4^{n + 2} = (90 k - 45) + 3 \cdot 4^{n + 2}(4 - 10) =$$

$$(90 k - 45) + 3 \cdot 4^{n + 2}(-6) = (90 k - 45) - 18 \cdot 4^{n + 2} = 9(10 k - 5 - 2 \cdot 4^{n + 2}).$$

The last expression is divisible by 9. Hence, the result is true for $n + 1$ , and therefore true for all $n \ge 1$ by induction.

35. Let $f(x)$ be a polynomial with integer coefficients, and let $f'(x)$ be the derivative. Prove that

$$f(x + 3) = f(x) + 3 f'(x) \mod{9}.$$

I'll use induction on the degree of f.

Suppose $f(x) = k$ , where k is constant. Then

$$f(x + 3) = k, \quad\hbox{and}\quad f(x) + 3 f'(x) = k + 3\cdot 0 = k.$$

Therefore, the result is true for constant polynomials.

Let $n > 0$ . Assume the result is true for polynomials of degree n, and let $f(x)$ be a polynomial of degree $n + 1$ :

$$f(x) = a_0 + a_1 x + \cdots + a_n x^n + a_{n + 1} x^{n + 1}.$$

Then

$$f(x) = a_0 + x (a_1 + \cdots + a_n x^{n - 1} + a_{n + 1} x^n).$$

If I let $g(x) = a_1 + \cdots + a_n x^{n - 1} + a_{n + 1} x^n$ , then $g(x)$ is a polynomial of degree n. By the induction hypothesis,

$$g(x + 3) = g(x) + 3 g'(x) \mod{9}.$$

Now by the Product Rule,

$$f(x) = a_0 + x g(x), \quad\hbox{so}\quad f'(x) = x g'(x) + g(x).$$

Putting all this together,

$$f(x + 3) = a_0 + (x + 3) g(x + 3) = a_0 + (x + 3)(g(x) + 3 g'(x)) = (a_0 + x g(x)) + 3 (g(x) + x g'(x)) + 9 g'(x) =$$

$$f(x) + 3 f'(x) \mod{9}.$$

This completes the induction step, so the result is true for all polynomials, by induction.

36. Let x, y, and z be positive integers, and suppose the products $x y$ , $y z$ , and $x z$ are all perfect cubes. Prove that x, y, and z must be perfect cubes.

An integer is a perfect cube if and only if each prime in its prime factorization occurs to a power divisible by 3. (Can you prove this?)

Let p be a prime factor of x, and suppose $p^a$ is the biggest power of p which divides x. I want to show that a is divisible by 3.

Let $p^b$ be the biggest power of p which divides y, and let $p^c$ be the biggest power of p which divides z. Then $p^{a + b}$ is the biggest power of p dividing $x y$ , $p^{b + c}$ is the biggest power of p dividing $y z$ , and $p^{a + c}$ is the biggest power of p dividing $x z$ . Since $x y$ , $y z$ , and $x z$ are all perfect cubes,

$$3 \mid a + b, \quad 3 \mid b + c, \quad\hbox{and}\quad 3 \mid a + c.$$

Hence,

$$3 \mid (a + c) - (b + c) = a - b.$$

So

$$3 \mid (a + b) + (a - b) = 2 a.$$

But $(3, 2) = 1$ , so $3 \mid a$ .

Since p was an arbitrary prime dividing x, every prime dividing x occurs to a power which is a multiple of 3. Therefore, x is a perfect cube. By symmetry, the same is true of y and z.

37. Suppose that p, q, and r are distinct prime numbers,

$$x = p q^2 r^4, \quad y = p^a q^b, \quad\hbox{and}\quad y \mid x.$$

What are the possible values of y?

$y \mid x$ means $p^a q^b \mid p q^2 r^4$ , so $a \le 1$ and $b \le 2$ . Thus, $a = 0$ or 1 and $b = 0$ , 1, or 2. The possible values of y are

$$1, \quad p, \quad q, \quad p q, \quad q^2, \quad p q^2.\quad\halmos$$

38. Suppose that the prime factorization of an integer n is

$$n = p_1^3 \cdot p_2^6 \cdot p_3^5.$$

($p_1$ , $p_2$ , and $p_3$ are distinct primes.)

Write n as a product of integers $n = a b$ , where a is a perfect square and b is square-free --- that is, b is not divisible by the square of any positive integer except 1.

$$n = p_1^3 \cdot p_2^6 \cdot p_3^5 = (p_1 \cdot p_2^3 \cdot p_3^2)^2 (p_1 p_3).$$

$(p_1 \cdot p_2^3 \cdot p_3^2)^2$ is clearly a perfect square.

$p_1 p_3$ can't be divisible by a perfect square other than $1^2$ . To prove this, suppose that $d^2 \mid p_1 p_3$ , where d is a positive integer such that $d^2 \ne 1$ . Then $d \ne 1$ , so $d > 1$ , and d must be divisible by some prime number p by the Fundamental Theorem of Arithmetic. So $p \mid d$ , and hence

$$p^2 \mid d^2 \mid p_1 p_3.$$

Thus, p must be a prime factor of the number $p_1 p_3$ , and the power of p must be at least 2. But the prime factorization of $p_1 p_3$ is $p_1 p_3$ , and the distinct primes $p_1$ and $p_3$ both have power 1. This contradiction shows that $p_1 p_3$ is square-free.

39. Find the prime factorization of 15400 by trial division.

Divide 15400 by 2 as many times as possible:

$$\dfrac{15400}{2} = 7700, \quad \dfrac{7700}{2} = 3850, \quad \dfrac{3850}{2} = 1925.$$

Divide 1925 by 5 as many times as possible:

$$\dfrac{1925}{5} = 385, \quad \dfrac{385}{5} = 77.$$

Finally, it's clear that $77 = 7 \cdot 11$ . So

$$15400 = 2^3 \cdot 5^2 \cdot 7 \cdot 11.\quad\halmos$$

40. Use Fermat factorization to factor 25877 into primes. (You should use Fermat factorization rather than some other method, and you should show the trial values.)

First, $\sqrt{25877} \approx 160.863$ . So I will start my trials at 161.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & k & & $k^2 - 25877$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 161 & & 44 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 162 & & 367 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 163 & & 692 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 164 & & 1019 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 165 & & 1348 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 166 & & 1679 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 167 & & 2012 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 168 & & 2347 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 169 & & 2684 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 170 & & 3023 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 171 & & $3364 = 58^2$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

Therefore,

$$\eqalign{ 171^2 - 25877 & = 58^2 \cr 171^2 - 58^2 & = 25877 \cr (171 + 58)(171 - 58) & = 25877 \cr 229 \cdot 113 & = 25877 \cr}$$

You can check directly that 229 and 113 are prime, so this is the prime factorization.

41. Find the general solution to the Diophantine equation

$$6 x + 4 y = 10.$$

Since $(6, 4) = 2 \mid 10$ , there are solutions. By inspection, $x_0 = 1$ , $y_0 = 1$ is a particular solution. The general solution is

$$x = 1 + 2 t, \quad y = 1 - 3 t.\quad\halmos$$

42. Find the general solution to the Diophantine equation

$$7 x + 23 y = 18.$$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 7 & & - & & 3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 23 & & 0 & & 10 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 7 & & 3 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 3 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\eqalign{ 7 \cdot 10 + 23 \cdot (-3) & = 1\cr 7 \cdot 180 + 23 \cdot (-54) & = 18 \cr}$$

A particular solution is $x = 180$ and $y = -54$ . The general solution is

$$x = 180 + 23 t, \quad y = -54 - 7 t.\quad\halmos$$

43. Find the general solution to the Diophantine equation

$$6 x - 9 y + 15 z = 21.$$

Since $(6, 9, 15) = 3 \mid 21$ , there are solutions.

Note that $(6, 9) = 3$ . So write the equation in the form

$$3\left(\dfrac{6}{3}x - \dfrac{9}{3}y\right) + 15 z = 21.$$

Let

$$w = \dfrac{6}{3}x - \dfrac{9}{3}y = 2 x - 3 y.$$

Then

$$3 w + 15 z = 21.$$

$(3, 15) = 3 \mid 21$ , so there are solutions. By inspection, $w_0 = 2$ , $z_0 = 1$ is a particular solution. The general solution is

$$w = 2 + 5 s, \quad z = 1 - s.$$

Hence,

$$2 x - 3 y = w = 2 + 5 s.$$

$(2, -3) = 1 \mid 2 + 5 s$ , so there are solutions. To find a particular solution, write $(2, -3)$ as a linear combination of 2 and -3:

$$2 \cdot 2 + 1 \cdot (-3) = 1.$$

Multiply by $2 + 5 s$ :

$$2(2 + 5 s) \cdot 2 + (2 + 5 s) \cdot (-3) = 2 + 5 s.$$

Hence, $x_0 = 2(2 + 5 s)$ , $y_0 = 2 + 5 s$ is a particular solution. The general solution is

$$x = 2(2 + 5 s) - 3 t = 4 + 10 s - 3 t, \quad y = 2 + 5 s - 2 t.$$

(Note: You might have expected the "$-3 t$ " and "$-2 t$ " terms to have opposite signs. The reason they don't is that the coefficients of the x and y terms in the original equation are "+" and "-", instead of both "+" as is often the case.)

All together, the solution to the original equation is

$$x = 4 + 10 s - 3 t, \quad y = 2 + 5 s - 2 t, \quad z = 1 - s.\quad\halmos$$

44. Bonzo buys some books that cost $7 each and some books that cost $15 each. The books cost a total of $349. What is the largest total number of books Bonzo could have bought?

Let x be the number of $7 books and y be the number of $15 books. Then

$$7 x + 15 y = 349.$$

$$\eqalign{ 7 \cdot (-2) + 15 \cdot 1 & = 1 \cr 7 \cdot (-698) + 15 \cdot 349 & = 349 \cr}$$

$x = -698$ and $y = 349$ is a particular solution. The general solution is

$$x = -698 + 15 t, \quad y = 349 - 7 t.$$

Since the numbers of books can't be negative, I have $x \ge 0$ and $y \ge 0$ .

$$x \ge 0 \quad\hbox{gives}\quad -698 + 15 t \ge 0, \quad\hbox{so}\quad t \ge \dfrac{698}{15} \approx 46.53333 \ldots.$$

$$y \ge 0 \quad\hbox{gives}\quad 349 - 7 t \ge 0, \quad\hbox{so}\quad t \le \dfrac{349}{7} \approx 49.85714 \ldots.$$

The integer values of t satisfying both inequalities are $t = 47, 48, 49$ .

The total number of books is

$$x + y = (-698 + 15 t) + (349 - 7 t) = -349 + 8 t.$$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & t & & x & & y & & $x + y$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 47 & & 7 & & 20 & & 27 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 48 & & 22 & & 13 & & 35 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 49 & & 37 & & 6 & & 43 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The largest total number of books is 43, consisting of 37 7-dollar books 6 15-dollar books.

45. I. M. Snarky buys 43 apples and oranges. The apples cost 10 cents more than the oranges, and he spends a total of $30.68. Find the number of each fruit that he bought and their prices.

I will do everything in cents.

Let x be the number of apples, and let y be the number of oranges. Then

$$x + y = 43, \quad\hbox{so}\quad y = 43 - x.$$

Suppose the oranges cost c cents each. Then the apples cost $c + 10$ cents each. The total cost of the fruit is

$$3068 = x(c + 10) + (43 - x)c = 10 x + 43 c.$$

By trial and error or the Extended Euclidean Algorithm, I have

$$\eqalign{ 1 & = 10 \cdot 13 + 43 \cdot (-3) \cr 3068 & = 10 \cdot 39884 + 43 \cdot (-9204) \cr}$$

Thus, a particular solution is $x = 39884$ and $c = -9204$ , and the general solution is

$$\eqalign{ x & = 39884 - 43 t \cr c & = -9204 + 10 t \cr}$$

Now $x > 0$ , so

$$\eqalign{ 39884 - 43 t & > 0 \cr 39884 & > 43 t \cr \noalign{\vskip2 pt} \dfrac{39884}{43} & > t \cr}$$

Since $\dfrac{39884}{43} \approx 927.53488$ , I have $t \le 927$ .

Also, $c > 0$ , so

$$\eqalign{ -9204 + 10 t & > 0 \cr 10 t & > 9204 \cr \noalign{\vskip2 pt} t & > \dfrac{9204}{10} \cr}$$

Thus, $t > 920.4$ , so $t \ge 921$ .

All together, I find that t is an integer and $921 \le t \le 927$ . I check the values:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & t & & $x = 39884 - 43 t$ & & $y = 43 - s$ & & $c = -9204 + 10 t$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 921 & & 281 & & -238 & & 6 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 922 & & 238 & & -195 & & 16 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 923 & & 195 & & -152 & & 26 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 924 & & 152 & & -109 & & 36 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 925 & & 109 & & -66 & & 46 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 926 & & 66 & & -23 & & 56 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 927 & & 23 & & 20 & & 66 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

He bought 23 apples and 20 oranges. The apples cost 76 cents each, and the oranges cost 66 cents each.

46. Solve the following Diophantine equation by factoring:

$$x^2 = 7 + 4 y^2.$$

Rewrite the equation:

$$\eqalign{ x^2 & = 7 + 4 y^2 \cr x^2 - 4 y^2 & = 7 \cr (x + 2 y)(x - 2 y) & = 7 \cr}$$

7 may be factored into the product of two integers in 4 ways. I'll take cases.

Case 1: $x + 2 y = 1$ and $x - 2 y = 7$ .

Subtracting the equations gives $4 y = -6$ , which has no integer solutions.

Case 2: $x + 2 y = 7$ and $x - 2 y = 1$ .

Subtracting the equations gives $4 y = 6$ , which has no integer solutions.

Case 3: $x + 2 y = -1$ and $x - 2 y = -7$ .

Subtracting the equations gives $4 y = 6$ , which has no integer solutions.

Case 4: $x + 2 y = -7$ and $x - 2 y = -1$ .

Subtracting the equations gives $4 y = -6$ , which has no integer solutions.

Therefore, the original Diophantine equation has no solutions.

47. Is $4 \cdot 3^{1000} + 7^{1000}$ prime?

Note that

$$3^4 = 81 = 1 \mod{10} \quad\hbox{and}\quad 7^4 = 2401 = 1 \mod{10}.$$

So

$$4 \cdot 3^{1000} + 7^{1000} = 4 \cdot (3^4)^{2500} + (7^4)^{2500} = 4 \cdot 1^{2500} + 1^{2500} = 4 + 1 = 5 \mod{10}.$$

This means that the units digit of $4 \cdot 3^{1000} + 7^{1000}$ is 5. Since $4 \cdot 3^{1000} + 7^{1000}$ is obivously greater than 5, it's not prime because it's divisible by 5.

48. Find $52^{-1} \mod{77}$ .

Use the Extended Euclidean algorithm:

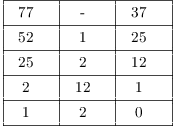
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 77 & & - & & 37 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 52 & & 1 & & 25 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 25 & & 2 & & 12 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 12 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\eqalign{ 25 \cdot 77 + (-37) \cdot 52 & = 1 \cr (-37) \cdot 52 & = 1 \mod{77} \cr 40 \cdot 52 & = 1 \mod{77} \cr}$$

Hence, $52^{-1} = 40 \mod{77}$ .

49. Suppose that $(m, n) = 1$ . Prove that if $a = b \mod{m}$ and $a = b \mod{n}$ , then $a = b \mod{m n}$ .

Since $(m, n) = 1$ , I have

$$c m + d n = 1 \quad\hbox{for}\quad c, d \in \integer.$$

Likewise, since $a = b \mod{m}$ and $a = b \mod{n}$ , I have

$$a - b = j m \quad\hbox{and}\quad a - b = k n \quad\hbox{for}\quad j, k \in \integer.$$

Then

$$\eqalign{ c m + d n & = 1 \cr c m (a - b) + d n (a - b) & = a - b \cr c m k n + d n j m & = a - b \cr m n (c k + d j) & = a - b \cr}$$

Thus, $m n \mid a - b$ , so $a = b \mod{m n}$ .

50. Prove that if $n \in \integer$ , then $n^3 + 4 n + 2$ is not divisible by 5.

If $n \in \integer$ , then $n = 0, 1, 2, 3, 4 \mod{5}$ . Contruct a table:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $n \mod{5}$ & & 0 & & 1 & & 2 & & 3 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $n^3 + 4 n + 2 \mod{5}$ & & 2 & & 2 & & 3 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

In every case, $n^3 + 4 n + 2 \ne 0 \mod{5}$ . Hence, if $n \in \integer$ , then $n^3 + 4 n + 2$ is not divisible by 5.

51. (a) Construct a table for multiplication mod 8.

(b) What is the multiplicative inverse of 5 mod 8?

(b)

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot$ & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & & 7 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 0 & & 0 & & 0 & & 0 & & 0 & & 0 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & & 7 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 0 & & 2 & & 4 & & 6 & & 0 & & 2 & & 4 & & 6 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 0 & & 3 & & 6 & & 1 & & 4 & & 7 & & 2 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 4 & & 0 & & 4 & & 0 & & 4 & & 0 & & 4 & & 0 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 5 & & 0 & & 5 & & 2 & & 7 & & 4 & & 1 & & 6 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 6 & & 0 & & 6 & & 4 & & 2 & & 0 & & 6 & & 4 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 7 & & 0 & & 7 & & 6 & & 5 & & 4 & & 3 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

(b) Since $5 \cdot 5 = 1 \mod{8}$ , the multiplicative inverse of 5 mod 8 is 5.

52. Prove by contradiction that 15 does not have a multiplicative inverse mod 42.

Suppose $15 x = 1 \mod{42}$ . I notice that $(15, 42) = 3$ , and $3 \cdot 14 = 42$ . Multiply the equation by 14 and simplify:

$$\eqalign{ 14 \cdot 15 x = 14 \cdot 1 \mod{42} \cr 210 x & = 14 \mod{42} \cr 0 & = 14 \mod{42} \cr}$$

This contradiction proves that 15 does not have a multiplicative inverse mod 42.

53. Prove that if n is a positive integer, then

$$7^n = 6 n + 1 \mod{36}.$$

Method 1. Write $7^n = (6 + 1)^n$ and expand the right side using the Binomial Formula:

$$7^n = 6^n + {n \choose 1} 6^{n-1} + \cdots + {n \choose {n - 2}} 6^2 + {n \choose {n - 1}} 6 + 1.$$

All of the terms except the last two are divisible by $6^2 = 36$ . Therefore,

$$7^n = {n \choose {n - 1}} 6 + 1 = 6 n + 1 \mod{36}.$$

Method 2. I'll use induction. For $n = 1$ ,

$$7^1 = 7 \quad\hbox{and}\quad 6 \cdot 1 + 1 = 7.$$

So the two sides are equal (so they're equal mod 36).

Assume the result is true for n:

$$7^n = 6 n + 1 \mod{36}.$$

I'll prove it for $n + 1$ :

$$\eqalign{ 7^{n + 1} & = 7 \cdot 7^n \mod{36} \cr & = 7 (6 n + 1) \mod{36} \cr & = 42 n + 7 \mod{36} \cr & = 6 n + 7 \mod{36} \cr & = 6(n + 1) + 1 \mod{36} \cr}$$

This proves the result for $n + 1$ , so it's true for all $n \ge 1$ , by induction.

54. By constructing a table, show that $x^2 + 3 x + 2 = 0 \mod{6}$ has 4 solutions mod 6. (Note that quadratics "usually" have at most two roots!)

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 + 3 x + 2 \mod{6}$ & & 2 & & 0 & & 0 & & 2 & & 0 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The solutions mod 6 are $x = 1$ , $x = 2$ , $x = 4$ , and $x = 5$ .

55. (a) Prove that the sum of the cubes of two integers does not leave a remainder of 4 when the sum is divided by 7.

(b) Prove that the Diophantine equation $x^3 + y^3 = 4$ has no solutions.

(a) Make a table of cubes mod 7:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $n \mod{7}$ & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $n^3 \mod{7}$ & & 0 & & 1 & & 1 & & 6 & & 1 & & 6 & & 6 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The possible values of $n^3 \mod{7}$ are 0, 1, and 6. There is no way to make 4 as the sum of two of these numbers. Hence, if $m, n \in \integer$ , then $m^3 + n^3 \ne 4 \mod{7}$ . This means that the sum of the cubes of two integers does not leave a remainder of 4 when the sum is divided by 7.

(b) If $x^3 + y^3 = 4$ for $x, y \in \integer$ , then $x^3 + y^3 = 4 \mod{7}$ . But part (a) shows that $x^3 + y^3 = 4 \mod{7}$ has no solutions. Hence, the Diophantine equation $x^3 + y^3 = 4$ has no solutions.

Note: This method can sometimes be used to show that a Diophantine equation has no solutions. One problem here is to choose a good modulus. For instance, it would not help to reduce $x^3 + y^3 = 4$ mod 2, since $x^3 + y^3 = 4 = 0 \mod{2}$ does have solutions.

When a dog runs at you, whistle for him. - Henry David Thoreau

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga