Review Sheet for Test 2

Math 393

These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the absence of a topic does not imply that it won't appear on the test.

1. Solve the congruence

$$6 x + 7 = 4 \mod{13}.$$

2. Solve the congruence

$$6 x + 15 y = 12 \mod{9}.$$

3. Find all solutions to the congruence

$$x^{120} + 31 x = 3 \mod{61}.$$

4. Solve the system of congruences:

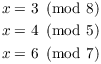
$$\eqalign{ x & = 3 \mod{8} \cr x & = 4 \mod{5} \cr x & = 6 \mod{7} \cr}$$

5. Find the smallest integer which leaves a remainder of 11 when divided by 13, leaves a remainder of 5 when divided by 8, and leaves a remainder of 7 when divided by 9.

6. Solve the system of congruences

$$\eqalign{ x & = 3 \mod{12} \cr x & = 15 \mod{18} \cr}$$

(Note that the moduli aren't relatively prime, so you can't use the method of the Chinese Remainder Theorem proof. Solve directly using algebra instead.)

7. (a) Solve the congruence

$$12 x = 14 \mod{9}.$$

(b) Solve the congruence

$$12 x = 28 \mod{10}.$$

(c) Solve the congruence

$$3 x + 7 y = 9 \mod{11}.$$

8. Consider the system of congruences

$$\matrix{ 4 x & + & 2 y & = & 3 \mod{7} \cr x & + & 3 y & = & 1 \mod{7} \cr}.$$

Solve the system by:

(a) Using ordinary algebra.

(b) Inverting the coefficient matrix.

(c) Using Cramer's Rule.

9. Find the least positive residue of $171^{219}$ mod 13.

10. How many zeros does the decimal expansion of $400!$ end in?

11. Reduce $10^{16425} \mod{47}$ to a number in the range $\{0, 1, \ldots, 46\}$ .

12. Reduce $68^{174} \mod{89}$ to a number in the range $\{0, 1, \ldots 88\}$ .

13. What is the remainder when $104!$ is divided by 107?

14. Reduce $106! \mod{11663}$ to a number in the range $\{0, 1, \ldots, 11662\}$ . (Note: $11663 = 107 \cdot 109$ , and 107 and 109 are prime.)

15. Simplify $\dfrac{96!}{52} \mod{97}$ to a number in the range $\{0, 1, \ldots, 96\}$ .

16. For what prime numbers p does p divide $2^p + 1$ ?

17. Solve $x^{38} - 3 x^{19} + 2 = 0 \mod{19}$ .

18. (a) By making a table, find all solutions to

$$x^4 + 19 x + 12 = 0 \mod{11}.$$

(b) For each solution you found in (a), generate a solution to

$$x^4 + 19 x + 12 = 0 \mod{121}.$$

(Alternatively, show that this is not possible.)

19. Compute $\phi(2^3 \cdot 3^2 \cdot 5)$ .

20. Suppose $\phi(n) = n - 1$ . How many positive factors does n have?

21. Suppose that $(n, 108) = 1$ . Prove that $n^{36} = 1 \mod{108}$ .

22. Reduce $107^{1002} \mod{100}$ to a number in the range $\{0, 1, \ldots, 99\}$ .

23. Prove that if $(n, 72) = 1$ , then $n^{12} = 1 \mod{72}$ .

24. Find the last three digits (units, tens, and hundreds) of $17^{40003}$ .

25. Compute $\phi(96)$ , $\mu(105)$ , $\sigma(108)$ , and $\tau(1000)$ .

26. What positive integers have exactly three positive divisors?

27. Suppose that $\phi(m) = 32 n$ , where n is an odd number. Prove that m has no more than 5 different odd prime divisors.

28. Suppose that $\phi(n) = 28$ .

(a) Show that if p is a prime and $p \ge 31$ , then $p \notdiv n$ .

(b) Show that the largest power of 3 that can divide n is $3^1$ .

(c) Show that $7 \notdiv n$ .

29. Let n be the square of an odd integer. Prove that $\sigma(n)$ is odd.

30. Find all positive integers n such that $\sigma(n) = n + 7$ .

31. For what integers $n \ge 1$ is $\tau(n)$ an odd number?

32. Let p be prime. Show that $\dfrac{\phi(p) \cdot \sigma(p) + 1}{p} = p$ .

33. Give a set of infinitely many integers n such that $18 \mid \phi(n)$ .

34. Prove that if $\phi(n) \mid n - 1$ , then n is square-free --- that is, there is no prime p such that $p^2 \mid n$ .

35. Find all positive integers n satisfying $7 \mid n$ and $\phi(n) = 18$ .

36. In each case, if the function is multiplicative, prove it; if it is not, give a specific counterexample.

(a) $f: \integer^+ \to \real$ given by

$$f(x) = x + 1.$$

(b) $g: \integer^+ \to \real$ given by

$$g(x) = \sqrt{x}.$$

37. Let $D f$ denote the divisor sum of the arithmetic function f. Suppose $f(x) = x^2$ . Compute $(D f)(10)$ .

38. Find $(2^{36} - 1, 2^{42} - 1)$ .

39. Find a proper factor of $2^{29} - 1$ .

Solutions to the Review Sheet for Test 2

1. Solve the congruence

$$6 x + 7 = 4 \mod{13}.$$

Add 6 to both sides (using the fact that $7 + 6 = 0 \mod{13}$ :

$$6 x = 10 \mod{13}.$$

I want a reciprocal of 6 mod 13. Note that $(6, 13) = 1$ . Express $(6, 13)$ as a linear combination of 6 and 13:

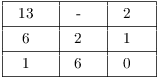
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 13 & & - & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 6 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 6 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus,

$$1 \cdot 13 + (-2) \cdot 6 = 1, \quad\hbox{so}\quad (-2) \cdot 6 = 1 \mod{13}.$$

Now $-2 = 11 \mod{13}$ , so 11 is the reciprocal of 6 mod 13. Multiply both sides of the equation by 11, and reduce the right side:

$$x = 110 = 6 \mod{13}.\quad\halmos$$

2. Solve the congruence

$$6 x + 15 y = 12 \mod{9}.$$

Determine the parameter ranges which give the correct number of solutions mod 9.

Since $(6, 15, 9) = 3 \mid 12$ , there are $3 \cdot 9 = 27$ solutions mod 9.

Rewrite the equation as a Diophantine equation:

$$6 x + 15 y + 9 z = 12, \quad 2 x + 5 y + 3 z = 4.$$

Set $w = 2 x + 5 y$ , so

$$w + 3 z = 4.$$

$w_0 = 1$ , $z_0 = 1$ is a particular solution. The general solution is

$$w = 3 s + 1, \quad z = -s + 1.$$

Now

$$3 s + 1 = w = 2 x + 5 y.$$

$x_0 = -s - 2$ , $y_0 = s + 1$ is a particular solution. (I juggled the numbers: $2 \cdot (-s) + 5 \cdot s = 3 s$ and $2 \cdot (-2) + 5 \cdot 1 = 1$ . The point is that you can do the s-part and the number part independently.) The general solution is

$$x = 5 t - s - 2, \quad y = -2 t + s + 1.$$

Taking everything mod 9,

$$x = 5 t + 8 s + 7 \mod{9}, \quad y = 7 t + s + 1 \mod{9}.\quad\halmos$$

Note: It turns out that $s = 0, 1, 2$ and $t = 0, 1, \ldots, 8$ will give 27 independent solutions.

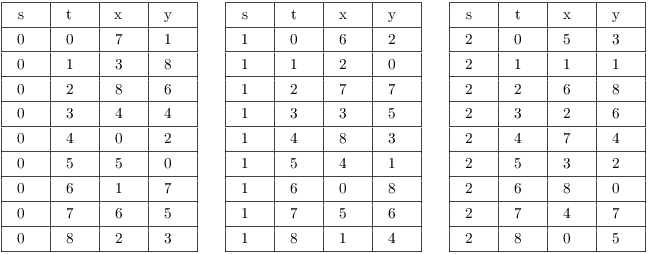
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & s & & t & & x & & y & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 7 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 1 & & 3 & & 8 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 2 & & 8 & & 6 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 3 & & 4 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 4 & & 0 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 5 & & 5 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 6 & & 1 & & 7 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 7 & & 6 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 8 & & 2 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} \hskip0.25 in \vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & s & & t & & x & & y & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & 6 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 2 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 7 & & 7 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 3 & & 3 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 4 & & 8 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 5 & & 4 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 6 & & 0 & & 8 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 7 & & 5 & & 6 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 8 & & 1 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} \hskip0.25 in \vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & s & & t & & x & & y & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 0 & & 5 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 1 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 6 & & 8 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 3 & & 2 & & 6 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 4 & & 7 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 5 & & 3 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 6 & & 8 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 7 & & 4 & & 7 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 8 & & 0 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

There are indeed 27 distinct solutions mod 9, so those are all the solutions.

3. Find all solutions to the congruence

$$x^{120} + 31 x = 3 \mod{61}.$$

If $61 \mid x$ , then $x = 0 \mod{61}$ , so $x^{120} + 31 x = 0 \ne 3 \mod{61}$ . This does not give a solution.

Suppose that $61 \notdiv x$ . By Fermat's Theorem, $x^{60} = 1 \mod{61}$ , so $x^{120} = (x^{60})^2 = 1 \mod{61}$ . The equation becomes

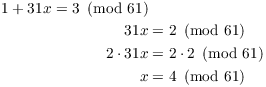
$$\eqalign{ 1 + 31 x = 3 \mod{61} \cr 31 x & = 2 \mod{61} \cr 2 \cdot 31 x & = 2 \cdot 2 \mod{61} \cr x & = 4 \mod{61} \cr}$$

The solution is $x = 4 \mod{61}$ .

4. Solve the system of congruences:

$$\eqalign{ x & = 3 \mod{8} \cr x & = 4 \mod{5} \cr x & = 6 \mod{7} \cr}$$

The moduli 8, 5, and 7 are pairwise relatively prime, so there is a unique solution mod $8 \cdot 5 \cdot 7 = 280$ , by the Chinese Remainder Theorem.

You can solve the system using the formulas given in the proof of the Chinese Remainder Theorem, or you can solve the congruences iteratively, using basic algebra and modular arithmetic. I'll take the second approach, but the first approach is fine (provided that you can recall the formulas exactly).

First, $x = 3 \mod{8}$ means that

$$x = 3 + 8 s.$$

Substitute this in the second equation:

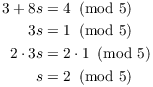
$$\eqalign{ 3 + 8 s & = 4 \mod{5} \cr 3 s & = 1 \mod{5} \cr 2 \cdot 3 s & = 2 \cdot 1 \mod{5} \cr s & = 2 \mod{5} \cr}$$

$s = 2 \mod{5}$ means that $s = 2 + 5 t$ , so

$$x = 3 + 8(2 + 5 t) = 19 + 40 t.$$

Substitute this in the third equation:

$$\eqalign{ 19 + 40 t & = 6 \mod{7} \cr 5 t & = -13 = 1 \mod{7} \cr 3 \cdot 5 t & = 3 \cdot 1 \mod{7} \cr t & = 3 \mod{7} \cr}$$

$t = 3 \mod{7}$ means that $t = 3 + 7 u$ , so

$$x = 19 + 40(3 + 7 u) = 139 + 280 u, \quad\hbox{or}\quad x = 139 \mod{280}.\quad\halmos$$

5. Find the smallest integer which leaves a remainder of 11 when divided by 13, leaves a remainder of 5 when divided by 8, and leaves a remainder of 7 when divided by 9.

The conditions in the problem are equivalent to the system of congruences

$$\eqalign{ x & = 11 \mod{13} \cr x & = 5 \mod{8} \cr x & = 7 \mod{9} \cr}$$

$x = 11 \mod{13}$ gives $x = 11 + 13 a$ . Plugging this into the second congruence gives

$$\eqalign{ 11 + 13 a & = 5 \mod{8} \cr 13 a & = -6 = 2 \mod{8} \cr 5 a & = 2 \mod{8} \cr 5 \cdot 5 a & = 5 \cdot 2 \mod{8} \cr a & = 10 = 2 \mod{8} \cr}$$

The last congruence gives $a = 2 + 8 b$ . Plugging this into $x = 11 + 13 a$ , I get

$$x = 11 + 13(2 + 8 b) = 37 + 104 b.$$

Substituting this into the third congruence yields

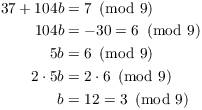
$$\eqalign{ 37 + 104 b & = 7 \mod{9} \cr 104 b & = -30 = 6 \mod{9} \cr 5 b & = 6 \mod{9} \cr 2 \cdot 5 b & = 2 \cdot 6 \mod{9} \cr b & = 12 = 3 \mod{9} \cr}$$

The last congruence gives $b = 3 + 9 c$ . Plugging this into $x = 37 + 104 b$ , I get

$$x = 37 + 104(3 + 9 c) = 349 + 936 c, \quad\hbox{or}\quad x = 349 \mod{936}.\quad\halmos$$

6. Solve the system of congruences

$$\eqalign{ x & = 3 \mod{12} \cr x & = 15 \mod{18} \cr}$$

Since $(12, 18) = 6 \mid 15 - 3$ , the system has solutions. Since the moduli are not relatively prime, I can't use the formulas in the Chinese Remainder Theorem. Instead, I'll use the algebraic approach.

$x = 3 \mod{12}$ gives $x = 3 + 12 a$ . Plugging this into the second congruence, I get

$$\eqalign{ 3 + 12 a & = 15 \mod{18} \cr 12 a & = 12 \mod{18} \cr}$$

I want to divide the 12's by 12. To do this, I must divide the modulus 18 by $(12, 18) = 6$ . I get

$$a = 1 \mod{3}, \quad\hbox{so}\quad a = 1 + 3 b.$$

Plugging this into $x = 3 + 12 a$ , I get

$$x = 3 + 12(1 + 3 b) = 15 + 36 b, \quad\hbox{or}\quad x = 15 \mod{36}.\quad\halmos$$

7. (a) Solve the congruence

$$12 x = 14 \mod{9}.$$

(b) Solve the congruence

$$12 x = 28 \mod{10}.$$

(c) Solve the congruence

$$3 x + 7 y = 9 \mod{11}.$$

(a) Since $(12, 9) = 3 \notdiv 14$ , the congruence has no solutions.

(b) Since $(12, 10) = 2 \mid 28$ , there are solutions. The congruence can be written as

$$4(3 x) = 4(7) \mod{10}.$$

If I cancel the common factor of 4, I must divide the modulus by $(4, 10) = 2$ . This gives

$$3 x = 7 \mod {5}, \quad\hbox{or}\quad 3 x = 2 \mod{5}.$$

Since $3^{-1} = 2 \mod{5}$ , multiplying by 2 yields

$$x = 4 \mod{5}.$$

The original congruence was mod 10. The numbers in the set 0, 1, ... 9 which satisfy $x = 4 \mod{5}$ are 4 and 9. Therefore, the solution is $x = 4 \mod{10}$ or $x = 9 \mod{10}$ .

(c) One approach is to convert the congruence to a Diophantine equation. But since the modulus is prime, it's easier to regard the congruence as a system of congruences mod 11 which happens to have only one equation! I'll row reduce the augmented matrix to row-reduced echelon form:

$$\left[\matrix{3 & 7 & 9 \cr}\right] \matrix{\to \cr r_1\to 4 r_1 \cr} \left[\matrix{1 & 6 & 3 \cr}\right]$$

(I multiplied by 4 because $4 = 3^{-1} \mod{11}$ .) The last matrix says

$$x + 6 y = 3 \mod{11}, \quad\hbox{or}\quad x = 5 y + 3 \mod{11}.$$

Set $y = s \mod{11}$ . Then $x = 5 s + 3 \mod{11}$ . The solution is

$$x = 5 s + 3 \mod{11}, \quad y = s \mod{11}.\quad\halmos$$

8. Consider the system of congruences

$$\matrix{ 4 x & + & 2 y & = & 3 \mod{7} \cr x & + & 3 y & = & 1 \mod{7} \cr}.$$

Solve the system by:

(a) Using ordinary algebra.

(b) Inverting the coefficient matrix.

(c) Using Cramer's Rule.

(a) Multiply the second equation by 4 and subtract it from the first equation to eliminate x:

$$\eqalign{ 4 x + 2 y & = 3 \mod{7} \cr 4 x + 5 y & = 4 \mod{7} \cr \noalign{\vskip2 pt \hrule \vskip2 pt} -3 y & = -1 \mod{7} \cr (-5)(-3 y) & = (-5)(-1) \mod{7} \cr y & = 5 \mod{7} \cr}$$

Substitute this into $x + 3 y = 1 \mod{7}$ and solve for x:

$$\eqalign{ x + 15 & = 1 \mod{7} \cr x + 1 & = 1 \mod{7} \cr x & = 0 \mod{7} \quad\halmos \cr}$$

(b) The matrix form is

$$\left[\matrix{4 & 2 \cr 1 & 3 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{3 \cr 1 \cr}\right].$$

To solve the system by inverting the coeffient matrix, multiply both sides by the inverse of the coefficient matrix:

$$\left[\matrix{4 & 2 \cr 1 & 3 \cr}\right]^{-1} \left[\matrix{4 & 2 \cr 1 & 3 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{4 & 2 \cr 1 & 3 \cr}\right]^{-1} \left[\matrix{3 \cr 1 \cr}\right] = 3^{-1} \cdot \left[\matrix{3 & 5 \cr 6 & 4 \cr}\right] \left[\matrix{3 \cr 1 \cr}\right] =$$

$$5 \cdot \left[\matrix{3 & 5 \cr 6 & 4 \cr}\right] \left[\matrix{3 \cr 1 \cr}\right] = \left[\matrix{0 \cr 5 \cr}\right].$$

The solution is $x = 0 \mod{7}$ and $y = 5 \mod{7}$ .

(c) The matrix form is

$$\left[\matrix{4 & 2 \cr 1 & 3 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{3 \cr 1 \cr}\right].$$

I have

$$\det \left[\matrix{4 & 2 \cr 1 & 3 \cr}\right] = (4)(3) - (1)(2) = 10 = 3 \mod{7},$$

$$\det \left[\matrix{3 & 2 \cr 1 & 3 \cr}\right] = (3)(3) - (1)(2) = 7 = 0 \mod{7},$$

$$\det \left[\matrix{4 & 3 \cr 1 & 1 \cr}\right] = (4)(1) - (3)(1) = 1 \mod{7}.$$

Notice that in the second and third determinants, I replaced the first and second columns, respectively, of the coefficient matrix by the constant matrix $\left[\matrix{3 \cr 1 \cr}\right]$ .

Note that $3^{-1} = 5 \mod{7}$ . So by Cramer's Rule,

$$x = 5 \cdot 0 = 0 \mod{7} \quad\hbox{and}\quad y = 5 \cdot 1 = 5 \mod{7}.\quad\halmos$$

9. Find the least positive residue of $171^{219}$ mod 13.

First, $171 = 2 \mod{13}$ , so $171^{219} = 2^{219} \mod{13}$ .

Since $13 \notdiv 2$ , Fermat's Theorem gives $2^{12} = 1 \mod{13}$ . Since $219 = 12 \cdot 18 + 3$ , I have

$$2^{219} = (2^{12})^{18} \cdot 2^3 = 1 \cdot 8 = 8 \mod{13}.$$

That is, $171^{219} = 8 \mod{13}$ .

10. How many zeros does the decimal expansion of $400!$ end in?

The number of zeros that the decimal expansion of $400!$ ends in is equal to the number of factors of 10 which divide $400!$ .

Since $10 = 2 \cdot 5$ and since 5 is greater than 2, the number of factors of 10 which divide $400!$ is equal to the number of factors of 5 which divide $400!$ . Now $400!$ is the product of the numbers in $\{1, 2, 3, \ldots, 400\}$ . Factors of 5 come from three kinds of numbers in this set:

(a) Numbers divisible by 5 but not 25 contribute 1 factor of 5.

(b) Numbers divisible by 25 by not 125 contribute 2 factors of 5.

(c) Numbers divisible by 125 contribute 3 factors of 5.

(There are no numbers in the set divisible by the next power of 5, which is 625.)

The number of numbers in the set divisible by 5 is $\left[\dfrac{400}{5}\right] = 80$ .

The numbers divisible by 25 contribute 2 factors of 5, but one of the contributions was counted when I counted the numbers divisible by 5. So I just count them once: There are $\left[\dfrac{400}{25}\right] = 16$ .

Likewise, the numbers divisible by 125 contribute 3 factors of 5, but one of the contributions was counted when I counted the numbers divisible by 5, and another when I counted the numbers divisible by 25. So I just count them once: There are $\left[\dfrac{400}{125}\right] = 3$ .

Hence, the total number of factors of 5, and the number of zeros in the decimal expansion, is $80 + 16 + 3 = 99$ .

11. Reduce $10^{16425} \mod{47}$ to a number in the range $\{0, 1, \ldots, 46\}$ .

Since 47 is prime and $47 \notdiv 10$ , $10^{46} = 1 \mod{47}$ by Fermat's theorem. Now

$$16425 = 46 \cdot 357 + 3.$$

Hence,

$$10^{16425} = (10^{46})^{357}\cdot 10^3 = 1000 = 13 \mod{47}.\quad\halmos$$

12. Reduce $68^{174} \mod{89}$ to a number in the range $\{0, 1, \ldots 88\}$ .

89 is prime, and $89 \notdiv 68$ . By Fermat's theorem,

$$68^{88} = 1 \mod{89}.$$

Hence,

$$\eqalign{ x & = 68^{174} \mod{89} \cr x & = 68^{88} \cdot 68^{86} \mod{89} \cr x & = 68^{86} \mod{89} \cr 68^2 \cdot x & = 68^{88} \mod{89} \cr 4624 x & = 1 \mod{89} \cr 85 x & = 1 \mod{89} \cr}$$

By the Extended Euclidean algorithm, $85^{-1} = 22 \mod{89}$ . So

$$\eqalign{ 22 \cdot 85 x & = 22 \cdot 1 \mod{89} \cr x & = 22 \mod{89} \quad\halmos \cr}$$

13. What is the remainder when $104!$ is divided by 107?

Note that 107 is prime. By Wilson's theorem,

$$-1 = 106! = 106 \cdot 105 \cdot 104! = (-1) \cdot (-2) \cdot 104! = 2 \cdot 104! \mod{107}.$$

Since $54 \cdot 2 = 108 = 1 \mod{107}$ ,

$$54 \cdot (-1) = (54 \cdot 2) \cdot 104! = 104! \mod{107}.$$

Therefore,

$$104! = -54 = 53 \mod{107}.$$

$104!$ leaves a remainder of 53 when it's divided by 107.

14. Reduce $106! \mod{11663}$ to a number in the range $\{0, 1, \ldots, 11662\}$ .

Let $x = 106!$ . Then

$$x = 106! = -1 \mod{107}.$$

Next,

$$\eqalign{ x & = 106! \mod{109} \cr 107 \cdot 108 \cdot x & = 107 \cdot 108 \cdot 106! \mod{109} \cr (-2)(-1) x & = 108! \mod{109} \cr 2 x & = -1 \mod{109} \cr 55 \cdot 2 x & = 55 \cdot (-1) \mod{109} \cr x & = -55 = 54 \mod{109} \cr}$$

Now $x = -1 \mod{107}$ gives $x = -1 + 107 a$ . So

$$\eqalign{ -1 + 107 a & = 54 \mod{109} \cr 107 a & = 55 \mod{109} \cr -2 a & = 55 \mod{109} \cr (-55) \cdot (-2 a) & = (-55) \cdot 55 \mod{109} \cr a & = -3025 = 27 \mod{109} \cr a & = 27 + 109 b \cr}$$

So

$$\eqalign{ x & = -1 + 107(27 + 109 b) = 2888 + 11663 b \cr x & = 2888 \mod{11663} \quad\halmos \cr}$$

15. Simplify $\dfrac{96!}{52} \mod{97}$ to a number in the range $\{0, 1, \ldots, 96\}$ .

By Wilson's theorem, $96! = -1 \mod{97}$ . So

$$\eqalign{ x & = \dfrac{96!}{52} \mod{97} \cr \noalign{\vskip2 pt} 52 x & = 96! = -1 \mod{97} \cr}$$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 97 & & - & & 28 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 52 & & 1 & & 15 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 45 & & 1 & & 13 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 7 & & 6 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 3 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 3 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$1 = (52, 97) = 28 \cdot 52 + (-15) \cdot 97.$$

It follows that $52^{-1} = 28 \mod{97}$ , so

$$\eqalign{ 28 \cdot 52 x & = 28 \cdot (-1) \mod{97} \cr x & = -28 = 69 \mod{97} \quad\halmos \cr}$$

16. For what prime numbers p does p divide $2^p + 1$ ?

Suppose $p \mid 2^p + 1$ , i.e. $2^p + 1 = 0 \mod{p}$ .

$2 \notdiv 2^2 + 1$ , so $p = 2$ doesn't work.

Assume then that p is an odd prime. By Fermat's theorem, $2^p = 2 \mod{p}$ , so

$$2^p + 1 = 2 + 1 = 0 \mod{p}, \quad\hbox{or}\quad 3 = 0 \mod{p}.$$

This means that $p \mid 3$ . The only odd prime which divides 3 is $p = 3$ . Since $3 \mid 2^3 + 1$ , 3 works, and it's the only prime that works.

17. Solve $x^{38} - 3 x^{19} + 2 = 0 \mod{19}$ .

Note that 19 is prime. By Fermat's theorem, $x^{19} = x \mod{19}$ for any x. Therefore, $x^{38} = (x^{19})^2 = x^2 \mod{19}$ , and the equation becomes

$$x^2 - 3 x + 2 = 0 \mod{19}.$$

This gives $(x - 1)(x - 2) = 0 \mod{19}$ . Since 19 is prime, the only solutions are $x = 1 \mod{19}$ and $x = 2 \mod{19}$ .

18. (a) By making a table, find all solutions to

$$x^4 + 19 x + 12 = 0 \mod{11}.$$

(b) For each solution you found in (a), generate a solution to

$$x^4 + 19 x + 12 = 0 \mod{121}.$$

(Alternatively, show that this is not possible.)

(a)

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x \mod{11}$ & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^4 + 19 x + 12 \mod{11}$ & & 1 & & 10 & & 0 & & 7 & & 3 & & 6 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x \mod{11}$ & & 6 & & 7 & & 8 & & 9 & & 10 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^4 + 19 x + 12 \mod{11}$ & & 3 & & 5 & & 3 & & 1 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The solution is $x = 2$ .

(b) Let $f(x) = x^4 + 19 x + 12$ , so $f'(x) = 4 x^3 + 19$ . Then

$$f(2) = 66 \quad\hbox{and}\quad f'(2) = 51.$$

Note that $11 \notdiv 51$ . I have

$$51^{-1} = 7^{-1} = 8 \mod{11}.$$

Let

$$t = -f'(2)^{-1} \cdot \dfrac{f(2)}{11} = -8 \cdot \dfrac{66}{11} = -48 = 7 \mod{11}.$$

Then

$$2 + 11 \cdot t = 79.$$

This is a solution to $x^4 + 19 x + 12 = 0 \mod{121}$ .

19. Compute $\phi(2^3 \cdot 3^2 \cdot 5)$ .

$$\phi(2^3 \cdot 3^2 \cdot 5) = (2^3 \cdot 3^2 \cdot 5)\left(1 - \dfrac{1}{2}\right) \left(1 - \dfrac{1}{3}\right)\left(1 - \dfrac{1}{5}\right) = 96.\quad\halmos$$

20. Suppose $\phi(n) = n - 1$ . How many positive factors does n have?

Since $\phi(n) = n - 1$ , it follows that n is prime. Hence, it has 2 positive factors, namely 1 and n.

21. Suppose that $(n, 108) = 1$ . Prove that $n^{36} = 1 \mod{108}$ .

Note that

$$\phi(108) = 108\left(1 - \dfrac{1}{2}\right)\left(1 - \dfrac{1}{3}\right) = 36.$$

By Euler's Theorem, $n^{36} = 1 \mod{108}$ .

22. Reduce $107^{1002} \mod{100}$ to a number in the range $\{0, 1, \ldots, 99\}$ .

$$\phi(100) = 100 \left(1 - \dfrac{1}{2}\right) \left(1 - \dfrac{1}{5}\right) = 40.$$

Since $(100, 107) = 1$ , Euler's theorem implies that $107^{40} = 1 \mod{100}$ . Now

$$1002 = 40 \cdot 25 + 2.$$

Hence,

$$107^{1002} = (107^{40})^{25}\cdot 107^2 = 11449 = 49 \mod{100}.\quad\halmos$$

23. Prove that if $(n, 72) = 1$ , then $n^{12} = 1 \mod{72}$ .

Note that

$$\phi(72) = 72 \left(1 - \dfrac{1}{2}\right)\left(1 - \dfrac{1}{3}\right) = 24.$$

So applying Euler's theorem directly gives $n^{24} = 1 \mod{72}$ , which is not what I want.

Instead, I'll use the fact that if $a = b \mod{m}$ and $a = b \mod{n}$ and $(m, n) = 1$ , then $a = b \mod{mn}$ . Write $72 = 8 \cdot 9$ . Since $(n, 72) = 1$ , I also have $(n, 8) = 1$ and $(n, 9) = 1$ .

I have

$$\phi(8) = 8 - 4 = 4.$$

By Euler's theorem,

$$\eqalign{ n^4 & = 1 \mod{8} \cr (n^4)^3 & = 1^3 \mod{8} \cr n^{12} & = 1 \mod{8} \cr}$$

I have

$$\phi(9) = 9 - 3 = 6.$$

By Euler's theorem,

$$\eqalign{ n^6 & = 1 \mod{9} \cr (n^6)^2 & = 1^2 \mod{9} \cr n^{12} & = 1 \mod{9} \cr}$$

Since $n^{12} = 1 \mod{8}$ and $n^{12} = 1 \mod{9}$ , the result I cited above shows that $n^{12} = 1 \mod{72}$ .

24. Find the last three digits (units, tens, and hundreds) of $17^{40003}$ .

I need to find $17^{40003} \mod{1000}$ . Note that

$$\phi(1000) = 1000 \left(1 - \dfrac{1}{2}\right)\left(1 - \dfrac{1}{5}\right) = 400.$$

Since $(17, 1000) = 1$ , by Euler's Theorem,

$$17^{400} = 1 \mod{1000}.$$

Hence,

$$17^{40003} = (17^{400})^{100} \cdot 17^3 = 4913 = 913 \mod{1000}.$$

The last three digits are 913.

25. Compute $\phi(96)$ , $\mu(105)$ , $\sigma(108)$ , and $\tau(1000)$ .

Since $96 = 2^5 \cdot 3$ ,

$$\phi(96) = 96\left(1 - \dfrac{1}{2}\right) \left(1 - \dfrac{1}{3}\right) = 32.$$

Since $105 = 3 \cdot 5 \cdot 7$ , $mu(105) = (-1)^3 = -1$ .

Since $108 = 2^2 \cdot 3^3$ ,

$$\sigma(108) = \left(\dfrac{2^3 - 1}{2 - 1}\right) \left(\dfrac{3^4 - 1}{3 - 1}\right) = 280.$$

Since $1000 = 2^3 \cdot 5^3$ ,

$$\tau(1000) = (3 + 1)(3 + 1) = 16.\quad\halmos$$

26. What positive integers have exactly three positive divisors?

Suppose $\tau(n) = 3$ . Suppose the prime factorization of n is

$$n = p_1^{r_1} p_2^{r_2} \cdots p_k^{r_k}.$$

Then

$$3 = \tau(n) = (r_1 + 1)(r_2 + 1) \cdots (r_k + 1).$$

This is only possible if $k = 1$ and $r_1 + 1 = 3$ . This gives $r_1 = 2$ . Therefore, $n = p_1^2$ .

Therefore, the positive integers which have exactly three positive divisors are squares of primes.

27. Suppose that $\phi(m) = 32 n$ , where n is an odd number. Prove that m has no more than 5 different odd prime divisors.

Suppose $m = 2^r p_1^{r_1} p_2^{r_2} \cdots p_k^{r_k}$ , where the p's are distinct odd primes and the r's are greater than 0. Then

$$\phi(m) = (2^r - 2^{r-1})(p_1^{r_1} - p_1^{r_1-1}) (p_2^{r_2} - p_2^{r_2-1}) \cdots (p_k^{r_k} - p_k^{r_k-2}).$$

Now

$$p_i^{r_i} - p_i^{r_i-1} = p_i^{r_i-1}(p_i - 1).$$

Since $p_i$ is odd, $p_i - 1$ is even. Thus, each odd prime divisor of m contributes a factor of 2 to $\phi(m)$ . But $32 = 2^5$ is the largest power of 2 which divides $\phi(m)$ . Therefore, m can't have more than 5 different odd prime divisors.

28. Suppose that $\phi(n) = 28$ .

(a) Show that if p is a prime and $p \ge 31$ , then $p \notdiv n$ .

(b) Show that the largest power of 3 that can divide n is $3^1$ .

(c) Show that $7 \notdiv n$ .

(a) Suppose $p^r$ is the largest power of p which divides n, where $r \ge 1$ . Suppose also that $p \ge 31$ . Then

$$p^r - p^{r-1} = p^{r-1}(p - 1) \mid \phi(n) = 28.$$

But $p - 1 \ge 30$ , so $p^{r-1}(p - 1) \ge 30$ , and this is impossible. Hence, if p is a prime and $p \ge 31$ , then $p \notdiv n$ .

(b) Suppose $3^r$ is the largest power of 3 that divides n. Then

$$3^r - 3^{r-1} = 3^{r-1}(3 - 1) = 2 \cdot 3^{r-1} \mid \phi(n) = 28.$$

If $r > 1$ , then $3 \mid 3^{r-1} \mid 28$ , which is a contradiction. Hence, $r \le 1$ , and the largest power of 3 that can divide n is $3^1$ .

(c) Suppose that $7^r$ is the largest power of 7 that divides n. Then

$$7^r - 7^{r-1} = 7^{r-1}(7 - 1) = 6 \cdot 7^{r-1} \mid \phi(n) = 28.$$

This is a contradiction, since $6 \notdiv 28$ . Therefore, $7 \notdiv n$ .

29. Let n be the square of an odd integer. Prove that $\sigma(n)$ is odd.

Let $n = m^2$ , where m is odd. Then n is odd, so the factors of n other than m occur in pairs a, b, where $ab = n$ , $a \ne b$ , and a and b are odd. Hence, $a + b$ is even, and the sum of the factors of n other than m is a sum of even numbers. Therefore,

$$\sigma(n) = (\hbox{sum of evens}) + m = (\hbox{even}) + (\hbox{odd}) = (\hbox{odd}).\quad\halmos$$

30. Find all positive integers n such that $\sigma(n) = n + 7$ .

Suppose $\sigma(n) = n + 7$ . I may assume $n > 1$ , since $\sigma(1) = 1 \ne 1 + 7$ . Thus, 1 and n are distinct divisors of n. Let d be the sum of the divisors of n other than 1 or n. Then

$$n + 7 = \sigma(n) = 1 + n + d, \quad\hbox{so}\quad d = 6.$$

If the largest divisor in d is 6, then n is divisible by 2 and 3 as well. This gives $6 = d \ge 6 + 3 + 2$ , which is a contradiction.

If the largest divisor in d is 5, then $6 = d = 5 + s$ , where s is the sum of the other terms in d. But then $s = 1$ , and 1 can't be one of the divisors in d. This is a contradiction.

If the largest divisor in d is 4, then 2 is also a divisor of n. This is possible, since $6 = d = 2 + 4$ . In this case, the divisors of n are 1, 2, 4, and n, so $n = 8$ . This works, since $\sigma(8) = 15 = 8 + 7$ .

If the largest divisor in d is 3, then $6 = d = 3 + s$ , where s is the sum of the other terms in d. But then $s = 3$ , for which the only possibilities are 3 and $1 + 2$ . The first is ruled out, because 3 was already accounted for; the second is ruled out, because d does not include 1. Hence, this is a contradiction.

The largest divisor in d can't be 2, because there is no way to write 6 as a sum of 2 and integers less than 2 and bigger than 1.

Therefore, the only positive integer n such that $\sigma(n) = n + 7$ is $n = 8$ .

31. For what integers $n \ge 1$ is $\tau(n)$ an odd number?

First, $\tau(1) = 1$ is odd.

Factors of n come in pairs: $n = a \cdot b$ . Each such pair contributes two factors, provided that $a \ne b$ . Hence, then number of factors must be even, unless $n = a^2$ for some a.

Thus, $\tau(n)$ is odd exactly when n is a perfect square.

32. Let p be prime. Show that $\dfrac{\phi(p) \cdot \sigma(p) + 1}{p} = p$ .

$$\eqalign{ \phi(p) \cdot \sigma(p) + 1 & = (p - 1)(p + 1) + 1 \cr & = p^2 - 1 + 1 \cr & = p^2 \cr}$$

Hence, $\dfrac{\phi(p) \cdot \sigma(p) + 1}{p} = p$ .

33. Give a set of infinitely many integers n such that $18 \mid \phi(n)$ .

If $19 \mid n$ , then $18 = 19 - 1 \mid \phi(n)$ . Thus, all of the integers in the following set satisfy $18 \mid \phi(n)$ :

$$19, \quad 38, \quad 57, \quad \ldots, 19 n, \ldots .\quad\halmos$$

34. Prove that if $\phi(n) \mid n - 1$ , then n is square-free --- that is, there is no prime p such that $p^2 \mid n$ .

Suppose that $\phi(n) \mid n - 1$ , but $p^2 \mid n$ , where p is prime. Then

$$p \mid p^2 - p \mid \phi(n) \mid n - 1.$$

Since $p \mid p^2 \mid n$ as well, I have $p \mid (n, n - 1)$ .

However,

$$(n, n - 1) = (n - (n - 1), n - 1) = (1, n - 1) = 1.$$

This is a contradiction. Hence, there is no prime p such that $p^2 \mid n$ .

35. Find all positive integers n satisfying $7 \mid n$ and $\phi(n) = 18$ .

Suppose that $\phi(n) = 18$ .

The formula for $\phi(n)$ in terms of the prime factorization of n implies that if p is prime and $p \mid n$ , then $p - 1 \mid \phi(n)$ .

First, if p is prime and $p > 19$ , then $p - 1 > 18$ , so $p - 1 \notdiv \phi(n)$ . Hence, $p \notdiv n$ . Thus, n can only be divisible by primes from 2 through 19.

If $5 \mid n$ , then $4 = 5 - 1 \mid \phi(n)$ , which is impossible for $\phi(n) = 18$ . Hence, $5 \notdiv n$ .

If $11 \mid n$ , then $10 = 11 - 1 \mid \phi(n)$ , which is impossible for $\phi(n) = 18$ . Hence, $11 \notdiv n$ .

If $13 \mid n$ , then $12 = 13 - 1 \mid \phi(n)$ , which is impossible for $\phi(n) = 18$ . Hence, $13 \notdiv n$ .

If $17 \mid n$ , then $16 = 17 - 1 \mid \phi(n)$ , which is impossible for $\phi(n) = 18$ . Hence, $17 \notdiv n$ .

At this point, I may suppose that the prime factorization of n is

$$n = 2^a \cdot 3^b \cdot 7^c \cdot 19^d.$$

In this expression, a, b, and d may be zero, but I know that $c \ge 1$ . So I have

$$18 = \phi(n) = (2^a - 2^{a-1})(3^b - 3^{b-1})(7^c - 7^{c-1})(19^d - 19^{d-1}) =$$

$$(2^a - 2^{a-1})(3^b - 3^{b-1})7^{c-1}(7 - 1)(19^d - 19^{d-1}) = 6 \cdot 7^{c-1}(2^a - 2^{a-1})(3^b - 3^{b-1})(19^d - 19^{d-1}).$$

Hence,

$$3 = 7^{c-1} (2^a - 2^{a-1})(3^b - 3^{b-1})(19^d - 19^{d-1}).$$

If $c \ge 2$ , then $c - 1 \ge 1$ , and $7 \mid 7^{c-1}$ . This is impossible, since the left side is equal to 3. Hence, $c = 1$ .

If $d \ge 1$ , then

$$19^d - 19^{d-1} = 19^{d-1}(19 - 1) = 19^{d-1} \cdot 18.$$

This is impossible, since the left side is equal to 3. Hence, $d = 0$ .

Now I have

$$n = 2^a \cdot 3^b \cdot 7.$$

Consequently,

$$18 = \phi(n) = (2^a - 2^{a-1})(3^b - 3^{b-1})(6), \quad\hbox{so}\quad 3 = (2^a - 2^{a-1})(3^b - 3^{b-1}).$$

If $b \ge 1$ , then

$$3^b - 3^{b-1} = 3^{b-1}(3 - 1) = 3^{b-1} \cdot 2.$$

This is impossible, since the left side of the previous equation is 3. Therefore, $b = 0$ .

But now I have $3 = 2^a - 2^{a-1}$ , and no $a \ge 0$ will make this true.

Having ruled out all possibilities, I conclude that there are no positive integers n satisfying $7 \mid n$ and $\phi(n) = 18$ .

36. In each case, if the function is multiplicative, prove it; if it is not, give a specific counterexample.

(a) $f: \integer^+ \to \real$ given by

$$f(x) = x + 1.$$

(b) $g: \integer^+ \to \real$ given by

$$g(x) = \sqrt{x}.$$

(a) $(4, 7) = 1$ , but

$$f(4 \cdot 7) = f(28) = 28 + 1 = 29 \quad\hbox{while}\quad f(4) \cdot f(7) = (4 + 1)(7 + 1) = 40.$$

Hence, f is not multiplicative.

(b)

$$g(x y) = \sqrt{x y} = \sqrt{x} \cdot \sqrt{y} = g(x) \cdot g(y).$$

Hence, g is multiplicative --- in fact, completely multiplicative.

37. Let $D f$ denote the divisor sum of the arithmetic function f. Suppose $f(x) = x^2$ . Compute $(D f)(10)$ .

$$(D f)(10) = \sum_{d \mid 10} f(d) = f(1) + f(2) + f(5) + f(10) = 1^2 + 2^2 + 5^2 + 10^2 = 130.\quad\halmos$$

38. Find $(2^{36} - 1, 2^{42} - 1)$ .

If a and b are positive integers, then

$$(2^a - 1, 2^b - 1) = 2^{(a, b)} - 1.$$

Thus,

$$(2^{36} - 1, 2^{42} - 1) = 2^{(36, 42)} - 1 = 2^6 - 1 = 63.\quad\halmos$$

39. Find a proper factor of $2^{29} - 1$ .

A prime factor of $2^{29} - 1 = 536870911$ must have the form $58 k + 1$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & k & & $58 k+1$ & & Result & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 59 & & $59\notdiv 536870911$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 117 & & 117 isn't prime & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 3 & & 175 & & 175 isn't prime & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 4 & & 233 & & $233\mid 536870911$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

233 is a proper factor of $2^{29} - 1$ .

Change is not made without inconvenience, even from worse to better. - Richard Hooker

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga