Review Problems for Test 3

Math 393

These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the absence of a topic does not imply that it won't appear on the test.

1. Find the decoding transformation for the affine transformation cipher

$$C = 15 P + 7 \mod{26}.$$

2. Find the decoding transformation for the digraphic cipher

$$\left[\matrix{C_1 \cr C_2 \cr}\right] = \left[\matrix{7 & 5 \cr 5 & 10 \cr}\right] \left[\matrix{P_1 \cr P_2 \cr}\right] \mod{26}.$$

3. Calvin Butterball constructs the following digraphic cipher:

$$\left[\matrix{C_1 \cr C_2 \cr}\right] = \left[\matrix{7 & 4 \cr 2 & 3 \cr}\right] \left[\matrix{P_1 \cr P_2 \cr}\right] \mod{26}.$$

Show that this is a bad idea by finding two different plaintext blocks that give the same ciphertext block.

4. Find the decoding transformation for the exponential cipher

$$C = P^{23} \mod{5003}.$$

5. Suppose that $n = 80609$ is a product of two primes p and q, and that $\phi(n) = 79920$ . Without factoring n directly, find p and q.

6. (a) Use an RSA cipher with $n = 4141 = 41 \cdot 101$ and exponent 27 to encipher the word OMELET.

(b) Find the decoding transformation for the cipher in part (a).

7. Find a solution to the following quadratic congruence.

$$x^2 = 280 \mod{529}.$$

(Note that $529 = 23^2$ .)

8. Solve $x^2 = 33 \mod{527}$ . [Note: $527 = 17 \cdot 31$ .]

9. Find the quadratic residues mod 17.

10. Find the quadratic residues mod 18.

11. Compute the following Legendre symbols:

(a) $\legendre{71}{79}$ .

(b) $\legendre{72}{79}$ .

(c) $\legendre{564}{569}$ .

(d) $\legendre{5}{55 k + 1}$ , if $55 k + 1$ is prime.

(e) Compute $\legendre{8}{31}$ .

12. Determine whether $x^2 = 1220 \mod{1301}$ has solutions. (Note: 1301 is prime.)

13. State the Law of Quadratic Reciprocity in terms of congruences, and in terms of Legendre symbols.

14. Show that if p is an odd prime and 2, 3, and 6 are distinct mod p, then at least one of 2, 3, or 6 is a quadratic residue mod p.

15. Use Gauss's lemma to determine whether $x^2 = 15 \mod{17}$ has any solutions.

16. Compute the following Jacobi symbols.

(a) $\legendre{37}{297}$ .

(b) $\legendre{175}{213}$ .

17. Let p be an odd prime. Prove that

$$\legendre{-2}{p} = \cases{ 1 & if $p = 8 k + 1$ or $p = 8 k + 3$ \cr -1 & if $p = 8 k + 5$ or $p = 8 k + 7$ \cr}.$$

18. Convert $(7213)_8$ to base 10.

19. Convert 1808 to base 7.

20. Express 0.3 in base-7.

21. Express $(0.54242\ldots)_6 = (0.5 \overline{42})_6$ as a decimal fraction in lowest terms.

22. Let b be a positive integer greater than 3. Express $(0.3(b - 1)3(b - 1) \ldots)_b = (0.\overline{3(b - 1)})_b$ as a rational function of b.

23. Let b be a positive integer greater than 3. Find the base b expansion of $\dfrac{2 b^2 + 1}{b^2 - 1}$ .

24. Find the finite continued fraction expansion for $\dfrac{983}{237}$ .

25. Find the successive convergents and the exact value of the finite continued fraction $[3, 1, 4, 1, 1, 6]$ .

26. Suppose x is a positive integer. Find the exact value of

$$1 + \dfrac{1}{x + \dfrac{1}{x^2 + \dfrac{1}{x^3}}}.$$

27. Use continued fractions to find an integer linear combination of 501 and 113 which is equal to 1.

Solutions to the Review Problems for Test 3

1. Find the decoding transformation for the affine transformation cipher

$$C = 15 P + 7 \mod{26}.$$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 26 & & - & & 7 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 15 & & 1 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 11 & & 1 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 4 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 3 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 3 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$1 = (-4)(26) + (7)(15), \quad\hbox{so}\quad 7 = 15^{-1} \mod{26}.$$

Therefore,

$$\eqalign{C & = 15 P + 7 \mod{26} \cr C - 7 & = 15 P \mod{26} \cr C + 19 & = 15 P \mod{26} \cr 7(C + 19) & = P \mod{26} \cr 7 C + 3 & = P \mod{26} \cr}\quad\halmos$$

2. Find the decoding transformation for the digraphic cipher

$$\left[\matrix{C_1 \cr C_2 \cr}\right] = \left[\matrix{7 & 5 \cr 5 & 10 \cr}\right] \left[\matrix{P_1 \cr P_2 \cr}\right] \mod{26}.$$

Find the inverse of the matrix:

$$\left[\matrix{7 & 5 \cr 5 & 10 \cr}\right]^{-1} = (7 \cdot 10 - 5 \cdot 5)^{-1} \left[\matrix{10 & -5 \cr -5 & 7 \cr}\right] = 45^{-1}\cdot \left[\matrix{10 & -5 \cr -5 & 7 \cr}\right] \mod{26}.$$

Use the Euclidean algorithm to compute $45^{-1} \mod{26}$ :

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 45 & & - & & 19 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 26 & & 1 & & 11 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 19 & & 1 & & 8 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 7 & & 2 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 5 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus,

$$(11)(45) + (-19)(26) = 1, \quad\hbox{so}\quad (11)(45) = 1 \mod{26}.$$

Therefore, $45^{-1} = 11 \mod{26}$ , and the inverse matrix is

$$11 \cdot \left[\matrix{10 & -5 \cr -5 & 7 \cr}\right] = \left[\matrix{110 & -55 \cr -55 & 77 \cr}\right] = \left[\matrix{6 & 23 \cr 23 & 25 \cr}\right] \mod{26}.$$

The decoding transformation is

$$\left[\matrix{P_1 \cr P_2 \cr}\right] = \left[\matrix{6 & 23 \cr 23 & 25 \cr}\right] \left[\matrix{C_1 \cr C_2 \cr}\right] \mod{26}.\quad\halmos$$

3. Calvin Butterball constructs the following digraphic cipher:

$$\left[\matrix{C_1 \cr C_2 \cr}\right] = \left[\matrix{7 & 4 \cr 2 & 3 \cr}\right] \left[\matrix{P_1 \cr P_2 \cr}\right] \mod{26}.$$

Show that this is a bad idea by finding two different plaintext blocks that give the same ciphertext block.

The problem, of course, is that

$$\left|\matrix{7 & 4 \cr 2 & 3 \cr}\right| = 13 \quad\hbox{and}\quad (13, 26) = 13 \ne 1.$$

I want $P_1$ , $P_2$ , $P_1'$ , $P_2'$ , such that $(P_1, P_2) \ne (P_1', P_2')$ , but

$$\left[\matrix{7 & 4 \cr 2 & 3 \cr}\right] \left[\matrix{P_1 \cr P_2 \cr}\right] = \left[\matrix{7 & 4 \cr 2 & 3 \cr}\right] \left[\matrix{P_1' \cr P_2' \cr}\right] \mod{26}.$$

Moving all the terms to the left side and factoring, I have

$$\left[\matrix{7 & 4 \cr 2 & 3 \cr}\right] \left[\matrix{P_1 - P_1' \cr P_2 - P_2' \cr}\right] = \left[\matrix{0 \cr 0 \cr}\right] \mod{26}.$$

I see that what I need is a nontrivial (i.e. nonzero) solution to the homogeneous system

$$\left[\matrix{7 & 4 \cr 2 & 3 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{0 \cr 0 \cr}\right] \mod{26}.$$

To do this, row reduce. To find out how to "divide" the first row by 7, use the Extended Euclidean Algorithm:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 26 & & - & & 11 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 7 & & 3 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 5 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\eqalign{ 1 & = (26, 7) = 26 \cdot 3 + 7 \cdot (-11) \cr 1 & = 7 \cdot (-11) \mod{26} \cr 1 & = 7 \cdot 15 \mod{25} \cr}$$

Thus,

$$\left[\matrix{7 & 4 \cr 2 & 3 \cr}\right] \matrix{\to \cr r_1 \to 15 r_1 \cr} \left[\matrix{1 & 8 \cr 2 & 3 \cr}\right] \matrix{\to \cr r_2 \to r_2 + 24 r_1 \cr} \left[\matrix{1 & 8 \cr 0 & 13 \cr}\right] \mod{26}.$$

I can't go any further, because 13 isn't invertible mod 26.

These equations say

$$\eqalign{ x + 8 y & = 0 \mod{26} \cr 13 y & = 0 \mod{26} \cr}$$

I want a nonzero solution. So take $y = 2$ to satisfy the second equation. (Any even number will work for y.) Plugging this into the first equation, I get

$$x + 16 = 0, \quad\hbox{or}\quad x = 10.$$

Finally, recall that $(x, y)$ represents $(P_1 - P_1', P_2 - P_2')$ . So to get two different plaintexts that give the same ciphertext, set $(P_1', P_2')$ to anything --- say $(0, 0)$ --- and add $(10, 2)$ to get $(P_1, P_2) = (10, 2)$ .

You can check that

$$\left[\matrix{7 & 4 \cr 2 & 3 \cr}\right] \left[\matrix{P_1 \cr P_2 \cr}\right] = \left[\matrix{0 \cr 0 \cr}\right] \mod{26} \quad\hbox{and}\quad \left[\matrix{7 & 4 \cr 2 & 3 \cr}\right] \left[\matrix{P_1' \cr P_2' \cr}\right] = \left[\matrix{0 \cr 0 \cr}\right] \mod{26}.$$

Try setting $(P_1', P_2') = (1, 5)$ (say), so $(P_1, P_2) = (10 + 1, 5 + 2) = (11, 7)$ . You can verify for yourself that this choice of $(P_1, P_2)$ and $(P_1', P_2')$ will work as well.

4. Find the decoding transformation for the exponential cipher

$$C = P^{23} \mod{5003}.$$

I need to find $23^{-1} \mod{5002}$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 5002 & & - & & 435 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 23 & & 217 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 11 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 11 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\eqalign{ 435 \cdot 23 - 2 \cdot 5002 & = 1 \cr 435 \cdot 23 & = 1 \mod{5002} \cr}$$

$23^{-1} = 435 \mod{5002}$ , so the decoding transformation is

$$P = C^{435} \mod{5003}.\quad\halmos$$

Note: The inverse must be converted to a positive number before being used as the exponent in the decoding transformation. For example, if the original exponent had been 19, then

$$19^{-1} = -1053 = 3949 \mod{5002}.$$

The decoding transformation would then be $P = C^{3949} \mod{5003}$ .

5. Suppose that $n = 80609$ is a product of two primes p and q, and that $\phi(n) = 79920$ . Without factoring n directly, find p and q.

I have

$$\phi(n) = \phi(pq) = (p - 1)(q - 1) = n - (p + q) + 1, \quad\hbox{so}\quad p + q = n - \phi(n) + 1.$$

Thus,

$$p + q = 80609 - 79920 + 1 = 690.$$

In addition,

$$p - q = \sqrt{(p + q)^2 - 4 pq} = \sqrt{(p + q)^2 - 4 n}.$$

Therefore,

$$p - q = \sqrt{690^2 - 4 \cdot 80609} = 392.$$

So

$$2 p = (p + q) + (p - q) = 1082, \quad\hbox{and}\quad p = 541.$$

Hence, $q = 690 - 541 = 149$ . The primes are 149 and 541.

6. (a) Use an RSA cipher with $n = 4141 = 41 \cdot 101$ and exponent 27 to encipher the word OMELET.

(b) Find the decoding transformation for the cipher in part (a).

(a) Note that $\phi(4141) = 40 \cdot 100 = 4000$ , and $(27, 4000) = 1$ .

since $2525 < 4141 < 252525$ , I use blocks of 2 letters.

Translate OMELET to 1412 0411 0419. To encipher the first block, for example, I compute

$$1412^{27} = 1677 \mod{4141}.$$

Proceeding in the same way, I obtain the ciphertext 1677 0288 1139.

(b) I need to find d such that $d \cdot 27 = 1 \mod{4000}$ . Use the Euclidean algorithm:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 4000 & & - & & 1037 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 27 & & 148 & & 7 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 4 & & 6 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 3 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 3 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

This means that

$$(7)(4000) + (-1037)(27) = 1, \quad\hbox{or}\quad (-1037)(27) = 1 \mod{4000}.$$

Since $-1037 = 2963 \mod{4000}$ , I can take $d = 2963$ . The decoding transformation is

$$P = C^{2963} \mod{4141}.\quad\halmos$$

7. Find a solution to the following quadratic congruence.

$$x^2 = 280 \mod{529}.$$

(Note that $529 = 23^2$ .)

First, consider the congruence mod 23:

$$x^2 = 280 = 4 \mod{23}.$$

Clearly, $x = 2$ is a solution.

I'll try to find a solution $y = 2 + 23 z$ to the original congruence:

$$\eqalign{ y^2 & = 280 \mod{529} \cr (2 + 23 z)^2 & = 280 \mod{529} \cr 4 + 92 z + 529 z^2 & = 280 \mod{529} \cr 92 z & = 276 \mod{529} \cr}$$

Note that $276 = 3 \cdot 92$ . Dividing the congruence by 92, I must divide the modulus by $(529, 92) = 23$ :

$$z = 3 \mod{23}.$$

Then a solution is given by

$$y = 2 + 23 \cdot 3 = 71 \mod{529}.$$

Note that $y = -71 = 458 \mod{529}$ also works.

8. Solve $x^2 = 33 \mod{527}$ .

$527 = 17 \cdot 31$ , so this is equivalent to solving

$$x^2 = 33 \mod{17} \quad\hbox{and}\quad x^2 = 33 \mod{31}.$$

$x^2 = 33 \mod{17}$ becomes $x^2 = 16 \mod{17}$ , which has solutions $x = \pm 4 \mod{17}$ .

$x^2 = 33 \mod{31}$ becomes $x^2 = 2 \mod{31}$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & & 7 & & 8 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 \mod{31}$ & & 1 & & 4 & & 9 & & 16 & & 25 & & 5 & & 18 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 9 & & 10 & & 11 & & 12 & & 13 & & 14 & & 15 & & & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 \mod{31}$ & & 19 & & 7 & & 28 & & 20 & & 14 & & 10 & & 8 & & & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

(I obviously don't need to check $x = 0$ , and the squares from 16 to 30 repeat those from 1 to 15, backwards.)

The solutions are $x = \pm 8 \mod{31}$ .

Now take cases. If $x = 4 \mod {17}$ and $x = 8 \mod{31}$ , then

$$\eqalign{x & = 4 + 17 a \cr 4 + 17 a & = 8 \mod{31} \cr 17 a & = 4 \mod{31} \cr}$$

I need to find $17^{-1} \mod{31}$ . Use the Extended Euclidean Algorithm:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 31 & & - & & 11 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 17 & & 1 & & 6 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 14 & & 1 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 3 & & 4 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$1 = 11 \cdot 17 - 6 \cdot 31, \quad 1 = 11 \cdot 17 \mod{31}.$$

Thus, $17^{-1} = 11 \mod{31}$ . So

$$\eqalign{11 \cdot 17 a & = 11 \cdot 4 \mod{31} \cr a & = 44 = 13 \mod{31} \cr a & = 13 + 31 b \cr x & = 4 + 17(13 + 31 b) \cr x & = 225 \mod{527} \cr}$$

If $x = 4 \mod {17}$ and $x = -8 = 23 \mod{31}$ , then

$$\eqalign{x & = 4 + 17 a \cr 4 + 17 a & = 23 \mod{31} \cr 17 a & = 19 \mod{31} \cr 11 \cdot 17 a & = 11 \cdot 19 \mod{31} \cr a & = 209 = 23 \mod{31} \cr a & = 23 + 31 b \cr x & = 4 + 17(23 + 31 b) \cr x & = 395 \mod{527} \cr}$$

The other solutions are $x = -225 = 302 \mod{527}$ and $x = -395 = 132 \mod{527}$ .

All together, the solutions are $x = 132, 225, 302, 395 \mod{527}$ .

9. Find the quadratic residues mod 17.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & & 7 & & 8 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 \mod{17}$ & & 1 & & 4 & & 9 & & 16 & & 8 & & 2 & & 15 & & 13 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 9 & & 10 & & 11 & & 12 & & 13 & & 14 & & 15 & & 16 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 \mod{17}$ & & 13 & & 15 & & 2 & & 8 & & 16 & & 9 & & 4 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The quadratic residues mod 17 are 1, 2, 4, 8, 9, 13, 15, and 16.

10. Find the quadratic residues mod 18.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & & 7 & & 8 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 \mod{18}$ & & 0 & & 1 & & 4 & & 9 & & 16 & & 7 & & 0 & & 13 & & 10 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 9 & & 10 & & 11 & & 12 & & 13 & & 14 & & 15 & & 16 & & 17 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 \mod{18}$ & & 9 & & 10 & & 13 & & 0 & & 7 & & 16 & & 9 & & 4 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Of the squares mod 18, only 1, 7, and 13 are relatively prime to 18. So the quadratic residues mod 18 are 1, 7, and 13.

11. Compute the following Legendre symbols:

(a) $\legendre{71}{79}$ .

(b) $\legendre{72}{79}$ .

(c) $\legendre{564}{569}$ .

(d) $\legendre{5}{55 k + 1}$ , if $55 k + 1$ is prime.

(e) $\legendre{8}{31}$ .

(a) Since $71 = 4 \cdot 17 + 3$ and $79 = 4 \cdot 19 + 3$ , reciprocity gives

$$\legendre{71}{79} = -\legendre{79}{71} = -\legendre{8}{71} = -\legendre{2}{71}\cdot \legendre{4}{71} = -\legendre{2}{71}\cdot 1 = -\legendre{2}{71}.$$

Now if p is an odd prime,

$$\legendre{2}{p} = (-1)^{(p^2-1)/8}.$$

So

$$\legendre{2}{71} = (-1)^{(71^2-1)/8} = (-1)^{630} = 1.$$

Hence, $\legendre{71}{79} = -1$ .

(b)

$$\legendre{72}{79} = \legendre{36}{79}\cdot \legendre{2}{79} = 1 \cdot \legendre{2}{79} = \legendre{2}{79}.$$

As in (a),

$$\legendre{2}{79} = (-1)^{(79^2-1)/8} = (-1)^{780} = 1.$$

Thus, $\legendre{72}{79} = 1$ .

(c) 569 is prime.

$564 = 3 \cdot 4 \cdot 47$ , so

$$\legendre{564}{569} = \legendre{3}{569}\legendre{4}{569} \legendre{47}{569}.$$

$\legendre{4}{569} = 1$ , because 4 is a perfect square.

$569 = 4 \cdot 142 + 1$ , so

$$\legendre{3}{569} = \legendre{569}{3} = \legendre{2}{3} = -1,$$

$$\legendre{47}{569} = \legendre{569}{47} = \legendre{5}{47} = \legendre{47}{5} = \legendre{2}{5} = -1.$$

Therefore,

$$\legendre{564}{569} = (-1)(1)(-1) = 1.\quad\halmos$$

(d) Since $5 = 4 \cdot 1 + 1$ , Quadratic Reciprocity gives

$$\legendre{5}{55 k + 1} = \legendre{55 k + 1}{5} = \legendre{1}{5} = 1.\quad\halmos$$

(e)

$$\legendre{8}{31} = \legendre{4}{31} \legendre{2}{31} = 1 \cdot \legendre{2}{31} = (-1)^{(31^2 - 1)/8} = (-1)^{120} = 1.$$

To compute $\legendre{2}{31}$ , I used the formula $\legendre{2}{p} = (-1)^{(p^2 - 1)/8}$ . You could also compute the last symbol using Euler's Theorem.

12. Determine whether $x^2 = 1220 \mod{1301}$ has solutions. (Note: 1301 is prime.)

$$\legendre{1220}{1301} = \legendre{4}{1301} \legendre{5}{1301} \legendre{61}{1301} = \legendre{5}{1301} \legendre{61}{1301} = \legendre{1301}{5} \legendre{1301}{61} = \legendre{1}{5} \legendre{20}{61} =$$

$$\legendre{4}{61} \legendre{5}{61} = \legendre{5}{61} = \legendre{61}{5} = \legendre{1}{5} = 1.$$

Hence, $x^2 = 1220 \mod{1301}$ has solutions.

13. State the Law of Quadratic Reciprocity in terms of congruences, and in terms of Legendre symbols.

Let p and q be distinct odd primes.

In terms of congruences, reciprocity says: Consider the congruences

$$x^2 = p \mod{q} \quad\hbox{and}\quad x^2 = q \mod{p}.$$

If either p or q has the form $4 k + 1$ for $k \in \natural$ , then both congruences have solutions or both do not have solutions.

If both $p = 4 j + 3$ and $q = 4 k + 3$ for $j, k \in \natural$ , then one congruence is solvable and the other is not.

In terms of Legendre symbols, reciprocity says:

$$\legendre{p}{q} \legendre{q}{p} = (-1)^{[(p^2-1)/2][(q^2-1)/2]}.$$

An equivalent statement in terms of symbols is this: If either p or q has the form $4 k + 1$ for $k \in \natural$ , then $\legendre{p}{q} = \legendre{q}{p}$ .

If both $p = 4 j + 3$ and $q = 4 k + 3$ for $j, k \in \natural$ , then $\legendre{p}{q} = -\legendre{q}{p}$ .

14. Show that if p is an odd prime and 2, 3, and 6 are distinct mod p, then at least one of 2, 3, or 6 is a quadratic residue mod p.

I have

$$\legendre{6}{p} = \legendre{2}{p} \legendre{3}{p}.$$

Suppose 2, 3, and 6 are quadratic nonresidues mod p. Then all three of the symbols $\legendre{6}{p}$ , $\legendre{2}{p}$ , and $\legendre{3}{p}$ are -1, and the equation above says "$-1 = (-1)(-1)$ ", a contradiction. Hence, at least one of the three is a quadratic residue mod p.

15. Use Gauss's lemma to determine whether $x^2 = 15 \mod{17}$ has any solutions.

Gauss's lemma applies, since $(15, 17) = 1$ . $\dfrac{17 - 1}{2} = 8$ , so I compute the first 8 multiples of 15 mod 17:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & k & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & & 7 & & 8 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $15 k\mod{17}$ & & 15 & & 13 & & 11 & & 9 & & 7 & & 5 & & 3 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Now $\dfrac{17}{2} = 8.5$ , and 4 of these residues are greater than 8.5. By Gauss's lemma,

$$\legendre{15}{17} = (-1)^4 = 1.$$

Therefore, $x^2 = 15 \mod{17}$ has solutions.

16. Compute the following Jacobi symbols.

(a) $\legendre{37}{297}$ .

(b) $\legendre{175}{213}$ .

(a)

$$\legendre{37}{297} = \legendre{37}{9 \cdot 33} = \legendre{37}{33} = \legendre{4}{37} = 1.\quad\halmos$$

(b) By direct computation 3 isn't a square mod 7, so

$$\legendre{175}{213} = \legendre{7 \cdot 25}{213} = \legendre{7}{213} = \legendre{213}{7} = \legendre{3}{7} = -1.\quad\halmos$$

17. Let p be an odd prime. Prove that

$$\legendre{-2}{p} = \cases{ 1 & if $p = 8 k + 1$ or $p = 8 k + 3$ \cr -1 & if $p = 8 k + 5$ or $p = 8 k + 7$ \cr}.$$

Note for all four cases that

$$\legendre{-2}{p} = \legendre{-1}{p} \legendre{2}{p} = (-1)^{(p - 1)/2} \cdot (-1)^{(p^2 - 1)/8}.$$

If $p = 8 k + 1$ , then

$$\eqalign{ \dfrac{p - 1}{2} & = \dfrac{8 k}{2} = 4 k \cr (-1)^(-1)^{(p - 1)/2} & = (-1)^{4 k} = 1 \cr}$$

$$\eqalign{ \dfrac{p^2 - 1}{8} & = \dfrac{64 k^2 + 16 k}{8} = 8 k^2 + 2 k \cr (-1)^{(p^2 - 1)/8} & = 1 \cr}$$

Hence, $\legendre{-2}{p} = 1 \cdot 1 = 1$ .

If $p = 8 k + 3$ , then

$$\eqalign{ \dfrac{p - 1}{2} & = \dfrac{8 k + 2}{2} = 4 k + 1 \cr (-1)^(-1)^{(p - 1)/2} & = -1 \cr}$$

$$\eqalign{ \dfrac{p^2 - 1}{8} & = \dfrac{64 k^2 + 48 k + 8}{8} = 8 k^2 + 6 k + 1 \cr (-1)^{(p^2 - 1)/8} & = -1 \cr}$$

Hence, $\legendre{-2}{p} = (-1) \cdot (-1) = 1$ .

If $p = 8 k + 5$ , then

$$\eqalign{ \dfrac{p - 1}{2} & = \dfrac{8 k + 4}{2} = 4 k + 2 \cr (-1)^(-1)^{(p - 1)/2} & = 1 \cr}$$

$$\eqalign{ \dfrac{p^2 - 1}{8} & = \dfrac{64 k^2 + 80 k + 24}{8} = 8 k^2 + 10 k + 3 \cr (-1)^{(p^2 - 1)/8} & = -1 \cr}$$

Hence, $\legendre{-2}{p} = 1 \cdot (-1) = -1$ .

If $p = 8 k + 7$ , then

$$\eqalign{ \dfrac{p - 1}{2} & = \dfrac{8 k + 6}{2} = 4 k + 3 \cr (-1)^(-1)^{(p - 1)/2} & = -1 \cr}$$

$$\eqalign{ \dfrac{p^2 - 1}{8} & = \dfrac{64 k^2 + 112 k + 48}{8} = 8 k^2 + 14 k + 6 \cr (-1)^{(p^2 - 1)/8} & = 1 \cr}$$

Hence, $\legendre{-2}{p} = (-1) \cdot 1 = -1$ .

18. Convert $(7213)_8$ to base 10.

Note that

$$(7123)_8 = 7 \cdot 8^3 + 1 \cdot 8^2 + 2 \cdot 8 + 3.$$

Thus, I need to plug $x = 8$ into the polynomial $7 x^3 + x^2 + 2 x + 3$ . I can do this, for instance, using synthetic division (Horner's method):

$$\hbox{\epsfysize=0.75in \epsffile{rev3-1.eps}}$$

Hence, $(7213)_8 = 3723$ .

19. Convert 1808 to base 7.

I can do this by successive division by 7:

$$\hbox{\epsfysize=0.5in \epsffile{rev3-2.eps}}$$

To see why this works, suppose that

$$1808 = a_3 \cdot 7^3 + a_2 \cdot 7^2 + a_1 \cdot 7 + a_0.$$

Rewrite the right side using Horner's method:

$$1808 = ((a_3 \cdot 7 + a_2) \cdot 7 + a_1) \cdot 7 + a_0.$$

$a_0$ is the remainder when 1808 is divided by 7. The quotient is $(a_3 \cdot 7 + a_2) \cdot 7 + a_1$ ; if I divide this quotient by 7, the remainder is $a_1$ . And so on.

Thus, $1808 = (5162)_7$ .

20. Express 0.3 in base-7.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & a & & x & & $7 x$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & - & & 0.3 & & 2.1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 0.1 & & 0.7 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 0 & & 0.7 & & 4.9 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 4 & & 0.9 & & 6.3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 6 & & 0.3 & & 2.1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

For example, in the first row I multiplied 0.3 by the base 7 to get 2.1. I took the integer part of 2.1, which is 2, and put it in the first spot in the second row. Then $2.1 - 2 = 0.1$ , and that goes into the second spot in the second row. Then I just repeat the process: $7 \cdot 0.1 = 0.7$ , the integer part of 0.7 is 0, subtracting gives $0.7 - 0 = 0.7$ , and so on. I keep going until the numbers repeat, at which point I have the expansion.

You can see why this gives the base b expansion of a number x by writing

$$x = \dfrac{a_0}{b} + \dfrac{a_1}{b^2} + \dfrac{a_2}{b^3} + \cdots.$$

The digits I want are $a_0$ , $a_1$ , and so on. Multiplying x by b gives

$$b x = a_0 + \dfrac{a_1}{b} + \dfrac{a_2}{b^2} + \cdots.$$

The integer part is $a_0$ , and the fractional part is

$$b x - a_0 = \dfrac{a_1}{b} + \dfrac{a_2}{b^2} + \cdots.$$

Then I get $a_1$ by multiplying this by b, and so on.

Thus, $0.3 = (0.\overline{2046})_7$ .

21. Express $(0.54242\ldots)_6 = (0.5 \overline{42})_6$ as a decimal fraction in lowest terms.

Let $x = (0.54242 \ldots)_6$ . Since the repeating part has two digits, I multiply by $6^2$ to get

$$\eqalign{ 36 x & = (54.2\, 4242 \ldots)_6 \cr x & = (\ \, 0.5\, 4242 \ldots)_6 \cr \noalign{\vskip2 pt \hrule \vskip2 pt} 35 x & = (53.\, 3)_6 \cr}$$

Here's an explanation for the subtraction. The repeating 42's on the far right cancel. In the place to the right of the point, I'm doing 2 minus 5. As usual, I have to borrow 1 from the 4 to the left, which is where the "53" comes from. After borrowing, in the place to the right of the point, I'm doing $(12)_6 - 5_6$ . This is $8 - 5 = 3$ in decimal, so the digit to the right of the point is 3.

I still have to convert $(53.3)_6$ to decimal before I solve for x:

$$(53.3)_6 = 5 \cdot 6 + 3 + 3 \cdot \dfrac{1}{6} = \dfrac{67}{2}.$$

So

$$\eqalign{ 35 x & = \dfrac{67}{2} \cr \noalign{\vskip2 pt} x & = \dfrac{67}{70} \quad\halmos \cr}$$

22. Let b be a positive integer greater than 3. Express $(0.3(b - 1)3(b - 1) \ldots)_b = (0.\overline{3(b - 1)})_b$ as a rational function of b.

Write the expression as an infinite series and use the formula for the sum of a geometric series:

$$(0.3(b - 1)3(b - 1) \ldots)_b = \dfrac{3}{b} + \dfrac{b - 1}{b^2} + \dfrac{3}{b^3} + \dfrac{b - 1}{b^4} + \cdots = \dfrac{3 b + (b - 1)}{b^2} + \dfrac{3 b + (b - 1)}{b^4} + \cdots =$$

$$\dfrac{4 b - 1}{b^2} + \dfrac{4 b - 1}{b^4} + \cdots = \dfrac{\dfrac{4 b - 1}{b^2}}{1 - \dfrac{1}{b^2}} = \dfrac{4 b - 1}{b^2 - 1}.\quad\halmos$$

23. Let b be a positive integer greater than 3. Find the base b expansion of $\dfrac{2 b^2 + 1}{b^2 - 1}$ .

The idea in this problem is to try to expand the expression in a power series in $\dfrac{1}{b}$ . One way to do this is to make use of the geometric series

$$\dfrac{1}{1 - x} = 1 + x + x^2 + x^3 + \cdots.$$

If $x = \dfrac{1}{b^k}$ for some k, I'll get a power series in $\dfrac{1}{b}$ . So I do some algebra to get expressions of the right form.

$$\dfrac{2 b^2 + 1}{b^2 - 1} = \dfrac{2 + \dfrac{1}{b^2}}{1 - \dfrac{1}{b^2}} = 2 \cdot \dfrac{1}{1 - \dfrac{1}{b^2}} + \dfrac{1}{b^2}\cdot \dfrac{1}{1 - \dfrac{1}{b^2}} = 2 \cdot \left(1 + \dfrac{1}{b^2} + \dfrac{1}{b^4} + \cdots\right) + \dfrac{1}{b^2}\cdot \left(1 + \dfrac{1}{b^2} + \dfrac{1}{b^4} + \cdots\right) =$$

$$\left(2 + \dfrac{2}{b^2} + \dfrac{2}{b^4} + \cdots\right) + \left(\dfrac{1}{b^2} + \dfrac{1}{b^4} + \dfrac{1}{b^6} +\cdots\right) = 2 + \dfrac{3}{b^2} + \dfrac{3}{b^4} + \dfrac{3}{b^6} + \cdots = (2.\overline{03})_b.\quad\halmos$$

24. Find the finite continued fraction expansion for $\dfrac{983}{237}$ .

Do the Euclidean algorithm:

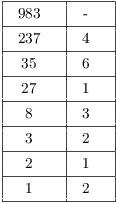
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 983 & & - & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 237 & & 4 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 35 & & 6 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 27 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 8 & & 3 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 3 & & 2 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 2 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1 & & 2 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\dfrac{983}{237} = [4, 6, 1, 3, 2, 1, 2].\quad\halmos$$

25. Find the successive convergents and the exact value of the finite continued fraction $[3, 1, 4, 1, 1, 6]$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & a & & p & & q & & c & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 3 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 4 & & 1 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 4 & & 19 & & 5 & & $\dfrac{19}{5}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 23 & & 6 & & $\dfrac{23}{6}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 42 & & 11 & & $\dfrac{42}{11}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 6 & & 275 & & 72 & & $\dfrac{275}{72}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$[3, 1, 4, 1, 1, 6] = \dfrac{275}{72}.\quad\halmos$$

26. Suppose x is a positive integer. Find the exact value of

$$1 + \dfrac{1}{x + \dfrac{1}{x^2 + \dfrac{1}{x^3}}}.$$

The expression is the finite continued fraction $[1, x, x^2, x^3]$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & a & & p & & q & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & x & & $x + 1$ & & x & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $x^2$ & & $x^3 + x^2 + 1$ & & $x^3 + 1$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $x^3$ & & $x^6 + x^5 + x^3 + x + 1$ & & $x^6 + x^3 + x$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$1 + \dfrac{1}{x + \dfrac{1}{x^2 + \dfrac{1}{x^3}}} = \dfrac{x^6 + x^5 + x^3 + x + 1}{x^6 + x^3 + x}.\quad\halmos$$

27. Use continued fractions to find an integer linear combination of 501 and 113 which is equal to 1.

First, find the continued fraction expansion of $\dfrac{501}{113}$ :

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 501 & & - & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 113 & & 4 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 49 & & 2 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 15 & & 3 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 4 & & 3 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 3 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1 & & 3 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\dfrac{501}{113} = [4, 2, 3, 3, 1, 3].$$

Next, find the convergents:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & a & & p & & q & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 4 & & 4 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 9 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 3 & & 31 & & 7 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 3 & & 102 & & 23 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 133 & & 30 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 3 & & 501 & & 113 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Finally, take the "cross product" of the p's and q's in the last two rows:

$$30 \cdot 501 + (-133) \cdot 113 = 1.\quad\halmos$$

To be honest, one must be inconsistent. - H. G. Wells

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga