The Chinese Remainder Theorem

The Chinese Remainder Theorem says that certain systems of simultaneous congruences with different moduli have solutions. The idea embodied in the theorem was known to the Chinese mathematician Sunzi in the $3^{\rm rd}$ century A.D. --- hence the name.

I'll begin by collecting some useful lemmas.

Lemma 1. Let m and $a_1$ , ..., $a_n$ be positive integers. If m is relatively prime to each of $a_1$ , ..., $a_n$ , then it is relatively prime to their product $a_1\cdots a_n$ .

Proof. If $(m, a_1 \cdots a_n) \ne 1$ , then there is a prime p which divides both m and $a_1 \cdots a_n$ . Now $p \mid a_1 \cdots a_n$ , so p must divide $a_i$ for some i. But p divides both m and $a_i$ , so $(m, a_i) \ne 1$ . This contradiction implies that $(m, a_1 \cdots a_n) = 1$ .

For example, 6 is relatively prime to 25, to 7, and to 11. Now $25 \cdot 7 \cdot 11 = 1925$ , and $(6, 1925) = 1$ .

I showed earlier that the greatest common divisor $(a, b)$ of a and b is greatest in the sense that it is divisible by any common divisor of a and b. The next result is the analogous statement for least common multiples.

Lemma 2. Let m and $a_1$ , ..., $a_n$ be positive integers. If m is a multiple of each of $a_1$ , ..., $a_n$ , then m is a multiple of $[a_1, \ldots, a_n]$ .

Proof. By the Division Algorithm, there are unique numbers q and r such that

$$m = q \cdot [a_1, \ldots, a_n] + r, \hbox{ where } 0 \le r < [a_1, \ldots, a_n].$$

Now $a_i$ divides both m and $[a_1, \ldots, a_n]$ , so $a_i$ divides r. Since this is true for all i, r is a common multiple of the $a_i$ smaller than the least common multiple $[a_1, \ldots, a_n]$ . This is only possible if $r = 0$ . Then $m = q\cdot [a_1, \ldots, a_n]$ , i.e. m is a multiple of $[a_1, \ldots, a_n]$ .

For instance, 88 is a multiple of 4 and 22. The least common multiple of 4 and 22 is 44, and 88 is also a multiple of 44.

Lemma 3. Let $a_1$ , ..., $a_n$ be positive integers. If $a_1$ , ..., $a_n$ are pairwise relatively prime (that is, $(a_i, a_j) = 1$ for $i \ne j$ ), then

$$[a_1, \ldots, a_n] = a_1\cdots a_n.$$

Proof. Induct on n. The statement is trivially true for $n = 1$ , so I'll start with $n = 2$ . The statement for $n = 2$ follows from the equation $xy = [x, y](x, y)$ :

$$[a_1, a_2] = \dfrac{a_1 a_2}{(a_1, a_2)} = \dfrac{a_1 a_2}{1} = a_1 a_2.$$

Now assume $n > 2$ , and assume the result is true for n. I will prove that it holds for $n + 1$ .

Claim: $\left[[a_1, \ldots, a_n], a_{n+1}\right] = [a_1, \ldots, a_n, a_{n+1}]$ .

(Some people take this as an iterative definition of $[a_1, \ldots, a_n, a_{n+1}]$ .) $[a_1, \ldots, a_n, a_{n+1}]$ is a multiple of each of $a_1$ , ..., $a_n$ , so by Lemma 2 it's a multiple of $[a_1, \ldots, a_n]$ . It's also a multiple of $a_{n+1}$ , so

$$\left[[a_1, \ldots, a_n], a_{n+1}\right] \bigm| [a_1, \ldots, a_n, a_{n+1}].$$

On the other hand, for $i = 1, \ldots, n$ ,

$$a_i \bigm| [a_1, \ldots, a_n] \quad\hbox{and}\quad [a_1, \ldots, a_n] \bigm| \left[[a_1, \ldots, a_n], a_{n+1}\right].$$

Therefore,

$$a_i \bigm| \left[[a_1, \ldots, a_n], a_{n+1}\right].$$

Obviously,

$$a_{n+1} \bigm| \left[[a_1, \ldots, a_n], a_{n+1}\right].$$

Thus, $\left[[a_1, \ldots, a_n], a_{n+1}\right]$ is a common multiple of all the $a_i$ 's. Since $[a_1, \ldots, a_n, a_{n+1}]$ is the least common multiple, Lemma 2 implies that

$$[a_1, \ldots, a_n, a_{n+1}] \bigm| \left[[a_1, \ldots, a_n], a_{n+1}\right].$$

Since I have two positive numbers which divide one another, they're equal:

$$\left[[a_1, \ldots, a_n], a_{n+1}\right] = [a_1, \ldots, a_n, a_{n+1}].$$

This proves the claim.

Returning to the proof of the induction step, I have

$$[a_1, \ldots, a_n, a_{n+1}] = \left[[a_1, \ldots, a_n], a_{n+1}\right] = [a_1\cdots a_n, a_{n+1}] = a_1\cdots a_n a_{n+1}.$$

The second equality follows by the induction hypothesis (the statement for n). The third equality follows from Lemma 1 and the result for $n = 2$ .

As an example, 6, 25, and 7 are relatively prime (in pairs). The least common multiple is $[6, 25, 7] = 1050 = 6 \cdot 25 \cdot 7$ .

Theorem. ( The Chinese Remainder Theorem) Suppose $m_1$ , ..., $m_n$ are pairwise relatively prime (that is, $(m_i, m_j) = 1$ for $i \ne j$ ). Then the following system of congruences has a unique solution mod $m_1 m_2 \cdots m_n$ :

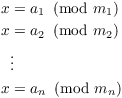
$$\eqalign{ x & = a_1 \mod{m_1} \cr x & = a_2 \mod{m_2} \cr & \vdots \cr x & = a_n \mod{m_n} \cr}$$

Notation.

$$x_1 x_2 \cdots \widehat{x_i} \cdots x_n \quad\hbox{means}\quad x_1 x_2 \cdots x_i \cdots x_n \quad\hbox{omitting}\quad x_i.$$

For example,

$$x_1 x_2 \cdots \widehat{x_4} \cdots x_6 \quad\hbox{means}\quad x_1 x_2 x_3 x_5 x_6.$$

This is a convenient (and standard) notation for omitting a single variable term in a product of things.

Proof. Define

$$p_k = m_1\cdots \widehat{m_k} \cdots m_n.$$

That is, $p_k$ is the product of the m's with $m_k$ omitted. By Lemma 1, $(p_k, m_k) = 1$ . Hence, there are numbers $s_k$ , $t_k$ such that

$$s_k p_k + t_k m_k = 1.$$

In terms of congruences,

$$s_k p_k = 1 \mod{m_k}.$$

Now let

$$x = a_1 p_1 s_1 + a_2 s_2 p_2 + \cdots + a_n p_n s_n.$$

If $j \ne k$ , then $m_k \mid p_j$ , so mod $m_k$ all the terms but the k-th term are 0 mod $m_k$ :

$$x = a_k p_k s_k = a_k \cdot 1 = a_k \mod{m_k}.$$

This proves that x is a solution to the system of congruences (and incidentally, gives a formula for x).

Now suppose that x and y are two solutions to the system of congruences.

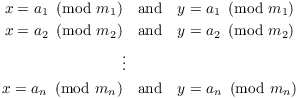
$$\eqalign{ x = a_1 \mod{m_1} & \quad\hbox{and}\quad y = a_1 \mod{m_1} \cr x = a_2 \mod{m_2} & \quad\hbox{and}\quad y = a_2 \mod{m_2} \cr & \vdots \cr x = a_n \mod{m_n} & \quad\hbox{and}\quad y = a_n \mod{m_n} \cr}$$

Then

$$x = a_k = y \mod{m_k} \quad\hbox{so}\quad x - y = 0 \mod{m_k} \quad\hbox{or}\quad m_k \mid x - y.$$

Thus, $x - y$ is a multiple of all the m's, so

$$[m_1, \ldots, m_n] \mid x - y.$$

But the m's are pairwise relatively prime, so by Lemma 3,

$$m_1 \cdots m_n \mid x - y, \quad\hbox{or}\quad x = y \mod{m_1 \cdots m_n}.$$

That is, the solution to the congruences is unique mod $m_1 \cdots m_n$ .

Example. Solve

$$\eqalign{ x & = 2 \mod{4} \cr x & = 7 \mod{9} \cr}.$$

$(4, 9) = 1$ , so there is a unique solution mod 36. Following the construction of x in the proof,

$$p_1 = 9, \quad 9 \cdot 1 = 1 \mod{4}, \quad\hbox{so}\quad s_1 = 1$$

$$p_2 = 4, \quad 4 \cdot 7 = 1 \mod{9}, \quad\hbox{so}\quad s_2 = 7$$

Solution:

$$x = a_1 p_1 s_1 + a_2 p_2 s_2 = 18 + 196 = 214 = 34 \mod{36}.\quad\halmos$$

Example. Solve

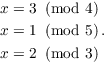
$$\eqalign{ x & = 3 \mod{4} \cr x & = 1 \mod{5} \cr x & = 2 \mod{3} \cr}.$$

The moduli are pairwise relatively prime, so there is a unique solution mod 60. This time, I'll solve the system using an iterative method.

$$x = 3 \mod{4}, \quad\hbox{so}\quad x = 3 + 4 s.$$

But $x = 1 \mod{5}$ , so

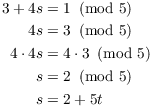
$$\eqalign{ 3 + 4 s & = 1 \mod{5} \cr 4 s & = 3 \mod{5} \cr 4 \cdot 4 s & = 4 \cdot 3 \mod{5} \cr s & = 2 \mod{5} \cr s & = 2 + 5 t \cr}$$

Hence,

$$x = 3 + 4 s = 3 + 4(2 + 5 t) = 11 + 20 t.$$

Finally, $x = 2 \mod{3}$ , so

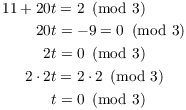
$$\eqalign{ 11 + 20 t & = 2 \mod{3} \cr 20 t & = -9 = 0 \mod{3} \cr 2 t & = 0 \mod{3} \cr 2 \cdot 2 t & = 2 \cdot 2 \mod{3} \cr t & = 0 \mod{3} \cr}$$

Hence, $t = 3 u$ .

Now put everything back:

$$x = 11 + 20 t = 11 + 20(3 u) = 11 + 60 u, \quad\hbox{or}\quad x = 11 \mod{60}.\quad\halmos$$

Example. Calvin Butterball keeps pet meerkats in his backyard. If he divides them into 5 equal groups, 4 are left over. If he divides them into 8 equal groups, 6 are left over. If he divides them into 9 equal groups, 8 are left over. What is the smallest number of meerkats that Calvin could have?

Let x be the number of meerkats. Then

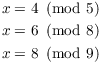
$$\eqalign{ x & = 4 \mod{5} \cr x & = 6 \mod{8} \cr x & = 8 \mod{9} \cr}$$

From $x = 4 \mod{5}$ , I get $x = 4 + 5 a$ . Plugging this into the second congruence, I get

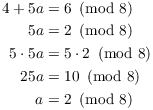
$$\eqalign{ 4 + 5 a & = 6 \mod{8} \cr 5 a & = 2 \mod{8} \cr 5 \cdot 5 a & = 5 \cdot 2 \mod{8} \cr 25 a & = 10 \mod{8} \cr a & = 2 \mod{8} \cr}$$

Hence, $a = 2 + 8 b$ . Plugging this into $x = 4 + 5 a$ gives

$$x = 4 + 5(2 + 8 b) = 14 + 40 b.$$

Plugging this into the third congruence, I get

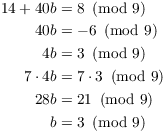
$$\eqalign{ 14 + 40 b & = 8 \mod{9} \cr 40 b & = -6 \mod{9} \cr 4 b & = 3 \mod{9} \cr 7 \cdot 4 b & = 7 \cdot 3 \mod{9} \cr 28 b & = 21 \mod{9} \cr b & = 3 \mod{9} \cr}$$

Hence, $b = 3 + 9 c$ . Plugging this into $x = 14 + 40 b$ gives

$$x = 14 + 40(3 + 9 c) = 134 + 360 c.$$

The smallest positive value of x is obtained by setting $c = 0$ , which gives $x = 134$ .

You can sometimes solve a system even if the moduli aren't relatively prime; the criteria are similar to those for solving system of linear Diophantine equations.\blank

Theorem. Consider the system

$$\eqalign{ x & = a_1 \mod{m_1} \cr x & = a_2 \mod{m_2} \cr}.$$

(a) If $(m_1, m_2) \notdiv a_1 - a_2$ , there are no solutions.

(b) If $(m_1, m_2) \mid a_1 - a_2$ , there is a unique solution mod $[m_1, m_2]$ .

Note that if $(m_1, m_2) = 1$ , case (b) automatically holds, and $[m_1, m_2] = m_1 m_2$ --- i.e. I get the Chinese Remainder Theorem for $n = 2$ .

Proof. (a) I'll prove the contrapositive. Suppose x is a solution to the system of congruences, so

$$x = a_1 \mod{m_1} \quad\hbox{and}\quad x = a_2 \mod{m_2}.$$

The first congruence gives $x - a_1 = 0 \mod{m_1}$ , so $m_1 \mid x - a_1$ . Similarly, $m_2 \mid x - a_2$ . But $(m_1, m_2) \mid m_1$ and $(m_1, m_2) \mid m_2$ , so

$$(m_1, m_2) \mid x - a_1 \quad\hbox{and}\quad (m_1, m_2) \mid x - a_2.$$

Therefore,

$$(m_1, m_2) \mid (x - a_2) - (x - a_1) = a_1 - a_2.$$

This proves the contrapositive of the assertion, so (a) is true.

(b) First, suppose that if x and y are solutions to the system.

$$x = a_1 \mod{m_1} \quad\hbox{and}\quad y = a_1 \mod{m_1} \quad\hbox{give}\quad x - y = 0 \mod{m_1}.$$

Thus, $m_1 \mid x - y$ . Similarly, $m_2 \mid x - y$ . Since $x - y$ is a multiple of $m_1$ and $m_2$ , it is a multiple of $[m_1, m_2]$ . Thus,

$$x - y = 0 \mod{[m_1, m_2]}, \quad\hbox{so}\quad x = y \mod{[m_1, m_2]}.$$

Thus, any two solutions are congruent mod $[m_1, m_2]$ .

Now suppose $(m_1, m_2) \mid a_1 - a_2$ , so $a_1 - a_2 = k (m_1. m_2)$ for some $k \in \integer$ . Note that

$$\left(\dfrac{m_1}{(m_1, m_2)}, \dfrac{m_2}{(m_1, m_2)}\right) = 1.$$

It follows that $\dfrac{m_1}{(m_1, m_2)}$ is invertible mod $\dfrac{m_2}{(m_1, m_2)}$ , so there is an integer p such that

$$p \dfrac{m_1}{(m_1, m_2)} = 1 \mod{\dfrac{m_2}{(m_1, m_2)}}.$$

I claim that the following is a solution to the system for all $t \in \integer$ :

$$x = a_1 - p k m_1 + t [m_1, m_2].$$

You can obtain this "guess" by working backwards from the system assuming there is a solution, and solving the congruences by basic algebra. I will omit the details.

First, since $m_1 \mid [m_1, m_2]$ ,

$$x = a_1 - p k m_1 + t [m_1, m_2] = a_1 \mod{m_1}.$$

This shows that the proposed solution satisfies the first congruence.

Next. I need to reduce $x = a_1 - p k m_1 + t [m_1, m_2]$ mod $m_2$ and show that I get $a_2$ . I'll need the following facts. First, since $a_1 - a_2 = k (m_1. m_2)$ , we have $a_1 = a_2 + k (m_1, m_2)$ .

Second, since $p \dfrac{m_1}{(m_1, m_2)} = 1 \mod{\dfrac{m_2}{(m_1, m_2)}}$ , we have

$$1 - p \dfrac{m_1}{(m_1, m_2)} = j \dfrac{m_2}{(m_1, m_2)} \quad\hbox{for some}\quad j \in \integer.$$

Hence,

$$x = a_1 - p k m_1 + t [m_1, m_2] = a_2 + k (m_1, m_2) - p k m_1 + t [m_1, m_2] =$$

$$a_2 + k (m_1, m_2) - p k m_1 + t [m_1, m_2] = a_2 + k (m_1, m_2) \left(1 - p \dfrac{m_1}{(m_1, m_2)}\right) + t [m_1, m_2] =$$

$$a_2 + k (m_1, m_2) \cdot j \dfrac{m_2}{(m_1, m_2)} + t [m_1, m_2] = a_2 + k j m_2 + t [m_1, m_2] = a_2 \mod{m_2}.$$

This shows that $x = a_1 - p k m_1 + t [m_1, m_2]$ solves the congruences for all $t \in \integer$ --- and so $x = a_1 - p k m_1$ is a solution mod $[m_1, m_2]$ . Our initial observation shows that this is the only solution mod $[m_1, m_2]$ .

Let's look at an example to show how this works. Suppose we have the system of congruences

$$\eqalign{ x & = 21 \mod{24} \cr x & = 1 \mod{28} \cr}$$

We have $a_1 = 21$ , $a_2 = 1$ , $m_1 = 24$ , and $m_2 = 28$ . Since $(24, 28) = 4 \mid 21 - 1$ , the condition for a solution is satisfied.

First, $k = \dfrac{a_1 - a_2}{(m_1, m_2)} = \dfrac{20}{4} = 5$ .

Next,

$$\dfrac{m_1}{(m_1, m_2)} = \dfrac{24}{4} = 6 \quad\hbox{and}\quad \dfrac{m_2}{(m_1, m_2)} = \dfrac{28}{4} = 7.$$

The multiplicative inverse of 6 mod 7 is $p = 6$ . (You can find this by trial and error, or using the Extended Euclidean Algorithm.) A solution mod $[m_1, m_2] = [24, 28] = 168$ is

$$x = a_1 - p k m_1 = 21 - 6 \cdot 5 \cdot 24 = -899 = 141 \mod{168}.$$

You can check that 141 solves the original congruences.

Example. Solve

$$\eqalign{ x & = 5 \mod{12} \cr x & = 11 \mod{18} \cr}.$$

Since $(12, 18) = 6 \mid 11 - 5$ , there is a unique solution mod $[12, 18] = 36$ . I'll use the iterative method to find the solution.

$$x = 5 \mod{12}, \quad\hbox{so}\quad x = 5 + 12 s.$$

Since $x = 11 \mod{18}$ ,

$$\eqalign{ 5 + 12 s & = 11 \mod{18} \cr 12 s & = 6 \mod{18} \cr}$$

Now I use my rule for "dividing" congruences: 6 divides both 12 and 6, and $(6, 18) = 6$ , so I can divide through by 6:

$$2 s = 1 \mod{3}.$$

Multiply by 2, and convert the congruence to an equation:

$$s = 2 \mod{3}, \quad s = 2 + 3 t.$$

Plug back in:

$$\eqalign{ x & = 5 + 12 s = 5 + 12(2 + 3 t) = 29 + 36 t \cr x & = 29 \mod{36} \cr} \quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2022 by Bruce Ikenaga