Groups

Definition. A binary operation on a set S is a function which takes a pair of elements $s, t \in S$ and produces another element $f(s, t) \in S$ . That is, a binary operation is a function $f: S \times S \to S$ .

Binary operations are usually denoted by infix operators:

$s \cdot t \quad\hbox{or}\quad s \ast t \quad\hbox{or even}\quad s t \quad\hbox{rather than}\quad f(s, t).$

(The last notation --- suppressing the operation symbol entirely --- is what you do when you write " " to mean "3 times x". In this case, the operation is multiplication.)

When you are trying to show that you have a binary operation $\ast$ on a set S, the issue is usually whether S is closed under the operation. This means that for all $s, t \in S$ , you have $s \ast t \in S$ .

As with any universal statement ("for all $s, t \in S$ "), to prove that $\ast$ is a binary operation on S you must show that it holds for arbitrary s and t. You are not allowed to pick specific elements s and t in the set.

On the other hand, if you think that S is not closed under $\ast$ , you need to give a specific counterexample. You can disprove a universal statement with a single counterexample.

Most binary operations satisfy additional properties. Here are two that are particularly important.

Definition. Let $\ast$ be a binary operation on a set S.

(a) $\ast$ is associative if $a \ast (b \ast c) = (a \ast b) \ast c$ for all $a, b, c \in S$ .

(b) $\ast$ is commutative if $a \ast b = b \ast a$ for all $a, b \in S$ .

Note that associativity is stated for 3 elements. You can prove (using induction) that if associativity holds for 3 elements, then it holds for n elements for any $n \ge 3$ .

Example. If $\ast$ is an associative binary operation, show that

$a \ast [(b \ast c) \ast d] = [(a \ast b) \ast c)] \ast d.$

Use 3-element associativity step-by-step:

$\eqalign{ a \ast [(b \ast c) \ast d] & = a \ast [b \ast (c \ast d)] \cr & = (a \ast b) \ast (c \ast d) \cr & = [(a \ast b) \ast c] \ast d \cr}$

Of course, this is just a particular case, but it should make it plausible that you could do this with any two groupings of n elements.

Example. ( Binary operations on familiar number systems) Are addition, subtraction, multiplication, and division binary operations on the integers $\integer$ , the rational numbers $\rational$ , the real numbers $\real$ , and the complex numbers $\complex$ ?

For those which are binary operations, are they associative? Commutative?

Addition, subtraction, and multiplication are binary operations on the integers $\integer$ , the rational numbers $\rational$ , the real numbers $\real$ , and the complex numbers $\complex$ .

For example, consider the operation of addition on the set of integers. If you add two integers, you get a well-defined integer as the result. Addition is therefore a binary operation on $\integer$ .

Addition and multiplication are both associative and commutative operations on $\integer$ , $\rational$ , $\real$ , and $\complex$ .

Subtraction is not associative:

$(3 - 4) - 6 = -1 - 6 = -7, \quad\hbox{but}\quad 3 - (4 - 6) = 3 - (-2) = 5.$

Subtraction is also not commutative:

$8 - 9 = -1, \quad\hbox{but}\quad 9 - 8 = 1.$

Since the counterexamples I gave used only integers, which are elements of $\integer$ , $\rational$ , $\real$ , and $\complex$ , the last two statements are true for all of these sets.

Division is not a binary operation on any of these sets. For one thing, you cannot divide by 0. For example, $0 \in \integer$ and $3 \in \integer$ but $\dfrac{3}{0} \notin \integer$ .

Example. ( A binary operation defined by a table) Consider the following operation table:

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $\ast$ & & a & & b & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & a & & b & & a & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & b & & a & & a & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

Find $a \ast a$ , $a \ast b$ , $b \ast a$ , and $b \ast b$ .

Is the operation commutative? Is the operation associative?

The first row says that

$a \ast a = b \quad\hbox{and}\quad a \ast b = a.$

The second row says that

$b \ast a = a \quad\hbox{and}\quad b \ast b = a.$

(The first element is the row element and the second element is the column element.)

$\ast$ is commutative --- in fact, this follows from the fact that the table is symmetric about the main diagonal (the diagonal running from northwest to southeast).

However, $\ast$ is not associative:

$b \ast (a \ast a) = b \ast b = a, \quad\hbox{but}\quad (b \ast a) \ast a = a \ast a = b.$

It's possible to define a binary operation using a table if the set is small. If the set is too large or the set is infinite, this isn't useful or possible.

Example. ( Function composition as a binary operation) If X is a set and $\hom(X,X)$ is the set of functions from X to X, then function composition is a binary operation on $\hom(X,X)$ .

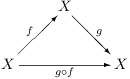
$\sarrowlength=0.42\harrowlength \commdiag{ & X & \cr & \arrow(1,1)\lft{f} \quad \arrow(1,-1)\rt{g} & \cr X & \mapright_{g\circ f} & X \cr}$

As the diagram shows, if $f: X \to X$ and $g: X \to X$ are functions, then the composite $g \circ f: X \to X$ is another function from X to X.

Example. ( An "operation" which isn't well-defined) If $a, b \in \integer$ , can I define $a \ast b$ to be "an integer bigger than "? That is, does this define a binary operation on $\integer$ ?

In this case, the supposed operation apparently produces an integer, so the issue is not whether the set is closed under the operation. The problem is that "an integer bigger than " does not define a unique integer. For example, if and , then $a b = 3 \cdot 2 = 6$ . The definition would allow $a \ast b$ to be 7 (since , but $a \ast b = 15$ would also work (since ).

The input does not produce a unique output $a \ast b$ : that is, $\ast$ does not define a function from pairs of integers to integers. Thus, $\ast$ is not a binary operation.

Definition. A group is a set G with a binary operation $\ast$ such that:

(a) ( Associativity) $a \ast (b \ast c) = (a \ast b) \ast c$ for all $a, b, c \in G$ .

(b) ( Identity) There is an element $e \in G$ such that $e \ast a = a = a \ast e$ for all $a \in G$ .

(c) ( Inverses) For each $a \in G$ , there is an element $a' \in G$ (the inverse of a) such that $a \ast a' = e = a' \ast a$ .

The notations " $\ast$ " for the operation, "e" for the identity, and " " for the inverse of a are temporary, for the sake of making the definition. In particular examples, you'll see that other notations are used. And I'll say something about the general issue of notation in groups later on.

Notice that the operation in a group does not need to be commutative. That is, $a \ast b$ need not equal $b \ast a$ .

Definition. A group is abelian if the group operation is commutative --- that is, $a \ast b = b \ast a$ for all a and b.

The term "abelian" honors Niels Henrik Abel (1802--1829). Abel and Paolo Ruffini were the first to demonstrate the unsolvability of the general quintic equation.

Most of the initial examples will be of abelian groups. I'll give an example of a non-abelian group later.

Definition. The order of a group is the number of elements in the group, if it is finite. Otherwise, the group has infinite order. denotes the order of the group G.

A finite group is a group whose order is finite; an infinite group is a group whose order is infinite.

Example. ( Group structures on familiar number systems) Consider the following sets:

$\integer$ - the set of integers

$\rational$ - the set of rational numbers

$\real$ - the set of real numbers

$\complex$ - the set of complex numbers

Are these groups with addition as the operation?

All of them are infinite groups under addition.

Consider, for example, the case of $(\integer, +)$ . The sum of two integers is an integer. Addition of integers is associative. 0 is an identity for addition. And if $x \in \integer$ , the additive inverse of x is , another integer.

Example. ( The nonnegative rationals under addition) Consider the set of nonzero rational numbers:

$\rational^+ = \{q \in \rational \mid q > 0\}.$

Is $\rational^+$ a group under addition? Under multiplication?

$\rational^+$ is not a group under addition.

$\rational^+$ is certainly closed under addition, and addition of rational numbers is associative. However, it does not contain an identity for addition.

Suppose $e \in \rational^+$ was the identity. Then, for instance,

$e + 17 = 17, \quad\hbox{so}\quad e = 0.$

But $0 \notin \rational^+$ .

(Note that in giving this proof by contradiction, I can't begin by assuming that 0 is the identity: I had to show it would have to be, by the definition.)

(Question: Suppose you try to fix this problem by considering the nonnegative rational numbers $\rational^{\ge 0}$ under addition. Now 0 is an identity for addition in $\rational^{\ge 0}$ . But something else goes wrong and $\rational^{\ge 0}$ is not a group. Do you see what it is?)

$\rational^+$ is a group under multiplication. The product of two rational numbers is rational number:

$\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{a c}{b d}, \quad a, b, c, d \in \integer.$

Since, in addition, the product of two positive numbers is positive, $\rational^+$ is closed under multiplication.

Multiplication of rationals is associative. The identity for multiplication is 1, which is a positive rational number. Finally, if $\dfrac{a}{b}$ is a positive rational number, then so is its multiplicative inverse $\dfrac{b}{a}$ .

Notation. It's tedious to have to write " $\ast$ " for the operation in a group. It's common to use either multiplicative or additive notation instead. Here is how the various notations compare.

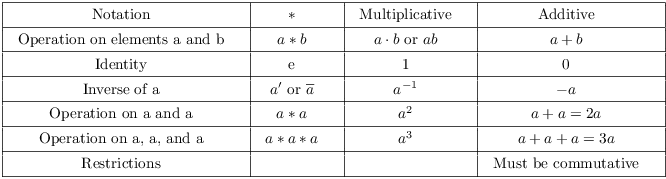
$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & Notation & & $\ast$ & & Multiplicative & & Additive & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & Operation on elements a and b & & $a \ast b$ & & $a \cdot b$ or $ab$ & & $a + b$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & Identity & & e & & 1 & & 0 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & Inverse of a & & $a'$ or $\overline{a}$ & & $a^{-1}$ & & $-a$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & Operation on a and a & & $a \ast a$ & & $a^2$ & & $a + a = 2 a$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & Operation on a, a, and a & & $a \ast a \ast a$ & & $a^3$ & & $a + a + a = 3 a$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & Restrictions & & & & & & Must be commutative & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

Note that the convention is to use multiplicative notation for an arbitrary group (unless you know it's abelian, in which case you may use additive notation).

In multiplicative notation, "1" refers to the identity, which may or may not be the number 1. Likewise, in additive notation, "0" refers to the identity, which may or may not be the number 0.

Of course, if there is a standard way to refer to the operation or the identity element in a group, you use it instead of the general notation. For instance, in the group of integers under addition, you use "+" for the operation --- it would be silly and confusing to use " $\cdot$ "!

And in the group $M(2, \real)$ of $2 \times 2$ matrices with real entries under matrix addition, the identity is

$\left[\matrix{0 & 0 \cr 0 & 0 \cr}\right].$

Example. (a) Write the expression " $a \ast a \ast a \ast b'\,$ " in multiplicative notation and in additive notation. (Assume the operation is commutative, and " " means the inverse of b.)

(b) Write " " in multiplicative notation. (Assume the operation is commutative.)

(a) In multiplicative notation, this is $a^3 b^{-1}$ . In additive notation, this is .

(b) In multiplicative notation, this is $a^5 b^{-1} c^4$ .

I've been referring to the identity of a group and the inverse of an element, but the axioms don't say that there is only one identity, or that an element has only one inverse. The next proposition asserts that the identity and inverses are unique.

Proposition. Let G be a group.

(a) The identity element of G is unique.

(b) The inverse of an element is unique.

Proof. To show a thing is unique, you assume that you have two things of that kind, then show that the two things must in fact be the same.

Suppose 1, are identity elements for G. Then $1\cdot 1' = 1'$ because 1 is an identity, but $1\cdot 1' = 1$ because is an identity. Therefore, $1 = 1\cdot 1' = 1'$ . The identity element of G is unique.

Suppose $g \in G$ and that I have elements $a, b \in G$ which behave like the inverse of g. This means that

$ag = 1 = ga \quad\quad\hbox{and}\quad\quad bg = 1 = gb.$

Now

$ag = 1 \quad\quad\hbox{so}\quad\quad (ag)b = 1\cdot b = b.$

By associativity, , but . So $a \cdot 1 = b$ , and . The inverse of an element is unique.

Associativity applies to 3 elements:

$a \cdot (b \cdot c) = (a \cdot b) \cdot c).$

It's easy to show in particular cases that it applies to products with any number of factors.

Example. Suppose S is a set with an associative binary operation $\cdot$ . Suppose $a, b, c, d \in S$ . Prove that

$(a \cdot b) \cdot (c \cdot d) = a \cdot [(b \cdot c) \cdot d].$

$\eqalign{ (a \cdot b) \cdot (c \cdot d) & = a \cdot [b \cdot (c \cdot d)] \cr & = a \cdot [(b \cdot c) \cdot d] \quad\halmos \cr}$

Proposition. Suppose S is a set with an associative binary operation. Then for all $n \ge 1$ , any two ways of grouping a product of n factors give the same result.

I won't give the proof here, but it isn't too difficult: Use induction. Given this result, from now on, I'll be a little casual about associativity of products with any number of factors.

Proposition. Let G be a group and let $a, b, c \in G$ .

(a) If , then . If , then .

(b) $(a b)^{-1} = b^{-1} a^{-1}$ .

Proof. For the first part of (a), I have

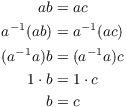
$\eqalign{ a b & = a c \cr a^{-1} (a b) & = a^{-1} (a c) \cr (a^{-1} a) b & = (a^{-1} a) c \cr 1 \cdot b & = 1 \cdot c \cr b & = c \cr}$

You can prove the second part of (a) in similar fashion.

For the proof of (b), I'm going to be a little casual about associativity. I have

$b^{-1} a^{-1} \cdot a b = b^{-1} \cdot 1 \cdot b = b^{-1} \cdot b = 1.$

Lkewise, $a b \cdot b^{-1} a^{-1} = 1$ . So $b^{-1} a^{-1}$ must be the inverse of , i.e. $(a b)^{-1}$ . (The rule $(a b)^{-1} = b^{-1} a^{-1}$ may be familiar to you if you know about matrices, since this is the way you take the inverse of a product of matrices.)

For (c), note that

$a^{-1} \cdot a = 1 = a \cdot a^{-1}.$

This shows that a is the inverse of $a^{-1}$ --- that is, $a = (a^{-1})^{-1}$ .

Notation. If a is an element of a group G with identity 1, then . If n is a positive integer,

$a^n \quad\hbox{means}\quad \overbrace{a \cdot \cdots \cdot a}^{n\ \rm times}.$

If n is a negative integer, means $(a^{-n})^{-1}$ . For example, $a^{-3}$ is defined to be $(a^3)^{-1}$ , the inverse of .

I'm assuming in giving this definition that any two ways of associating a product with n factors gives the same result.

Proposition. Let G be a group and let $a \in G$ .

(a) If , then $a^{-n} = \overbrace{a^{-1} \cdot \cdots \cdot a^{-1}}^{n\ \rm times}$ .

(b) $a^m a^n = a^{m + n}$ for all $m, n \in \integer$ .

I'll omit the proof: It involves induction and is not that enlightening.

Example. ( Computations with group elements) Suppose G is a group and $a, b \in G$ .

(a) Simplify $a^2 b^3 (a b^2)^{-2} a b^3$ as much as possible.

(b) Solve for x in terms of a and b:

(a) Note that I was not told that G was abelian, so I have to be careful not to commute elements (in general).

$\eqalign{ a^2 b^3 (a b^2)^{-2} a b^3 & = a^2 b^3 [(a b^2)^{-1}]^2 a b^3 \cr & = a^2 b^3 [b^{-2} a^{-1}]^2 a b^3 \cr & = a^2 b^3 (b^{-2} a^{-1} b^{-2} a^{-1}) a b^3 \cr & = a^2 b a^{-1} b \cr}\quad\halmos$

(b) I can multiply both sides of the equation by the same thing, but I have to be careful to multiply on the same side of both sides. For example, in the second line below, I multiplied both sides on the left by $a^{-2}$ .

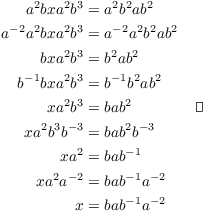
$\eqalign{a^2 b x a^2 b^3 & = a^2 b^2 a b^2 \cr a^{-2} a^2 b x a^2 b^3 & = a^{-2} a^2 b^2 a b^2 \cr b x a^2 b^3 & = b^2 a b^2 \cr b^{-1} b x a^2 b^3 & = b^{-1} b^2 a b^2 \cr x a^2 b^3 & = b a b^2 \cr x a^2 b^3 b^{-3} & = ba b^2 b^{-3} \cr x a^2 & = b a b^{-1} \cr x a^2 a^{-2} & = b a b^{-1} a^{-2} \cr x & = b a b^{-1} a^{-2} \cr}\quad\halmos$

Definition. If G is a group and $g \in G$ , the order of g is the smallest positive integer n such that . If $g^n \ne 1$ for any postive integer n, then g has infinite order.

In this definition, "1" denotes the identity element of G, and I'm using multiplicative notation. Using additive notation, the definition would read: If G is a group and $g \in G$ , the order of g is the smallest positive integer n such that . If $ng \ne 0$ for any postive integer n, then g has infinite order.

Recall that the order of a group is the number of elements in the group; the preceding definition pertains to the order of an element, which is the smallest positive power of the element which equals the identity. Don't confuse the two uses of the word "order"!

Example. ( Orders of elements) This is a group of order 6:

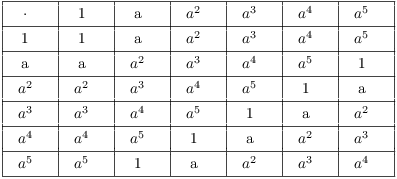
$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot$ & & 1 & & a & & $a^2$ & & $a^3$ & & $a^4$ & & $a^5$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & a & & $a^2$ & & $a^3$ & & $a^4$ & & $a^5$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & a & & a & & $a^2$ & & $a^3$ & & $a^4$ & & $a^5$ & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $a^2$ & & $a^2$ & & $a^3$ & & $a^4$ & & $a^5$ & & 1 & & a & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $a^3$ & & $a^3$ & & $a^4$ & & $a^5$ & & 1 & & a & & $a^2$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $a^4$ & & $a^4$ & & $a^5$ & & 1 & & a & & $a^2$ & & $a^3$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $a^5$ & & $a^5$ & & 1 & & a & & $a^2$ & & $a^3$ & & $a^4$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

Find the orders of the elements of this group.

The operation is multiplication and the identity is 1. To find the order of an element, I find the first positive power which equals 1.

1 has order 1 --- and in fact, in any group, the identity is the only element of order 1.

The element a has order 6 since , and no smaller positive power of a equals 1.

has order 3, because

$a^2 \ne 1, \quad (a^2)^2 = a^4 \ne 1, \quad\hbox{but}\quad (a^2)^3 = a^6 = 1.$

has order 2, because

$a^3 \ne 1, \quad\hbox{but}\quad (a^3)^2 = a^6 = 1.$

has order 3, because

$a^4 \ne 1, \quad (a^4)^2 = a^8 = a^2 \ne 1, \quad\hbox{but}\quad (a^4)^3 = a^{12} = (a^6)^2 = 1.$

has order 6. Note that

$(a^5)^6 = a^{30} = (a^6)^5 = 1.$

You can check that no smaller positive power of gives the identity.

Example. What is the order of $\sqrt{2}$ in $\real$ , the group of real numbers under addition?

The element $\sqrt{2}$ has infinite order: If I take positive multiples of $\sqrt{2}$ , I'll never get 0:

$\sqrt{2}, \quad 2\sqrt{2}, \quad 3\sqrt{2}, \quad \ldots.\quad\halmos$

Example. ( The group of quaternions) This is the group table for Q, the group of quaternions. (Notice that the way i, j, and k multiply is similar to the way the unit vectors $\ihat$ , $\jhat$ , $\khat$ multiply under the cross product in $\real^3$ .)

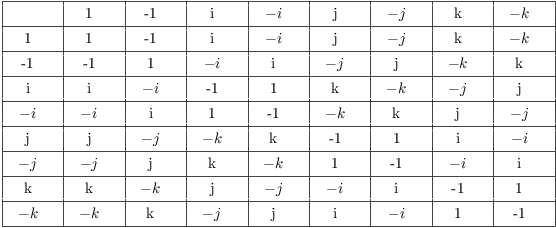
$\vbox{\offinterlineskip \halign{ & \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & 1 & & -1 & & i & & $-i$ & & j & & $-j$ & & k & & $-k$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & -1 & & i & & $-i$ & & j & & $-j$ & & k & & $-k$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & -1 & & -1 & & 1 & & $-i$ & & i & & $-j$ & & j & & $-k$ & & k & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & i & & i & & $-i$ & & -1 & & 1 & & k & & $-k$ & & $-j$ & & j & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $-i$ & & $-i$ & & i & & 1 & & -1 & & $-k$ & & k & & j & & $-j$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & j & & j & & $-j$ & & $-k$ & & k & & -1 & & 1 & & i & & $-i$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $-j$ & & $-j$ & & j & & k & & $-k$ & & 1 & & -1 & & $-i$ & & i & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & k & & k & & $-k$ & & j & & $-j$ & & $-i$ & & i & & -1 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $-k$ & & $-k$ & & k & & $-j$ & & j & & i & & $-i$ & & 1 & & -1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

(a) Show that Q is not abelian.

(b) Find the orders of 1, -1, and i.

(a) Since but (for instance), Q is not abelian.

(b) The identity 1 has order 1, -1 has order 2, and i has order 4:

$i^2 = -1, \quad i^3 = -i, \quad i^4 = (i^2)^2 = (-1)^2 = 1.\quad\halmos$

It's no coincidence that 1, 2, and 4 are divisors of 8, the order of the group. The order of an element always divides the order of the group.

However, it doesn't work the other way: 8 is obviously a divisor of 8, but there's no element of order 8 in Q.

Definition. If G is a group with n elements and G has an element x of order n, G is said to be cyclic of order n.

x is called a generator of the cyclic group, and the cyclic group consists of all powers of x.

Thus, Q is not cyclic, since it has no elements of order 8.

It turns out the $\integer$ is an infinite cyclic group, since you can get every element by taking multiples of 1 (or -1). I'll discuss cyclic groups in more detail later.

Contact information

Bruce Ikenaga's Home Page