Permutation Groups

Recall that the notation $f: X \to Y$ means that f is a function whose domain (set of inputs) is X and whose outputs lie in the set Y. Note that there may be elements of Y which are not outputs of f.

Definition. Let $f: X \to Y$ be a function from a set X to a set Y.

1. f is injective (or one-to-one) if $f(x_1) = f(x_2)$ implies $x_1 = x_2$ for all $x_1, x_2 \in X$ .

2. f is surjective (or onto) if for all $y \in Y$ , there is an $x \in X$ such that $f(x) = y$ .

3. f is bijective (or a one-to-one correspondence) if it is both injective and surjective.

Informally, a function is injective if different inputs always produce different outputs. A function is surjective if everything in the target set is an output of the function.

Example. ( Injective and surjective functions) Show that the function $f: \real \to \real$ given by $f(x) = x^2$ is not injective or surjective.

f is not injective, because

$$f(1) = 1^2 = 1 \quad\hbox{and}\quad f(-1) = (-1)^2 = 1.$$

Nor is f surjective. There is no $x \in \real$ , for instance, such that $f(x) = -1$ .

Note, however, that if $g:\real \to \real^{\ge 0}$ is defined by $g(x) = x^2$ , then g is surjective. ($\real^{\ge 0}$ denotes the set of real numbers greater than or equal to 0.) I just shrunk the target set so that it coincides with the set of outputs of $x^2$ .

Example. ( Injective and surjective functions) Show that the function $f: \real \to \real$ given by $f(x) = e^x$ is injective but not surjective.

f is injective: If two outputs are the same, say

$$f(a) = f(b), \quad\hbox{then}\quad e^a = e^b, \quad\hbox{so}\quad \ln e^a = \ln e^b, \quad\hbox{and}\quad a = b.$$

That is, the inputs must have been the same.

This is one way to show that a function f is injective: Assume that $f(a) = f(b)$ , and prove that $a = b$ .

However, f is not surjective: There is no $x \in \real$ such that $f(x) = -1$ , i.e. such that $e^x = -1$ , because $e^x$ is always positive.

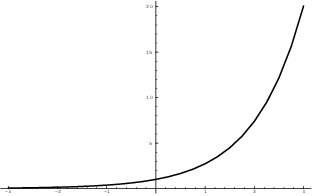
$$\hbox{\epsfysize=1.75 in \epsffile{permutations-1.eps}}$$

You may know that there is a graphical test for injectivity for functions $\real \to \real$ . A function $\real \to \real$ is injective if and only if every horizontal line intersects the graph at most once. You can see that this is true for the graph of $y = e^x$ .

Example. ( Injective and surjective functions) Define $f: \real \to \real$ by

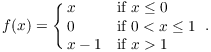
$$f(x) = \cases{x & if $x \le 0$ \cr 0 & if $0 < x \le 1$ \cr x - 1 & if $x > 1$ \cr}.$$

$$\hbox{\epsfysize=1.75 in \epsffile{permutations-2.eps}}$$

Show that f is not injective, but that f is surjective.

f is not injective, since $f(0.5) = 0$ and $f(1) = 0$ : Different inputs can produce the same output.

f is surjective: You can see from the graph that every y-value is an output of the function. To prove this algebraically, I have to show that every $y \in \real$ is an output of f.

If $y \le 0$ , $f(y) = y$ .

If $y > 0$ , then $y + 1 > 1$ , so $f(y + 1) = (y + 1) - 1 = y$ .

To prove a function is surjective, take an arbitrary output y and find an input that produces it. As in this example, your input may be specified in terms of y, since that is given.

While you can show that a function is bijective by showing that it's injective and surjective, there's a method which is usually easier: Simply produce an inverse function.

Definition. Let $f: X \to Y$ be a function from a set X to a set Y. An inverse for f is a function $f^{-1}: Y \to X$ such that:

1. For all $x \in X$ , $f^{-1}\left(f(x)\right) = x$ .

2. For all $y \in Y$ , $f\left(f^{-1}(y)\right) = y$ .

The next result is extremely useful. It asserts that being bijective is the same as having an inverse.

Lemma. Let $f: X \to Y$ be a function from a set X to a set Y. f is bijective if and only if f has an inverse $f^{-1}: Y \to X$ .

Proof. ($\Rightarrow$ ) Suppose that f is bijective. I'll construct the inverse function $f^{-1}: Y \to X$ .

Take $y \in Y$ . Since f is surjective, there is an element $x \in X$ such that $f(x) = y$ . Moreover, x is unique: If $f(x) = y$ and $f(x') = y$ , then $f(x) = f(x')$ . But f is injective, so $x = x'$ .

Define

$$f^{-1}(y) = x.$$

I have defined a function $f^{-1}: Y \to X$ . I must show that it is the inverse of f.

Let $x \in X$ . By definition of $f^{-1}$ , to compute $f^{-1}\left(f(x)\right)$ I must find an element $\hbox{Moe} \in X$ such that $f(\hbox{Moe}) = f(x)$ . But this is easy --- just take $\hbox{Moe} = x$ . Thus, $f^{-1}\left(f(x)\right) = x$ .

Going the other way, let $y \in Y$ . By definition of $f^{-1}$ , to compute $f\left(f^{-1}(y)\right)$ I must find an element $x \in X$ such that $f(x) = y$ . Then $f^{-1}(y) = x$ , so

$$f\left(f^{-1}(y)\right) = f(x) = y.$$

Therefore, $f^{-1}$ really is the inverse of f.

($\Leftarrow$ ) Suppose f has an inverse $f^{-1}: Y \to X$ . I must show f is bijective.

To show that f is surjective, take $y \in Y$ . Then $f\left(f^{-1}(y)\right) = y$ , so I've found an element of X --- namely $f^{-1}(y)$ --- which f maps to y. Therefore, f is surjective.

To show that f is injective, suppose $x_1, x_2 \in X$ and $f(x_1) = f(x_2)$ . Then

$$f^{-1}\left(f(x_1)\right) = f^{-1}\left(f(x_2)\right), \quad\quad\hbox{so}\quad\quad x_1 = x_2.$$

Therefore, f is injective.

Since f is injective and surjective, it's bijective.

This result says that if you want to show a function is bijective, all you have to do is to produce an inverse. In many cases, it's easy to produce an inverse, because an inverse is the function which "undoes" the effect of f.

Example. ( Proving that a function is bijective) Define $f: \real \to \real$ by $f(x) = x^3$ . Show that f is bijective.

The opposite of cubing is taking the cube root, so I'll guess that the inverse is $g(x) = \root 3 \of x$ . Check it:

$$g(f(x)) = g(x^3) = \root 3 \of {x^3} = x, \quad f(g(x)) = f(\root 3 \of x) = (\root 3 \of x)^3 = x.$$

Thus, g is the inverse of f. By the lemma, f is bijective.

Definition. Let A be a set. A permutation of (or on) A is a bijection $A \rightarrow A$ .

Proposition. The set $S_A$ of permutations of a set A is a group under function composition.

Proof. First, the composition of bijections is a bijection: The inverse of $\sigma \cdot \tau$ is $\tau^{-1} \cdot \sigma^{-1}$ . Thus, function composition is a binary operation on the set of bijections from A to A.

Function composition is always associative. The identity map $\id: A \rightarrow A$ is a permutation of A, and serves as an identity under function composition. Since bijective maps have inverses which are bijections, if $\sigma: A \rightarrow A$ is a bijection, so is $\sigma^{-1}$ . Therefore, $S_A$ is a group.

$S_A$ is called the symmetric group on A. If S has n elements, you may as well take $S = \{ 1, 2, \ldots, n\}$ (since it doesn't matter what you call the elements). The corresponding symmetric group is denoted $S_n$ , the symmetric group on n letters.

I'll use $\id$ to denote the identity permutation that sends every element to itself.

One way to write a permutation is to show where each element goes. For example, suppose

$$\sigma = \left(\matrix{ 1 & 2 & 3 & 4 & 5 & 6 \cr 3 & 2 & 4 & 1 & 6 & 5 \cr}\right) \in S_6.$$

I'll refer to this as permutation notation. This means that

$$\sigma(1) = 3, \sigma(2) = 2, \sigma(3) = 4, \sigma(4) = 1, \sigma(5) = 6, \sigma(6) = 5.$$

Thus, the identity permutation in $S_6$ is

$$\id = \left(\matrix{ 1 & 2 & 3 & 4 & 5 & 6 \cr 1 & 2 & 3 & 4 & 5 & 6 \cr}\right).$$

Example. ( Computing a product of permutations) Suppose

$$\sigma = \left(\matrix{ 1 & 2 & 3 & 4 \cr 2 & 3 & 4 & 1 \cr}\right) \quad\hbox{and}\quad \tau = \left(\matrix{ 1 & 2 & 3 & 4 \cr 1 & 3 & 4 & 2 \cr}\right).$$

Compute the product $\tau \sigma$ .

The product $\tau \sigma$ means "$\sigma$ first, then $\tau$ ".

Here's how to compute it:

$$\matrix{ 1 & 2 & 3 & 4 & \cr & & & & \sigma \cr 2 & 3 & 4 & 1 & \cr & & & & \tau \cr 3 & 4 & 2 & 1 & \cr}$$

So

$$\tau \sigma = \left(\matrix{ 1 & 2 & 3 & 4 \cr 3 & 4 & 2 & 1 \cr}\right).$$

Some people prefer to multiply permutations left-to-right: For them, $\tau \sigma$ means "$\tau$ first, then $\sigma$ ". You should probably choose one method and use it all the time, to avoid confusing yourself. The right-to-left approach I used above is consistent with the fact that permutations are functions: In function notation, $(f \circ g)(x)$ means $f(g(x))$ , i.e. "g first, then f".

Example. ( Finding the inverse of a permutation) Find the inverse of the permutation

$$\sigma = \left(\matrix{1 & 2 & 3 & 4 & 5 \cr 3 & 5 & 2 & 4 & 1 \cr}\right).$$

I can find $\sigma^{-1}$ by simply reading $\sigma$ "upside-down".

For example, $\sigma(5) = 1$ , so $\sigma^{-1}(1) = 5$ . In this way, I get

$$\sigma^{-1} = \left(\matrix{ 1 & 2 & 3 & 4 & 5 \cr 5 & 3 & 1 & 4 & 2 \cr}\right).\quad\halmos$$

Permutation notation is fine for computations, but is cumbersome for writing permutations. We can represent permutations more concisely using cycle notation. The idea is like factoring an integer into a product of primes; in this case, the elementary pieces are called cycles.

Definition. A cycle is a permutation which maps a finite subset $\{x_1, x_2, \ldots, x_n\}$ by

$$x_1 \mapsto x_2 \mapsto \cdots \mapsto x_n \mapsto x_1.$$

This cycle will be denoted $(x_1\ x_2\ \ldots\ x_n)$ .

The cycle $(x_1\ x_2\ \ldots\ x_n)$ has length n. For example, the cycle $(7\ 2\ 4)$ has length 3.

Note that a cycle of length n has order n as an element of $S_n$ . For example,

$$(1\ 4\ 2)^3 = \id.$$

A cycle of length 2 is called a transposition. A transposition is a permutation that swaps two elements and leaves everything else fixed. For example, $(3\ 6)$ is the transposition that swaps 3 and 6.

Example. ( Examples of cycles) (a) Write the cycle $(4\ 2 5) \in S_5$ in permutation notation.

(b) Write the permutation $\left(\matrix{1 & 2 & 3 & 4 & 5 \cr 5 & 1 & 4 & 2 & 3 \cr}\right)$ as a cycle.

(a) The cycle $(4\ 2\ 5)$ in $S_5$

$$\left(\matrix{1 & 2 & 3 & 4 & 5 \cr 1 & 5 & 3 & 2 & 4 \cr}\right).$$

(b)

$$\left(\matrix{1 & 2 & 3 & 4 & 5 \cr 5 & 1 & 4 & 2 & 3 \cr}\right) = (1\ 5\ 3\ 4\ 2).\quad\halmos$$

Example. ( The inverse of a cycle) Find the inverse of $(4\ 6\ 2\ 7\ 3)$ .

To find the inverse of a cycle, just run the cycle backwards. Thus,

$$(4\ 6\ 2\ 7\ 3)^{-1} = (3\ 7\ 2\ 6\ 4).\quad\halmos$$

Example. ( Solving a permutation equation) Solve for x:

$$(1\ 4\ 2)^2\cdot x = (2\ 3\ 4)^{-1}.$$

$(1\ 4\ 2)^2 = (1\ 2\ 4)$ and $(2\ 3\ 4)^{-1} = (4\ 3\ 2)$ . So the equation is

$$(1\ 2\ 4)\cdot x = (4\ 3\ 2).$$

Hence,

$$(1\ 2\ 4)^{-1}(1\ 2\ 4)\cdot x = (1\ 2\ 4)^{-1}(4\ 3\ 2), \quad x = (1\ 2\ 4)^{-1}(4\ 3\ 2) = (4\ 2\ 1)(4\ 3\ 2) = (1\ 4\ 3).\quad\halmos$$

Example. ( A permutation which is not a cycle) Show that the following permutation is not a cycle.

$$\left(\matrix{ 1 & 2 & 3 & 4 & 5 \cr 3 & 4 & 5 & 2 & 1 \cr}\right)$$

In fact,

$$\left(\matrix{ 1 & 2 & 3 & 4 & 5 \cr 3 & 4 & 5 & 2 & 1 \cr}\right) = (1\ 3\ 5)(2\ 4).$$

Note that the cycles $(1\ 3\ 5)$ and $(2\ 4)$ are disjoint --- no element is moved by both of them. In fact, an arbitrary permutation may be written as a product of disjoint cycles. Every permutation may also be written as a product of transpositions.

The last example is a particular case of the following theorem.

Theorem. Every permutation on a finite set can be written as a product of disjoint cycles.

Proof. Induct on the number of elements in the set.

First, prove the result for a set with 1 element. This is easy --- there is only one permutation (the identity), and it is the cycle $(1)$ .

Next, assume that the result is known for sets with fewer than n elements and try to prove the result for a set with n elements. Suppose, then, that a permutation on a set with less than n elements can be written as a product of disjoint cycles. I have to show that a permutation on a set with n elements --- that is, an element $\sigma \in S_n$ --- can be written as a product of disjoint cycles.

Since $S_n$ is a finite group, $\sigma$ has finite order. Let m be the order of $\sigma$ . Consider the set

$$Q = \{1, \sigma(1), \sigma^2(1), \ldots, \sigma^{m-1}(1)\}.$$

If $Q = S$ , $\sigma$ is the cycle

$$(1\ \sigma(1)\ \sigma^2(1)\ \ldots \sigma^{m-1}(1)).$$

Otherwise, $Q \ne S$ , so $|S - Q| < n$ .

Now $\sigma$ restricted to $S - Q$ is a permutation on $S - Q$ , so by the inductive assumption it can be written as a product $\tau_1 \tau_2 \cdots \tau_k$ of disjoint cycles. Then

$$\sigma = (1\ \sigma(1)\ \sigma^2(1)\ \ldots \sigma^{m-1}(1)) \tau_1 \tau_2 \cdots \tau_k.$$

Thus, $\sigma$ has been expressed as a product of disjoint cycles. This completes the induction step, and establishes the result for all n.

The proof actually contains an algorithm for decomposing a permutation into a product of disjoint cycles. Start with an element and follow its "orbit" under the permutation until the orbit closes up. If you've exhausted all the elements, you're done. Otherwise, pick an element which wasn't in the orbit of the first element and follow the new element's orbit. Keep going.

Example. ( Writing a permutation as a product of cycles) Write the following permutation as a product of disjoint cycles:

$$\left(\matrix{ 1 & 2 & 3 & 4 & 5 & 6 \cr 6 & 3 & 2 & 1 & 4 & 5 \cr}\right)$$

$$\left(\matrix{ 1 & 2 & 3 & 4 & 5 & 6 \cr 6 & 3 & 2 & 1 & 4 & 5 \cr}\right) = (1\ 6\ 5\ 4)(2\ 3).$$

Here's a picture which shows how I got $(1\ 6\ 5\ 4)$ : 1 goes to 6, which goes to 5, which goes to 4, which goes back to 1.

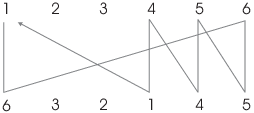
$$\hbox{\epsfysize=1 in \epsffile{permutations-3.eps}}$$

After finishing a cycle, I start with the next element that hasn't been "used" so far. I keep going until all the elements have been accounted for.

If you have a permutation like $\left(\matrix{1 & 2 & 3 \cr 3 & 2 & 1 \cr}\right)$ in which an element doesn't move --- in this case, 2 --- you don't need to write "$(2\ 2)$ ". 2 is simply omitted from the cycle list, since an element which isn't listed doesn't move.

As a general rule, I'll express results of permutation computations as products of disjoint cycles. Note that, for instance, $(1\ 2\ 3) = (2\ 3\ 1) = (3\ 1\ 2)$ , so a given cycle can be written in different ways. You can pick one way by specifying that the first element be the smallest element in the cycle. Moreover, disjoint cycles can be listed in different orders, as the next result shows.

Lemma. Disjoint cycles commute.

Proof. Roughly speaking, if two cycles move different sets of elements, then their effects are independent and it doesn't matter in which order they're applied.

Suppose $\sigma$ and $\tau$ are disjoint cycles:

$$\sigma = (a_1\ a_2\ \ldots a_m) \quad\hbox{and}\quad \tau = (b_1\ b_2\ \ldots b_n).$$

Thus, $\{a_1, a_2, \ldots, a_m\} \cap \{ b_1, b_2, \ldots b_n\} = \emptyset$ .

Then

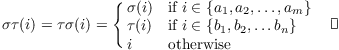
$$\sigma \tau(i) = \tau \sigma(i) = \cases{ \sigma(i) & if $i \in \{a_1, a_2, \ldots, a_m\}$\cr \tau(i) & if $i \in \{ b_1, b_2, \ldots b_n\}$\cr i & otherwise}\quad\halmos$$

Definition. A transposition is a permutation which interchanges two elements and leaves everything else fixed. (That is, a transposition is a cycle of length 2.)

Proposition. Every permutation is a product of transpositions.

Proof. It suffices to show that every cycle is a product of transpositions, since every permutation is a product of cycles. Just observe that

$$(1\ 2\ \ldots n) = (1\ n)\cdots (1\ 3)(1\ 2).$$

To do the same for an arbitrary cycle $(a_1\ a_2\ \ldots a_n)$ , just add a's to the equation above.

Remark. While the decomposition of a permutation into disjoint cycles is unique up to order and representation of the cycles (i.e. $(1\ 2\ 3) = (2\ 3\ 1)$ ), a permutation may be written as a product of transpositions in infinitely many ways. You can always tack on trivial terms of the form $(a\ b)(a\ b) = 1$ .

Example. ( Writing a permutation as a product of transpositions) Express $(2\ 7\ 4\ 5)$ as a product of transpositions in two different ways.

$$(2\ 7\ 4\ 5) = (2\ 5)(2\ 4)(2\ 7) \quad\hbox{and}\quad (2\ 7\ 4\ 5) = (2\ 5)(2\ 4)(2\ 7)(3\ 6)(3\ 6).$$

The decomposition of a permutation into a product of transpositions is not unique.

Lemma. A permutation cannot be written as a product of both an odd and an even number of transpositions.

Proof. Suppose

$$\sigma_1\sigma_2\cdots\sigma_m = \tau_1\tau_2\cdots\tau_n.$$

Assume m is even and n is odd, and all the $\sigma$ 's and $\tau$ 's are transpositions.

Since $\tau_i^{-1} = \tau_i$ ,

$$\tau_n\cdots\tau_2\tau_1\sigma_1\sigma_2\cdots\sigma_m = \id.$$

Note that the identity permutation $\id$ has been written as a product of an odd ($m + n$ ) number of transpositions. If this is impossible, I have a contradiction.

It therefore suffices to show that the identity permutation $\id$ cannot be written as a product of an odd number of transpositions. I'll give a proof by contradiction.

Suppose m is odd and

$$\id = \sigma_1\sigma_2\cdots\sigma_m.$$

Here is a clever idea. Consider a polynomial $f(x_1, \ldots, x_n)$ in n variables. A permutation $\sigma \in S_n$ transforms f into another polynomial by "permuting the variables":

$$\sigma(f) = f(x_{\sigma(1)}, \ldots, x_{\sigma(n)}).$$

For example, suppose $f(x_1, x_2, x_3) = x_1^3 + 3 x_1 x_3 - 5 x_2^7 x_3^4 + 1$ . Suppose $\sigma = (2\ 1\ 3)$ . Then

$$\sigma(f) = x_3^3 + 3 x_3 x_2 - 5 x_1^7 x_2^4 + 1.$$

Now consider the polynomial

$$f(x_1, \ldots, x_n) = \prod_{i > j} (x_i - x_j).$$

For example, if $n = 3$ ,

$$f(x_1, x_2, x_3) = (x_3 - x_1)(x_3 - x_2)(x_2 - x_1).$$

Obviously, the identity permutation takes f to itself.

On the other hand, a transposition $(i\ j)$ for $i > j$ takes the factor $x_i - x_j$ to $x_j - x_i = -(x_i - x_j)$ . In other words, a factor of -1 is introduced for each transposition. Since $\sigma_1\sigma_2\cdots\sigma_m$ contains an odd number of transpositions, it will send f to $(-1)^m f = -f$ .

This is a contradiction: If $\id$ and $\sigma_1\sigma_2\cdots\sigma_m$ are the same permutation, they should have the same effect on f. Therefore, the identity cannot be written as a product of an odd number of transpositions. Hence, a permutation cannot be written as a product of both an even and an odd number of transpositions.

Since the lemma shows that you can't write a given permutation as a product of both an even and an odd number of transpositions, the following definition makes sense.

Definition. A permutation is even if it can be written as a product of an even number of transpositions; a permutation is odd if it can be written as a product of an odd number of transpositions.

Remark. Consider the decomposition

$$(1\ 2\ \ldots n) = (1\ n) \cdots (1\ 3)(1\ 2).$$

This shows that a cycle of length n is an even permutation if n is odd, and is an odd permutation if n is even. For example, the cycle $(6\ 2\ 5)$ is even, since it has length 3 and 3 is odd.

Definition. The alternating group $A_n$ on n letters is the subgroup of $S_n$ consisting of the even permutations.

I should check that $A_n$ really is a subgroup. First, $\id$ is even, so $\id \in A_n$ . Next, if $\sigma$ and $\tau$ are even, then $\tau^{-1}$ is even (decompose $\tau$ into transpositions, and write the product backwards). Therefore, $\sigma \tau^{-1}$ is even (by concatenating decompositions of $\sigma$ and $\tau^{-1}$ into products of transpositions). Hence, $\sigma \tau^{-1} \in A_n$ .

If $n \ge 3$ , there are an equal number of even and odd permutations. Therefore, $(S_n:A_n) = 2$ . In fact, $A_n$ is a normal subgroup of $S_n$ .

Example. List the elements of $A_3$ , the alternating group on 3 letters.

Here is the multiplication table for $S_3$ :

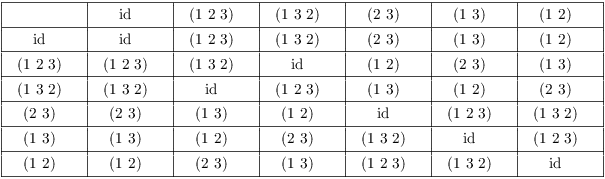
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & $\id$ & & (1\ 2\ 3) & & (1\ 3\ 2) & & (2\ 3) & & (1\ 3) & & (1\ 2) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\id$ & & $\id$ & & (1\ 2\ 3) & & (1\ 3\ 2) & & (2\ 3) & & (1\ 3) & & (1\ 2) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1\ 2\ 3) & & (1\ 2\ 3) & & (1\ 3\ 2) & & $\id$ & & (1\ 2) & & (2\ 3) & & (1\ 3) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1\ 3\ 2) & & (1\ 3\ 2) & & $\id$ & & (1\ 2\ 3) & & (1\ 3) & & (1\ 2) & & (2\ 3) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (2\ 3) & & (2\ 3) & & (1\ 3) & & (1\ 2) & & $\id$ & & (1\ 2\ 3) & & (1\ 3\ 2) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1\ 3) & & (1\ 3) & & (1\ 2) & & (2\ 3) & & (1\ 3\ 2) & & $\id$ & & (1\ 2\ 3) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1\ 2) & & (1\ 2) & & (2\ 3) & & (1\ 3) & & (1\ 2\ 3) & & (1\ 3\ 2) & & $\id$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The alternating group on 3 letters is the "rotation subgroup":

$$A_3 = \{\id, (1\ 2\ 3), (1\ 3\ 2)\}.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2022 by Bruce Ikenaga