Rings

Definition. A ring is an abelian group R with binary operation + ("addition"), together with a second binary operation $\cdot$ ("multiplication"). The operations satisfy the following axioms:

1. Multiplication is associative: For all $a, b, c \in R$ ,

$$(a \cdot b) \cdot c = a \cdot (b \cdot c).$$

2. The Distributive Law holds: For all $a, b, c \in R$ ,

$$a \cdot (b + c) = a \cdot b + a \cdot c \quad\hbox{and}\quad (a + b) \cdot c = a \cdot c + b \cdot c.$$

Remark. 1. To say that R is an abelian group under addition means that the following axioms hold:

(a) (Associativity) $(a + b) + c = a + (b + c)$ for all $a, b, c \in R$ .

(b) (Identity) There is an element $0 \in R$ such that $a + 0 = a$ and $0 + a = a$ for all $a \in R$ .

(c) (Inverses) For all $a \in R$ , there is an element $-a \in R$ such that $a + (-a) = 0$ and $(-a) + a = 0$ .

(d) (Commutativity) $a + b = b + a$ for all $a, b \in R$ .

Definition. A ring R has a multiplicative identity if there is an element $1 \in R$ such that $1 \ne 0$ , and such that for all $a \in R$ ,

$$1 \cdot a = a \quad\hbox{and}\quad a \cdot 1 = a.$$

A ring satisfying this axiom is called a ring with 1, or a ring with identity.

Note that in the term "ring with identity", the word "identity" refers to a multiplicative identity. Every ring has an additive identity ("0") by definition.

Remark. I'll often suppress the multiplication symbol and simply write "$a b$ " for "$a \cdot b$ ". As usual, $a^2$ means $a \cdot a$ , $a^3$ means $a \cdot a \cdot a$ , and so on.

However, note that negative powers of elements are not always defined: An element in a ring might not have a multiplicative inverse. This means that you don't always have "division"; you do have "subtraction", since that's the same as adding the additive inverse.

Many elementary algebraic operations work the way you'd expect. (There will be some surprises later, however.)

Proposition. Let R be a ring.

(a) If $r \in R$ , then $r \cdot 0 = 0 = 0\cdot r$ .

(b) Let $r \in R$ , and let $-r$ denote the additive inverse of r. If R is a ring with identity, then $(-1) \cdot r = -r$ .

(c) Let $r, s \in R$ . Then $(-r) \cdot s = -(r s) = r \cdot (-s)$ .

Proof. (a) Let $r \in R$ . Note that

$$r \cdot 0 = r \cdot (0 + 0) = r \cdot 0 + r \cdot 0.$$

Therefore $0 = r \cdot 0$ .

(b) Suppose R is a ring with identity, and let $r \in R$ . Then

$$(-1) \cdot r + r = (-1) \cdot r + 1 \cdot r = (-1 + 1) \cdot r = 0 \cdot r = 0.$$

Therefore, $(-1) \cdot r$ is the additive inverse of r, i.e. $(-1) \cdot r = -r$ .

(c) The proof is similar to the proof of (b).

Notation. If R is a ring and n is a positive integer, $n r$ is short for $r + r + \cdots r$ (n summands). Likewise, if n is a negative integer, $n r$ is $(-n) r$ . (This is the usual convention for an abelian group.)

Notice that, for example, $13 \cdot 1 \in \integer_6$ makes sense according to this convention: It is 1 added to itself 13 times. However, you should not write "$13 \in \integer_6$ ", since 13 is not an element of $\integer_6$ .

Definition. If R is a ring and $a b = b a$ for all $a, b \in R$ , R is a commutative ring.

Note that the adjective "commutative" applies to the multiplication operation; the addition operation is always commutative by definition.

Example. Which of the following sets are rings under the usual operations? Are they commutative? Do they have an identity element?

$$\integer, \quad 2 \integer, \quad \rational, \quad \rational^+, \quad \real, \quad \complex.$$

$\integer$ is a commutative ring with identity.

$2 \integer$ is a commutative ring, but it does not have an identity.

$\rational$ is a commutative ring with identity.

$\rational^+$ , the set of positive rationals, is not a ring. It does not contain an identity for addition.

$\real$ is a commutative ring with identity.

$\complex$ is a commutative ring with identity.

The ring of quaternions.

The ring of quaternions is the set

$$\quaternion = \{w + x i + y j + z k \mid w, x, y, z \in \real\}.$$

The "H" honors William Rowan Hamilton, who discovered the quaternions in the 1840's.

You add elements in the obvious way, e.g.

$$(2 + 4 i - 9 j + 11 k) + (13 - i + 5 j + 17 k) = 15 + 3 i - 4 j + 28 k.$$

Multiply elements using the following multiplication table:

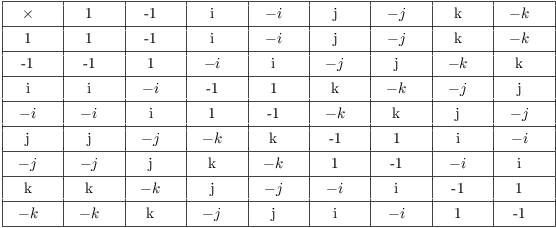
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\times$ & & 1 & & -1 & & i & & $-i$ & & j & & $-j$ & & k & & $-k$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & -1 & & i & & $-i$ & & j & & $-j$ & & k & & $-k$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & -1 & & -1 & & 1 & & $-i$ & & i & & $-j$ & & j & & $-k$ & & k & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & i & & i & & $-i$ & & -1 & & 1 & & k & & $-k$ & & $-j$ & & j & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $-i$ & & $-i$ & & i & & 1 & & -1 & & $-k$ & & k & & j & & $-j$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & j & & j & & $-j$ & & $-k$ & & k & & -1 & & 1 & & i & & $-i$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $-j$ & & $-j$ & & j & & k & & $-k$ & & 1 & & -1 & & $-i$ & & i & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & k & & k & & $-k$ & & j & & $-j$ & & $-i$ & & i & & -1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $-k$ & & $-k$ & & k & & $-j$ & & j & & i & & $-i$ & & 1 & & -1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

(This is the multiplication table for the group of the quaternions Q; in $\quaternion$ , 1, i, j, and k can be multiplied by real numbers as if they were vectors. In fact, ignoring the multiplication, $\quaternion$ is just a 4-dimensional vector space over $\real$ .)

For example,

$$(3 i - 2 k) \cdot (3 + 2 j) = 15 i.$$

$\quaternion$ is a noncommutative ring, since (e.g.) $i j = k$ but $j i = -k$ . In fact, Hamilton apparently was stuck on this point for many years. He knew that complex numbers could be used to represent rotations in two dimensions, and he was trying to construct an algebraic system for representing rotations in three dimensions. The problem is that rotations in three dimensions don't commute, whereas he expected his algebraic system to have a commutative multiplication --- as did all the number systems known up to that time.

Verifying the other ring axioms is routine, but very tedious! We'll add $\quaternion$ to our collection of common number systems, along with the integers, the rationals, the real numbers, and the complex numbers.

Example. ( The integers mod n as rings) Construct a multiplication table for $\integer_3$ . What kind of ring is it?

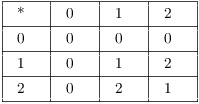
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & * & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 0 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 0 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

For example, $2 \cdot 2 = 1$ , since as integers $2 \cdot 2 = 4$ , and 4 reduces to 1 mod 3.

With these operations, $\integer_3$ becomes a commutative ring with 1.

In general, $\integer_n$ is a commutative ring with 1.

Example. ( A ring without an identity) Prove that the set of even integers $2 \integer$ with the usual operations is a ring without an identity.

Suppose that $e \in 2 \integer$ is an identity. Then $e = 2 n$ for some $n \in \integer$ . Since e is an identity, I must have (for instance)

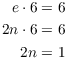
$$\eqalign{ e \cdot 6 & = 6 \cr 2 n \cdot 6 & = 6 \cr 2 n & = 1 \cr}$$

Since there is no integer n for which this is true, $2 \integer$ cannot have an identity.

Example. ( A ring of matrices) $M(2, \real)$ is the set of $2 \times 2$ matrices with real entries. The operations are the usual matrix addition and multiplication. The additive identity is $\displaystyle \left[\matrix{0 & 0 \cr 0 & 0 \cr}\right]$ ; the multiplicative identity is $\displaystyle \left[\matrix{1 & 0 \cr 0 & 1 \cr}\right]$ .

Show by example that $M(2, \real)$ is a noncommutative ring.

$$\left[\matrix{1 & 2 \cr 3 & -1 \cr}\right] \left[\matrix{2 & 1 \cr 4 & 1 \cr}\right] = \left[\matrix{10 & 3 \cr 2 & 2 \cr}\right], \quad\hbox{but}\quad \left[\matrix{2 & 1 \cr 4 & 1 \cr}\right] \left[\matrix{1 & 2 \cr 3 & -1 \cr}\right] = \left[\matrix{5 & 3 \cr 7 & 7 \cr}\right].\quad\halmos$$

Example. ( A ring of functions) $C[0, 1]$ is the set of continuous functions $f: [0,1] \rightarrow \real$ . Operations are pointwise addition and multiplication:

$$(f + g)(x) = f(x) + g(x) \quad\hbox{and}\quad (f g)(x) = f(x) g(x).$$

Is $C[0, 1]$ a commututative ring? What are the additive and multiplicative identities?

$C[0,1]$ is a commutative ring, since by commutativity of real number multiplication,

$$(f g)(x) = f(x) g(x) = g(x) f(x) = (g f)(x).$$

The constant functions 0 and 1 are the additive and multiplicative identities, respectively.

Polynomial rings.

Let R be a commutative ring. $R[x]$ denotes the ring of polynomials in one variable with coefficients in R. Add and multiply polynomials as usual.

For example, $\real[x]$ consists of all polynomials with real coefficients: things like

$$x + 2, \quad 3 - 7 x^2 + 54 x^{17}, \quad 42, \ldots.$$

The formal, precise way to define $R[x]$ is to define it to be the collection of finite ordered n-tuples

$$\{(r_0, r_1, \ldots, r_n) \mid n \ge 0, r_i \in R\}.$$

(That is, a polynomial is the "vector" of its coefficients.) Now you can define addition and multiplication by writing down some ugly, unenlightening formulas. The point of mentioning this is to show that we're not doing something invalid by thinking of polynomials as "formal sums in powers of x" --- you could do things in a perfectly rigorous way if you chose.

Note that polynomials are not functions in this context. For example, let $R = \integer_2$ and look at $f(x) = x^2 + x$ . This is not zero as a polynomial, even though $f(0) = 0$ and $f(1) = 0$ ; i.e., even though it vanishes on every element of the ring.

Contact information

Bruce Ikenaga's Home Page

Copyright 2022 by Bruce Ikenaga