Limit Theorems

In this section, I'll give proofs of some of the properties of limits. This section is pretty heavy on theory --- more than I'd expect people in a calculus course to know. So unless you're reading this section to learn about analysis, you might skip it, or just look at the statements of the results and the examples.

First, let's recall the $\epsilon-\delta$ definition of a limit.

Definition. Let f be a real-valued function defined on an open interval containing a point $c \in \real$ , but possibly not at c. If $L \in \real$ , then $\displaystyle \lim_{x \to c} f(x) = L$ means: For every $\epsilon > 0$ , there is a $\delta$ such that for every x in the domain of f,

$$\hbox{If}\quad \delta > |x - c| > 0, \quad\hbox{then}\quad \epsilon > |f(x) - L|.$$

Informally, "making x close to c makes $f(x)$ close to L". In this section, I'll prove various results for computing limits. But I'll begin with an example which shows that the limit of a function at a point does not have to be defined.

In the next example and in several of the proofs below, I'll need to use the Triangle Inequality. It says that if p and q are real numbers, then

$$|p| + |q| \ge |p + q|.$$

You often use the Triangle Inequality to combine absolute value terms (going from the left side to the right side) or to break up an absolute value term (going from the right side to the left side).

Example. ( A limit that is undefined) Let

$$f(x) = \cases{ 1 & if $x > 0$ \cr -1 & if $x < 0$ \cr}.$$

Prove that

$$\lim_{x \to 0} f(x) \quad\hbox{is undefined}.$$

Suppose on the contrary that

$$\lim_{x \to 0} f(x) = L.$$

This means that for every $\epsilon > 0$ , there is a $\delta$ such that

$$\hbox{If}\quad \delta > |x| > 0, \quad\hbox{then}\quad \epsilon > |f(x) - L|.$$

(In this case, the "c" of the definition is equal to 0.)

Choose $\epsilon = \dfrac{1}{2}$ . I'll that there is no number $\delta$ such that if $\delta > |x| > 0$ , then

$$\dfrac{1}{2} > |f(x) - L|.$$

Suppose there is such a number $\delta$ . The x's which satisfy the inequality $\delta > |x|$ are the points in the interval $-\delta < x < \delta$ . Note that there are both positive and negative numbers in this interval.

Let a be a positive number in $-\delta < x < \delta$ . Since $a > 0$ , I have $f(a) = 1$ , so

$$\dfrac{1}{2} > |f(a) - L| = |1 - L|.$$

Let b be a negative number in $-\delta < x < \delta$ . Since $b < 0$ , I have $f(b) = -1$ , so

$$\dfrac{1}{2} > |f(b) - L| = |-1 - L|.$$

Note that

$$|-1 - L| = |(-1)(1 + L)| = |-1| \cdot |1 + L| = 1 \cdot |1 + L| = |1 + L|.$$

So I can write my two inequalities like this:

$$\dfrac{1}{2} > |1 - L| \quad\hbox{and}\quad \dfrac{1}{2} > |1 + L|.$$

Add the two inequalities:

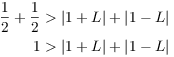
$$\eqalign{ \dfrac{1}{2} + \dfrac{1}{2} & > |1 + L| + |1 - L| \cr 1 & > |1 + L| + |1 - L| \cr}$$

By the Triangle Inequality,

$$|1 + L| + |1 - L| \ge |(1 + L) + (1 - L)| = |2| = 2.$$

Combining this with $1 > |1 + L| + |1 - L|$ , I get

$$1 > |1 + L| + |1 - L| \ge 2, \quad\hbox{or}\quad 1 > 2.$$

This is a contradiction. Therefore, my assumption that $\displaystyle \lim_{x \to 0} f(x)$ is defined must be incorrect, and the limit is undefined.

Proposition. ( The limit of a constant) Let $k \in \real$ and $c \in \real$ . Then

$$\lim_{x \to c} k = k.$$

In other words, the limit of a constant is the constant.

Proof. In this case, the function is $f(x) = k$ and the limit is $L = k$ .

Let $\epsilon > 0$ . Then

$$\epsilon > |k - k| = 0.$$

Since the conclusion of the statement "If $\delta > |x - c| > 0$ , then $\epsilon > |f(x) - L|$ " is true, the statement is true regardless of what $\delta$ is. (For the sake of definiteness, I could choose $\delta = 1$ , for example.) This proves that $\displaystyle \lim_{x \to c} k = k$ .

Proposition. Let $c \in \real$ . Then

$$\lim_{x \to c} x = c.$$

Proof. In this case, the function is $f(x) = x$ and the limit is $L = c$ .

Let $\epsilon > 0$ . Set $\delta = \epsilon$ . Suppose $\delta > |x - c| > 0$ . Since $\delta = \epsilon$ , I have

$$\epsilon > |x - c|.$$

This proves that $\displaystyle \lim_{x \to c} x = c$ .

Theorem. ( The limit of a sum) Let $c \in \real$ . Let f and g be functions defined on an open interval containing c, but possibly not at c. Suppose that

$$\lim_{x \to c} f(x) = L \quad\hbox{and}\quad \lim_{x \to c} g(x) = M.$$

Then

$$\lim_{x \to c} \left[f(x) + g(x)\right] = L + M.$$

Proof. Let $\epsilon > 0$ . I need to find a number $\delta$ such that

$$\hbox{If}\quad \delta > |x - c| > 0, \quad\hbox{then}\quad \epsilon > |\left[f(x) + g(x)\right] - (L + M)|.$$

The idea is that since $\displaystyle \lim_{x \to c} f(x) = L$ , I can force $f(x)$ to be close to L, and since $\displaystyle \lim_{x \to c} g(x) = M$ , I can force $g(x)$ to be close to M. Since I want $f(x) + g(x)$ to be within $\epsilon$ of $L + M$ , I'll split the difference: I'll force $f(x)$ to be within $\dfrac{\epsilon}{2}$ of L and force $g(x)$ to be within $\dfrac{\epsilon}{2}$ of M.

First, $\displaystyle \lim_{x \to c} f(x) = L$ means that I can find a number $\delta_1$ such that

$$\hbox{If}\quad \delta_1 > |x - c| > 0, \quad\hbox{then}\quad \dfrac{\epsilon}{2} > |f(x) - L|.$$

Likewise, $\displaystyle \lim_{x \to c} g(x) = M$ means that I can find a number $\delta_2$ such that

$$\hbox{If}\quad \delta_2 > |x - c| > 0, \quad\hbox{then}\quad \dfrac{\epsilon}{2} > |g(x) - M|.$$

I'd like to choose $\delta$ so that both of these hold. To do this, I'll let $\delta$ be the smaller of $\delta_1$ and $\delta_2$ . (If $\delta_1$ and $\delta_2$ are equal, I choose $\delta$ to be their common value.) The mathematical notation for this is

$$\delta = \min(\delta_1, \delta_2).$$

Since $\delta$ is the smaller of $\delta_1$ and $\delta_2$ , it must be at least as small as both:

$$\delta_1 \ge \delta \quad\hbox{and}\quad \delta_2 \ge \delta.$$

Now suppose $\delta > |x - c| > 0$ . Since $\delta_1 \ge \delta$ ,

$$\delta_1 \ge \delta > |x - c| > 0.$$

Therefore,

$$\dfrac{\epsilon}{2} > |f(x) - L|.$$

Since $\delta_2 \ge \delta$ ,

$$\delta_2 \ge \delta > |x - c| > 0.$$

Therefore,

$$\dfrac{\epsilon}{2} > |g(x) - M|.$$

Add the inequalities $\dfrac{\epsilon}{2} > |f(x) - L|$ and $\dfrac{\epsilon}{2} > |g(x) - M|$ :

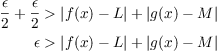
$$\eqalign{ \dfrac{\epsilon}{2} + \dfrac{\epsilon}{2} & > |f(x) - L| + |g(x) - M| \cr \epsilon & > |f(x) - L| + |g(x) - M| \cr}$$

By the Triangle Inequality,

$$|f(x) - L| + |g(x) - M| \ge |(f(x) - L) + (g(x) - M)| = |\left[f(x) + g(x)\right] - (L + M)|.$$

Combining this with $\epsilon > |f(x) - L| + |g(x) - M|$ , I get

$$\epsilon > |\left[f(x) + g(x)\right] - (L + M)|.$$

This proves that $\displaystyle \lim_{x \to c} \left[f(x) + g(x)\right] = L + M$ .

Remark. This result is often written as

$$\lim_{x \to c} \left[f(x) + g(x)\right] = \lim_{x \to c} f(x) + \lim_{x \to c} g(x).$$

But it's important to understand that the equation is true provided that the limits on the right side are defined. If they are not, then the result might be false. For example, let

$$f(x) = \cases{ 1 & if $x > 0$ \cr -1 & if $x < 0$ \cr} \quad\hbox{and}\quad g(x) = \cases{ -1 & if $x > 0$ \cr 1 & if $x < 0$ \cr}.$$

In an earlier example, I showed that $\displaystyle \lim_{x \to 0} f(x)$ is undefined. Since $g(x) = -f(x)$ , essentially the same proof as in the example shows that $\displaystyle \lim_{x \to 0} g(x)$ is undefined. However,

$$f(x) + g(x) = \cases{ 0 & if $x > 0$ \cr 0 & if $x < 0$ \cr}.$$

Hence, the limit-of-a-constant rule shows that

$$\lim_{x \to 0} \left[f(x) + g(x)\right] = \lim_{x \to 0} 0 = 0.$$

In this case, the equation

$$\lim_{x \to c} \left[f(x) + g(x)\right] = \lim_{x \to c} f(x) + \lim_{x \to c} g(x) \quad\hbox{does not hold}.$$

The left side is 0, while the right side is undefined.

Remark. The rule for sums holds for a sum of more than 2 terms. Without writing out all the hypotheses, it says

$$\lim_{x \to a} \left(f_1(x) + f_2(x) + \cdots + f_n(x)\right) = \lim_{x \to a} f_1(x) + \lim_{x \to a} f_2(x) + \cdots + \lim_{x \to a} f_n(x).$$

The proof uses mathematical induction; I won't write it out, though it isn't that difficult. I will, however, use this result in proving the rule for limits of polynomials.

Having just proved a limit rule for sums, it's natural to try to prove a similar rule for products. With the appropriate fine print, it should say that

$$\lim_{x \to c} \left[f(x) \cdot g(x)\right] = [\lim_{x \to c} f(x)] \cdot [\lim_{x \to c} g(x)].$$

If you try to write a proof for this, you might find it a bit more challenging than the ones I've done so far. While it's possible to write a direct proof, some of the ones I've seen look a bit magical: They're shorter than the approach I'll take, but it can be hard to see how someone thought of them.

So instead, I'll take a different approach, which is often useful in writing proofs in math: If your proof looks too difficult, try to prove a special case first. I'll get a bunch of special cases (which are useful in their own rights), and whose proofs are fairly straightforward.

I'll begin with the special case where one of the functions in the product is just a constant.

Theorem. ( Multiplication by constants) Let $k, c \in \real$ . Let f be a function defined on an open interval containing c, but possibly not at c. Suppose that

$$\lim_{x \to c} f(x) = L.$$

Then

$$\lim_{x \to c} [k \cdot f(x)] = k \cdot L.$$

Proof. First, if $k = 0$ , then the limit-of-a-constant rule says

$$\lim_{x \to c} [k \cdot f(x)] = \lim_{x \to c} [0 \cdot f(x)] = \lim_{x \to c} 0 = 0.$$

But $k \cdot L = 0 \cdot L = 0$ , so desired equation holds:

$$\lim_{x \to c} [k \cdot f(x)] = 0 = k \cdot L.$$

Having dealt with the case $k = 0$ , I'll assume $k \ne 0$ .

Let $\epsilon > 0$ . By assumption,

$$\lim_{x \to c} f(x) = L.$$

Hence, I may find $\delta$ so that if $\delta > |x - c| > 0$ , then

$$\dfrac{\epsilon}{|k|} > |f(x) - L|.$$

(Notice that I'm not dividing by 0 on the left side, because $k \ne 0$ .)

With this value of $\delta$ , I have that $\delta > |x - c| > 0$ implies

$$\eqalign{ \dfrac{\epsilon}{|k|} & > |f(x) - L| \cr \noalign{\vskip2pt} \epsilon & > |k| \cdot |f(x) - L| \cr \epsilon & > |[k \cdot f(x)] - (k \cdot L)| \cr}$$

This proves that

$$\lim_{x \to c} [k \cdot f(x)] = k \cdot L.\quad\halmos$$

Remark. This rule is often written more concisely as

$$\lim_{x \to c} [k \cdot f(x)] = k \cdot \lim_{x \to c} f(x).$$

The multiplication-by-constants rule is a special case of the general rule for products that I'd like to prove, but it's useful in its own right. Here are two easy consequences.

Corollary. ( Negatives) Let $c \in \real$ . Let f be a function defined on an open interval containing c, but possibly not at c. Suppose that

$$\lim_{x \to c} f(x) = L.$$

Then

$$\lim_{x \to c} [-f(x)] = -L.$$

Proof. Take $k = -1$ in the multiplication-by-constants rule.

Corollary. ( The limit of a difference) Let $c \in \real$ . Let f and g be functions defined on an open interval containing c, but possibly not at c. Suppose that

$$\lim_{x \to c} f(x) = L \quad\hbox{and}\quad \lim_{x \to c} g(x) = M.$$

Then

$$\lim_{x \to c} \left[f(x) - g(x)\right] = L - M.$$

Proof. By the preceding corollary, I have

$$\lim_{x \to c} [-g(x)] = -M.$$

Therefore, by the rule for sums,

$$\lim_{x \to c} \left[f(x) - g(x)\right] = \lim_{x \to c} \left(f(x) + [-g(x)]\right) = L + (-M) = L - M.\quad\halmos$$

Here's another special case of the limit of a product.

Lemma. ( Product of zero limits) Let $c \in \real$ . Let f and g be functions defined on an open interval containing c, but possibly not at c. Suppose that

$$\lim_{x \to c} f(x) = 0 \quad\hbox{and}\quad \lim_{x \to c} g(x) = 0.$$

Then

$$\lim_{x \to c} \left[f(x) \cdot g(x)\right] = 0.$$

Proof. Let $\epsilon > 0$ . I need to find a number $\delta$ such that

$$\hbox{If}\quad \delta > |x - c| > 0, \quad\hbox{then}\quad \epsilon > |f(x) \cdot g(x)|.$$

The idea is that I can "control" $f(x)$ and $g(x)$ , so I'll try to get two inequalities $A > |f(x)|$ and $B > |g(x)|$ which multiply to $\epsilon > |f(x) \cdot g(x)|$ . Since the problem seems to be "symmetric" in f and g, it's natural to use $A = B = \sqrt{\epsilon}$ .

Since $\displaystyle \lim_{x \to c} f(x) = 0$ , I may find a number $\delta_1$ such that if $\delta_1 > |x - c| > 0$ , then

$$\sqrt{\epsilon} > |f(x)|.$$

Since $\displaystyle \lim_{x \to c} g(x) = 0$ , I may find a number $\delta_2$ such that if $\delta_2 > |x - c| > 0$ , then

$$\sqrt{\epsilon} > |g(x)|.$$

Now let $\delta = \min(\delta_1, \delta_2)$ . Then if $\delta > |x - c| > 0$ , I have both $\delta_1 > |x - c| > 0$ and $\delta_2 > |x - c| > 0$ . Thus,

$$\sqrt{\epsilon} > |f(x)| \quad\hbox{and}\quad \sqrt{\epsilon} > |g(x)|.$$

Multiplying the last two inequalities, I get

$$\epsilon > |f(x) \cdot g(x)|.$$

This proves that $\displaystyle \lim_{x \to c} \left[f(x) \cdot g(x)\right] = 0$ .

You can consider the next lemma an example of how you might use the preceding results.

Lemma. Let $c \in \real$ . Let f be a function defined on an open interval containing c, but possibly not at c. Suppose that

$$\lim_{x \to c} f(x) = L.$$

Then

$$\lim_{x \to c} [f(x) - L] = 0.$$

Proof.

$$\matrix{ \lim_{x \to c} [f(x) - L] & = & \lim_{x \to c} f(x) - \lim_{x \to c} L & \hbox{(Limit of a difference)} \hfil \cr & = & L - L & \hbox{(Given limit, limit of a constant)} \hfil \cr & = & 0 & \cr} \quad\halmos$$

Now I'll put together a lot of the previous results to prove the rule for the limit of a product. I actually don't need an $\epsilon-\delta$ proof in this case: Just the earlier rules and some careful algebra.

Theorem. ( The limit of a product) Let $c \in \real$ . Let f and g be functions defined on an open interval containing c, but possibly not at c. Suppose that

$$\lim_{x \to c} f(x) = L \quad\hbox{and}\quad \lim_{x \to c} g(x) = M.$$

Then

$$\lim_{x \to c} \left[f(x) \cdot g(x)\right] = L \cdot M.$$

Proof. Suppose that

$$\lim_{x \to c} f(x) = L \quad\hbox{and}\quad \lim_{x \to c} g(x) = M.$$

By the last lemma,

$$\lim_{x \to c} (f(x) - L) = 0 \quad\hbox{and}\quad \lim_{x \to c} (g(x) - M) = 0.$$

I apply the product of zero limits lemma and multiply out the factors in the limit:

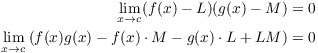
$$\eqalign{ \lim_{x \to c} (f(x) - L)(g(x) - M) & = 0 \cr \lim_{x \to c} \left(f(x) g(x) - f(x) \cdot M - g(x) \cdot L + L M\right) & = 0 \cr}$$

(Save this huge expression for a second.)

Now by the rules for multiplication by constants and the limit of a constant,

$$\lim_{x \to c} f(x) \cdot M = L M, \quad \lim_{x \to c} g(x) \cdot L = L M, \quad \lim_{x \to c} L M = L M.$$

By the rules for the limit of a sum and a difference,

$$\lim_{x \to c} \left(f(x) \cdot M + g(x) \cdot L - L M\right) = L M + L M - L M = L M.$$

So again by the rule for the limit of a sum (I'm adding the big expression in the line above, and the big expression two lines above),

$$\lim_{x \to c} \left[\left(f(x) g(x) - f(x) \cdot M - g(x) \cdot L + L M\right) + \left(f(x) \cdot M + g(x) \cdot L - L M\right)\right] =$$

$$\lim_{x \to c} \left(f(x) g(x) - f(x) \cdot M - g(x) \cdot L + L M\right) + \lim_{x \to c} \left(f(x) \cdot M + g(x) \cdot L - L M\right) = 0 + L M = L M.$$

But (cancelling 6 terms)

$$\lim_{x \to c} \left[\left(f(x) g(x) - f(x) \cdot M - g(x) \cdot L + L M\right) + \left(f(x) \cdot M + g(x) \cdot L - L M\right)\right] = \lim_{x \to c} f(x) g(x).$$

So

$$\lim_{x \to c} f(x) g(x) = L M.\quad\halmos$$

Remark. I had to be careful in using the rule for the limit of a sum to ensure that the component limits were defined before applying the rule. That is why I couldn't simply apply it to the left side of

$$\lim_{x \to c} \left(f(x) g(x) - f(x) \cdot M - g(x) \cdot L + L M\right) = 0.$$

To apply the sum rule to the left side, I would need to know that $\displaystyle \lim_{x \to c} f(x) g(x)$ exists, but that is part of what I was trying to prove.

You might want to look up the shorter, "magical" proofs of the rule for the Limit of a Product and see if you like them better than this approach.

Remark. The rule for products holds for a product of more than 2 terms. Without writing out all the hypotheses, it says

$$\lim_{x \to a} \left(f_1(x) \cdot f_2(x) \cdots f_n(x)\right) = \left(\lim_{x \to a} f_1(x)\right) \cdot \left(\lim_{x \to a} f_2(x)\right) \cdots \left(\lim_{x \to a} f_n(x)\right).$$

The proof uses mathematical induction; I won't write it out, though it isn't that difficult.

My next goal is to prove that if $p(x)$ is a polynomial, then

$$\lim_{x \to a} p(x) = p(a).$$

I'll prove it by putting together some preliminary results. Let's start with a really easy one.

Lemma.

$$\lim_{x \to a} x = a.$$

Proof. Let $\epsilon > 0$ . I have to find $\delta$ so that if $\delta > |x - a| > 0$ , then $\epsilon > |x - a|$ . Just take $\delta = \epsilon$ . Then

$$\delta = \epsilon > |x - a| > 0 \quad\hbox{obviously implies}\quad \epsilon > |x - a|.\quad\halmos$$

Proposition. ( Powers) If n is an integer and $n \ge 0$ , then

$$\lim_{x \to a} x^n = a^n.$$

This proof will use mathematical induction. Explaining induction here would require a separate and fairly lengthy discussion, so I'll just give the proof and assume that you've seen induction elsewhere. Or you can just take this result for granted, since it's not very surprising.

Proof. For $n = 0$ , the left side is (by the constants rule)

$$\lim_{x \to a} x^0 = \lim_{x \to a} 1 = 1.$$

The right side is $a^0 = 1$ . The left and right sides are equal, and the result is true for $n = 0$ .

Assume that $n > 0$ and the result holds for n:

$$\lim_{x \to a} x^n = a^n.$$

I will prove it for $n + 1$ :

$$\lim_{x \to a} x^{n + 1} = \lim_{x \to a} x^n \cdot x = \left(\lim_{x \to a} x^n\right) \left(\lim_{x \to a} x\right) = a^n \cdot a = a^{n + 1}.\quad\halmos$$

The first and last equalities just used rules for powers. The second equality used the rule for the limit of a product. The third equality used the induction assumption and the previous lemma.

This proves the result for $n + 1$ , so the result holds for all $n \ge 0$ by induction.

Remark. The rule for powers holds for negative integer powers. It also holds for rational number powers (with suitable restrictions --- you can't take the square root of a negative number, for instance) and even real number powers. I'll prove some of this below, but the there's an easier way to do all of these at once The idea is that if r is a real number, I can write

$$x^r = e^{r \ln x}.$$

Then I'll need to use limit results on the natural log and exponential functions. That will require a discussion of those functions, which we'll have later.

Theorem. ( Polynomials) Let $a_n$ , $a_{n - 1}$ , ... $a_1$ , $a_0$ be real numbers. Consider the polynomial

$$a_n x^n + a_{n - 1} x^{n - 1} + \cdots + a_1 x + a_0.$$

Then

$$\lim_{x \to c} (a_n x^n + a_{n - 1} x^{n - 1} + \cdots + a_1 x + a_0) = a_n c^n + a_{n - 1} c^{n - 1} + \cdots + a_1 c + a_0.$$

In other words, if $p(x)$ is a polynomial, then

$$\lim_{x \to c} p(x) = p(c).$$

Proof. By the rules for multiplication by constants and powers, for $k = 0$ , ... n, I have

$$\lim_{x \to c} a_k x^k = a_k c^k.$$

Then by the rule for sums (which I remarked holds for a sum with any number of terms),

$$\lim_{x \to c} (a_n x^n + a_{n - 1} x^{n - 1} + \cdots + a_1 x + a_0) = a_n c^n + a_{n - 1} c^{n - 1} + \cdots + a_1 c + a_0.\quad\halmos$$

Example. Compute $\displaystyle \lim_{x \to 3} (2 x^2 + 7 x + 11)$ .

By the rule for polynomials, I can just plug 3 in for x:

$$\lim_{x \to 3} (2 x^2 + 7 x + 11) = 2 \cdot 3^2 + 7 \cdot 3 + 11 = 18 + 21 + 11 = 50.\quad\halmos$$

We'll see that other functions have the property that you can compute $\displaystyle \lim_{x \to c} f(x)$ by "plugging in c for x". The property is called continuity.

You might expect that there would be a rule that says "the limit of a quotient is the quotient of the limits". There is --- though we have to be careful that the component limits exist, and also that we avoid division by 0. As with the rule for products, you can give a proof which looks a little "magical" --- but instead, as I did with the rule for products, I'll derive the rule for quotients from some other rules which are independently useful. There's still a little "magic" in the proof of the lemma for $\displaystyle \lim_{x \to c} \dfrac{1}{x}$ , but it's not too bad if you work backwards "on scratch paper" first.

Lemma. Suppose that $c \ne 0$ . Then

$$\lim_{x \to c} \dfrac{1}{x} = \dfrac{1}{c}.$$

Proof. ( Scratch work.) Before I do the real proof, I do some scratch work so the actual work doesn't seem too magical. This is going to get a little wordy, so if you're not interested, you could just skip to the real proof below.

As is common with limit proofs, I work backwards from what I want. According to the $\epsilon-\delta$ definition, I want

$$\epsilon > \left|\dfrac{1}{x} - \dfrac{1}{c}\right|.$$

Now $\delta > |x - c| > 0$ , so $\delta$ "controls" $|x - c|$ . I'll do some algebra to try to get a factor of $|x - c|$ :

$$\epsilon > \left|\dfrac{1}{x} - \dfrac{1}{c}\right| = \left|\dfrac{c}{c x} - \dfrac{x}{c x}\right| = \left|\dfrac{c - x}{c x}\right| = \dfrac{1}{|c|} \dfrac{1}{|x|} |c - x| = \dfrac{1}{|c|} \dfrac{1}{|x|} |x - c|.$$

I combined the fractions over a common denominator, then broke the result up into three factors. Note that $|c - x| = |x - c|$ , because the absolute value of a number equals the absolute value of its negative.

The first factor $\dfrac{1}{|c|}$ is a constant, so I don't need to worry about it. The third factor is $|x - c|$ , which I can control using $\delta$ .

In order to get some control over the second factor $\dfrac{1}{|x|}$ , I make a preliminary setting of $\delta$ . This isn't a problem, since intuitively I have complete control over $\delta$ . (You'll see how this works out in the real proof.) But how should I set $\delta$ ?

I don't want $\dfrac{1}{|x|}$ to get too big. But if x is close to 0, then $\dfrac{1}{|x|}$ will be large --- for example, $\dfrac{1}{0.001} = 1000$ . So I want to set $\delta$ so that x doesn't get too close to 0.

$\delta$ controls how close x is to c. And I'm given that $c \ne 0$ . So by forcing x to be close enough to c, I can force x to stay away from 0. There are lots of ways to do this; this picture shows what I will do.

$$\hbox{\epsfxsize=2in \epsffile{limit-theorems-1.eps}}$$

As the picture shows, I'll force x to stay within $\dfrac{1}{2} |c|$ of c. I can do this by setting $\delta = \dfrac{1}{2} |c|$ .

There are two cases, depending on whether c is positive or negative, but you can see the cases are symmetric. x will lie in an interval around c, and it won't get any closer to 0 than $\dfrac{1}{2} c$ . Thus,

$$|x| > \dfrac{1}{2} |c|.$$

Taking reciprocals,

$$\dfrac{1}{|x|} < \dfrac{2}{|c|}.$$

Now putting this back into the expression above,

$$\dfrac{1}{|c|} \dfrac{1}{|x|} |x - c| < \dfrac{1}{|c|} \dfrac{2}{|c|} |x - c|.$$

I want the left-hand expression to be less than $\epsilon$ . If the right-hand expression is less than $\epsilon$ , this will be true:

$$\dfrac{1}{|c|} \dfrac{1}{|x|} |x - c| < \dfrac{1}{|c|} \dfrac{2}{|c|} |x - c| < \epsilon.$$

So how can I make $\dfrac{1}{|c|} \dfrac{2}{|c|} |x - c| < \epsilon$ ? Moving the first two terms to the right, I get

$$|x - c| < \dfrac{|c|^2}{2} \epsilon.$$

But I can control $|x - c|$ directly using $\delta$ , so I can make this happen if $\delta = \dfrac{|c|^2}{2} \epsilon$ .

Now earlier, I made a preliminary setting of $\delta = \dfrac{1}{2} |c|$ . I seem to have two settings for $\delta$ . There is a standard trick for getting both of these at once: Set $\delta$ to the smaller of the two. The notation for this is

$$\delta = \min \left(\dfrac{1}{2} |c|, \dfrac{|c|^2}{2} \epsilon\right).$$

Since $\delta$ is the smaller of the two, I get

$$\dfrac{1}{2} |c| \ge \delta > |x - c| \quad\hbox{and}\quad \dfrac{|c|^2}{2} \epsilon \ge \delta > |x - c|.$$

I arrived at my guess for $\delta$ by working backwards. I have to write the real proof forwards, starting with my guess for $\delta$ . Here it is.

( Real proof.) Let $\epsilon > 0$ . Set $\delta = \min \left(\dfrac{1}{2} |c|, \dfrac{1}{2} |c|^2 \epsilon\right)$ . Suppose $\delta > |x - c| > 0$ . Then

$$\dfrac{1}{2} |c| \ge \delta > |x - c| \quad\hbox{and}\quad \dfrac{|c|^2}{2} \epsilon \ge \delta > |x - c|.$$

Consider the first inequality $\dfrac{1}{2} |c| \ge \delta > |x - c|$ . This means that x is less than $\dfrac{1}{2} |c|$ from c. So if c is positive, then

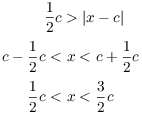
$$\eqalign{ \dfrac{1}{2} c & > |x - c| \cr \noalign{\vskip2pt} c - \dfrac{1}{2} c < &\ x < c + \dfrac{1}{2} c \cr \noalign{\vskip2pt} \dfrac{1}{2} c < &\ x < \dfrac{3}{2} c \cr}$$

And if c is negative, then $\dfrac{1}{2} |c| = \dfrac{1}{2} (-c)$ , so

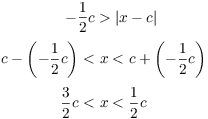
$$\eqalign{ -\dfrac{1}{2} c & > |x - c| \cr \noalign{\vskip2pt} c - \left(-\dfrac{1}{2} c\right) < &\ x < c + \left(-\dfrac{1}{2} c\right) \cr \noalign{\vskip2pt} \dfrac{3}{2} c < &\ x < \dfrac{1}{2} c \cr}$$

$$\hbox{\epsfxsize=2in \epsffile{limit-theorems-1.eps}}$$

In both cases,

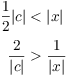
$$\eqalign{ \dfrac{1}{2} |c| & < |x| \cr \noalign{\vskip2pt} \dfrac{2}{|c|} & > \dfrac{1}{|x|} \cr}$$

Multiply $\dfrac{2}{|c|} > \dfrac{1}{|x|}$ and $\dfrac{|c|^2}{2} \epsilon > |x - c|$ to get

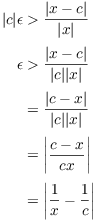
$$\eqalign{ |c| \epsilon & > \dfrac{|x - c|}{|x|} \cr \noalign{\vskip2pt} \epsilon & > \dfrac{|x - c|}{|c| |x|} \cr \noalign{\vskip2pt} & = \dfrac{|c - x|}{|c| |x|} \cr \noalign{\vskip2pt} & = \left|\dfrac{c - x}{c x}\right| \cr \noalign{\vskip2pt} & = \left|\dfrac{1}{x} - \dfrac{1}{c}\right| \cr}$$

This proves that $\displaystyle \lim_{x \to c} \dfrac{1}{x} = \dfrac{1}{c}$ .

The next theorem is important in its own right.

Theorem. ( Composites) Let $a \in \real$ . Suppose that:

(a) f is a function defined on an open interval containing a, but possibly not at a.

(b) $\displaystyle \lim_{x \to a} f(x) = b$ .

(c) g is a function defined on an open interval containing b, but possibly not at b.

(d) $\displaystyle \lim_{x \to b} g(x) = c$ .

Then

$$\lim_{x \to a} g(f(x)) = c.$$

To write it somewhat roughly,

$$\lim_{x \to a} g(f(x)) = \lim_{x \to b} g \left(\lim_{x \to a} f(x)\right).$$

Proof. Let $\epsilon > 0$ . Since $\displaystyle \lim_{x \to b} g(x) = c$ , I can find a number $\gamma$ such that if $\gamma > |x - b| > 0$ , then $\epsilon > |g(x) - c|$ .

Since $\displaystyle \lim_{x \to a} f(x) = b$ , I can find a number $\delta$ such that if $\delta > |x - a| > 0$ , then $\gamma > |f(x) - b|$ .

Suppose that $\delta > |x - a| > 0$ . Then $\gamma > |f(x) - b|$ . But then

$$\epsilon > |g(f(x)) - c|.$$

This proves that $\displaystyle \lim_{x \to a} g(f(x)) = c$ .

Example. Compute $\displaystyle \lim_{x \to 2} (x^3 + 3 x - 1)^4$ .

Let

$$f(x) = x^3 + 3 x - 1 \quad\hbox{and}\quad g(x) = x^4.$$

Then

$$g(f(x)) = (x^3 + 3 x - 1)^4.$$

By the rules for limits of polynomials and composites,

$$\lim_{x \to 2} (x^3 + 3 x - 1)^4 = (2^3 + 3 \cdot 2 - 1)^4 = 13^4 = 28561.\quad\halmos$$

Theorem. ( Reciprocals) Suppose f is a function defined on an open interval containing a, but possibly not at a, and

$$\lim_{x \to a} f(x) = L \ne 0.$$

Then

$$\lim_{x \to a} \dfrac{1}{f(x)} = \dfrac{1}{L}.$$

Proof. Let $g(x) = \dfrac{1}{x}$ . Then

$$\dfrac{1}{f(x)} = g(f(x)).$$

Since $L \ne 0$ , it follows that g is defined on an open interval containing L,

Since $L \ne 0$ , the $\dfrac{1}{x}$ -lemma implies that

$$\lim_{x \to L} g(x) = \lim_{x \to L} \dfrac{1}{x} = \dfrac{1}{L}.$$

Then the rule for composites implies that

$$\lim_{x \to a} g(f(x)) = \lim_{x \to a} \dfrac{1}{f(x)} = \dfrac{1}{L}.\quad\halmos$$

Theorem. ( Quotients) Suppose f and g are functions defined on an open interval containing a, but possibly not at a. Suppose that

$$\lim_{x \to a} f(x) = L \quad\hbox{and}\quad \lim_{x \to a} g(x) = M \ne 0.$$

Then

$$\lim_{x \to a} \dfrac{f(x)}{g(x)} = \dfrac{L}{M}.$$

Proof. Note that $\dfrac{f(x)}{g(x)} = f(x) \cdot \dfrac{1}{g(x)}$ , and that by the reciprocal rule

$$\lim_{x \to a} \dfrac{1}{g(x)} = \dfrac{1}{M}.$$

Then by the rule for products,

$$\lim_{x \to a} \dfrac{f(x)}{g(x)} = L \cdot \dfrac{1}{M} = \dfrac{L}{M}.\quad\halmos$$

Example. Compute $\displaystyle \lim_{x \to 4} \dfrac{7 x + 1}{x^2 + 3}$ .

By the rules for limits of polynomials and quotients,

$$\lim_{x \to 4} \dfrac{7 x + 1}{x^2 + 3} = \dfrac{7 \cdot 4 + 1}{4^2 + 3} = \dfrac{29}{19}.\quad\halmos$$

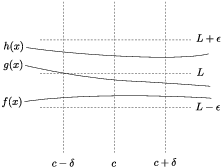
The next result is different from the previous results, in that the statement doesn't seem obvious at first glance. However, the conclusion is reasonable if you draw a picture

Theorem. ( The Squeezing Theorem) Suppose $f(x)$ , $g(x)$ , and $h(x)$ are defined on a open interval I containing c, but are not necessarily defined at c. Assume that

$$f(x) \le g(x) \le h(x) \quad\hbox{for all}\quad x \in I,$$

$$\lim_{x \to c} f(x) = L, \quad \lim_{x \to c} h(x) = L.$$

Then

$$\lim_{x \to c} g(x) = L.$$

Here's a picture which makes the result reasonable:

$$\hbox{\epsfysize=1.5in \epsffile{limit-theorems-2.eps}}$$

The theorem says that if g is caught between f and h, and if f and h both approach a limit L, then g is "squeezed" to the same limit L.

This result is sometimes called the Sandwich Theorem, the idea being that g is the filling of the sandwich and it's caught between the two slices of bread (f and h).

Proof. Let $\epsilon > 0$ .

Since $\displaystyle \lim_{x \to c} f(x) = L$ , I can find $\delta_1$ so that $\delta_1 > |x - c| > 0$ implies

$$\epsilon > |f(x) - L|.$$

Since $\displaystyle \lim_{x \to c} h(x) = L$ , I can find $\delta_2$ so that $\delta_2 > |x - c| > 0$ implies

$$\epsilon > |h(x) - L|.$$

Let $\delta = \min (\delta_1, \delta_2)$ . Thus, $\delta_1 \ge \delta$ and $\delta_2 \ge \delta$ .

Thus, if $\delta > |x - c| > 0$ , then

$$\delta_1 \ge \delta > |x - c| > 0 \quad\hbox{and}\quad \delta_2 \ge \delta > |x - c| > 0.$$

Therefore,

$$\epsilon > |f(x) - L| \quad\hbox{and}\quad \epsilon > |h(x) - L|.$$

Now $\epsilon > |f(x) - L|$ means $f(x)$ is less than $\epsilon$ from L, so

$$f(x) > L - \epsilon.$$

And $\epsilon > |h(x) - L|$ means that $h(x)$ is less than $\epsilon$ from L, so

$$L + \epsilon > h(x).$$

$$\hbox{\epsfysize=1.5in \epsffile{limit-theorems-3.eps}}$$

Hence,

$$L + \epsilon > h(x) \ge g(x) \ge f(x) > L - \epsilon.$$

Therefore,

$$\epsilon > |g(x) - L|.\quad\halmos$$

Example. Prove that $\displaystyle \lim_{x \to 0} x^4 \sin \dfrac{1}{x} = 0$ .

Note that as $x \to 0$ the expression $\sin \dfrac{1}{x}$ is undefined. So, for instance, you can't use the rule for the limit of a product.

From trigonometry, $-1 \le \sin \theta \le 1$ for all $\theta$ . So

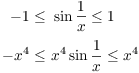
$$\eqalign{ -1 \le &\ \sin \dfrac{1}{x} \le 1 \cr \noalign{\vskip2pt} -x^4 \le &\ x^4 \sin \dfrac{1}{x} \le x^4 \cr}$$

(Note that since $x^4 \ge 0$ , multiplying the inequality by $x^4$ does not cause the inequality to "flip".) Now

$$\lim_{x \to 0} (-x^4) = 0 \quad\hbox{and}\quad \lim_{x \to 0} x^4 = 0.$$

By the Squeezing Theorem,

$$\lim_{x \to 0} x^4 \sin \dfrac{1}{x} = 0.\quad\halmos$$

The next result doesn't seem to have a standard name, so I'll call it The Neighborhood Theorem. It says that the value of $\displaystyle \lim_{x \to c} f(x)$ depends on the values of $f(x)$ near c, not at c. I'll often use this result in computing limits involving indeterminate forms.

In many presentations of calculus, this result isn't stated explicitly. Instead, you'll see it used in the middle of computations like this:

$$\hbox{``}\lim_{x \to 1} \dfrac{(x - 1)(x + 1)}{x - 1} = \lim_{x \to 1} (x + 1).\hbox{''}$$

Note that you can only cancel the $x - 1$ terms if you know $x - 1 \ne 0$ , i.e. if $x \ne 1$ . The author will justify this by saying something like: "We can cancel the $x - 1$ terms because in taking the limit, we only consider x's near 1, rather than $x = 1$ ."

The Neighborhood Theorem applies to this situation in this way: the functions $f(x) = \dfrac{(x - 1)(x + 1)}{x - 1}$ and $g(x) = x + 1$ are equal for all x except $x = 1$ . Therefore, the Neighborhood Theorem says that they have the same limit as x approaches 1.

Theorem. ( The Neighborhood Theorem) Suppose that:

(a) $a < c < b$ .

(b) $f(x) = g(x)$ for all x in the interval $(a, b)$ except possibly at c.

Then the limits $\displaystyle \lim_{x \to c} f(x)$ and $\displaystyle \lim_{x \to c} g(x)$ are either both defined or both undefined. If they are both defined, then they have the same value.

In other words, if two functions are equal in a neighborhood of c, except possibly at c, then they have the same limit at c.

Proof. Suppose that $a < c < b$ and $f(x) = g(x)$ for all x in the interval $(a, b)$ except possibly at c.

Suppose first that $\displaystyle \lim_{x \to c} f(x)= L$ . I will show that $\displaystyle \lim_{x \to c} g(x)= L$ .

Let $\epsilon > 0$ . I must find $\delta$ such that if $\delta > |x - c| > 0$ , then $\epsilon > |g(x) - L|$ .

Since $\displaystyle \lim_{x \to c} f(x)= L$ , the limit definition produces a $\delta$ such that if $\delta > |x - c| > 0$ , then $\epsilon > |f(x) - L|$ . So take this $\delta$ , and suppose that $\delta > |x - c| > 0$ . By the choice of $\delta$ , I get

$$\epsilon > |f(x) - L|.$$

But notice that my assumption $\delta > |x - c| > 0$ includes the assumption that $|x - c| > 0$ . In particular, $x \ne c$ , since if $x = c$ , then $|x - c| = 0$ . Since $x \ne c$ , I have $f(x) = g(x)$ , so

$$\epsilon > |f(x) - L| = |g(x) - L|.$$

This proves that $\displaystyle \lim_{x \to c} g(x)= L$ .

The remaining case is that $\displaystyle \lim_{x \to c} f(x)$ is undefined. In this case, I must show that $\displaystyle \lim_{x \to c} g(x)$ is undefined. Suppose not. Then $\displaystyle \lim_{x \to c} g(x)$ is defined so $\displaystyle \lim_{x \to c} g(x) = L$ for some number L. But then the first part of the proof (with the roles of $f(x)$ and $g(x)$ switched) shows that $\displaystyle \lim_{x \to c} f(x)= L$ . This contradicts my assumption that $\displaystyle \lim_{x \to c} f(x)$ is undefined.

Hence, $\displaystyle \lim_{x \to c} g(x)$ is undefined.

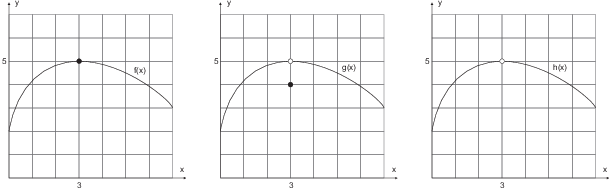
The functions $f(x)$ , $g(x)$ , and $h(x)$ which are graphed below are equal for all x except $x = 3$ . By the Neighborhood Theorem, the three functions have the same limit as x approaches 3:

$$\lim_{x \to 3} f(x) = \lim_{x \to 3} g(x) = \lim_{x \to 3} h(x) = 5.$$

$$\hbox{\epsfysize=1.7in \epsffile{limit-theorems-4a.eps}} \hskip0.25in \hbox{\epsfysize=1.7in \epsffile{limit-theorems-4b.eps}} \hskip0.25in \hbox{\epsfysize=1.7in \epsffile{limit-theorems-4c.eps}}$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2024 by Bruce Ikenaga