Arc Length in Rn

Let $f: [a, b] \to \real^n$ be a curve in $\real^n$ . How would you find the length of the curve? One approach is to start by approximating the curve with segments.

Divide the base interval $[a, b]$ up into subintervals:

$$a_0 = a,\ a_1,\ a_2,\ \ldots a_{n - 1},\ a_n = b.$$

This is called a partition of the subinterval. You may recall doing this to set up Riemann sums.

If you plug the a's into f, you get points on the curve which you can connect with segments. Here's a pictures with 4 points and 3 segments:

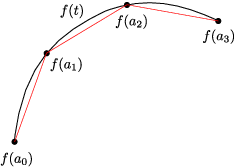
$$\hbox{\epsfysize=1.5in \epsffile{arc-length-in-rn-1.eps}}$$

The sum of the segments lengths approximates the length of the curve.

Definition. A curve $f: [a, b] \to \real^n$ is rectifiable if the sums of the segment lengths have an upper bound: that is, there is a number M such that for every partitition of $[a, b]$ , the sum of the segment lengths is less than M.

If a curve is rectifiable, the length of the curve is least upper bound of the numbers M which bound the sums of segment lengths for all partititions.

If a curve has reasonable properties, we can compute the length using an integral.

Theorem. Suppose $f: [a, b] \to \real^n$ is a curve where f is differentiable and $f'(t)$ is continuous. Then f is rectifiable, and the length of f is

$$\int_a^b \|f'(t)\|\,dt.\quad\halmos$$

While the proof is a little technical, we can see why this makes sense. $\|f'(t)\|$ is the speed of an object moving along the curve. In a small increment $\Delta t$ of time, the object moves a distance $\|f'(t)\|\, \Delta t$ . If we let the time increments go to 0 and add up the distances by integrating, we get the distance travelled by the object, which is the length of the curve.

Example. Find the length of the curve

$$x = t^2 - t, \quad y = \sqrt{3} t^2, \quad z = \dfrac{2 \sqrt{12}}{3} t^{3/2} + 1, \quad\hbox{for}\quad 0 \le t \le 1.$$

$$\der x t = 2 t - 1, \quad \der y t = 2 \sqrt{3} t, \quad \der z t = \sqrt{12} t^{1/2}.$$

$$\left(\der x t\right)^2 = 4 t^2 - 4 t + 1, \quad \left(\der y t\right)^2 = 12 t^2, \quad \left(\der z t\right)^2 = 12 t.$$

$$\left(\der x t\right)^2 + \left(\der y t\right)^2 + \left(\der z t\right)^2 = 16 t^2 + 8 t + 1 = (4 t + 1)^2.$$

$$\sqrt{\left(\der x t\right)^2 + \left(\der y t\right)^2 + \left(\der z t\right)^2} = 4 t + 1.$$

The length is

$$\int_0^1 (4 t + 1)\,dt = \left[2 t^2 + t\right]_0^1 = 3.\quad\halmos$$

Example. Find the length of the curve

$$x = e^{2 t}, \quad y = e^{-2 t}, \quad z = \sqrt{8} t, \quad\hbox{for}\quad 0 \le t \le 1.$$

$$\der x t = 2 e^{2 t}, \quad \der y t = -2 e^{-2 t}, \quad der z t = \sqrt{8}.$$

$$\left(\der x t\right)^2 = 4 e^{4 t}, \quad \left(\der y t\right)^2 = 4 e^{-4 t}, \quad \left(\der z t\right)^2 = 8.$$

$$\left(\der x t\right)^2 + \left(\der y t\right)^2 + \left(\der z t\right)^2 = 4 e^{4 t} + 8 + 4 e^{-4 t} = 4(e^{4 t} + 2 + e^{-4 t}) = 4 (e^{2 t} + e^{-2 t})^2.$$

$$\sqrt{\left(\der x t\right)^2 + \left(\der y t\right)^2 + \left(\der z t\right)^2} = 2 (e^{2 t} + e^{-2 t}).$$

The length is

$$\int_0^1 2 (e^{2 t} + e^{-2 t})\,dt = \left[e^{2 t} - e^{-2 t}\right]_0^1 = e^2 - e^{-2} = 7.25372 \ldots.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga