Center of Mass

Imagine two weights on opposite sides of a balance board. One weight is 5 kilograms and is 4 meters from the center. The other weight is 10 kilograms and is 2 meters from the center.

$$\hbox{\epsfysize=1in \epsffile{center-of-mass-1.eps}}$$

The weights balance. What is relevant is the products of the mass and the distance of the mass from the center.

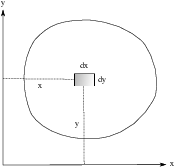
Consider region R in the plane. Imagine that it is made out of a thin material with varying density $\delta(x, y)$ . Consider a small rectangular piece with dimensions $dx$ by $dy$ located at the point $(x, y)$ . Its mass is $\delta(x, y)\,dx\,dy$ .

$$\hbox{\epsfysize=1.5in \epsffile{center-of-mass-2.eps}}$$

The total mass is

$$M = \dint_R \delta(x, y)\,dx\,dy.$$

By analogy with the balance board example, I measure the "twisting" about the y-axis produced by the small rectangular piece. It is the product of the mass $\delta(x, y)\,dx\,dy$ and the distance to the y-axis, which is x:

$$x \cdot d(x, y)\,dx\,dy.$$

The total amount of"twisting" about the y-axis is the x-moment, and is obtained by integrating ("adding up") the "twisting" produced by each of the small pieces that make up the region:

$$m_x = \dint_R x \delta(x, y)\,dx\,dy.$$

I can define the y-moment in the same way:

$$m_y = \dint_R y \delta(x, y)\,dx\,dy.$$

Now imagine the region compressed to small ball which has the same total mass M as the original region. Where should the small ball be located so that it produces the same x and y-moments? The location is called the center of mass of the original region; if its coordinates are $(\overline{x}, \overline{y})$ , I want

$$\overline{x} \cdot M = m_x \quad\hbox{and}\quad \overline{y} \cdot M = m_y.$$

Solving for $\overline{x}$ and $\overline{y}$ , I get

$$\overline{x} = \dfrac{m_x}{M} = \dfrac{\displaystyle \dint_R x \delta(x, y)\,dx\,dy}{\displaystyle \dint_R \delta(x, y)\,dx\,dy},$$

$$\overline{y} = \dfrac{m_y}{M} = \dfrac{\displaystyle \dint_R y \delta(x, y)\,dx\,dy}{\displaystyle \dint_R \delta(x, y)\,dx\,dy}.$$

We can do the same thing in 3 dimensions. Suppose a solid object occupies a region R in space, and that the density of the solid at the point $(x, y, z)$ is $\delta(x, y, z)$ . The total mass of the object is given by

$$M = \tint_R \delta(x, y, z)\,dx\,dy\,dz.$$

The moments in the x, y, and z directions are given by

$$m_x = \tint_R x \delta(x, y, z)\,dx\,dy\,dz,$$

$$m_y = \tint_R y \delta(x, y, z)\,dx\,dy\,dz,$$

$$m_z = \tint_R z \delta(x, y, z)\,dx\,dy\,dz.$$

You can think of them in a rough way as representing the "twisting" about the axis in question produced by a small bit of mass $\delta(x, y, z)\,dx\,dy\,dz$ at the point $(x, y, z)$ .

The center of mass is the point $(\overline{x}, \overline{y}, \overline{z})$ given by

$$\overline{x} = \dfrac{m_x}{M} = \dfrac{\displaystyle \tint_R x \delta(x, y, z)\,dx\,dy\,dz}{\displaystyle \tint_R \delta(x, y, z)\,dx\,dy\,dz},$$

$$\overline{y} = \dfrac{m_y}{M} = \dfrac{\displaystyle \tint_R y \delta(x, y, z)\,dx\,dy\,dz}{\displaystyle \tint_R \delta(x, y, z)\,dx\,dy\,dz},$$

$$\overline{z} = \dfrac{m_z}{M} = \dfrac{\displaystyle \tint_R z \delta(x, y, z)\,dx\,dy\,dz}{\displaystyle \tint_R \delta(x, y, z)\,dx\,dy\,dz}.$$

If a region in the plane or a solid in space has constant density $\delta(x, y, z) = k$ , then the center of mass is called the centroid. In this case, the density drops out of the formulas for $\overline{x}$ , $\overline{y}$ , and $\overline{z}$ . For example,

$$\overline{x} = \dfrac{\displaystyle \tint_R x \delta(x, y, z)\,dx\,dy\,dz}{\displaystyle \tint_R \delta(x, y, z)\,dx\,dy\,dz} = \dfrac{\displaystyle \tint_R x \cdot k\,dx\,dy\,dz}{\displaystyle \tint_R k\,dx\,dy\,dz} = \dfrac{\displaystyle \tint_R x\,dx\,dy\,dz}{\displaystyle \tint_R\,dx\,dy\,dz}.$$

(Of course, you can usually use a double integral to compute the volume of a solid.)

The centroid of the region is $(\overline{x}, \overline{y}, \overline{z})$ , where

$$\overline{x} = \dfrac{\displaystyle \tint_R x\,dx\,dy\,dz}{\displaystyle \tint_R\,dx\,dy\,dz}, \quad \overline{y} = \dfrac{\displaystyle \tint_R y\,dx\,dy\,dz}{\displaystyle \tint_R\,dx\,dy\,dz}, \quad \overline{z} = \dfrac{\displaystyle \tint_R z\,dx\,dy\,dz}{\displaystyle \tint_R\,dx\,dy\,dz}.$$

Recall that if R is a region in space, the volume of R is

$$V = \tint_R\,dx\,dy\,dz.$$

Thus, the denominators of the fractions above are all equal to volume of R.

The corresponding formulas for the centroid of a region in the plane are:

$$\overline{x} = \dfrac{\displaystyle \dint_R x\,dx\,dy}{\displaystyle \dint_R\,dx\,dy}, \quad \overline{y} = \dfrac{\displaystyle \dint_R y\,dx\,dy}{\displaystyle \dint_R\,dx\,dy}$$

Notice that the integral $\displaystyle \dint_R\,dx\,dy$ is just the area of R.

Example. Find the centroid of the region in the first quadrant bounded above by $y = x^2$ , from $x = 0$ to $x = 1$ .

$$\hbox{\epsfysize=1.5in \epsffile{center-of-mass-3.eps}}$$

Since the question is asking for the centroid, the density is assumed to be constant.

The region is

$$\left\{\matrix{ 0 \le x \le 1 \cr 0 \le y \le x^2 \cr}\right\}$$

First, the area is

$$\int_0^1 x^2\,dx = \left[\dfrac{1}{3} x^3\right]_0^1 = \dfrac{1}{3}.$$

Note that I didn't need a double integral to find the area.

The x-moment is

$$\int_0^1 \int_0^{x^2} x\,dx\,dx = \int_0^1 x \left[y\right]_0^{x^2}\,dx = \int_0^1 x^3\,dx = \left[\dfrac{1}{4} x^4\right]_0^1 = \dfrac{1}{4}.$$

The y-moment is

$$\int_0^1 \int_0^{x^2} y\,dx\,dx = \int_0^1 \left[\dfrac{1}{2} y^2\right]_0^{x^2}\,dx = \dfrac{1}{2} \int_0^1 x^4\,dx = \left[\dfrac{1}{10} x^5\right]_0^1 = \dfrac{1}{10}.$$

Therefore,

$$\overline{x} = \dfrac{\dfrac{1}{4}}{\dfrac{1}{3}} = \dfrac{3}{4}.$$

$$\overline{y} = \dfrac{\dfrac{1}{10}}{\dfrac{1}{3}} = \dfrac{3}{10}.$$

The centroid is $\left(\dfrac{3}{4}, \dfrac{3}{10}\right)$ .

You can often use symmetry to find the coordinates of the center of mass, or to determine a relationship among the coordinates --- for example, in some cases smmetry implies that some of the coordinates will be equal.

Example. Find the centroid of the region R bounded above by the plane $z = 4$ and below by the paraboloid $z = x^2 + y^2$ .

$$\hbox{\epsfysize=1.5in \epsffile{center-of-mass-4.eps}}$$

By symmetry, $\overline{x} = \overline{y} = 0$ , so I only need to find $\overline{z}$ . I'll use cylindrical coordinates.

$z = 4$ and $z = x^2 + y^2$ intersect in $x^2 + y^2 = 4$ , so the projection of R into the x-y-plane is the interior of the circle of radius 2 centered at the region.

Note that $z = x^2 + y^2 = r^2$ in cylindrical.

The region is

$$\left\{\matrix{ 0 \le \theta \le 2 \pi \cr 0 \le r \le 2 \cr r^2 \le z \le 4 \cr}\right\}$$

The volume is

$$\int_0^{2 \pi} \int_0^2 (4 - r^2) \cdot r\,dr\,d\theta = 2 \pi \int_0^2 (4 r - r^3)\,dr = 2 \pi \left[2 r^2 - \dfrac{1}{4} r^4\right]_0^2 = 8 \pi.$$

The z-moment is

$$\int_0^{2 \pi} \int_0^2 \int_{r^2}^4 z \cdot r\,dz\,dr\,d\theta = 2 \pi \int_0^2 r \left[\dfrac{1}{2} z^2\right]_{r^2}^4\,dr = 2 \pi \int_0^2 r \left(8 - \dfrac{1}{2} r^4\right)\,dr =$$

$$2 \pi \int_0^2 \left(8 r - \dfrac{1}{2} r^5\right)\,dr = 2 \pi \left[4 r^2 - \dfrac{1}{12} r^6\right]_0^2 = \dfrac{64 \pi}{3}.$$

Hence,

$$\overline{z} = \dfrac{\dfrac{64 \pi}{3}}{8 \pi} = \dfrac{8}{3}.$$

The centroid is $\left(0, 0, \dfrac{8}{3}\right)$ .

Example. Let R be the region in the first quadrant cut off by the line $x + y = 1$ . Suppose the region is made of a material with density $\delta(x, y) = 6 x + 6 y$ . Find the coordinates of the center of mass.

$$\hbox{\epsfysize=1.5in \epsffile{center-of-mass-5.eps}}$$

The region and the density are symmetric in x and y, so $\overline{x} = \overline{y}$ . I only need to find one of the coordinates.

The region is

$$\left\{\matrix{ 0 \le x \le 1 \cr 0 \le y \le 1 - x \cr}\right\}$$

The mass is

$$\int_0^1 \int_0^{1 - x} (6 x + 6 y)\,dy\,dx = \int_0^1 \left[6 x y + 3 y^2\right]_0^{1 - x}\,dx = \int_0^1 \left(6 x (1 - x) + 3 (1 - x)^2\right)\,dx =$$

$$\int_0^1 \left(6 x - 6 x^2 + 3 (1 - x)^2\right)\,dx = \left[3 x^2 - 2 x^3 - (1 - x)^3\right]_0^1 = 2.$$

The x-moment is

$$\int_0^1 \int_0^{1 - x} x (6 x + 6 y)\,dy\,dx = \int_0^1 \int_0^{1 - x} (6 x^2 + 6 x y)\,dy\,dx = \int_0^1 \left[6 x^2 y + 3 x y^2\right]_0^{1 - x}\,dx =$$

$$\int_0^1 \left(6 x^2 (1 - x) + 3 x (x - 1)^2\right)\,dx = \int_0^1 (3 x - 3 x^3)\,dx =$$

$$\left[\dfrac{3}{2} x^2 - \dfrac{3}{4} x^4\right]_0^1 = \dfrac{3}{4}.$$

Hence,

$$\overline{x} = \dfrac{\dfrac{3}{4}}{2} = \dfrac{3}{8}.$$

The center of mass is $\left(\dfrac{3}{8}, \dfrac{3}{8}\right)$ .

Example. Let R be the solid bounded below by $z = \sqrt{x^2 + y^2}$ and above by $z = \sqrt{4 - x^2 - y^2}$ , and assume that the density is $\delta(x, y, z) = z$ . Find the coordinates of the center of mass.

I'll convert to spherical coordinates. $z = \sqrt{x^2 + y^2}$ is a cone whose sides make an angle o $\dfrac{\pi}{4}$ with the positive z-axis. $z = \sqrt{4 - x^2 - y^2}$ is the top hemisphere of a sphere of radius 2 centered at the origin.

$$\hbox{\epsfysize=1.5 in \epsffile{center-of-mass-6.eps}}$$

The region is

$$\left\{\matrix{ 0 \le \theta \le 2 \pi \cr 0 \le \rho \le 2 \cr \noalign{\vskip2pt} 0 \le \phi \le \dfrac{\pi}{4} \cr}\right\}$$

Note that the density is

$$\delta = z = \rho \cos \phi.$$

Hence, the mass is

$$\int_0^{2 \pi} \int_0^2 \int_0^{\pi / 4} \rho \cos \phi \cdot \rho^2 \sin \phi\,d\phi\,d\rho\,d\theta = 2 \pi \int_0^2 \rho^3 \left[\dfrac{1}{2} (\sin \phi)^2\right]_0^{\pi /4}\,d\rho =$$

$$\pi \int_0^2 \rho^3\,d\rho = \pi \left[\dfrac{1}{4} \rho^4\right]_0^2 = 2 \pi.$$

(I did the $\phi$ integral using the substitution $u = \sin \phi$ .)

Since the region and the density are both symmetric about the z-axis, $\overline{x} = \overline{y} = 0$ . Therefore, I only need to find $\overline{z}$ .

Since $\delta = z = \rho \cos \phi$ , the z-moment is

$$\int_0^{2 \pi} \int_0^2 \int_0^{\pi / 4} \rho \cos \phi \cdot \rho \cos \phi \cdot \rho^2 \sin \phi\,d\phi\,d\rho\,d\theta = 2 \pi \int_0^2 \int_0^{\pi / 4} \rho^4 (\cos \phi)^2 \sin \phi\,d\phi\,d\rho =$$

$$2 \pi \int_0^2 \rho^4 \left[-\dfrac{1}{3} (\cos \phi)^3\right]_0^{\pi / 4}\,d\rho = \dfrac{2 \pi}{3} \left(1 - \dfrac{1}{2 \sqrt{2}}\right) \int_0^2 \rho^4\,d\rho =$$

$$\dfrac{2 \pi}{3} \left(1 - \dfrac{1}{2 \sqrt{2}}\right) \left[\dfrac{1}{5} \rho^5\right]_0^2 = \dfrac{64 \pi}{15} \left(1 - \dfrac{1}{2 \sqrt{2}}\right).$$

(I did the $\phi$ integral using the substitution $u = \cos \phi$ .)

Hence,

$$\overline{z} = \dfrac{\dfrac{64 \pi}{15} \left(1 - \dfrac{1}{2 \sqrt{2}}\right)}{2 \pi} = \dfrac{32}{15} \left(1 - \dfrac{1}{2 \sqrt{2}}\right).$$

The center of mass is $\left(0, 0, \dfrac{32}{15} \left(1 - \dfrac{1}{2 \sqrt{2}}\right)\right)$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga