The Chain Rule

Suppose $f: \real^p \rightarrow \real^n$ and $g: \real^n \rightarrow \real^m$ are functions of several variables, where the number of outputs of f equals the number of inputs of g. You can "chain" f and g together to make the composite function $g \circ f$ :

$$\matrix{ & f & & g & \cr \real^p & \rightarrow & \real^n & \rightarrow & \real^m \cr}$$

That is, $(g \circ f)(x) = g\left(f(x)\right)$ .

The derivative of $g \circ f$ is given by the Chain Rule. It is exactly what you'd expect, based on your experience with functions of one variable.

Theorem. Suppose $f: \real^p \to \real^n$ is differentiable at c, and $g: \real^n \to \real^m$ is differentiable at $f(c)$ . Then $g \circ f$ is differentiable at c, and

$$D(g \circ f)(c) = Dg[f(c)] \circ Df(c).\quad\halmos$$

In fact, $Dg$ can be represented by an $m \times n$ matrix, while $Df$ can be represented by an $n \times p$ matrix. The product on the right is the product of two matrices; it makes sense, because the n columns of $Dg$ are compatible with the n rows of $Df$ .

Example. Suppose

$$(x, y, z) = f(s, t) = (s^2 - t^2, s^2 + t^2, st), \quad (u, v) = g(x, y, z) = (2 x y - 3 y z, x z).$$

(a) Use the Chain Rule to compute $D(g\cdot f)(s, t)$ .

(b) Find $\pder u s$ and $\pder v s$ .

(a) Here is a picture which shows the dependencies of the variables:

$$\hbox{\epsfysize=1.755 in \epsffile{chain-rule-1.eps}}$$

For example, changing s causes x, y, and z to change, which in turn causes u and v to change.

First, compute $Df$ and $Dg$ :

$$Df = \left[\matrix{ 2 s & -2 t \cr 2 s & 2 t \cr t & s \cr}\right], \quad Dg = \left[\matrix{ 2 y & 2 x - 3 z & -3 y \cr z & 0 & x \cr}\right].$$

Next, multiply to obtain $D(g \circ f)(s, t)$ , being careful to put $Dg$ on the left:

$$D(g \circ f)(s, t) = \left[\matrix{ 2 y & 2 x - 3 z & -3 y \cr z & 0 & x \cr}\right] \left[\matrix{ 2 s & -2 t \cr 2 s & 2 t \cr t & s \cr}\right] = \left[\matrix{ 4 y s + 4 x s - 6 z s - 3 y t & -4 y t + 4 x t - 6 z t - 3 y s \cr 2 s z + x t & -2 z t + x s \cr}\right].$$

If you wish, you can substitute

$$x = s^2 - t^2, \quad y = s^2 + t^2, \quad z = s t.$$

This gives

$$D(g \circ f)(s, t) = \left[\matrix{ 8 s^3 - 9 s^2 t + 3 t^3 & -3 s^3 + 9 s t^2 - 8 t^3 \cr 3 s^2 t + t^3 & s^3 + 3 s t^2 \cr}\right].\quad\halmos$$

Note: This kind of substitution becomes messy when the functions are at all complicated, so I'll often leave the derivative as a product of matrices with "different variables",

(b) Here is how to interpret the matrix for $D(g \circ f)(s, t)$ . The composite function is $(u, v) = (g\cdot f)(s, t)$ . Therefore,

$$D(g \circ f)(s, t) = \left[\matrix{ \pder u s & \pder u t \cr \pder v s & \pder v t \cr}\right].$$

So, for example,

$$\pder v s = 3 s^2 t + t^3.$$

I'll check this directly.

$$v = x z = (s^2 + t^2)(s t) = s^3 t + s t^3, \quad\hbox{so}\quad \pder v s = 3 s^2 t + t^3.$$

Alternatively, if all you need is one of the partials (say $\pder u s$ ), you can use the variable dependency picture to get the formula. Consider all paths in the picture from u to s. Label each path with the corresponding partial derivative. For example, the path from u to y is labelled with $u_y = \pder u y$ .

$$\hbox{\epsfysize=1.75 in \epsffile{chain-rule-2.eps}}$$

Now to get $\pder u s$ , multiply along each path and add the results:

$$\pder u s = \pder u x \pder x s + \pder u y \pder y s + \pder u z \pder z s = (2 y)(2 s) + (2 x - 3 z)(2 s) + (-3 y)(t).\quad\halmos$$

Example. Suppose that $(x, y) = f(s, t)$ , $(u, v) = g(x, y)$ , $f(0, 1) = (2, -2)$ , and

$$\eqalign{ Df(0, 1) = \left[\matrix{ 1 & -1 \cr 0 & 2 \cr}\right], \quad & Df(2, -2) = \left[\matrix{ 3 & -3 \cr 2 & 0 \cr}\right],\cr Dg(0, 1) = \left[\matrix{ 2 & 1 \cr 1 & 2 \cr}\right], \quad & Dg(2, -2) = \left[\matrix{ 1 & 1 \cr 5 & -1 \cr}\right]. \cr}$$

Find $D(g \circ f)(0, 1)$ and $\left.\pder v s\right|_{(0, 1)}$ .

First,

$$D(g \circ f)(0, 1) = Dg\left(f(0, 1)\right) \circ Df(0, 1) = Dg(2, -2) \circ Df(0, 1) = \left[\matrix{1 & 1 \cr 5 & -1 \cr}\right] \left[\matrix{1 & -1 \cr 0 & 2 \cr}\right] = \left[\matrix{1 & 1 \cr 5 & -7 \cr}\right].$$

Now

$$D(g \circ f)(s, t) = \left[\matrix{ \pder u s & \pder u t \cr \pder v s & \pder v t \cr}\right].$$

It follows that $\left.\pder v s\right|_{(0, 1)} = 5$ .

Example. Suppose

$$w = 5 x^2 y - y^2 z + \ln z.$$

$$x = \cos 6 t, \quad y = \dfrac{2}{t} + 3, \quad z = e^{t^2}.$$

Find $\der w t$ .

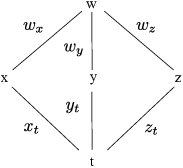
$$\hbox{\epsfysize=1.5in \epsffile{chain-rule-3.eps}}$$

$$\der w t = \pder w x \der x t + \pder w y \der y t + \pder w z \der z t = (10 x y)(-6 \sin 6 t) + (5 x^2 - 2 y z)\left(-\dfrac{2}{t^2}\right) + \left(-y^2 + \dfrac{1}{z}\right)(2 t e^{t^2}).\quad\halmos$$

Note: I'm leaving the answer in terms of x, y, z, and t. If you really needed everything in terms of t, you could substitute using the x, y, and z-equations.

Example. Suppose $(u, v) = f(x, y, z)$ and $(x, y, z) = g(s, t)$ are defined by

$$u = x^2 + y^2 + z^2, \quad v = 5 x y z,$$

$$x = \cos s \cos t, \quad y = \cos s \sin t, \quad z = \sin s.$$

Find $\pder u s$ and $\pder v t$ .

$$\hbox{\epsfysize=1.5in \epsffile{chain-rule-4.eps}}$$

$$\pder u s = \pder u x \pder x s + \pder u y \pder y s + \pder u z \pder z s = (2 x)(-\sin s \cos t) + (2 y)(-\sin s \sin t) + (2 z)(\cos s).$$

$$\pder v t = \pder v x \pder x t + \pder v y \pder y t + \pder v z \pder z t = (5 y z)(-\cos s \sin t) + (5 x z)(\cos s \cos t) + (5 x y)(0).\quad\halmos$$

Note: I'm leaving the answer in terms of x, y, z, s, and t. If you really needed everything in terms of s and t, you could substitute using the x, y, and z-equations.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga